Powers D.L. Boundary Value Problems and Partial Differential Equations

Подождите немного. Документ загружается.

78 Chapter 1 Fourier Series and Integrals

f (x ) =|x|+x, −1 < x < 1;

b. f (x) = x cos(x), −

< x <

;

c. f (x) = x cos(x), −1 < x < 1;

d. f (x) =



0, 1 < x < 3,

1, −1 < x < 1,

x, −3 < x < −1.

3. TowhatvaluedoestheFourierseriesoff converge if f is a continuous,

sectionally smooth, periodic function? Give an example.

4. State convergence theorems for the Fourier sine and cosine series that arise

from half-range expansions.

5. A function is given on the interval 0 < x < 2 by the formula

f (x) =



x, 0 < x < 1,

1 −x, 1 < x < 2.

a. Sketch the odd periodic extension

(x) for −4 < x < 4.

b. Explain why

(x) is sectionally smooth.

c. Determine the value that the sine series of f converges to at these points:

x = 1, x = 2, x = 9.6, x =−3.8.

6. For the same function given in Exercise 5, answer the same questions for

(x), the even periodic extension of f and its cosine series.

7. The series

∞



n=1

(−1)

cos(nx)

converges to a function f (x) whose formula on the interval −π<x <π is

f (x ) = A +Bx + Cx

Determine A, B,andC.

8. The series

∞



n=1

sin(nx)

converges to a continuous periodic function. On the interval 0 < x < 2π ,

this function coincides with a polynomial p(x) of degree 3. Find the polyno-

mial. Hint: Determine points x on the interval 0 < x < 2π where p(x) = 0.

Use this information to get a form for p(x).

1.4 Uniform Convergence 79

9. The function f (x) is periodic with period 2. Its graph for −1 < x < 1isa

semicircle with radius 1 centered at the origin.

a. Find the equation of f (x) for −1 < x < 1.

b. Determine the value of the coefﬁcient a

in its Fourier series. (This is the

only cosine coefﬁcient that can be found in closed form.)

c. Is f (x) sectionally smooth?

d. What does the theorem tell us about the convergence of the Fourier se-

ries of f (x)?

1.4 Uniform Convergence

The theorem of the preceding section treats convergence at individual points

of an interval. A stronger kind of convergence is uniform convergence in an

interval. Let

(x) = a



n=1

cos



nπx



sin



nπx



be the partial sum of the Fourier series of a function f .Themaximumdevia-

tion between the graphs of S

(x) and f (x) is

=max



f (x ) −S

(x)



, −a ≤x ≤ a,

where the maximum

is taken over all x in the interval, including the end-

points. If the maximum deviation tends to zero as N increases, we say that the

series converges uniformly in the interval −a ≤ x ≤ a.

Roughly speaking, if a Fourier series converges uniformly, then the sum of a

ﬁnite number N of terms gives a good approximation — to within ±δ

—of

the value of f (x) at any and every point of the interval. Furthermore, by taking

alargeenoughN, one can make the error as small as necessary.

There are two important facts about uniform convergence. If a Fourier series

converges uniformly in a period interval, then (1) it must converge to a con-

tinuous function, and (2) it must converge to the (continuous) function that

generates the series. Thus, a function that has a nonremovable discontinuity

cannot have a uniformly convergent Fourier series. (And not all continuous

functions have uniformly convergent Fourier series.)

Figure 9 presents graphs of some partial sums of a square-wave function. It

is easy to see that for every N there are points near x = 0andx =±π where

If f is not continuous, the maximum must be replaced by the supremum, or least upper

bound.

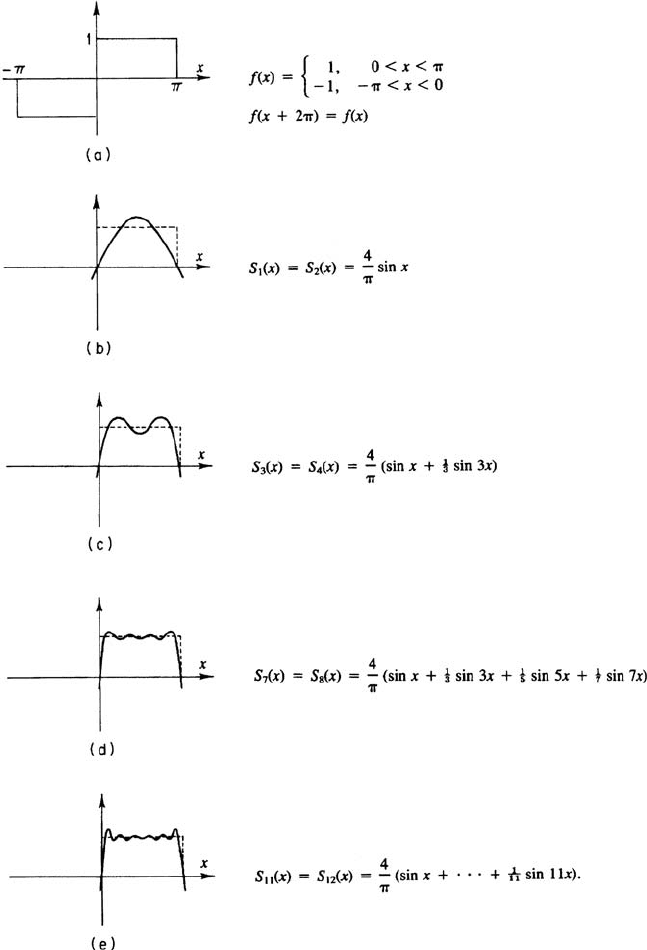
80 Chapter 1 Fourier Series and Integrals

Figure 9 Partial sums of the square-wave function. Convergence is not uniform.

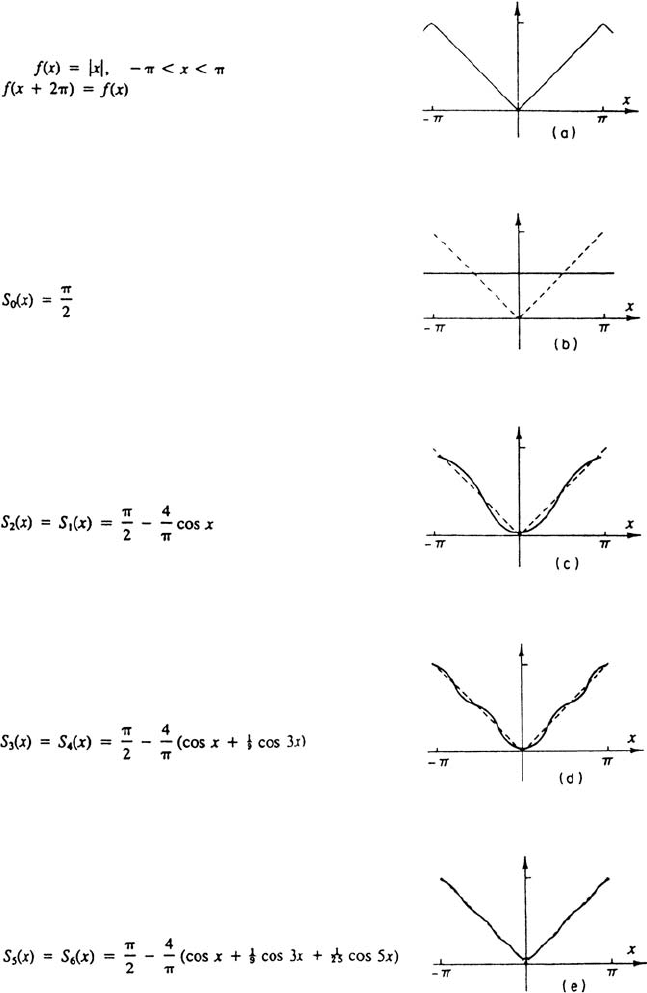
1.4 Uniform Convergence 81

Figure 10 Partial sums of a sawtooth function. Convergence is uniform.

82 Chapter 1 Fourier Series and Integrals

|f (x) − S

(x)| isnearlyequalto1,soconvergenceisnot uniform. (Inciden-

tally, the graphs in Fig. 9 also show the partial sums of f (x) overshooting their

mark near x = 0. This feature of Fourier series is called Gibbs’ phenomenon

and always occurs near a jump.) On the other hand, Fig. 10 shows graphs of a

“sawtooth” function and the partial sums of its Fourier series. The maximum

deviation always occurs at x = 0, and the convergence is uniform.

One of the ways of proving uniform convergence is by examining the coef-

ﬁcients.

Theorem 1. If the series



∞

n=1

(|a

|+|b

|) converges, then the Fourier seri es

∞



n=1

cos



nπx



sin



nπx



converges uniformly in the interval −a ≤x ≤ a and, in fact, on the whole interval

−∞< x < ∞.



Example.

For the function

f (x) =|x|, −π<x <π,

the Fourier coefﬁcients are

, a

cos(nπ)−1

, b

=0.

Since the series



∞

n=1

1/n

converges, the series of absolute values of the coefﬁ-

cients converges, and so the Fourier series converges uniformly on the interval

−π ≤ x ≤ π to |x|. The Fourier series converges uniformly to the periodic

extension of f (x) on the whole real line (see Fig. 10).



Another way of proving uniform convergence of a Fourier series is by exam-

ining the function f that generates it.

Theorem 2. If f i s periodic and continuous and has a sectionally continuous

derivative, then the Fourier series corresponding to f converges uniformly to f (x)

on the entire real axis.



While this theorem is stated for a periodic function, it may be adapted to a

function f (x) given on the interval −a < x < a.Iftheperiodic exte nsion of f

satisﬁes the conditions of the theorem, then the Fourier series of f converges

uniformly on the interval −a ≤ x ≤a.

Example.

Consider the function

f (x) = x, −1 < x < 1.

1.4 Uniform Convergence 83

Although f (x) is continuous and has a continuous derivative in the interval

−1 < x < 1, the periodic extension of f is not continuous. The Fourier series

cannot converge uniformly in any interval containing 1 or −1becausethepe-

riodic extension of f has jumps there, but uniform convergence must produce

acontinuousfunction.

On the other hand, the function f (x) =|sin(x)|, periodic with period 2π ,is

continuous and has a sectionally continuous derivative. Therefore, its Fourier

series converges uniformly to f (x) everywhere.



Here is a restatement of Theorem 2 for a function given on the interval

−a < x < a. The condition at the endpoints replaces the condition of conti-

nuity of the periodic extension of f .

Theorem 3. If f (x) is given on −a < x < a, if f is continuous and bounded and

has a sectionally continuous derivative, and if f (−a+) = f (a−), then the Fourier

series of f converges uniformly to f on the interval −a ≤ x ≤ a. (The series con-

verges to f (a−) = f (−a+) at x =±a.)



If an odd periodic function is to be continuous, it must have value 0 at x = 0

and at the endpoints of the symmetric period-interval. Thus, the odd periodic

extension of a function given in 0 < x < a may have jump discontinuities even

though it is continuous where originally given. The even periodic extension

causes no such difﬁculty, however.

Theorem 4. If f (x) is given on 0 < x < a, if f is continuous and bounded and has

a sectionally continuous derivative, and if f (0+) = f (a−) = 0, then the Fourier

sine series of f converges unifor mly to f in the interval 0 ≤ x ≤ a. (The series

converges to 0 at x = 0 and x =a.)



Theorem 5. If f (x) is given on 0 < x < a and if f is continuous and bounded

and has a sectionally continuous derivative, then the Fourier cosine series of f

convergesuniformlytof intheinterval0 ≤x ≤ a. (The series converges to f (0+)

at x = 0 and to f (a−) at x =a.)



EXERCISES

1. Determine whether the Fourier series of the following functions converge

uniformly or not. Sketch each function.

a. f (x) = e

, −1 < x < 1;

b. f (x) = sinh(x ), −π<x <π;

c. f (x) = sin(x), −π<x <π;

84 Chapter 1 Fourier Series and Integrals

f (x ) = sin(x) +|sin(x)|, −π<x <π;

e. f (x) = x +|x|, −π<x <π;

f. f (x) = x(x

−1), −1 < x < 1;

g. f (x) = 1 +2x −2x

, −1 < x < 1.

2. The Fourier series of the function

f (x ) =

sin(x)

, −π<x <π,

converges at every point. To what value does the series converge at x = 0?

at x =π ? The convergence is uniform. Why?

3. Determine whether the sine and cosine series of the following functions

converge uniformly. Sketch.

a. f (x) = sinh(x), 0 < x <π;

b. f (x) = sin(x ), 0 < x <π;

c. f (x) = sin(π x ), 0 < x <

;

d. f (x) = 1/(1 + x), 0 < x < 1;

e. f (x) = 1/(1 + x

), 0 < x < 2.

4. If a

and b

tend to zero as n tends to inﬁnity, show that the series

∞



n=1

−αn



cos(nx) + b

sin(nx)



converges uniformly (α > 0).

5. For each of the following coefﬁcients, use Theorem 1 to decide whether

convergence of the associate Fourier series is uniform.

a. a

sin

(nπ/2)

, b

=0;

b. a

=0, b

1 −cos(nπ)

nπ

;

c. a

=0, a

2(1 +cos(nπ))

−1

(n ≥2), b

=0;

d. a

=0, b

cosh(nπ/2)

1.5 Operations on Fourier Series 85

1.5 Operations on Fourier Series

In the course of this book we shall have to perform certain operations on

Fourier series. The purpose of this section is to ﬁnd conditions under which

they are legitimate. Two things must be noted, however. First, the theorems

stated here are not the best possible: There are theorems with weaker hypothe-

ses and the same conclusions. Second, in applying mathematics, we often carry

out operations formally, legitimate or not. The results must then be checked

for correctness.

Throughout this section we shall state results about functions and Fourier

series with period 2π , for typographic convenience. The results remain true

when the period is 2a instead. For functions deﬁned only on a ﬁnite interval,

the periodic extension must fulﬁll the hypotheses. We shall refer to a function

f (x) with the series shown:

f (x ) ∼ a

∞



n=1

cos(nx) + b

sin(nx). (1)

Theorem 1. The Fourier series of the function cf (x) has coefﬁcients ca

,ca

,and

(cisconstant).



This theorem is a simple consequence of the fact that a constant passes

through an integral. The fact that the integral of a sum is the sum of the inte-

grals leads to the following.

Theorem 2. The Fourier coefﬁcients of the sum f (x) + g(x) are the sums of the

corresponding c oefﬁcients of f (x) and g(x).



These two theorems are so natural that the reader has probably used them

already without thinking about it. The theorems that follow are much more

difﬁcult to prove, but they are extremely important.

Theorem 3. If f (x) is periodic and sectionally continuous, the n the Fourier series

of f may be integrated term by term:



f (x ) dx =



dx +

∞



n=1





cos(nx) + b

sin(nx)



dx. (2)



Theorem 4. If f (x) is periodic and sectionally continuous and if g(x) is sect ionally

continuous for a ≤x ≤ b, then

86 Chapter 1 Fourier Series and Integrals



f (x )g(x) dx =



g(x) dx

∞



n=1





cos(nx) + b

sin(nx)



g(x) dx. (3)



In Theorems 3 and 4, the function f (x) is only required to be sectionally

continuous. It is not necessary that the Fourier series of f (x) converge at all.

Nevertheless, the theorems guarantee that the series on the right converges and

equals the integral on the left in Eqs. (2) and (4).

One important application of Theorem 4 was the derivation of the formulas

for the Fourier coefﬁcients in Section 1. An application of Theorems 3 and 4

is given in what follows.

Example.

The periodic function g(x) whose formula in the interval 0 < x < 2π is

g(x) = x, 0 < x < 2π

has the Fourier series

g(x) ∼ π −2

∞



n=1

sin(nx)

By applying Theorems 1 and 2, we ﬁnd that the function f (x) deﬁned by f (x) =

[π −g(x)]/2 has the series

f (x) ∼

∞



n=1

sin(nx)

This manipulation would be simple algebra if the correspondence ∼ were an

equality.

The function f (x) satisﬁes the hypotheses of Theorem 3. Thus we may inte-

grate the preceding series from 0 to b to obtain



f (x) dx =

∞



n=1

1 −cos(nb)

Theorem 3 guarantees that this equality holds for any b.Intheintervalfrom0

to 2π we have the formula f (x) = (π −x)/2. Hence



f (x) dx =

πb

−

∞



n=1

1 −cos(nb)

, 0 ≤b ≤ 2π.

1.5 Operations on Fourier Series 87

Now, replacing b by x,wehave

x(2π −x)

∞



n=1

−

∞



n=1

cos(nx)

, 0 ≤x ≤ 2π. (4)

Outside the indicated interval, the periodic extension of the function on the

left equals the series on the right.

It is worthwhile to mention that the series on the right of Eq. (4) is the

Fourier series of the function on the left. That is to say,

2π



2π

x(2π −x)

dx =

∞



n=1

, (5)



2π

x(2π −x)

cos(nx) dx =

−1

, (6)



2π

x(2π −x)

sin(nx) dx = 0. (7)

Equations (6) and (7) can be veriﬁed directly, of course, but Theorem 4, to-

gether with the orthogonality relations of Section 1, also guarantees them. In

addition, Eq. (5) gives us a way to evaluate the series on the right.



Although the uniqueness property stated in the following theorem is so very

natural that we tend to assume it is true without checking, it really is a conse-

quence of Theorem 4.

Theorem 5. If f (x) is periodic and sectionally continuous, its Fourier series is

unique.



That is to say, only one series can correspond to f (x).Weoftenmakeuseof

uniqueness in this way: If two Fourier series are equal (or correspond to the

same function), then the coefﬁcients of like terms must match.

The last operation to be discussed is differentiation, one that plays a princi-

pal role in applications.

Theorem 6. If f (x ) is periodic, cont inuous, and sectionally smooth, then the dif-

ferentiated Fourier series of f (x) converges to f



(x) at every point x where f



(x)

exists:



(x) =

∞



n=1



−na

sin(nx) +nb

cos(nx)



. (8)



The hypotheses on f (x) itself imply (see Section 4) that the Fourier series of

f (x) converges uniformly. If f (x) (or its periodic extension) fails to be contin-