Potter T.D., Colman B.R. (co-chief editors). The handbook of weather, climate, and water: dynamics, climate physical meteorology, weather systems, and measurements

Подождите немного. Документ загружается.

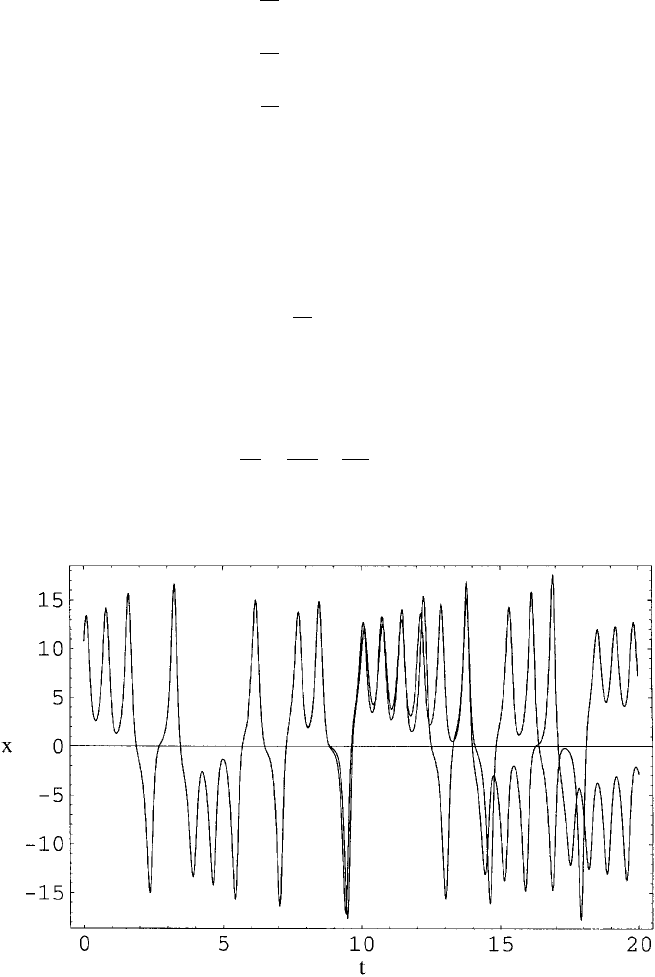
Sensitive dependence was ﬁrst discovered by Lorenz using the so-called Lorenz

equations:

¼ sðy  xÞ

¼xz þ rx  y

¼ xy  bz ð5Þ

Despite being only three dimensional, the Lorenz system and its variants continue to

be used in predictability studies. The Lorenz equations display sensitive dependence

on initial conditions (Fig. 1) and have a strange attractor (Fig. 2).

Sensitive dependence obviously has a signiﬁcant impact on predictability and is

quantiﬁed in terms of Lyapunov exponents, which are a generalization of the error

growth rate deﬁned in Eq. (4). Consider a nonlinear dynamical system

¼ FðyÞð6Þ

with a solution X(t). Consider an initially small perturbation to this trajectory, x (0),

which gives a new trajectory X

(t) ¼X(t) þ x(t). The difference, or error, x(t) evolves

via the linearization of the dynamical equations:



¼ FðX þ xÞFðXÞ

¼ MðXÞx ð7Þ

Figure 1 Two trajectories of the Lorenz equations with initial separation 0.00001.

PREDICTABILITY AND CHAOS

where the linearization of the dynamics at X is given by the matrix

ðXÞ¼

ðyÞ



y¼X

ð8Þ

and terms of O(x

) are ignored because the perturbation is assumed to be small.

The distance, or error, between the two trajectories is given by d ¼kxk where the

norm kk must be speciﬁed. The choice of norm is highly subjective and the appro-

priate choice depends on the situation. Some simple common nor ms are quadratic

functions of the state variables, such as the total energy or total enstrophy. However,

if your goal is to plan a picnic, then a local preci pitation norm would be more

appropriate.

Since Eq. (7) shows that the error growth is linear in the error we expect the error

to grow exponentially as in (3). However, due to the nonlinear nature of the

dynamics, when d becomes large enough that O(d

) O(d), the linearized equation

(7) breaks down. To follow error growth for long times requires either including

nonlinear terms in the error growth equation or shrinking the initial d as the predic-

tion time grows so that the ﬁnal error remains small. Including nonlinear effects

causes difﬁculty over long times since eventually the error grows to the size of the

attractor and then remains roughly constant. Averaging error growth over these long

times results in zero averaged error growth. A measure of the error growth over the

whole attractor thus requires making the initial error smaller as the time gets longer.

The result is the Lyapunov exponent l:

l ¼ lim

t!1

dð0Þ!0

dðtÞ

dð0Þ

ð9Þ

Figure 2 Lorenz attractor at b ¼

, s ¼10, and r ¼28.

1 NONLINEAR DYNAMICS AND CHAOS 87

The Lyapunov exponent is thus the mean exponential error growth rate linearized

about the true trajectory averaged over the entire attractor. If the Lyapunov exponent

is positive, errors grow, while if it is negative, errors decay.

For an n-dimensional dynamical system there are actually n Lyapunov exponents,

typically ordere d from largest to smallest. Over long times, the largest Lyapunov

exponent will dominate error growth and is given by Eq. (9). The spectrum of

Lyapunov exponents can be unders tood in terms of the propaga tor matrix G of

Eq. (7), deﬁned by:

xðtÞ¼Gðt; 0Þxð0Þð10Þ

For a quadratic norm, the error is given by:

kxk

¼hGðt; 0Þxð0Þ; Gðt; 0Þxð0Þi

¼hxð0Þ; Gðt; 0Þ

Gðt; 0Þxið11Þ

where G

{

is the adjoint of G with respect to the norm. The matrix G

{

G is some times

called the Oseledec matrix. The n eigenvalues s

and the n eigenvectors of G

{

G are

called the singular values and singular vectors, respectively, of G. The Lyapunov

exponents l

are related to the singular values by:

¼ lim

t!1

ln s

ð12Þ

Since chaotic systems have sensitive dependen ce on initial conditions, their

largest Lyapunov exponent must be positive. Positive largest Lyapunov exponents

impose a practical limit on predictability. While the Laplacian view is still valid in

that knowledge of the exact initial condition, x(0) ¼0, allows perfect prediction, any

small errors in the initial condition grow rapidly. Increasing the length of time a

forecast error is below some threshold requires decreasing the errors in the initial

condition. Since errors grow exponentially, the gain in prediction time is much

smaller than the associated decrease in initial error. In particular, decreasing the

initial error by a factor of e results in an increase in prediction time of only 1=l.

Cur rent estimates for the atmosphere indicate that the maximum practical prediction

time is about 2 weeks.

2 STOCHASTIC DYN AMICS

Although the atmosphere and other components of the climate system are funda-

mentally deterministic chaotic dynamical systems, they can often be considered as

random systems. Due to the high dimensionality of the atmosphere, there is a broad

range of space and time scales. If one is interested in the slower motion of the large

scales, then the faster variation of the small scales can be parameterized as random

noise. Loss of predictability in the resulting stochastic system is not due to the

88 PREDICTABILITY AND CHAOS

Lyapunov exponent of the deterministic part of the system, but rather to the lack of

predictability in the noise itself. Physically, however, since the noise is merely a

parameterization of fast processes with large Lyapunov exponents, it is the determi-

nistic chaos of the parameterized processes that ultimately is the cause of the loss of

predictability.

The simplest such system is a deterministic stable ﬁxed point per turbed by white

noise,

dxðtÞ

¼ AxðtÞþ

nnðtÞ; ð13Þ

where x represent the state of the system in terms of its deviation from a stable ﬁxed

point, A is the linear operator describing the deterministic dynamics, and

xx is multi-

variate Gaussian white noise. A stable ﬁxed point requires that all of the eigenvalues

of A be negative. In climatic applications, the ﬁxed point is usually taken to be the

mean state of the system and x represents the anoma ly. This kind of stochastic

system has been used to study a number of climatic systems including the El

Nin

o–Souther Oscillation (ENSO) and extratropical atmospheric dynamics.

One of the most interesting features of these systems is that they can amplify the

noise. As for the calcul ation of Lyapunov exponents, the growth of anomalies

d ¼kxk, is governed by Eq. (11). Now, however, the propagator G has both deter-

ministic and stochastic components. In most climatic applications the deterministic

dynamics is non-normal, i.e., AA

{

7 A

{

A 6¼0. In this case the eigenvectors of A are

not orthogonal. For normal systems, the stability of the ﬁxed point ensures that all

perturbation s decay to zero monotonically. Non-normality, however, allows the

nonorthogonal eigenvectors to interfere and transient perturbation growth is possi-

ble. For a given time interval t, the maximum growth ratio is the largest eigenvalue of

{

(t,0)G(t, 0), which is the largest singular value of G. The perturbation that grows

the most is the eigenvector of G

{

(t,0)G(t, 0) corresponding to this eigenvalue, which

is the corresponding singular vector of G.

One can treat a time-evolving state perturbed by noise in a similar fashion. The

deterministic dynamics is described by its linearization about the time-evolving

state, Eq. (7), which is perturbed by adding noise. The propagator now depends

on the time-evolving state, but the error growth is still determined by its singular

values and singular vectors.

3 ENSEMBLE FORECASTING

When producing a forecast, it is becoming more common to provide an estimate of

how correct the forecast is likely to be (Ehrendorfer, 1997). For a perfect model,

forecast errors are due only to initial condition errors. The Lyapunov exponents are

measures of error growth averaged over the entire attractor. However, the short-time

error growth can vary signiﬁcantly from one location on the attractor to another. This

variation is described by so-called local Lyapunov exponents. The distribution of

3 ENSEMBLE FORECASTING 89

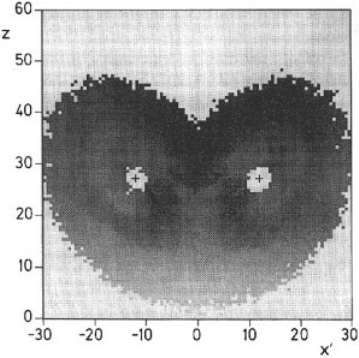
local Lyapunov exponents on the Lorenz attractor shows that the dynamics is least

predictable near the unstable ﬁxed point that divides the two lobes (Fig. 3). The

variation in local Lyapunov exponents indicates that some atmospheric states are

inherently more predictable than others.

An estimate of the believability of a forecast can be made by producing a large

number, or ensemble, of forecasts, each starting from a different initial condition,

where the ensemble of initial conditions is chosen to reﬂect the estimated distribu-

tion of initial condition errors. A forecast is more likely to be correct when the

resulting distribution of forecasts is narrow than when it is large. Furthermore, any

detailed structure in the distribution of forecasts indicates the type of forecast errors

likely to occur.

Due to the cost of making forecasts, and the high dimensionality of atmospheric

dynamics, it is impractical to use an ensemble large enough to adequately sample all

possible initial condition errors. Since many directions in phase space correspond to

stable directions, errors in these directions will decay and not affect the forecast

quality. Thus, a good estimate of forecast error can be obtained with a small ensem-

ble, provided the ensemble of initial conditions is distributed among the directions

responsible for the largest error growth.

Cur rently, there are two main techniques for producing such an ensemble in an

operational forecast: breeding methods and singular vectors. The European Center

for Medium-Range Weather Forecasting (ECMWF) ensemble prediction system

uses singular vectors, discussed above. The breeding method, used by National

Center for Environmental Prediction (NCEP), starts two initial conditions some

small distance apart and integrates them both using the fully nonlinear model result-

ing in a control solution and a perturbed solution. As the model evolves the two

Figure 3 Distribution of local Lyapunov exponents on the Lorenz attractor, with darker

(lighter) shadings indicating more (less) predictable regions (Eckhardt and Yao, 1993).

PREDICTABILITY AND CHAOS

solutions separate. After some time interval the difference between the control and

perturbation is rescaled back to its original amplitude and a new perturbed solution is

begun. After this cycle has been repeat ed several times, components of the perturba-

tion in stable and less unstable directions have been removed due to the rescalings.

The resulting bred modes are then used to initialize the ensemble.

Ensemble forecasts accurately represent forecast error only if the model itself is

accurate enough to approximately follow the true trajectory of the system. If the

model error is large, then the entire ensemble will evolve into a completely different

region in phase space than the true system. In this case, the ensemble spread is

irrelevant to the forecast error.

4 SEASONAL TO CLIMATE PREDICTABILITY

Predicting the atmosphere beyond the roughly 2-week limit of deterministic predict-

ability requires predicting its statistics rather than its actual state . Statistical predic-

tion is possible if there is some slow external forcing that signiﬁcantly affects the

structure of the attractor. Note that the division between internal and external varia-

bility is somewhat subjective. For example, in predicting the effect of ENSO on the

extratropics, the variation in tropical SST is considered an external forcing, while

when considering the climate response to increasing CO

, the behavior of tropical

SST is internal variability.

The land and ocean surface provide boundary conditions for the atmosphere and,

to the extent that they evolve slowly compared to the rapid dynamics of the weather,

they allow longer term prediction. For example, the variation of tropical SSTs asso-

ciated with ENSO evolves on a seasonal time scale. In addition, the relatively weak

nonlinearity in the tropical atmosphere–ocean system allows successful predictions

of ENSO well beyond the 2-week limit of extratropical weather. Thus, ENSO predic-

tion provides some degree of climate prediction. The degree to which the state of the

ENSO system affects the structure of the seasonal attractor can be seen in Figure 4,

which shows the effects of an El Nin

o episode on December–February climate.

One factor that can signiﬁcantly impact predictability is regime behavior, which

occurs when a system spends signiﬁcant amounts of time in localized regions of the

attractor, followed by relatively rapid transitions to other localized regions of the

attractor. For example, the two lobes of the Lorenz attractor in Figure 2 are regimes.

There is very little understanding of the generic regime behavior of high dimensional

chaotic attractors, and the role of regimes in intraseasonal to climate variability is

still a subject of debate despite decades of research.

Intraseasonal regimes have been described in a number of ways including varia-

tions in the Rossby wave amplitude, blocking events, and teleconnection patterns. It

has been suggested that the warming of the equatorial Paciﬁc in 1976, which

affected subsequent ENSO cycles, is an example of an interdecadal regime shift.

Climate events such as the Little Ice Age may indicate centennial-scale regimes and

glacial–interglacial transitions indicate regimes on even longer time scales.

4 SEASONAL TO CLIMATE PREDICTABILITY 91

Figure 4 Effect of an El Nin

o episode on December–February climate (courtesy Climate Prediction Center, NOAA).

Since weather statistics depend on the regime of the atmosphere, one avenue for

longer-term prediction is to focus on regime dynamics. Rather than predict the

speciﬁc evolution of the system trajectory, the goal is to predict the sequence of

regimes and their duration. Unfortunately, attempts at predicting the timing and

outcome of regime transitions have not been particularly successful.

Recently, Palmer (1999) has analyzed the predictability of climate under the

assumption that the climate attractor is composed of a number of dist inct quasi-

stationary regimes. Regimes are regions of the attractor that are relatively stable. For

example, the regimes in the Lorenz attractor are localized around unstable ﬁxed

points, which, despite being unstable, have stable subspaces that attract trajectories.

In the context of stochastic systems, the regimes may be modeled as truly stable

attractors and the transitions are then solely due to the random noise. The areas of

phase space between the regimes, the ‘‘saddles,’’ are more unstable, and the system

passes through these areas relatively quickly. An important feature of such saddles is

that they show sensitive dependence: The relationship between the speciﬁc location

where the system crosses the saddle and the regime it next visits can have fractal

structure. Palmer noted that smal l-amplitude forcing will affect this ﬁne-scale struc-

ture of the saddle much more than the relatively stable regime structure. The stability

of the behavior of the attractor to external forcing is called structural stability. Thus,

small-amplitude forcing will not change the str ucture of the regimes, i.e., they are

structurally relatively stable, but will affect the relative probability of the system

visiting a regime, which is structurally unstable. In the context of anthropogenic CO

increase, the resulting climate change will not show new climate regimes but, rather,

a shift in the occurrence of existing regimes. Thus, the fact that recent climate

changes are similar to naturally occurring variations does not disprove the possibility

that the changes have an anthropogenic cause.

REFERENCES

Eckhardt, B., and D. Yao (1993). Local Lyapunov exponents in chaotic systems, Physica D 65,

100–108.

ECMWF (1996). Predictability, Proceedings of a seminar held at ECMWF on predictability:

4–8 September 1995 Reading, European Centre for Medium-Range Weather Forecasts.

Ehrendorfer, M. (1997). Predicting the uncertainty of numerical weather forecasts: a review,

Meteorol. Z. 6, 147–183.

Laplace, P. S. (1825). Philosophical Essay on Probabilities, translated from the ﬁfth French

edition of 1825 by A. I. Dale, New York, Springer, 1995.

Lichtenberg, A. J., and M. A. Lieberman (1992). Regular and Chaotic Dynamics, New York,

Springer.

Lorenz, E. N. (1975). Climatic predictability, in The Physical Basis of Climate and Climate

Modelling, GARP Publication Series, (ICSU=WMO, Geneva), Vol. 16, pp. 132–136.

NATO (1996). Decadal Climate Variability: Dynamics and Predictability, Proceedings of the

NATO Advanced Study Institute held at Les Houches, France, February 13–24, 1995,

L. T. Anderson and J. Willebrand (eds.), Berlin, Springer.

Palmer, T. N. (1999). A nonlinear dynamical perspective on climate prediction, J. Climate 12,

575–591.

REFERENCES 93

CHAPTER 8

HISTORICAL OVERVIEW OF

NUMERICAL WEATHER PREDICTION

EUGENIA KALNAY

1 INTRODUCTION

In general, the public is not aware that our daily weather forecasts start out as initial-

value problems on the major National Weather Service supercomputers. Numerical

weather prediction provides the basic guidance for weather forecasting beyond the

ﬁrst few hours. For example, in the United States, computer weather forecasts issued

by the National Centers for Environmental Prediction (NCEP) in Washington, DC,

guide forecasts from the U.S. National Weather Service (NWS). NCEP forecasts are

performed running (integrating in time) computer models of the atmosphere that can

simulate, given today’s weather observations, the evolution of the atmosphere in the

next few days. Because the time integration of an atmospheric model is an initial-

value problem, the ability to make a skillful forecast requires both that the computer

model be a realistic representation of the atmosphere and that the initial conditions

be accurate. In what follows we will give examples of the evolution of numerical

weather prediction at NCEP, but they are representative of what has taken place in all

major international operational weather centers such as the European Centre for

Medium Range Weather Forecasts (ECMWF), the United Kingdom Meteorological

Ofﬁce (UKMO), and the weather services of Japan, Canada, and Australia.

Formerly the National Meteorological Center (NMC), the NCEP has performed

operational computer weather forecasts since the 1950s. From 1955 to 1973, the

forecasts included only the Northern Hemisphere; they have been global since 1973.

Over the years, the quality of the models and methods for using atmospheric

observations has improved continuously, resulting in major forecast improvements.

Handbook of Weather, Climate, and Water: Dynamics, Climate, Physical Meteorology, Weather Systems,

and Measurements, Edited by Thomas D. Potter and Bradley R. Colman.

ISBN 0-471-21490-6 # 2003 John Wiley & Sons, Inc.