Poole Ch.P., Jr. Handbook of Superconductivity

546 Chapter 11: Electrical Properties

References

A. Barone and G. Paterno,

Physics and Applications of the Josephson Effect.

Wiley. New York, 1982.

K. K. Likharev,

Dynamics of Josephson Junctions and Circuits.

Gordon and Breach, New York, 1986.

C. P. Poole, Jr., H. A. Farach, and R. J. Creswick,

Superconductivity.

Academic Press, New York, 1995.

T. van Duzer and C. W. Turner,

Principles of Superconductive Devices and Circuits.

Elsevier, New

York, 1981.

Chapter 12

Magnetic Properties

Charles P. Poole, Jr.

Department of Physics and Institute of Superconductivity,

University of South Carolina, Columbia, South Carolina

A. Introduction 547

B. Internal Fields and Magnetization 548

C. Critical Fields 550

D. Vortices 553

E. Vortex Anisotropies 554

E Individual Vortex Motion 556

G. Transport Current in a Magnetic Field 559

H. Magnetic Phase Diagram 560

I. Ellipsoids in Magnetic Fields 561

J. Intermediate State of Type I Superconductor

K. Ac Susceptibility 566

References 567

A

562

Introduction

One of the main characteristics of a superconductor is its magnetic behavior, and

this behavior arises from its vortex structure. The present chapter surveys the

configurations and interactions of vortices and discusses the macroscopic

magnetic properties that result from them. The role that they play in influencing

electric current flow and their dependence on the sample shape are examined.

Most of the chapter is devoted to Type II superconductivity, but toward the end

the intermediate state of a Type I superconductor is treated.

ISBN: 0-12-561460-8 HANDBOOK OF SUPERCONDUCTIVITY

$30.00 Copyright 9 2000 by Academic Press.

All fights of reproduction in any form reserved.

547

548

Chapter 12: Magnetic Properties

Internal Fields and Magnetization

The general expressions for the B and H fields,

B - #o(H + M) - ttH - #oH(1 + Z),

(1)

are valid both inside and outside a superconducting sample. Here M is the

magnetization or magnetic moment per unit volume, Z is the dimensionless

magnetic susceptibility, #0 is the permeability of free space where M- 0 and

g = 0, and #- #0(1 + Z) is the permeability of a medium. When an external

magnetic field Bap p = Happ/#0 is applied, the magnetization M = 0 in the free

space outside the sample. Inside the B and H fields are related to the magnetiza-

tion M through Eq. (1), so we have

Bin - #0Hin( 1 q- Z), (2)

where the dimensionless susceptibility Z

Z -- M/Hin

(3)

is an intrinsic property of the medium. If the medium is anisotropic, then the

susceptibility will have different values, Za, gb, and gc, along the three principal

directions, with Za

= ~b ~

Xc for axial symmetry.

For an ideal Type I superconductor Z -- -1, and assuming that there are no

demagnetization effects, we have the formulae

Bin

- 0

M -- -Hin

-- --Bapp//A0,

(4)

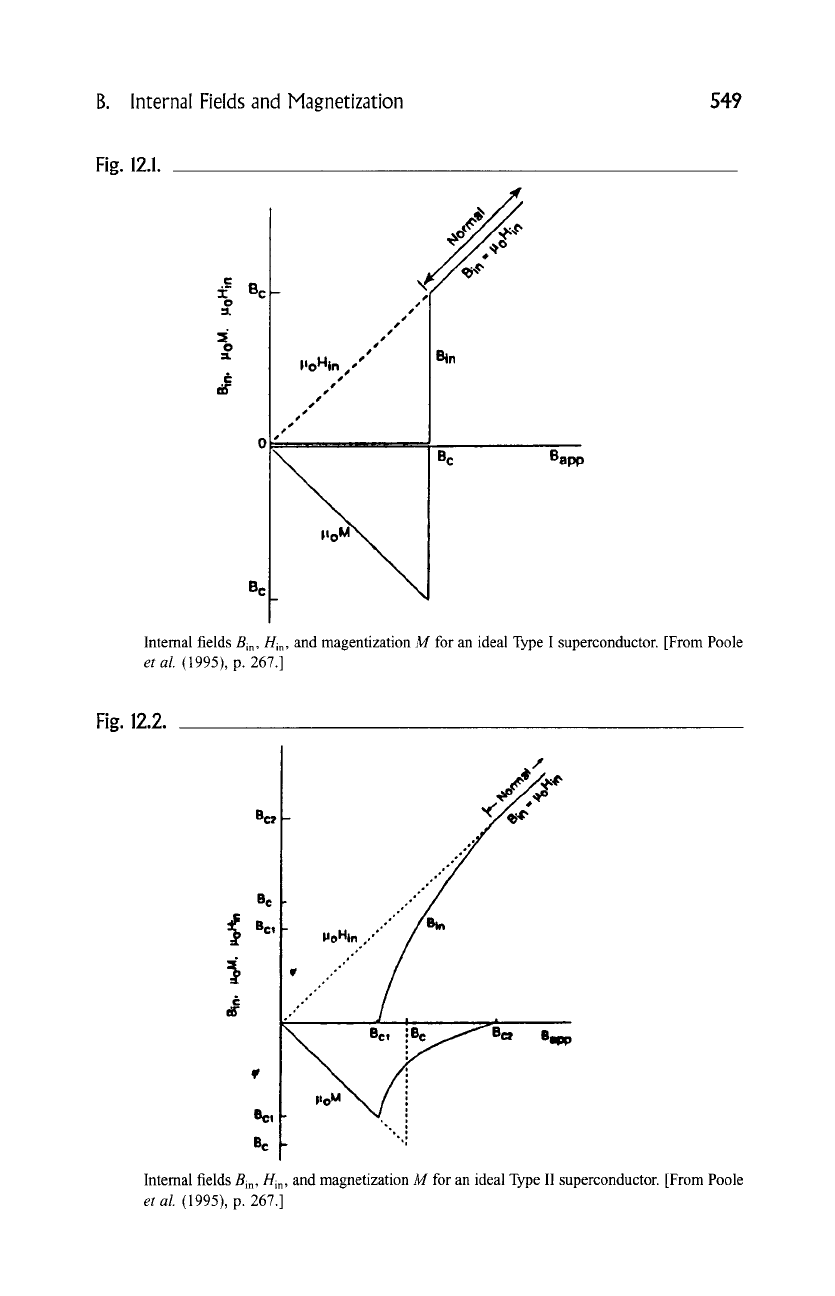
which are plotted in Fig. 12.1. For a Type II superconductor, which has two

critical fields Bcl and Bc2 , the analogous expressions have the form

Bin - 0

0 < Bap p < Bcl

M -- -/-/in -- -Bapp/#0

(5a)

Bcl < Bap p < Bc2

#0 M

_ _(Bapp _ Bin);

(5b)

shown plotted in Fig. 12.2. In practice the actual magnetization and intemal field

curves are more rounded than indicated by the figure.

Also shown in these two figures is the thermodynamic critical field

B c , defined geometrically for a Type II material by the equal area criterion

corresponding to the integrals

I•c

[Bc2

(Bapp "~- #0M)dBapp - #0 (-M)dBapp,

(6)

cl dBc

B. Internal Fields and Magnetization S47

Fig.

12.1.

C

•

B c

0

=1.

O

Iff

s

t

lloHln,, oS

I

t

O' ......

Bc

Bc Bapp

Intemal fields Bin , Bin , and magentization M for an ideal Type I superconductor. [From Poole

et al.

(1995), p. 267.]

Fig. 12.2.

f

x" *

Bc~ -

..o...'"'"

Br .

..""

~

...~

Be.

Internal fields Bin ,/-/in, and magnetization M for an ideal Type II superconductor. [From Poole

et al.

(1995), p. 267.]

550

Chapter

12:

Magnetic Properties

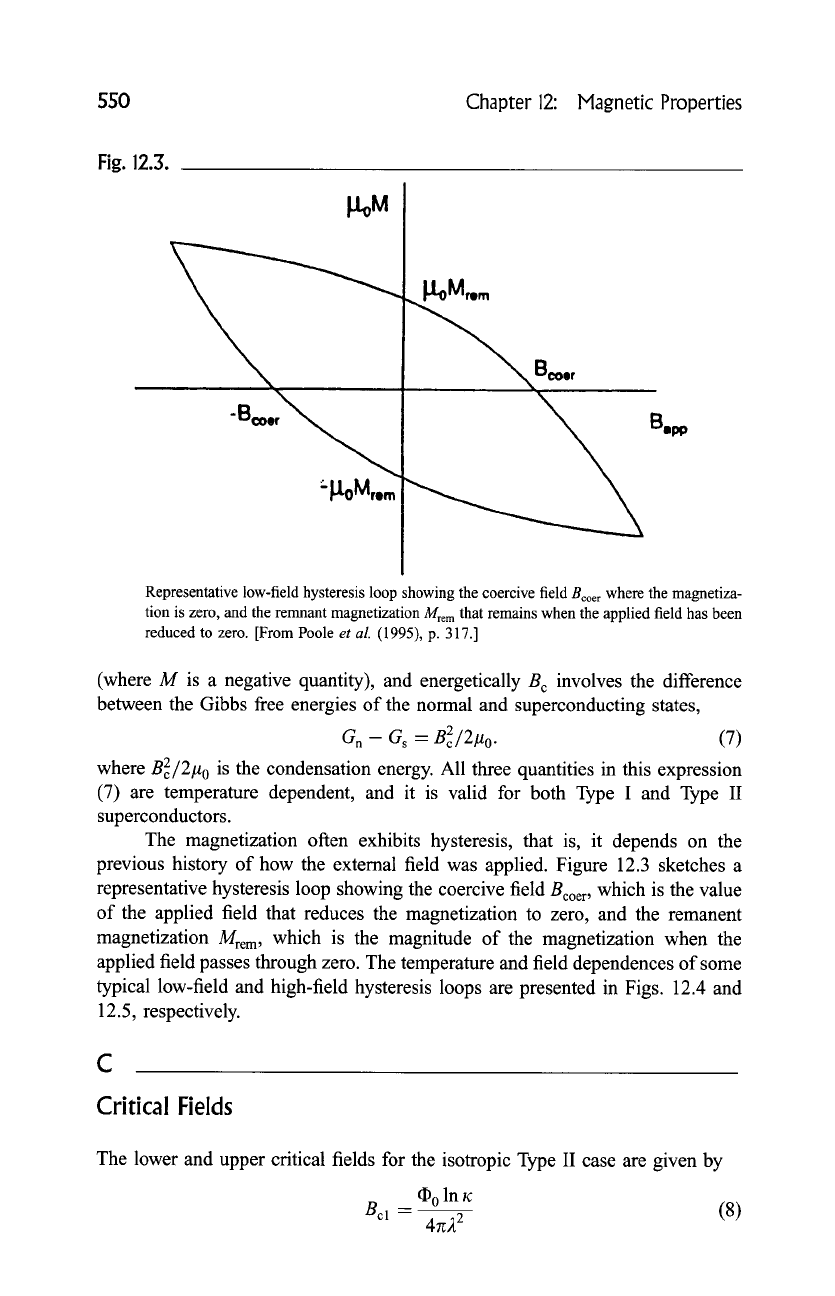
Fig. 12.3.

"Boo,,

Bco,r

~'J.l.0Mmm

Representative low-field hysteresis loop showing the coercive field Bcoer where the magnetiza-

tion is zero, and the remnant magnetization

Mre m

that remains when the applied field has been

reduced to zero. [From Poole

et al.

(1995), p. 317.]

(where M is a negative quantity), and energetically B c involves the difference

between the Gibbs free energies of the normal and superconducting states,

G n

--

G s --

B2/2~o .

(7)

where

B2/2#o

is the condensation energy. All three quantities in this expression

(7) are temperature dependent, and it is valid for both Type I and Type II

superconductors.

The magnetization often exhibits hysteresis, that is, it depends on the

previous history of how the external field was applied. Figure 12.3 sketches a

representative hysteresis loop showing the coercive field Bcoer, which is the value

of the applied field that reduces the magnetization to zero, and the remanent

magnetization Mrem, which is the magnitude of the magnetization when the

applied field passes through zero. The temperature and field dependences of some

typical low-field and high-field hysteresis loops are presented in Figs. 12.4 and

12.5, respectively.

C

Critical Fields

The lower and upper critical fields for the isotropic Type II case are given by

~o InK

Bcl -- (8)

47~ 2

C. Critical Fields 551

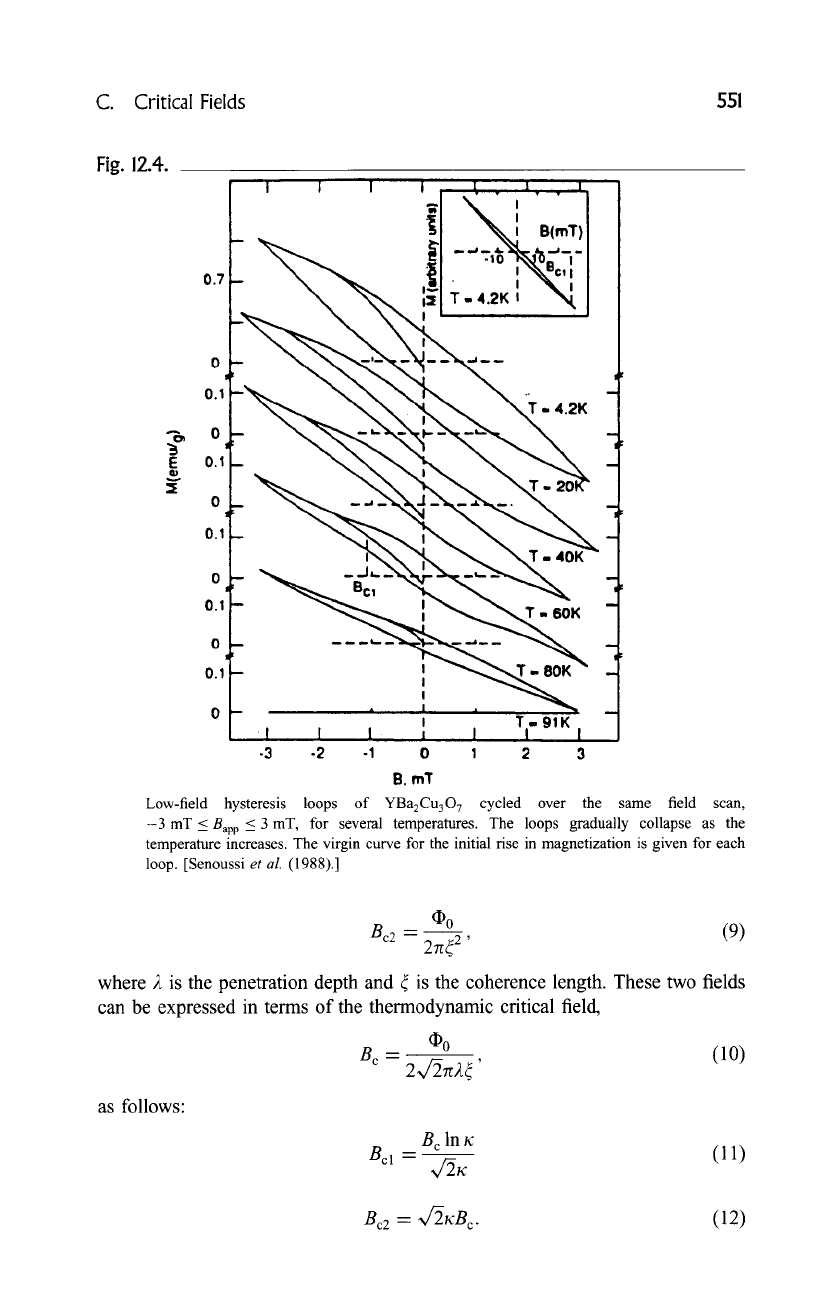
Fig. 12.4.

0.7

~1 B(mT)

.,o

N.o,',

9 I I

0.1

9 "~ 0

E 0.1

G)

v

0

T - 4.2K

0.1

0_

0.0 -I,,- ~~T.60K

o,j

,

0

........... -

I "I" ,, gIK

-3 -2 -1 0 1 2 3

B. mT

Low-field hysteresis loops of YBa2Cu307 cycled over the same field scan,

-3 mT < Bap p < 3 mT, for several temperatures. The loops gradually collapse as the

temperature increases. The virgin curve for the initial rise in magnetization is given for each

loop. [Senoussi

et al.

(1988).]

(I) o

Bc2 = 2~z~2,

(9)

where 2 is the penetration depth and ~ is the coherence length. These two fields

can be expressed in terms of the thermodynamic critical field,

(I)~ (10)

Be 2~/2rt2~ '

as follows:

B c

InK

Bcl -- %/~K (11)

Bc2 - ~/2trB c. (12)

552

Chapter 12: Magnetic Properties

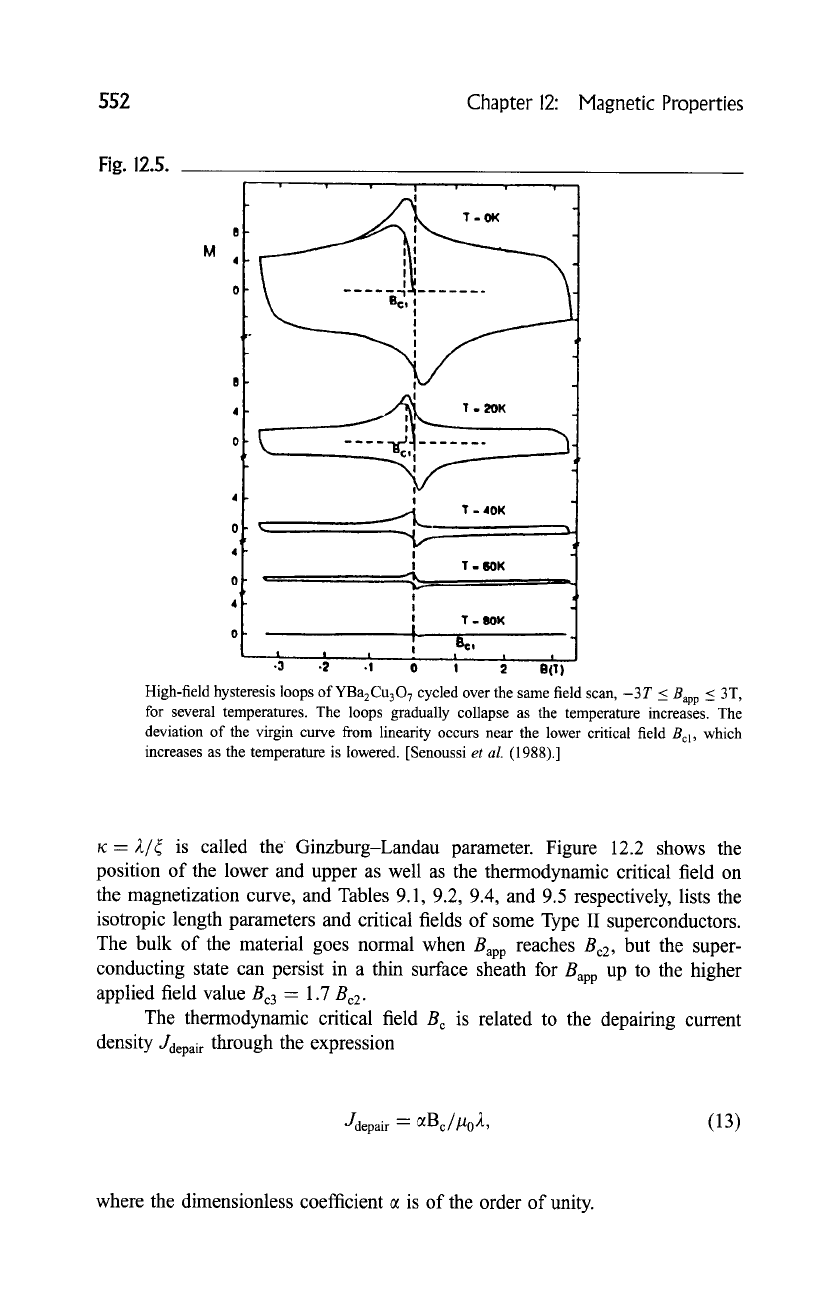
Fig. 12.5.

I'

I

Bcs I

I

T=~

0

4-

0

4 ~

0

4'

0

iv .i

!

X,.. ~, ~~,... T - 40K

9 ''~L

9 ~

""

I T - (X)K

_ _. , ~, 9 . 9

,,

i T 80K

9 , _ ,

;3' .~ .', o , ~ B(~)

High-field hysteresis loops ofYBa2Cu307 cycled over the same field scan, -3T _< Bap p _ 3T,

for several temperatures. The loops gradually collapse as the temperature increases. The

deviation of the virgin curve from linearity occurs near the lower critical field Bcl , which

increases as the temperature is lowered. [Senoussi

et al.

(1988).]

tr 2/~ is called the Ginzburg-Landau parameter. Figure 12.2 shows the

position of the lower and upper as well as the thermodynamic critical field on

the magnetization curve, and Tables 9.1, 9.2, 9.4, and 9.5 respectively, lists the

isotropic length parameters and critical fields of some Type II superconductors.

The bulk of the material goes normal when Bap p reaches Bc2 , but the super-

conducting state can persist in a thin surface sheath for Bap p up to the higher

applied field value Be3 = 1.7 Bc2.

The thermodynamic critical field B~ is related to the depairing current

density

Jdepair

through the expression

Jdepair --

~Bc/#02, (13)

where the dimensionless coefficient ~ is of the order of unity.

D. Vortices 553

D

Vortices

The magnetic flux of an individual (isolated) vortex is determined by integrating

its magnetic field over its area,

I

B.dA-~ o, (14)

and it equals the flux quantum ~0,

~o = h/2e

= 2.0678 • 10 -15 Tm 2.

(15)

This flux quantum ~0 is associated with the Hall effect quantum of resistance R H,

RI_ I = h/e 2

= 2~0/e = 25,813~.

(16)

Some superconductivity researchers use R 0 =

h/4e 2

= 6.45 Kf~ as the quantum

of resistance since the charge of a Cooper pair is 2e.

For the high ~c limit of the cuprates, 2 >> {, the vortex magnetic field

B(r)

and shielding current density Js(r) outside the core, r > ~, have the radial

dependences

B(r) - Oo~ Ko(r/2 )

(17)

27z~, 2

(I) 0

Js(r) --

KI(F/,~),

(18)

2~Z/~o/~ 3

where

Ko(r/2 )

and

Kl(r/~, )

are the zero-order and first-order modified Bessel

functions, respectively, with the properties that Kl(r ) >>

Ko(r )

for small r << 2,

and K 1 (r) ~

Ko(r )

for large r >> 2. Inside the core, r _< ~, we have Js(r) = 0, and

B(r)

may be approximated as having the constant value

(I) 0

B(r) --

7----7~ K0(~/2). (19)

2~zZ"

Equations (17) and (18) have the following asymptotic behaviors near the core:

(I) 0

B(r)-

z--zv.~ ln(1.1232/r), r << 2 (20)

2~zZ"

~o 2/r, r

<< 2, (21)

Js(r) - 2rc#0~3

554 Chapter 12: Magnetic Properties

Fig. 12.6.

0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0

Hexagonal vortex lattice. [From Poole

et al.

(1995), p. 277.]

and far away from the core

9 0 exp(-r/2)

B(r)

--

2(2~)1/2)~ 2

(r/~)l/2 ,

r >> 2 (22)

~o exp(-r/2)

Js(r) 2(2rc)1/2#023

(r/2) 1/2'

r >> 2. (23)

where the numerical factor 1.123 in Eq. (20) is 2e-~ and 7 = 0.57721566... is

the dimensionless Euler-Mascheroni constant.

Ordinarily, vortices arrange themselves in the hexadic pattern of Fig. 12.6

separated by the distance d, where 1 ~/~d 2 is the area occupied per vortex. Near

the lower critical field d ~ 22 and near the upper critical field d ~ 2~. For large tr

the amount of flux Ocore in the core of an isolated vortex is much less than the flux

quantum 9 0. Near the upper critical field Bc2 the vortex cores almost overlap and

the flux in each core approaches ~0. The average field Bin inside the super-

conductor is given by

(I) 0

Bin = 1 C'~d 2 = NA~O' (24)

2

where N A is the number of vortices per unit area.

Vortex Anisotropies

The characteristic length relationship of anisotropic superconductors is

~a2a -- ~b2b -- ~c/~c,

and the GL parameter/s in the/th principal direction is

12j2kl 1/2

Ki = 1/2"

Ir162

(25)

(26)

E. Vortex Anisotropies 555

The critical fields for the ith direction are obtained by generalizing Eqs. (11) and

(12), respectively:

In gi

Bcl --

~/~giBc

(27)

Bc2 --

~/-2giBc .

(28)

Comparing Eqs. (10) and (25), we see that the thermodynamic critical field,

O0

B e 2~/~rc~i2i

(29)

is independent of the direction.

Axially symmetric superconductors with in-plane (m*- m~') and axial

direction (m*) effective masses are characterized by the anisotropy ratio F,

F 2 9 9

-- me/mat, -- (~ab/~c) 2 -- (2c/2ab) 2,

(30)

where for the cuprates m* >

ma" ~

and we have

~c << ~ab << 2ab << 2c" (31)

Some reported values of these quantities are listed in Table 9.2. For the

cuprates with the applied field in the

ab

plane (gab) and along the c direction (gc),

respectively, we have

[2ab2cl 1/2

gab = iCabr

(32)

gc -- ~ab/~ab,

(33)

and Eqs. (27)-(29) provide the critical fields for axial symmetry in the

ab

plane,

O0 In gab

Bcl(ab)

= ~ (34)

4 7r, }Cab /~ c

Oo

Bcz(ab) - 2rC~ab~c

(35)

and along the c direction,

9 0 In

K c

Bcl(C) -- 4rC22a b (36)

Bc2(C)_ (I)0 .

2rc~Za b (37)

Table 9.5 provides some experimentally determined values of these critical field

anisotropies.

Poole Ch.P., Jr. Handbook of Superconductivity

Подождите немного. Документ загружается.