Poole Ch.P., Jr. Handbook of Superconductivity

Подождите немного. Документ загружается.

516

Chapter 10: Thermal Properties

Fig. 10.16.

(a)

--- 6-

"7 //

',x" " I/

=L 4- f

! -

ffl /

2- d j

1 "

~ ' I' i '" ! ' " I I"

100

200 300

(K)

Thermopower (crosses) of the Chevrel-phase superconductor Cul.gMo6S 5 Te 3. The solid line is

a fit to the theoretical expression for the electron-phonon mass enhancement. [After Kaiser

(1987).]

Perhaps the most striking feature of the thermopower in HTS is its strong

dependence on doping, that is, on the hole concentration in CuO 2 planes, and its

close tie with the doping trend in the transition temperature T c. The super-

conducting domain of HTS cuprates is delineated by the minimum, Pmin, and

maximum, Pmax, hole concentrations per planar Cu atom. Outside of these limits

there is no superconductivity. The overdoped samples (p --+ Pmax) have reduced

T c, a metallic character, and a substantially linear and negative thermopower. As

the hole density decreases (by means of nonisovalent substitutions or by lowering

the amount of oxygen), one achieves a certain optimal level of doping, which

yields the highest T c and for which the thermopower is small, with a room-

temperature value of practically zero. With a further decrease in the hole density

(P --+ Pmin), in the so-called underdoped domain, the T c decreases rapidly and the

thermopower attains larger positive values, but with a temperature dependence

that is essentially unchanged. Thus, as the material is brought from the overdoped

to the underdoped regime, the thermopower undergoes a steady shift upward and

toward more positive values. The slope of the thermopower, -3 • 10 -8 V/K 2, is

approximately the same for all cuprates, except the yttrium compound YBCO, 1

l In the text and in Tables 10.4 and 10.5 we use the following usual designations for the various

families of high-temperature superconductors: YBCO stands for YBa2Cu3OT_6, BSCCO represents

Bi2Sr2Ca., 1CunO2.+4, TBCCO designates TlmBa2Ca._ 1Cu.O2(.+l)+m, LSCO represents

La2_xSrxCuO4, and NCCO stands for Nd2_xCexCuO 4.

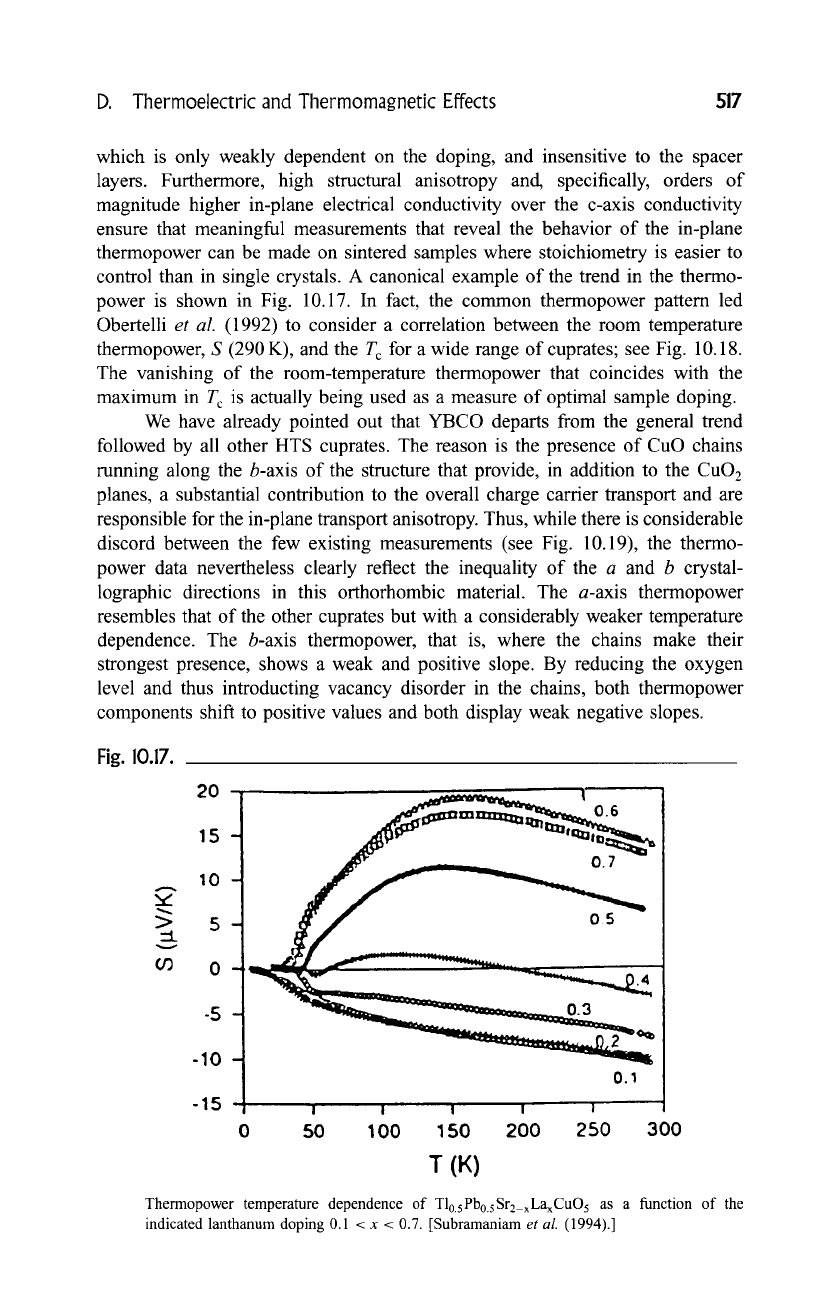
D. Thermoelectric and Thermomagnetic Effects 517

which is only weakly dependent on the doping, and insensitive to the spacer

layers. Furthermore, high structural anisotropy and, specifically, orders of

magnitude higher in-plane electrical conductivity over the c-axis conductivity

ensure that meaningful measurements that reveal the behavior of the in-plane

thermopower can be made on sintered samples where stoichiometry is easier to

control than in single crystals. A canonical example of the trend in the thermo-

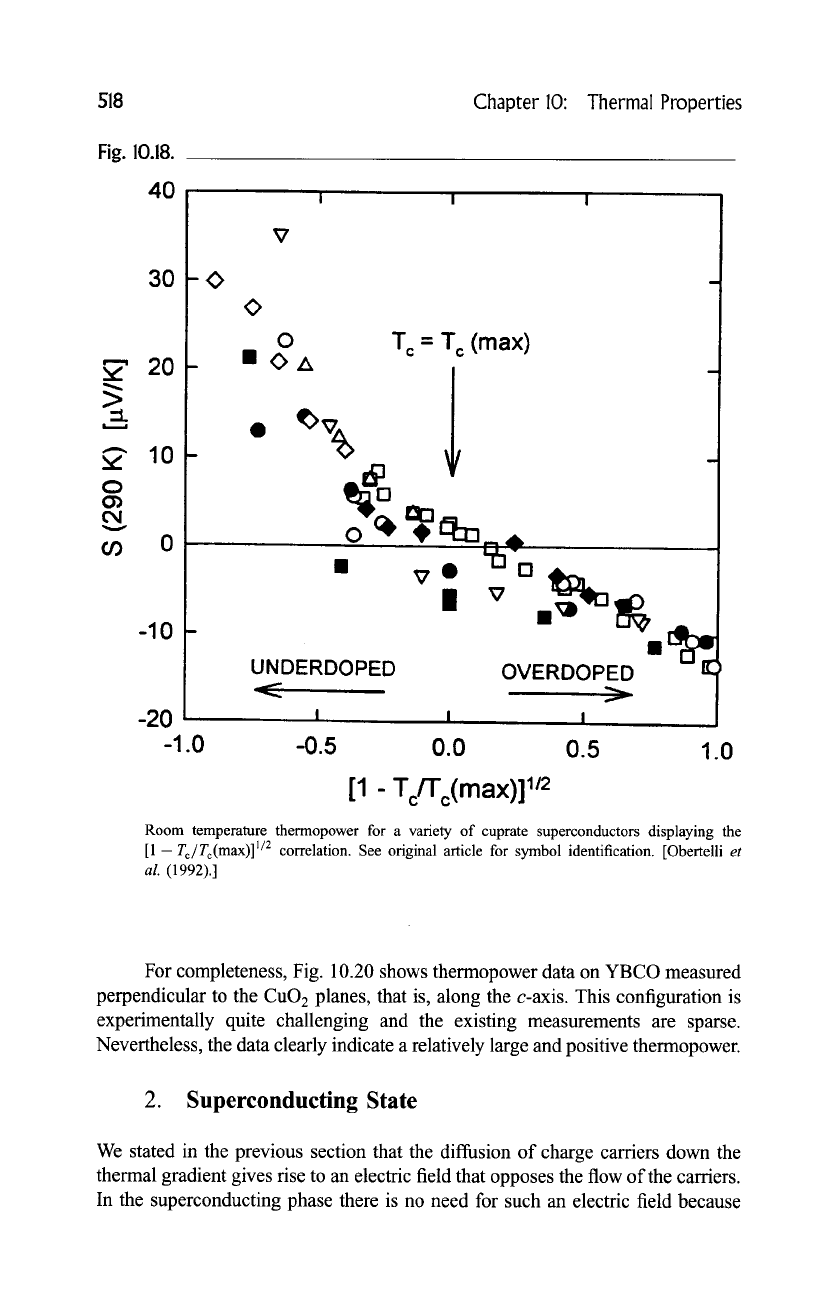
power is shown in Fig. 10.17. In fact, the common thermopower pattern led

Obertelli

et al.

(1992) to consider a correlation between the room temperature

thermopower, S (290 K), and the T c for a wide range of cuprates; see Fig. 10.18.

The vanishing of the room-temperature thermopower that coincides with the

maximum in T c is actually being used as a measure of optimal sample doping.

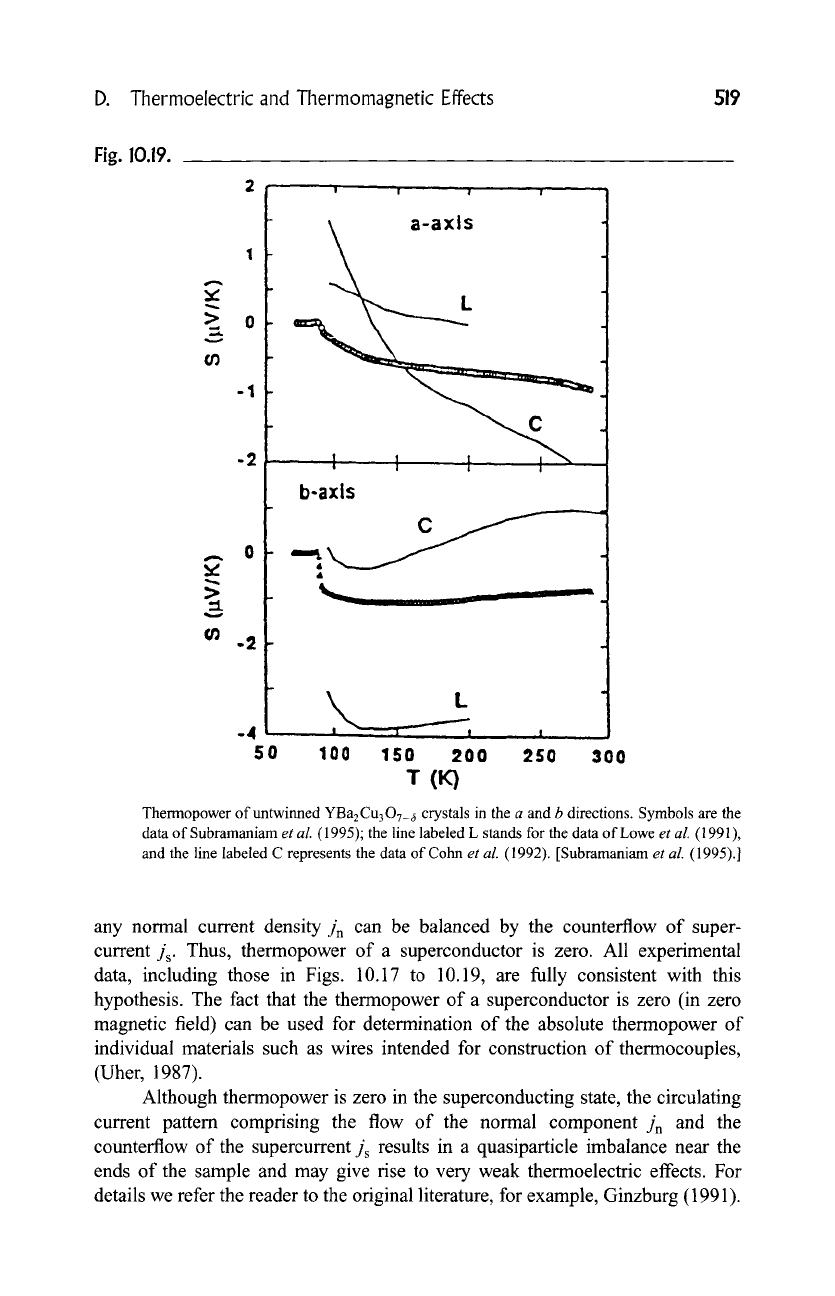
We have already pointed out that YBCO departs from the general trend

followed by all other HTS cuprates. The reason is the presence of CuO chains

running along the b-axis of the structure that provide, in addition to the CuO 2

planes, a substantial contribution to the overall charge carrier transport and are

responsible for the in-plane transport anisotropy. Thus, while there is considerable

discord between the few existing measurements (see Fig. 10.19), the thermo-

power data nevertheless clearly reflect the inequality of the a and b crystal-

lographic directions in this orthorhombic material. The a-axis thermopower

resembles that of the other cuprates but with a considerably weaker temperature

dependence. The b-axis thermopower, that is, where the chains make their

strongest presence, shows a weak and positive slope. By reducing the oxygen

level and thus introducting vacancy disorder in the chains, both thermopower

components shift to positive values and both display weak negative slopes.

Fig. 10.17.

:::t.

0.6

0.7

-5

-10

0 50

0.3

0.1

I ...... I I l a

1 O0 150 200 250 300

T (K)

Thermopower temperature dependence of T10.sPb0.sSrz_xLaxCuO 5 as a function of the

indicated lanthanum doping 0.1 < x < 0.7. [Subramaniam

et al.

(1994).]

518 Chapter 10: Thermal Properties

Fig. 10.18.

-<>

IlOA

-10 -

-20

-1.0

= T (max)

mc c

l v

UNDERDOPED OVERDOPED

, I I ..... I

-0.5 0.0 0.5 1.0

[1 - Tc/Tc(max)]lt2

Room temperature thermopower for a variety of cuprate superconductors displaying the

[1-

To~To(max)] ]/2

correlation. See original article for symbol identification. [Obertelli

al.

(1992).]

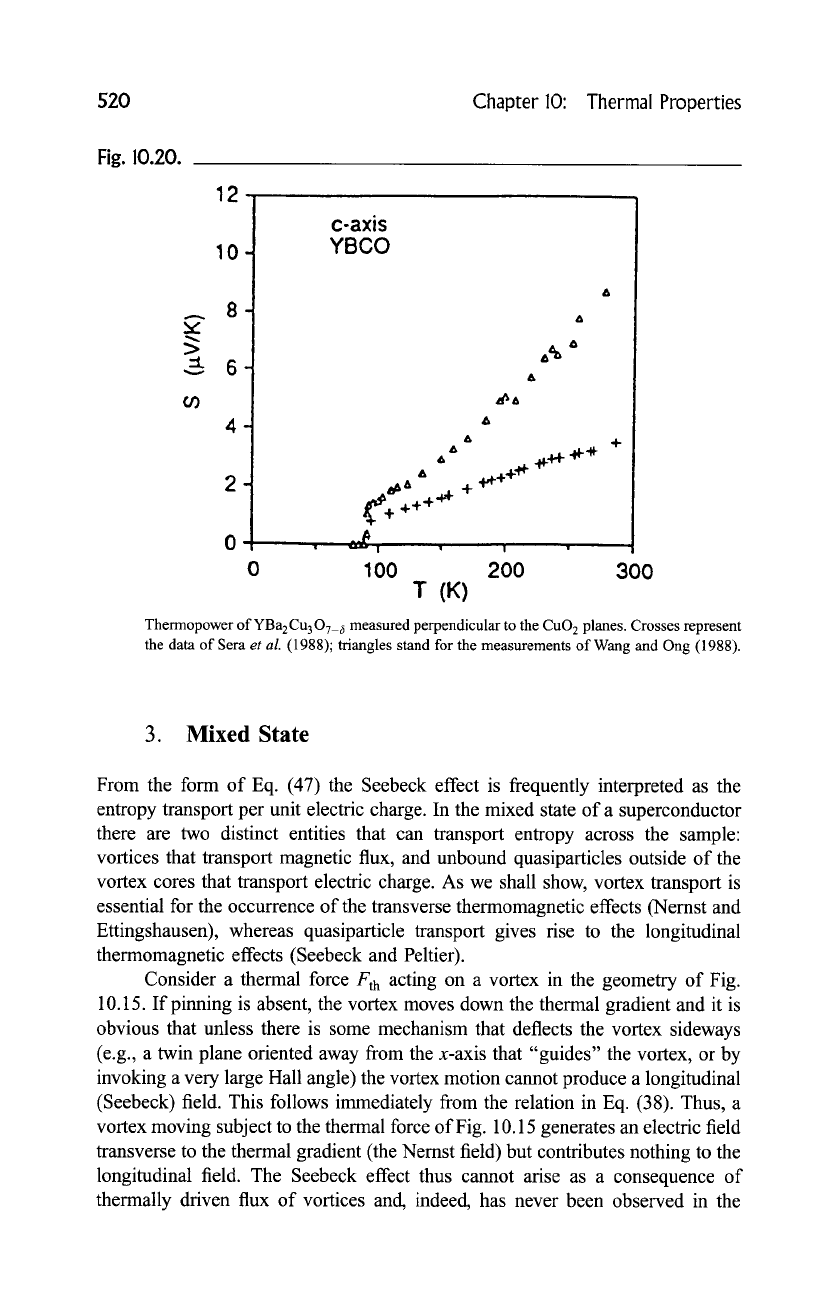
For completeness, Fig. 10.20 shows thermopower data on YBCO measured

perpendicular to the CuO 2 planes, that is, along the c-axis. This configuration is

experimentally quite challenging and the existing measurements are sparse.

Nevertheless, the data clearly indicate a relatively large and positive thermopower.

2. Superconducting State

We stated in the previous section that the diffusion of charge carriers down the

thermal gradient gives rise to an electric field that opposes the flow of the carriers.

In the superconducting phase there is no need for such an electric field because

D. Thermoelectric and Thermomagnetic Effects 519

Fig. 10.19.

> o

-1

-2

::t.

u~ -2

-- I '

' I ....... 1 .... ][

......

I I I ~'x "

b-axls

- .

-4 ' L "

_ 1, L__

50 100 150 200 2S0 300

(1<)

Thermopower of untwinned

YBa2Cu307_ 6

crystals in the a and b directions. Symbols are the

data of Subramaniam

et al.

(1995); the line labeled L stands for the data of Lowe

et al.

(1991),

and the line labeled C represents the data of Cohn

et al.

(1992). [Subramaniam

et al.

(1995).]

any normal current density Jn can be balanced by the counterflow of super-

current Js. Thus, thermopower of a superconductor is zero. All experimental

data, including those in Figs. 10.17 to 10.19, are fully consistent with this

hypothesis. The fact that the thermopower of a superconductor is zero (in zero

magnetic field) can be used for determination of the absolute thermopower of

individual materials such as wires intended for construction of thermocouples,

(Uher, 1987).

Although thermopower is zero in the superconducting state, the circulating

current pattern comprising the flow of the normal component Jn and the

counterflow of the supercurrent Js results in a quasiparticle imbalance near the

ends of the sample and may give rise to very weak thermoelectric effects. For

details we refer the reader to the original literature, for example, Ginzburg (1991).

520 Chapter 10: Thermal Properties

Fig. 10.20.

12-

10-

c-axis

YBCO

a6A

+ +++++

an~

+ -P~'++~ ~-H- ~ "~

100 200 300

(K)

Thermopower of YBa2Cu 3

07_ 6

measured perpendicular to the

CuO 2

planes. Crosses represent

the data of Sera

et al.

(1988); triangles stand for the measurements of Wang and Ong (1988).

3. Mixed State

From the form of Eq. (47) the Seebeck effect is frequently interpreted as the

entropy transport per unit electric charge. In the mixed state of a superconductor

there are two distinct entities that can transport entropy across the sample:

vortices that transport magnetic flux, and unbound quasiparticles outside of the

vortex cores that transport electric charge. As we shall show, vortex transport is

essential for the occurrence of the transverse thermomagnetic effects (Nernst and

Ettingshausen), whereas quasiparticle transport gives rise to the longitudinal

thermomagnetic effects (Seebeck and Peltier).

Consider a thermal force Fth acting on a vortex in the geometry of Fig.

10.15. If pinning is absent, the vortex moves down the thermal gradient and it is

obvious that unless there is some mechanism that deflects the vortex sideways

(e.g., a twin plane oriented away from the x-axis that "guides" the vortex, or by

invoking a very large Hall angle) the vortex motion cannot produce a longitudinal

(Seebeck) field. This follows immediately from the relation in Eq. (38). Thus, a

vortex moving subject to the thermal force of Fig. 10.15 generates an electric field

transverse to the thermal gradient (the Nernst field) but contributes nothing to the

longitudinal field. The Seebeck effect thus cannot arise as a consequence of

thermally driven flux of vortices and, indeed, has never been observed in the

D. Thermoelectric and Thermomagnetic Effects

521

conventional superconductors. In HTS cuprates, thanks to a fortuitous confluence

of a large region of reversibility and a power-law rather than exponential

dependence of the quasiparticle density that ensures the presence of quasiparti-

cles at temperatures well below Tc, the Seebeck effect is robust, can easily be

measured, and rivals the transverse thermomagnetic effects. The Seebeck effect in

this case stems from the quasiparticle transport or, more precisely, from

quasiparticles interacting with vortices.

A physical interpretation was first proposed by Huebener

et al.

(1990) and

subsequently refined by a number of authors (e.g., Ri

et aL,

1993; Meilikhov and

Farzetdinova, 1994). The essential physics is an extension of the two-fluid

counterflow model of Ginzburg to a regime where B r 0. Taking into account

Hall angles of both vortices (0v) and quasiparticles (0qp), the Seebeck effect for

the mixed state of a superconductor is

S = Sn(pf/pn)[1 -t-

tan 0 v tan 0qp] +

(S4)pf/d/)o)tan 0 v,

(48)

where

and

are the normal-state Seebeck coefficient and resistivity, and pf is

the flux flow resistivity. Later, we shall recognize the second term of Eq. (48) as

related to the Nemst coefficient multiplied by the tangent of the Hall angle.

If the sample contains any extended structural defects that could serve as

"guide rails" and guide the motion of vortices under angle q~ away from the

direction of-Vx T, Ghamlouch and Aubin (1996) have shown that Eq. (48)

becomes

S = Sn(pf/pn){[1 +

tan 0 v tan 0qp cos (p] +

(S4)pf/dPo)[tan

0 v + tan q~]} cos q0.

(49)

Since both Hall angles are typically very small, the dominant term in Eqs. (48)

and (49) is the first term and to a good approximation

S = Sn(pf/pn).

(50)

The Seebeck coefficient (thermopower) in the mixed state is thus closely related

to the flux-flow resistivity, Eq. (42). Just as the flux-flow resistivity reflects the

anisotropy of the structure (broader transition range for more anisotropic

materials), so does the Seebeck coefficient: More two-dimensional cuprates

have a more extended temperature range where the Seebeck effect is finite

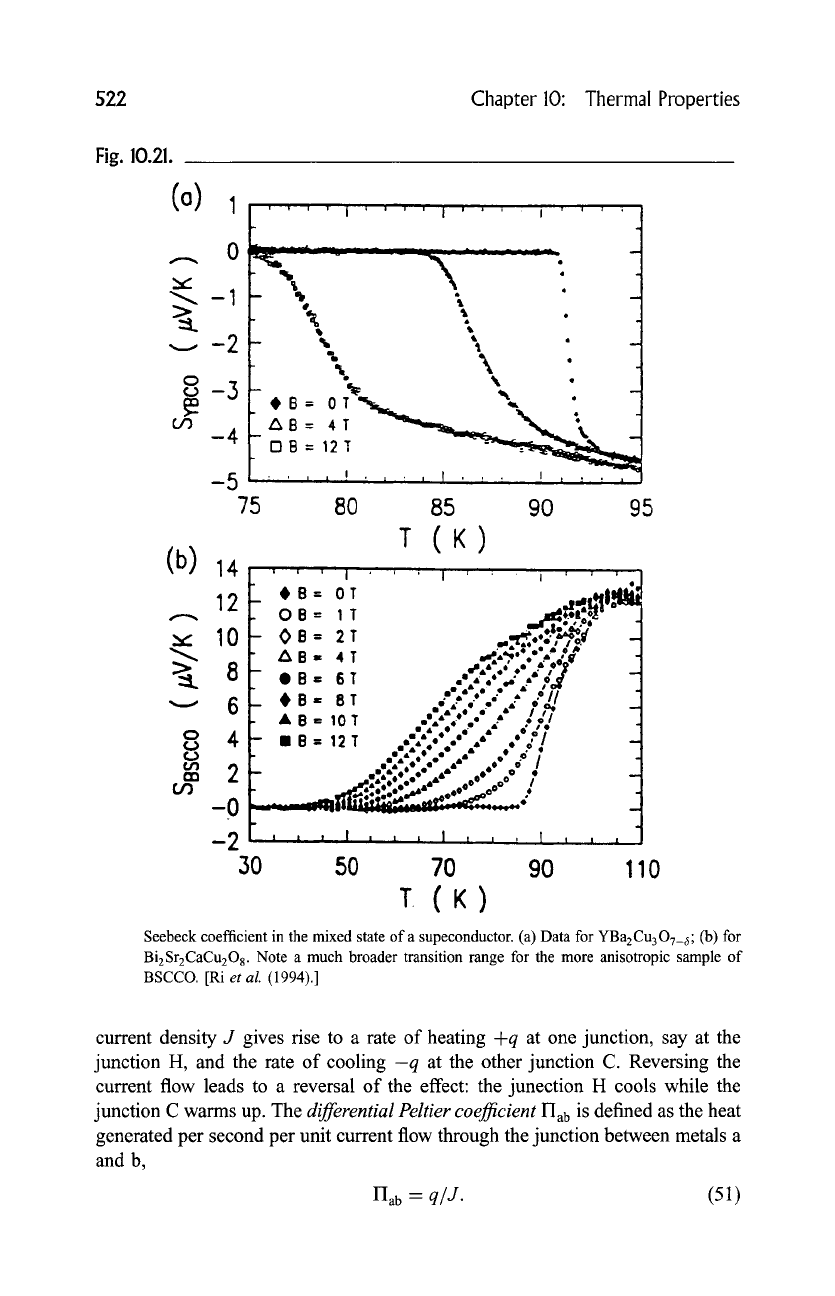
(compare Figs. 10.21 a and 10.21 b).

d. Peltier Effect

The Peltier effect arises as a consequence of the heat current density being carried

by the electric current density along an applied electric field in zero temperature

gradient. Assume that a battery is applied to the terminals A and B to drive a

current clockwise around the circuit consisting of a thermocouple (elements a and

b initially at the same temperature) as shown in Fig. 10.22. The presence of the

522

Chapter

10:

Thermal Properties

Fig. 10.21.

,,~ '~ ~ . "

~-I

- ,b ~

-2 ~ ~ ~ " -

9 . \ 9 .

o-3-

"~ ,,

. -

)O= 0T ,.

9

LIB= 41"

c/~ -4 -OB= 12T

-5

'''' '! ' ' .... ) ' ; ' J ....

75 80 85 90 95

T (K)

(b) 14 ,, ,", ...,,, ,.....,,, ........ ,,

)

o T

a.,,.~l~

o B = 1 T j~.l'~'

OB=

..;r#..., ,o: -

9 9 em_.A e~

A B ,, 4 T ,~.,-?9 9 ..-,,g,e "

~A .- .---

9 I l " &

' ,~ll

- ,e= 8T .'~," ," "','~ 9 -

9 e -- ~0 T .'.':".'"

/,"7 -

8 4 - - "'"" " ":/

16- 12T

.-.,,*.-" ." .*.,.

9 9 _e 9 - 9 ~ _

9 .'Z,*'.-" .," .o~ ,," I

-2 : ' ' ' I ' ' ' I , , , ,

....

30 50 70 90 110

T,(K)

Seebeck coefficient in the mixed state of a supeconductor. (a) Data for YBa2Cu307_~; (b) for

Bi2Sr2CaCu208. Note a much broader transition range for the more anisotropic sample of

BSCCO. [Ri

et al.

(1994).]

current density J gives rise to a rate of heating +q at one junction, say at the

junction H, and the rate of cooling -q at the other junction C. Reversing the

current flow leads to a reversal of the effect: the junection H cools while the

junction C warms up. The

differential Peltier coefficient

Hab is defined as the heat

generated per second per unit current flow through the junction between metals a

and b,

IIab

q/J.

(51)

D. Thermoelectric and Thermomagnetic Effects 52.3

Fig.

10.22.

+q -q

A B

Origin of the Peltier effect in a circuit consisting of two dissimilar semiconductors.

By convention, liab is taken as positive if the clockwise current in Fig. 10.22

makes the junction H warm and the junction C cold. Although the Peltier effect

can be observed only when one joins together dissimilar conductors (the same is

true for the Seebeck effect where the measuring probes play the role of the second

conductor), the effect is a bulk one and one can write the differential Peltier

coefficient as

lIab • lia -- lib,

(52)

where

l-I a

and

II b are

the

absolute Peltier coefficients

of the two individual

materials comprising the thermocouple. From now on we drop the subscripts and

will consider the Peltier coefficient of a single conductor.

Although the Peltier effect is the essence of thermoelectric refrigeration

(e.g., Goldsmid, 1986), the effect itself is rarely measured directly even in the

thermoelectric materials. Rather, one makes use of the Kelvin relation

n = rs, (53)

which allows determination of the Peltier coefficient knowing the behavior of the

Seebeck coefficient S and the absolute temperature T. Equation (53) in conjunc-

tion with any one of Eqs. (48)-(50) allows the Peltier coefficient to be assessed in

the mixed state of a superconductor. For example, the dominant contribution to

the Seebeck coefficient, Eq. (50), immediately yields the Peltier coefficient.

li = I-In(pf/pn),

(54)

where

1-I n

is the normal-state Peltier coefficient, Pn is the normal-state resistivity,

and Pr is the flux flow resistivity. Thus, one expects a similar kind of broadening

transition for T < T c as observed for the Seebeck effect and the flux flow

resistivity.

524

Chapter

10:

Thermal Properties

Fig.

10.23.

15-

10-

l'a I B=0.05 T

A ~ ! T=91.6 K

o 1.0

Time (s

-15-

-20

-25

B=0.1 T -~ ~ B=0

l" , , , 1

70 80 90 I00 II0

Temperature (K)

120 130

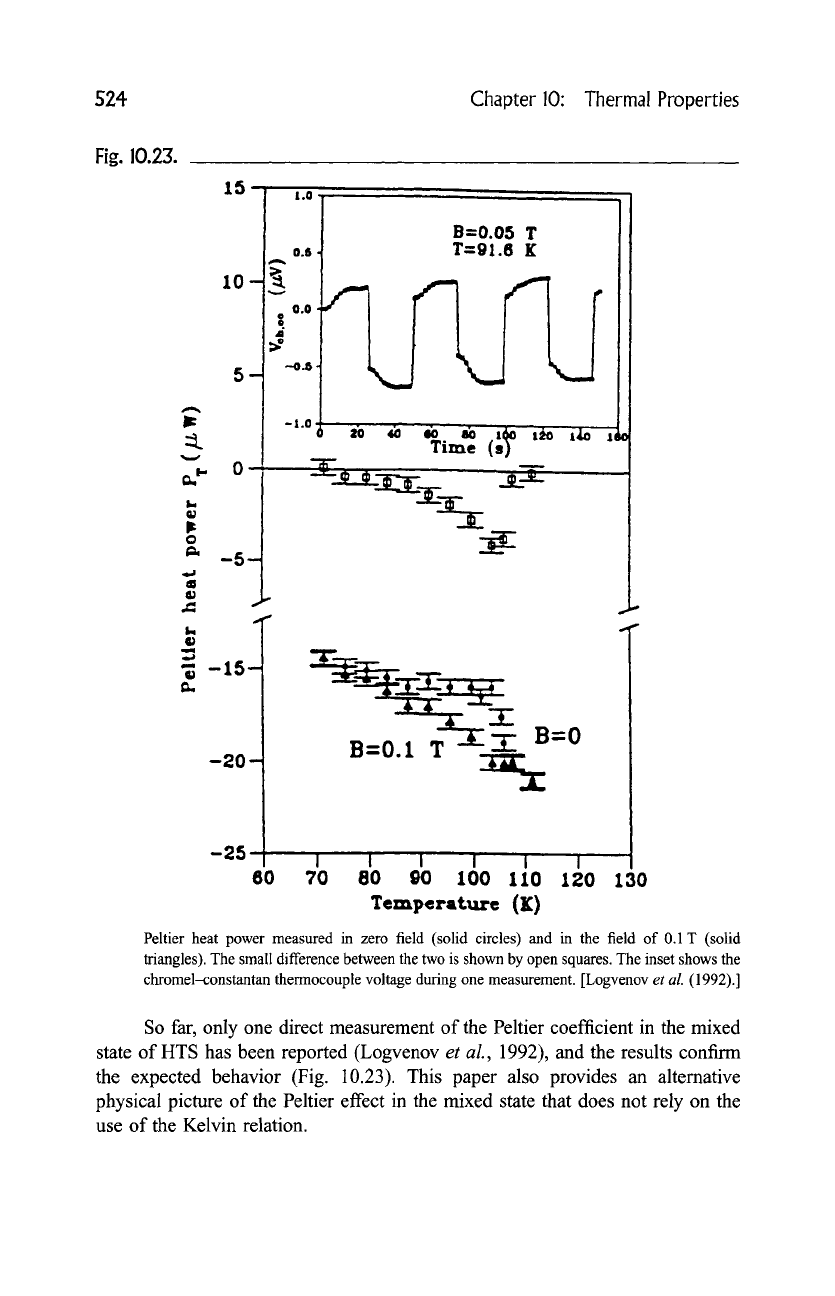
Peltier heat power measured in zero field (solid circles) and in the field of 0.1 T (solid

triangles). The small difference between the two is shown by open squares. The inset shows the

chromel-constantan thermocouple voltage during one measurement. [Logvenov

et al. (1992).]

So far, only one direct measurement of the Peltier coefficient in the mixed

state of HTS has been reported (Logvenov

et al.,

1992), and the results confirm

the expected behavior (Fig. 10.23). This paper also provides an alternative

physical picture of the Peltier effect in the mixed state that does not rely on the

use of the Kelvin relation.

D. Thermoelectric and Thermomagnetic Effects

525

e. Ettingshausen Effect

The Ettingshausen effect is the transverse equivalent of the Peltier effect

except that the coefficient itself is defined in terms of the transverse temperature

gradient rather than the transverse heat flow. With the electric current in the x-

direction and the magnetic field along the z-axis, the Ettingshausen coefficient is

defined as

e = VyV/(jxBz),

withjy =

qy = Vx T

= 0. (55)

Just as the Peltier effect is the basis of the thermoelectric refrigerator, the

Ettingshausen effect serves as the means for thermomagnetic cooling (Goldsmid,

1986).

It is easy to apply the Ettingshausen effect to the mixed state of a

superconductor. The essential point is that the core of a vortex is normal, that

is, it has higher entropy than the surrounding superconducting phase. Thus, a

vortex in motion represents the transport of entropy. Referring to Fig. 10.14

where the transport current Jx exerts the Lorentz force on the vortex given by Eq.

(36), the vortex will move in the negative y-direction. The flow of vortices is

sustained by their generation at the upper edge of the specimen and their

annihilation at the opposite edge. Since vortices carry entropy, there is absorption

of heat at the upper edge and liberation of heat at the other edge. Consequently, a

thermal gradient

VyT

is set up. Moving vortices represent heat current density

that is balanced by ordinary heat conduction once the steady state is established.

qq =_ n TS4) VL.y = - tCyAyT.

(56)

Here n is the density of vortices, S+ is the transport entropy per unit length of

vortex, and toy is the thermal conductivity in the direction of the vortex motion.

According to Eq. (38), this same vortex flow generates the longitudinal (x-axis)

electric field

E x =--VL,yBz,

which, upon substitution into Eq. (56) and writing

B z = nd?o,

yields

VyT = (rs4~Cy/C~o)E x.

(57)

Proportionality of

7yT

and Ex is a manifestation of the Ettingshausen effect.

Substituting for E~ from Eq. (39), one obtains the Ettingshausen coefficient

- %r/(i~Bz) = rs~/~.

(58)

Thermodynamics requires the transport entropy S~ to vanish at T = 0. This is no

problem since at and near absolute zero, no quasiparticle excitations exist within

the vortex core because of a gap in the excitation spectrum. The transport entropy

also vanishes at T c because vortices have filled the entire sample volume and the

sample has become normal. Thus, one expects a maximum for the transport

entropy (and for the measured transverse thermal gradient

VyT)

somewhere

between the absolute zero and T c.