Poole Ch.P., Jr. Handbook of Superconductivity
Подождите немного. Документ загружается.


576 Chapter 13: Mechanical Properties
Uemura and Takayanagi (1966) developed expressions for the shear
modulus and Poisson's ratio in an elastic two-phase system; Reddy
et al.
(1995), taking the inclusions to be voids, applied those expressions and found
G (7 - 5Vo) (1 - p)
= (24)
G O 15(1 -
Vo) p +
(7 - 5Vo)(1 - p)
B 4G0(1 -p)
9 (25)
Bo 4Go + 3Bop
Ledbetter
et al.
(Ledbetter and Datta, 1986; Ledbetter
et al.,
1994) applied
scattering theory to a homogeneous composite material consisting of a random
distribution of spheroidal particles in a continuum matrix. By considering the
inclusions to be massless voids with zero elastic resistance to shear and dilatation,
the shear and bulk moduli were expressed as
1
Go - 2--~1 [-A2
+ (A 2 - 4A1A3) '/2]
(26)
4G~
(27)
B~ -- 4(1 -
p)G o - 3pB
A 1 -8(1 -p),
A 2 - (3 -
2p)B - (8 + 4p)G,A 3 _
-3(1
+p)BG.
(28)
d. Property Data
Data for elastic properties are given in Tables 13.2 to 13.5. The elastic modulus
did not exceed 200 GPa for any material in Table 13.2, and the typical value was
on the order of only 100 GPa. The Bi : 2212 and Bi(Pb) : 2223 materials tended to
have an elastic modulus of less than 50 GPa, with the exception of one study
(Chang
et al.,
1993) that found highly anisotropic results for highly textured
Bi:2212 (nearly 120GPa in the ab-plane and about 45GPa along the c-axis).
Values of Poisson's ratio, Tablel3.5, were in the range from 0.1 to 0.3.
C
Strength
High-T c superconductors are predominantly brittle materials; that is, in a plot of
tensile stress vs strain, as illustrated schematically in Fig. 13.1, there is a critical
strain at which the material fractures. This situation is distinct from the behavior
of metals that deform plastically prior to the occurrence of material failure.
Conceptually, brittle fracture is the catastrophic propagation of a crack through
continguous regions of a material body resulting in the rupture of that body into
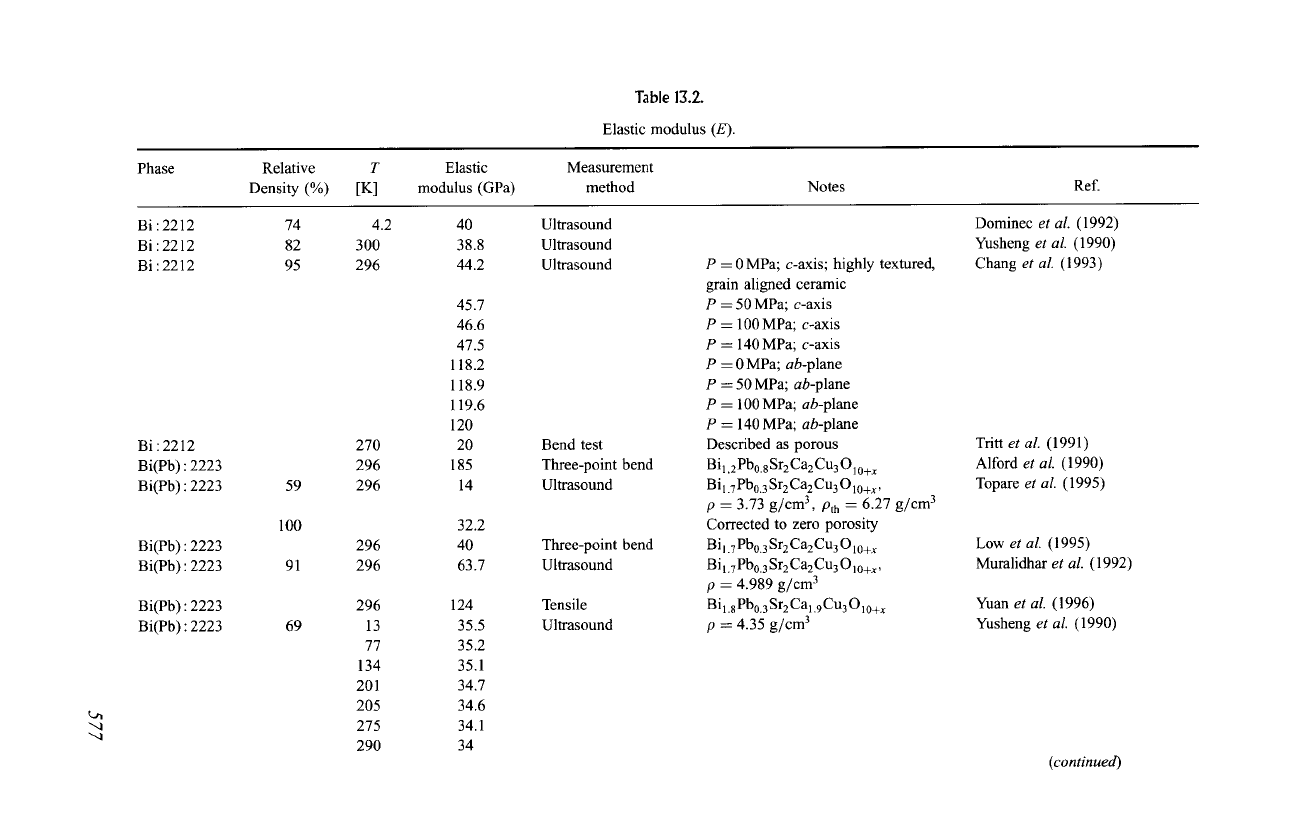
Table 13.2.
Elastic modulus (E).
Phase
Relative
T
Density (%) [K]
Elastic
modulus (GPa)
Measurement
method
Notes
Ref.
-.q
"--.I
Bi" 2212 74 4.2 40
Bi" 2212 82 300 38.8
Bi" 2212 95 296 44.2
Bi'2212
Bi(Pb)" 2223
Bi(Pb) 9 2223
Bi(Pb) 9 2223
Bi(Pb)" 2223
Bi(Pb)" 2223
Bi(Pb) 9 2223
59
100
91
69
270
296
296
296
296
296
13
77
134
201
205
275
290
45.7
46.6
47.5
118.2
118.9
119.6
120
20
185
14
32.2
40
63.7
124
35.5
35.2
35.1
34.7
34.6
34.1
34
Ultrasound
Ultrasound
Ultrasound
Bend test
Three-point bend
Ultrasound
Three-point bend
Ultrasound
Tensile
Ultrasound
P = 0 MPa; c-axis; highly textured,
grain aligned ceramic
P = 50 MPa; c-axis
P = 100 MPa; c-axis
P -- 140 MPa; c-axis
P -- 0 MPa; ab-plane
P -- 50 MPa; ab-plane
P = 100 MPa; ab-plane
P -- 140 MPa; ab-plane
Described as porous
Bi 1,2 Pbo.8 Sr2 Ca2 Cu30 lO+x
B i 1.7 Pbo.3 Sr2 Ca2 Cu30 lO+x,
p = 3.73 g/cm 3, Pth = 6.27 g/cm 3
Corrected to zero porosity
Bil.vPbo.3 Sr2CazCu30lo+x
B i 1.7 Pbo.3 S r 2 Ca 2 Cu3010+x,
p = 4.989 g/cm 3
B i 1.8 Pb0.3 Sr2 Ca 1.9 Cu30 lO+x
p = 4.35 g/cm 3
Dominec
et al.
(1992)
Yusheng
et al.
(1990)
Chang
et al.
(1993)
Tritt
et al.
(1991)
Alford
et al.
(1990)
Topare
et al.
(1995)
Low
et aL
(1995)
Muralidhar
et al.
(1992)
Yuan
et al.
(1996)
Yusheng
et al.
(1990)
(continued)
t.n
",,4
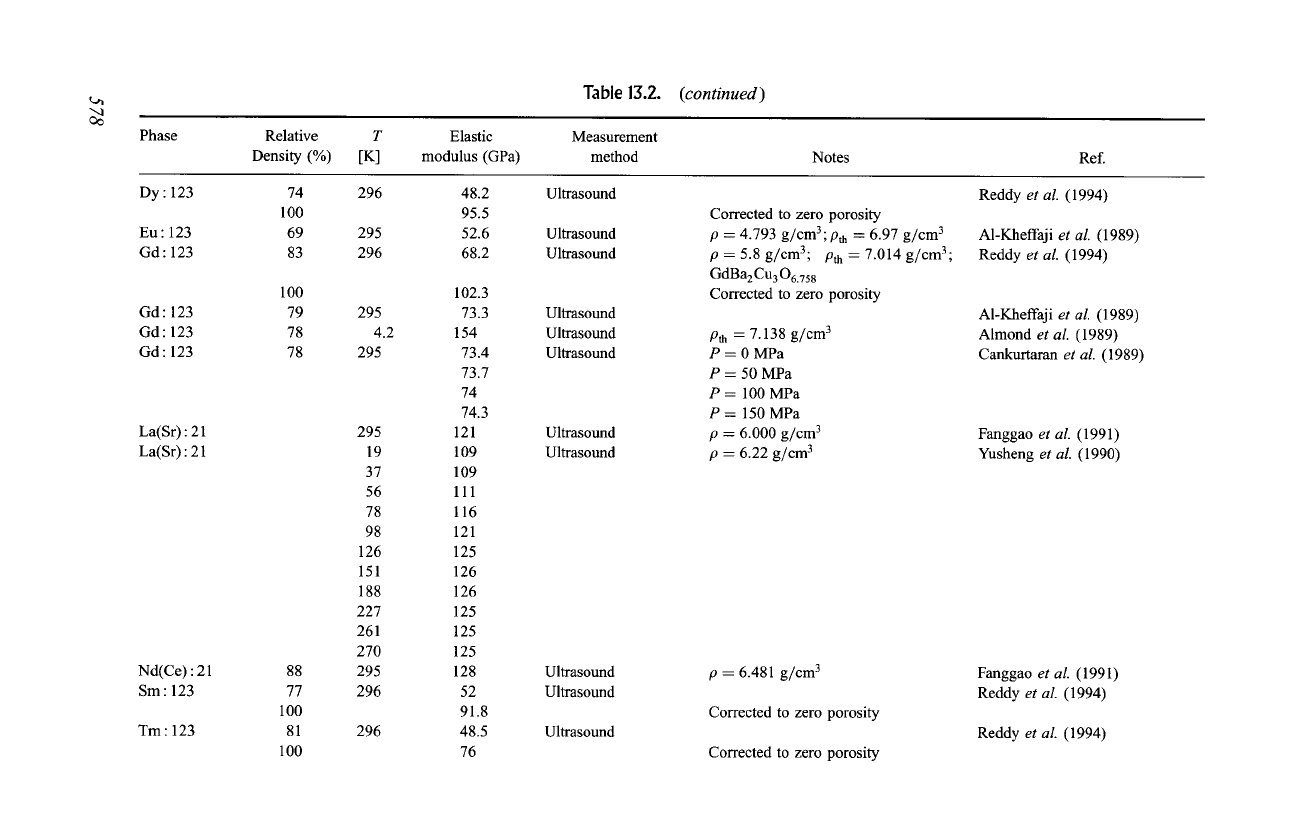
Table 13.2.
(continued)
Phase
Relative
T
Density (%) [K]
Elastic
modulus (GPa)
Measurement
method
Notes
Ref.
Dy" 123 74 296 48.2
100 95.5
Eu" 123 69 295 52.6
Gd" 123 83 296 68.2
Gd" 123
Gd" 123
Gd" 123
La(Sr) 9 21
La(Sr) 9 21
Nd(Ce) 9 21
Sm" 123
Tm" 123
100
79
78
78
88
77
100
81
100
295
4.2
295
295
19
37
56
78
98
126
151
188
227
261
270
295
296
296
102.3
73.3
154
73.4
73.7
74
74.3
121
109
109
111
116
121
125
126
126
125
125
125
128
52
91.8
48.5
76
Ultrasound
Ultrasound
Ultrasound
Ultrasound
Ultrasound
Ultrasound
Ultrasound
Ultrasound
Ultrasound
Ultrasound
Ultrasound
Corrected to zero porosity
p = 4.793 g/cm3; Pth = 6.97 g/cm 3
p = 5.8 g/cm 3" Pth = 7.014 g/cm3;
GdBa2Cu3 O6.758
Corrected to zero porosity
Pth = 7.138 g/cm 3
P =0 MPa
P = 50 MPa
P = 100 MPa
P = 150 MPa
p = 6.000 g/cm 3
p = 6.22 g/cm 3
p = 6.481 g/cm 3
Corrected to zero porosity
Corrected to zero porosity
Reddy
et aL
(1994)
A1-Kheffaji
et al.
(1989)
Reddy
et al.
(1994)
A1-Kheffaji
et al.
(1989)
Almond
et al.
(1989)
Cankurtaran
et aL
(1989)
Fanggao
et aL
(1991)
Yusheng
et al.
(1990)
Fanggao
et aL
(1991)
Reddy
et aL
(1994)
Reddy
et al.
(1994)
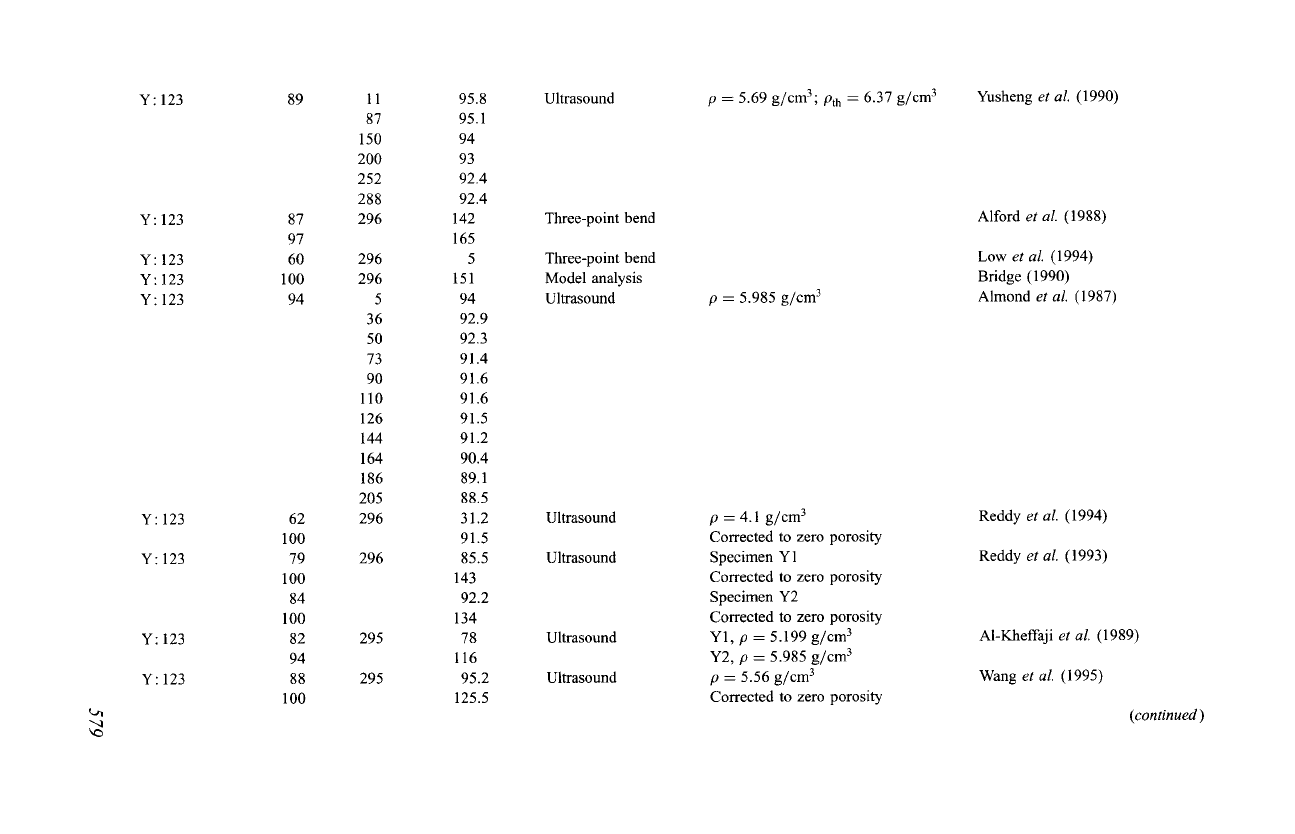
..q
Y: 123
Y: 123
Y: 123
Y: 123
Y: 123
Y: 123
Y: 123
Y: 123
Y: 123
89
87
97
60
100
94
62
100
79
100
84
100
82
94
88
100
11
87
150
200
252
288
296
296
296
5
36
5O
73
90
110
126
144
164
186
205
296
296
295
295
95.8
95.1
94
93
92.4
92.4
142
165
5
151
94
92.9
92.3
91.4
91.6
91.6
91.5
91.2
90.4
89.1
88.5
31.2
91.5
85.5
143
92.2
134
78
116
95.2
125.5
Ultrasound
Three-point bend
Three-point bend
Model analysis
Ultrasound
Ultrasound
Ultrasound
Ultrasound
Ultrasound
p = 5.69 g/cm3; Pth = 6.37 g/cm 3
p = 5.985 g/cm 3
p = 4.1 g/cm 3
Corrected to zero porosity
Specimen Y1
Corrected to zero porosity
Specimen Y2
Corrected to zero porosity
Y1, p -- 5.199 g/cm 3
Y2, p = 5.985 g/cm 3
p = 5.56 g/cm 3
Corrected to zero porosity
Yusheng
et al.
(1990)
Alford
et al.
(1988)
Low
et al.
(1994)
Bridge (1990)
Almond
et al.
(1987)
Reddy
et al.
(1994)
Reddy
et al.
(1993)
A1-Kheffaji
et al.
(1989)
Wang
et al.
(1995)
(continued)
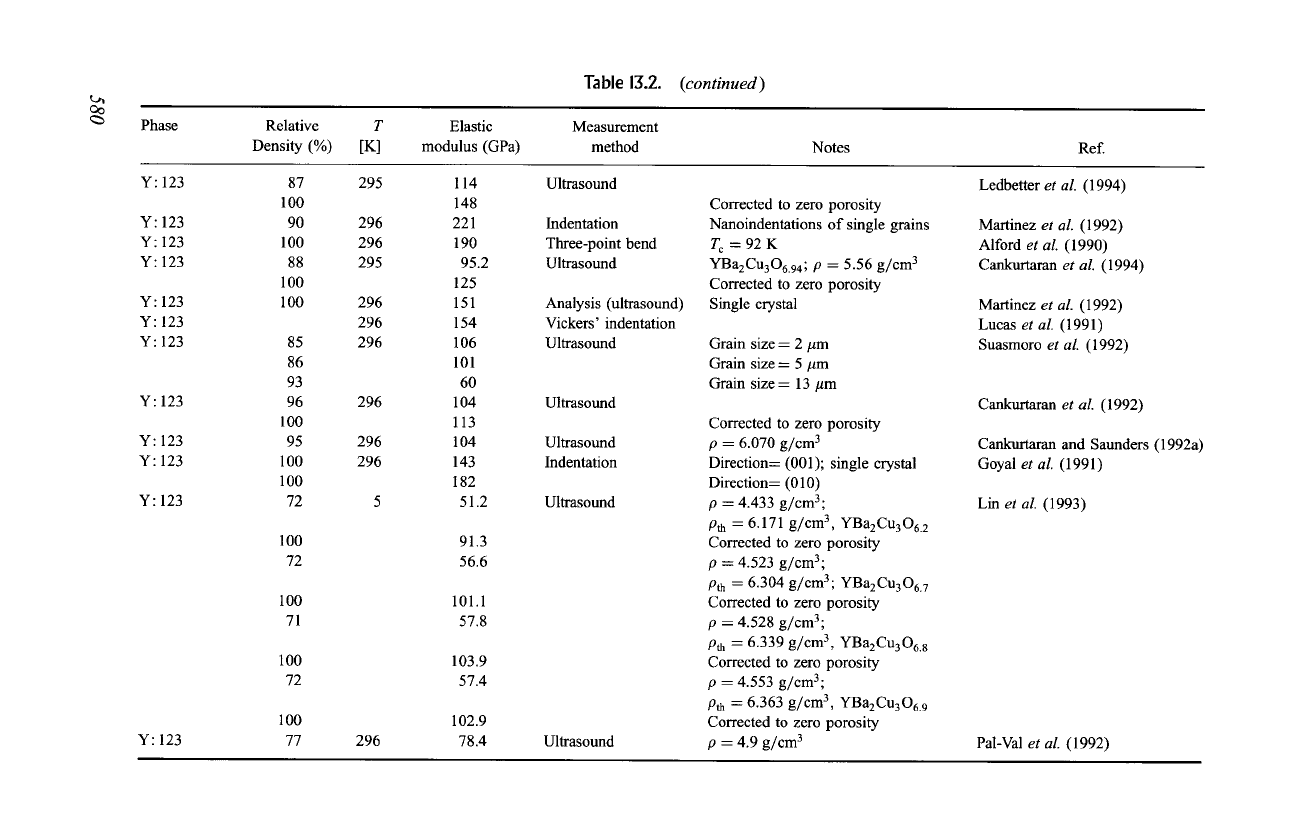
oo
Table 13.2.
(continued)
Phase
Relative
Density (%)
T
[K]
Elastic
modulus (GPa)
Measurement
method
Notes
Ref.
Y: 123
Y: 123
Y: 123
Y: 123
Y: 123
Y: 123
Y: 123
Y: 123
Y: 123
Y: 123
Y: 123
Y" 123
87
100
90
100
88
100
100
85
86
93
96
100
95
100
100
72
100
72
100
71
100
72
100
77
295
296
296
295
296
296
296
296
296
296
5
296
114
148
221
190
95.2
125
151
154
106
101
60
104
113
104
143
182
51.2
91.3
56.6
101.1
57.8
103.9
57.4
102.9
78.4
Ultrasound
Indentation
Three-point bend
Ultrasound
Analysis (ultrasound)
Vickers' indentation
Ultrasound
Ultrasound
Ultrasound
Indentation
Ultrasound
Ultrasound
Corrected to zero porosity
Nanoindentations of single grains
Tc =92K
YBa2Cu306.94; p = 5.56 g/cm 3
Corrected to zero porosity
Single crystal
Grain size = 2 #m
Grain size = 5 #m
Grain size - 13 #m
Corrected to zero porosity
p = 6.070 g/cm 3
Direction= (001); single crystal
Direction= (010)
p = 4.433 g/cm3;
Pth = 6.171 g/cm 3, YBa2Cu306. 2
Corrected to zero porosity
p = 4.523 g/cm3;
Pth = 6.304 g/cm3;
YBa2Cu306. 7
Corrected to zero porosity
p = 4.528 g/cm3;
Pth - 6.339 g/cm 3, YBa2Cu306. 8
Corrected to zero porosity
p = 4.553 g/cm3;
Pth = 6.363 g/cm 3,
YBa2Cu306. 9
Corrected to zero porosity
p = 4.9 g/cm 3
Ledbetter
et al.
(1994)
Martinez
et al.
(1992)
Alford
et al.
(1990)
Cankurtaran
et aL
(1994)
Martinez
et al.
(1992)
Lucas
et al.
(1991)
Suasmoro
et al.
(1992)
Cankurtaran
et al.
(1992)
Cankurtaran and Saunders (1992a)
Goyal
et al.
(1991)
Lin et al.
(1993)
Pal-Val
et al.
(1992)
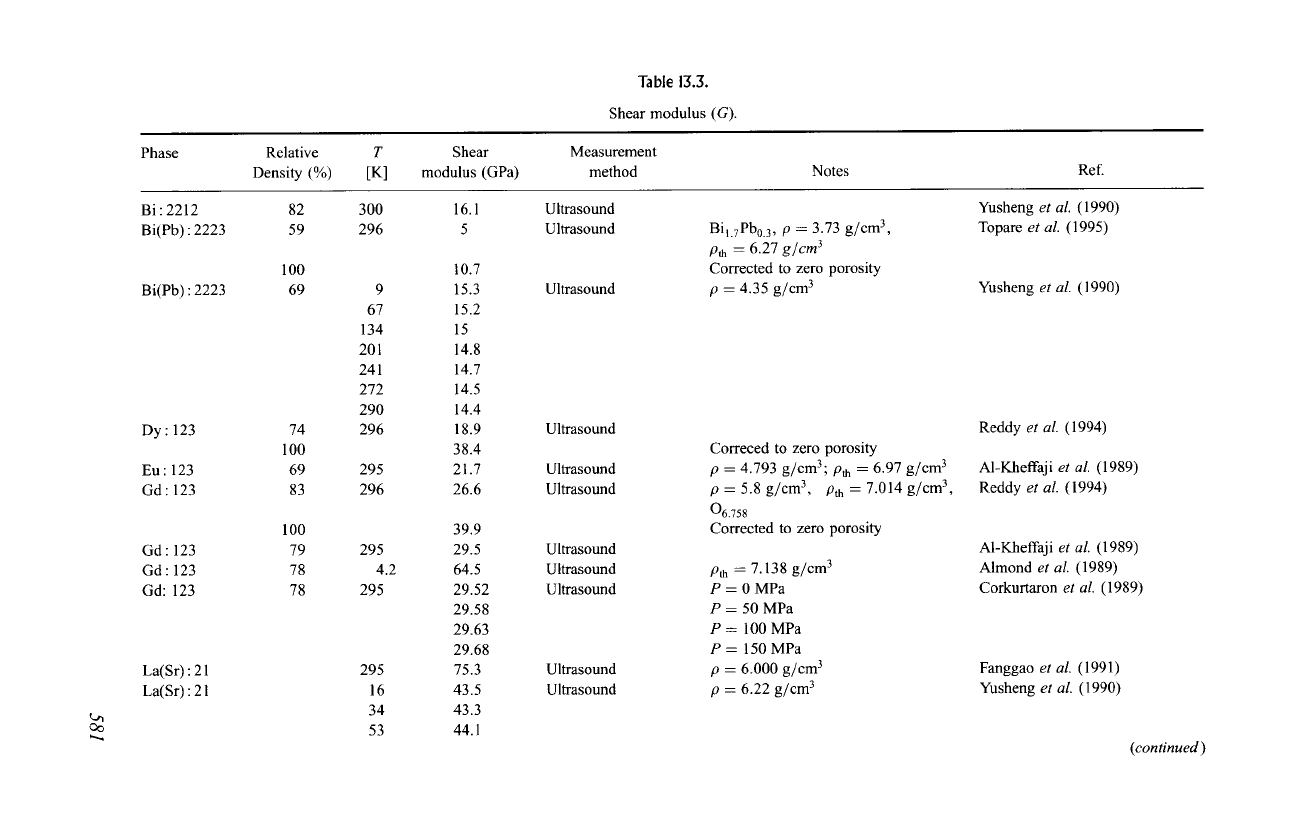
Table 13.3.
Shear modulus (G).
Phase
Relative
Density (%)
T
[K]
Shear
modulus (GPa)
Measurement
method
Notes
Ref.
Bi:2212
Bi(Pb) : 2223
Bi(Pb) :2223
Dy: 123
Eu: 123
Gd : 123
Gd : 123
Gd : 123
Gd: 123
La(Sr) : 21
La(Sr) : 21
82
59
100
69
74
100
69
83
100
79
78
78
300
296
9
67
134
201
241
272
290
296
295
296
295
4.2
295
295
16
34
53
16.1
5
10.7
15.3
15.2
15
14.8
14.7
14.5
14.4
18.9
38.4
21.7
26.6
39.9
29.5
64.5
29.52
29.58
29.63
29.68
75.3
43.5
43.3
44.1
Ultrasound
Ultrasound
Ultrasound
Ultrasound
Ultrasound
Ultrasound
Ultrasound
Ultrasound
Ultrasound
Ultrasound
Ultrasound
Bil.7Pb0.3, p = 3.73 g/cm 3,
Pth -- 6.27
g/cm 3
Corrected to zero porosity
p = 4.35 g/cm 3
Correced to zero porosity
p = 4.793 g/cm 3" Pth = 6.97 g/cm 3
p -- 5.8 g/cm 3, Pth = 7.014 g/cm 3,
06.758
Corrected to zero porosity
Pth -- 7.138 -'g/cm 3
P = 0 MPa
P = 50 MPa
P = 100 MPa
P = 150 MPa
p = 6.000 g/cm 3
p = 6.22 g/cm 3
Yusheng
et al.
(1990)
Topare
et al.
(1995)
Yusheng
et al.
(1990)
Reddy
et al.
(1994)
A1-Kheffaji
et al.
(1989)
Reddy
et al.
(1994)
A1-Kheffaji
et al.
(1989)
Almond
et al.
(1989)
Corkurtaron
et al.
(1989)
Fanggao
et al.
(1991)
Yusheng
et al.
(1990)
(continued)
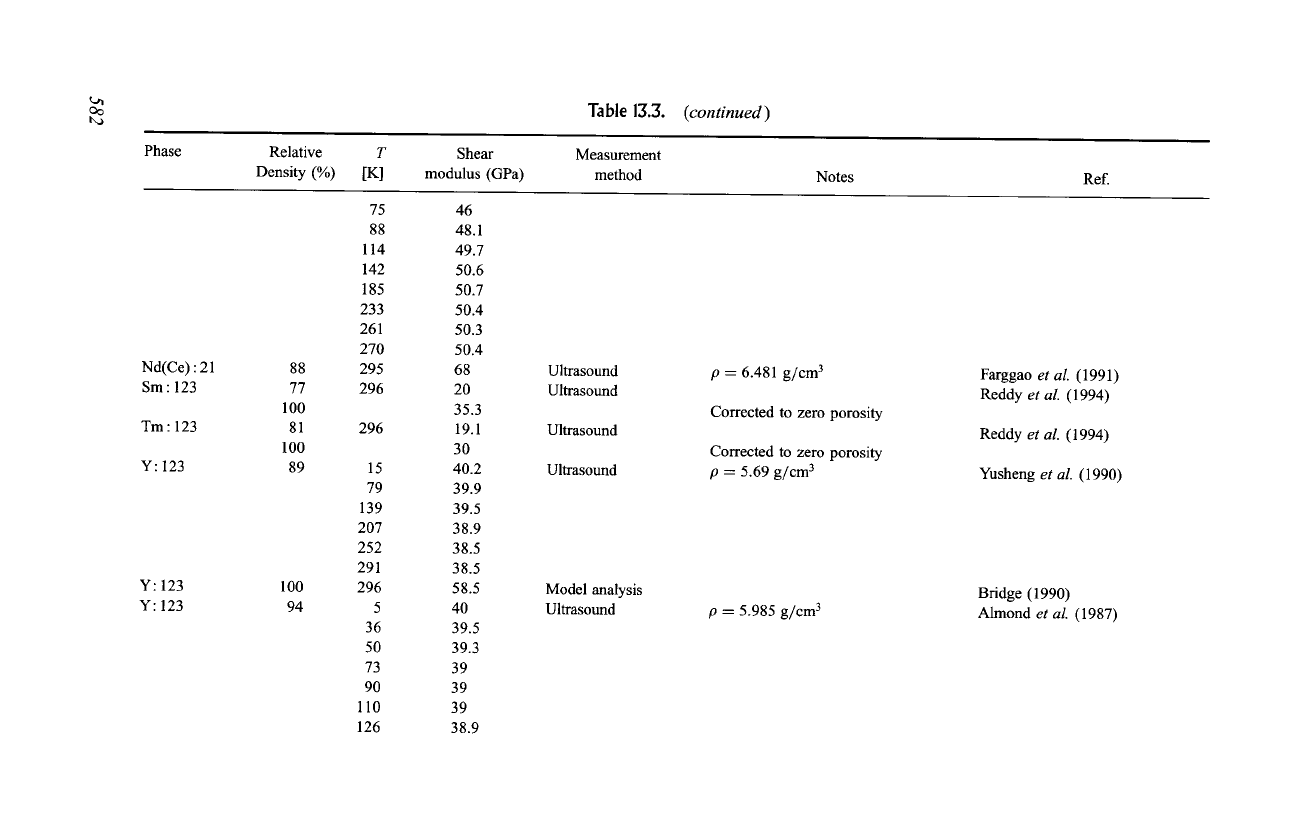
Table 13.3.
(continued)
t,,a
Phase
Relative
Density (%)
T
[K]
Shear
modulus (GPa)
Measurement
method
Notes
Ref.
Nd(Ce) 9 21
Sm" 123
Tm" 123
Y: 123
Y: 123
Y: 123
88
77
100
81
100
89
100
94
75
88
114
142
185
233
261
270
295
296
296
15
79
139
207
252
291
296
5
36
50
73
90
110
126
46
48.1
49.7
50.6
50.7
50.4
50.3
50.4
68
20
35.3
19.1
30
40.2
39.9
39.5
38.9
38.5
38.5
58.5
40
39.5
39.3
39
39
39
38.9
Ultrasound
Ultrasound
Ultrasound
Ultrasound
Model analysis
Ultrasound
p = 6.481 g/cm 3
Corrected to zero porosity
Corrected to zero porosity
p -- 5.69 g/cm 3
p = 5.985 g/cm 3
Farggao
et al.
(1991)
Reddy
et al.
(1994)
Reddy
et al.
(1994)
Yusheng
et al.
(1990)
Bridge (1990)
Almond
et al.
(1987)
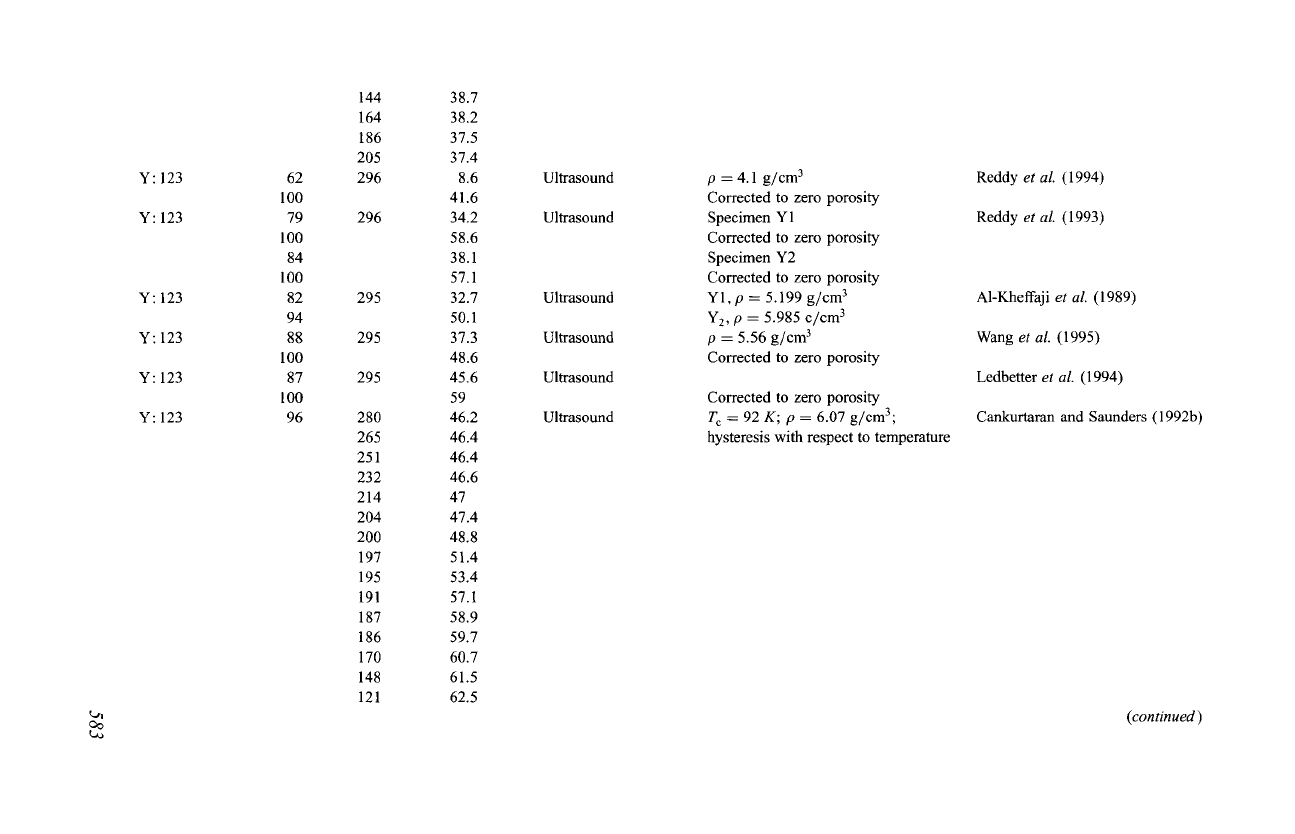
Y: 123
Y: 123
Y: 123
Y: 123
Y: 123
Y: 123
62
100
79
100
84
100
82
94
88
100
87
100
96
144
164
186
205
296
296
295
295
295
280
265
251
232
214
204
20O
197
195
191
187
186
170
148
121
38.7
38.2
37.5
37.4
8.6
41.6
34.2
58.6
38.1
57.1
32.7
50.1
37.3
48.6
45.6
59
46.2
46.4
46.4
46.6
47
47.4
48.8
51.4
53.4
57.1
58.9
59.7
60.7
61.5
62.5
Ultrasound
Ultrasound
Ultrasound
Ultrasound
Ultrasound
Ultrasound
p = 4.1 g/cm 3
Corrected to zero porosity
Specimen Y1
Corrected to zero porosity
Specimen Y2
Corrected to zero porosity
Y1, p -- 5.199 g/cm 3
Y2, P = 5.985 c/cm 3
p = 5.56 g/cm 3
Corrected to zero porosity
Corrected to zero porosity
T c = 92 K; p = 6.07 g/cm 3"
hysteresis with respect to temperature
Reddy
et al.
(1994)
Reddy
et al.
(1993)
A1-Kheffaji
et al.
(1989)
Wang
et al.
(1995)
Ledbetter
et al.
(1994)
Cankurtaran and Saunders (1992b)
(continued)
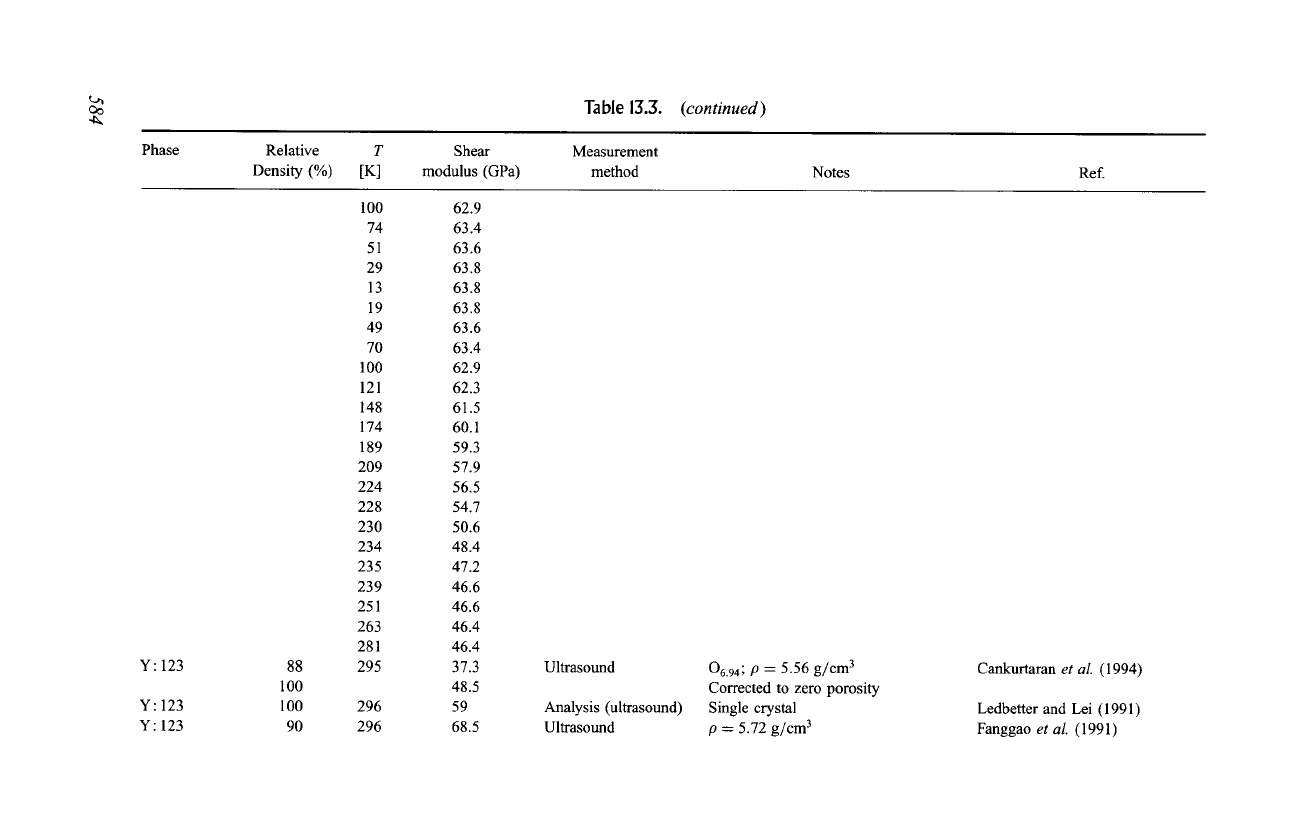
oo
4~
Table 13.3.
(continued)
Phase
Relative
T
Density (%) [K]
Shear
modulus (GPa)
Measurement
method
Notes
Ref.
Y: 123
Y: 123
Y: 123
88
100
100
90
100
74
51
29
13
19
49
70
100
121
148
174
189
209
224
228
230
234
235
239
251
263
281
295
296
296
62.9
63.4
63.6
63.8
63.8
63.8
63.6
63.4
62.9
62.3
61.5
60.1
59.3
57.9
56.5
54.7
50.6
48.4
47.2
46.6
46.6
46.4
46.4
37.3
48.5
59
68.5
Ultrasound
Analysis (ultrasound)
Ultrasound
06.94; p -- 5.56 g/cm 3
Corrected to zero porosity
Single crystal
p = 5.72 g/cm 3
Cankurtaran
et al.
(1994)
Ledbetter and Lei (1991)
Fanggao
et al.
(1991)

Y" 123
Y" 123
Y: 123
96
100
72
100
72
100
71
100
72
100
77
296
5
296
45
49
21.5
38.4
23.6
42.2
24.2
43.5
24.2
43.6
28.5
Ultrasound
Ultrasound
Ultrasound
Corrected to zero porosity
p = 4.433 g/cm3;
Pth = 6.171 g/cm 3, YBa2Cu306. 2
Corrected to zero porosity
p -- 4.523 g/cm3;
Pth -- 6.304 g/cm 3, YBa2Cu306. 7
Corrected to zero porosity
p -- 4.528 g/cm3;
Pth -- 6.339 g/cm 3, YBa2Cu306.8
Corrected to zero porosity
p -- 4.553 g/cm3;
Pth --6.363 g/cm 3, YBa2Cu306. 9
Corrected to zero porosity
p -- 4.9 g/cm 3, grain size= 10 #m
Cankurtaran
et al.
(1992)
Lin
et al.
(1993)
Pal-Val
et al.
(1992)
