Poole Ch.P., Jr. Handbook of Superconductivity

596

Chapter

13:

Mechanical Properties

two or more pieces. In this context, the term "strength" is used to indicate the

level of stress that can be sustained without catastrophic cracking. In practice, the

"strength" of a ceramic material is determined as the value of the stress, af,

attained at fracture.

a. Terms and Basic Relations

The value of the stress that is required to produce fracture depends, in part, on the

type of stress system that is applied to the material. Thus, the terminology for

fracture strength is refined somewhat according to the particular design of the

apparatus that is used to measure the fracture stress. When fracture is produced in

a specimen subjected to purely tensile stress, the result is called the tensile

strength. The fracture stress deduced from a specimen subjected to bending is

called the flexural strength (also called the bending strength and the modulus of

rupture).

For a given production lot of a ceramic material, the fracture stress is not an

invariant quantity across all specimens drawn from that lot. Rather, the strength of

a brittle material is controlled by the distribution of defects, inclusions, and

microscopic inhomogeneities that are known collectively as flaws. The measured

strength of two specific test specimens can be significantly different because the

specific flaws in two specimens are different. Thus, brittle fracture strength is best

understood in a statistical context (Davies, 1973; Batdorf, 1978; Hild and

Marquis, 1992).

The basic understanding of brittle fracture was established by Griffith

(1921). By assuming that crack extension (i.e., fracture for an ideally brittle

material) occurs when the elastic energy (which is released during crack

extension) is just sufficient to form the new surfaces, Griffith found that a flaw

will be the origin of fracture when

a c - , (29)

L rcc0 1

where E'= E for plane stress and E'=

E/(1-

y2)

for plane strain; E is the

elastic modulus; v is Poisson's ratio; 7 is the fracture energy per unit area; and 2c 0

is the initial crack size.

Since the production lot of any ceramic material, in general, possesses a

distribution of flaw sizes over the specimens drawn from the lot, there must be a

corresponding distribution of fracture strengths. Weibull (1939; 1951) showed

that the statistics of fracture could be described quite effectively by assuming a

weakest link model for the flaws. In this model, each volume element has a local

C. Strength 597

value of fracture strength, and the probability of failure,

Pf,

of the whole

specimen is given by integrating over the stressed volume:

Pf -1-expI-Iv(a/Oo)mdV/Vo],

(30)

where a 0 and m are parameters known respectively as the Weibull characteristic

strength and the Weibull modulus, and V 0 is a volume scale parameter. For

uniform stress, this expression simplifies to

Pf = 1 -- exp[-(Vs/Vo)(a/ao)m],

(31)

where V s is the volume of the test specimen.

Given Pf, the mean fracture strength can be calculated formally from the

defining relation

1

O" -- N E nf(o') 9 0",

(32)

where

nf(o)

is the number of specimens that fail at stress a and N- ~

nf(o).

Noting that the number of specimens that fail at stress a is the difference between

the number of specimens surviving at

a- da/2

and the number surviving at

a + da/2,

nf(o)

N

-- = [1 - Pf(a -

da/2)] -

[1 - Pf(a +

da/2)],

means that Eq. (32) can be recast in the form

6" - P'f . a da,

(33)

(34)

where

Uf- dPf/da.

Using Eq. (31) in this latter relation, one can obtain a

critically important result for the strength of ceramic materials: specifically, that

two sets of geometrically similar specimens having the same flaw system will

have different measured fracture strengths if the volumes of the specimens are

different. Explicitly,

(71 (_~11) 1/m

- , (35)

O" 2

which expresses the reasonable result that a larger volume will contain more flaws

by which fracture may be initiated.

b. Measurement Methods

In view of Eq. (35), meaningful comparisons of strength data across independent

studies require careful attention to the specifications of the specimens and the

strength test configurations. Consequently, there has been a considerable effort

worldwide to develop and standardize appropriate test methods.

Fig. 13.3.

Piston

Co)

Loadin~ R~---~rip

Specim

(a)

Load Cr

I

598 Chapter 13: Mechanical Properties

(c)

Schematic of a tensile test: (a) apparatus, (b) specimen with a pin-loaded grip, (c) specimen

with a shoulder-loaded grip.

The simplest test, conceptually, is the tensile test, Fig. 13.3, in which a

specimen is uniformly loaded in tension (Ohji, 1988). The fracture stress of the

specimen is then simply the ratio of the loading force, F, applied to the specimen

at the time of fracture, to the initial cross-sectional area of the specimen, A0; i.e.,

at = F/Ao.

The simplicity of this test is encumbered somewhat by the necessity

of gripping the specimen so that the tensile load can be applied to it (French and

Wiederhorn, 1996). Because of the difficulty in machining ceramics, it is

desirable to keep the shape of the specimen as simple as possible. Furthermore,

screw threads and other features with high stress concentration also need to be

avoided because of the possible fracture at the specimen grip. Two designs that

have met with some success are illustrated in Fig. 13.3. A further concern in the

tensile test is the alignment of the specimen along the tensile axis. Any

misalignment can introduce a bending moment in the specimen and thereby

affect the measured value of the fracture stress.

Another test method for determining the tensile strength is the diametral

compression test (Rudnick

et al.,

1963), Fig. 13.4. The specimen is a cylinder

with a circular cross-section. The load is applied along the length of the cylinder

and directed along a diameter of the cross-section. While a large compressive

stress exists along the load contact line, tensile stress develops in the direction

normal to the load axis in the central region of the specimen. A method of

distributed loading must be used to avoid high compressive and shear stresses at

the ends of the cylinder such that the maximum tensile stress dominates the

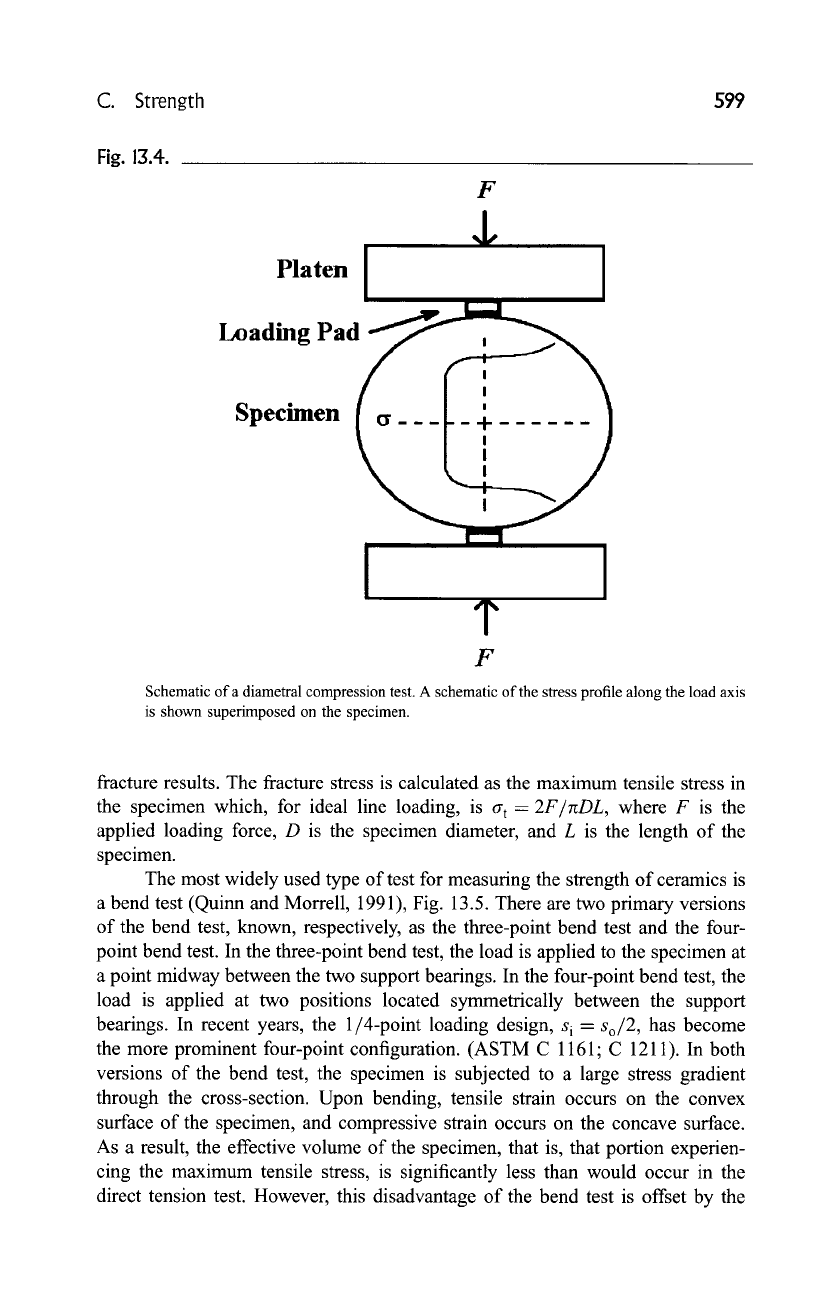
C. Strength 599

Fig. 13.4.

Platen

F

J,

Loading Pad

Specimen | ~_ __

I

!

-4

I

F

Schematic of a diametral compression test. A schematic of the stress profile along the load axis

is shown superimposed on the specimen.

fracture results. The fracture stress is calculated as the maximum tensile stress in

the specimen which, for ideal line loading, is at =

2F/nDL,

where F is the

applied loading force, D is the specimen diameter, and L is the length of the

specimen.

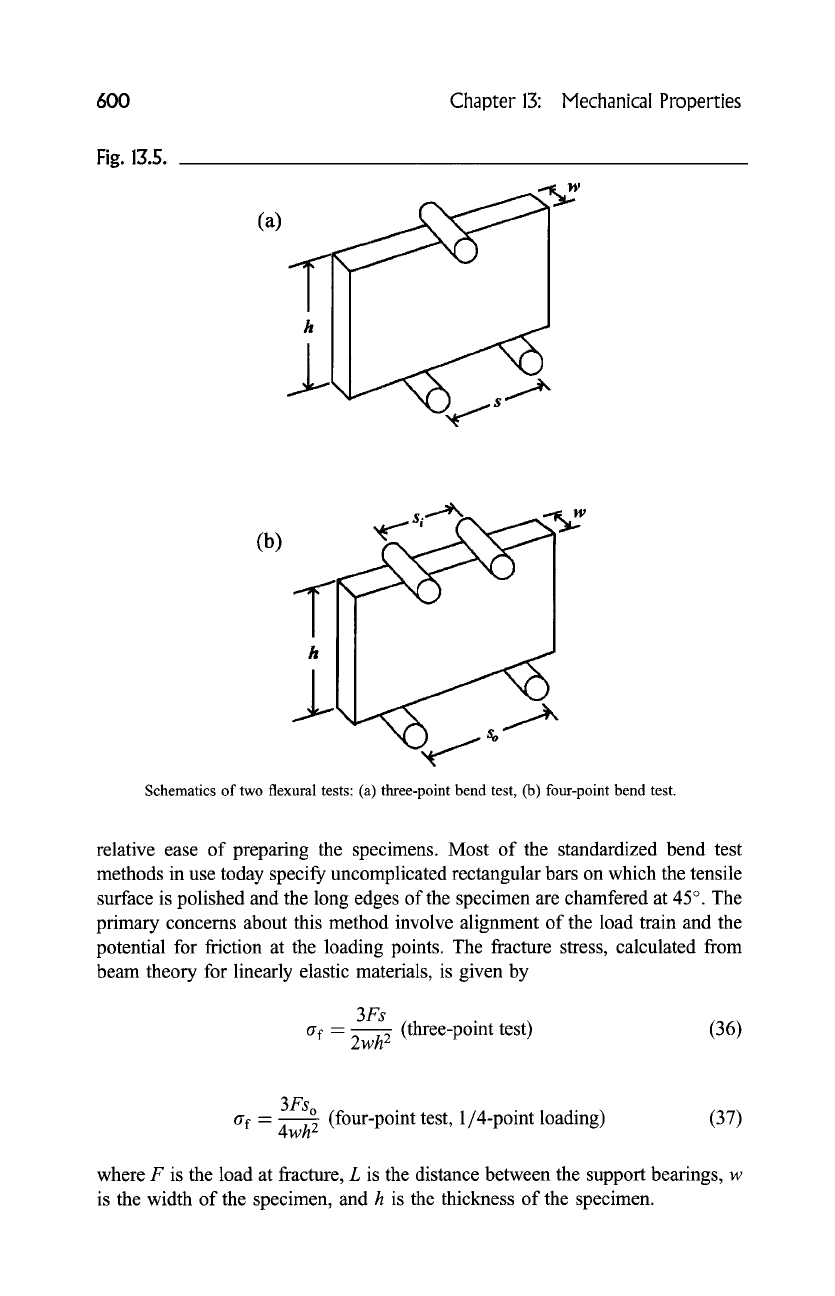
The most widely used type of test for measuring the strength of ceramics is

a bend test (Quinn and Morrell, 1991), Fig. 13.5. There are two primary versions

of the bend test, known, respectively, as the three-point bend test and the four-

point bend test. In the three-point bend test, the load is applied to the specimen at

a point midway between the two support beatings. In the four-point bend test, the

load is applied at two positions located symmetrically between the support

beatings. In recent years, the 1/4-point loading design, s i =

So~2,

has become

the more prominent four-point configuration. (ASTM C 1161; C 1211). In both

versions of the bend test, the specimen is subjected to a large stress gradient

through the cross-section. Upon bending, tensile strain occurs on the convex

surface of the specimen, and compressive strain occurs on the concave surface.

As a result, the effective volume of the specimen, that is, that portion experien-

cing the maximum tensile stress, is significantly less than would occur in the

direct tension test. However, this disadvantage of the bend test is offset by the

600

Chapter

13:

Mechanical Properties

Fig. 13.5.

(a)

(b)

h

L

) /so"

Schematics of two flexural tests: (a) three-point bend test, (b) four-point bend test.

relative ease of preparing the specimens. Most of the standardized bend test

methods in use today specify uncomplicated rectangular bars on which the tensile

surface is polished and the long edges of the specimen are chamfered at 45 ~ . The

primary concerns about this method involve alignment of the load train and the

potential for friction at the loading points. The fracture stress, calculated from

beam theory for linearly elastic materials, is given by

3Fs

tYf "--

2wh2

(three-point test) (36)

3Fs~

(four-point test,

1/4-point

loading)

ff f - 4wh2

(37)

where F is the load at fracture, L is the distance between the support beatings, w

is the width of the specimen, and h is the thickness of the specimen.

O. Hardness 601

c. Property Data

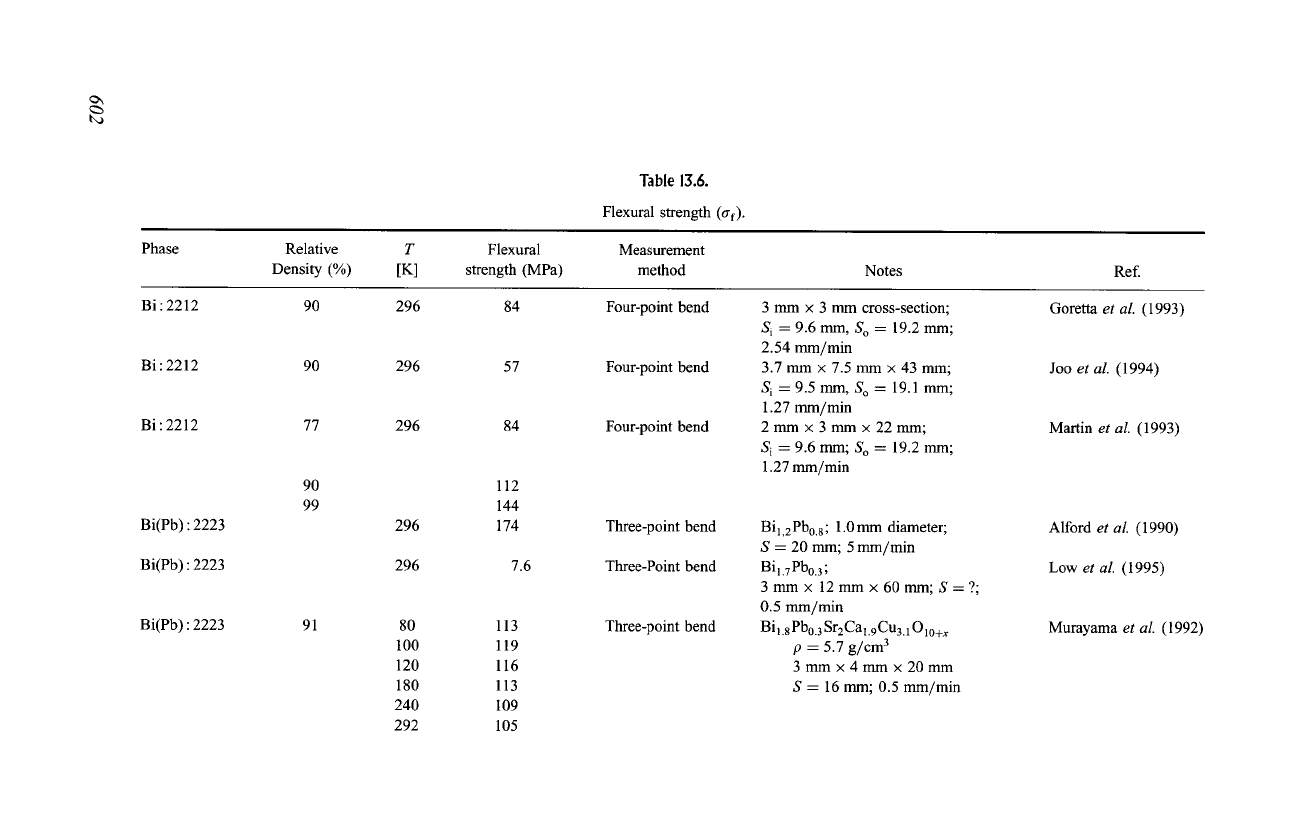
Strength data are given in Tables 13.6 and 13.7. Although there is only a small

amount of flexural strength data in Table 13.6, the results are sufficient to indicate

a strong dependence on both the density and the grain size. The largest flexural

strength in this table is a relatively low 216 MPa for Y: 123, and the largest tensile

strength in Table 13.7 is only 103 MPa for Bi(Pb) : 2223.

D

Hardness

Hardness is a property that is widely used for quality control and as a relative

performance parameter, but that is considered to have little merit as an intrinsic

material property. This situation stems from the empirical nature of its definition.

Hardness is an engineering property that is used to quantify the resistance of a

material to irreversible deformation (McColm; 1990). Because of its empirical

definition, measurement of the property requires that an irreversible deformation

be produced as an integral part of the measurement process. How the deformation

is produced determines what particular definition of hardness is being used. As a

result, there are numerous hardness values that may be quoted, and there is no

established method of converting one hardness scale to another. Nevertheless,

hardness has evolved as an important property in homogeneity studies, process

control, and material selection. The popularity of hardness testing may be due in

part to the relative ease of conducting the test, its relatively low cost, and its

basically nondestructive nature.

a. Terms and Basic Relations

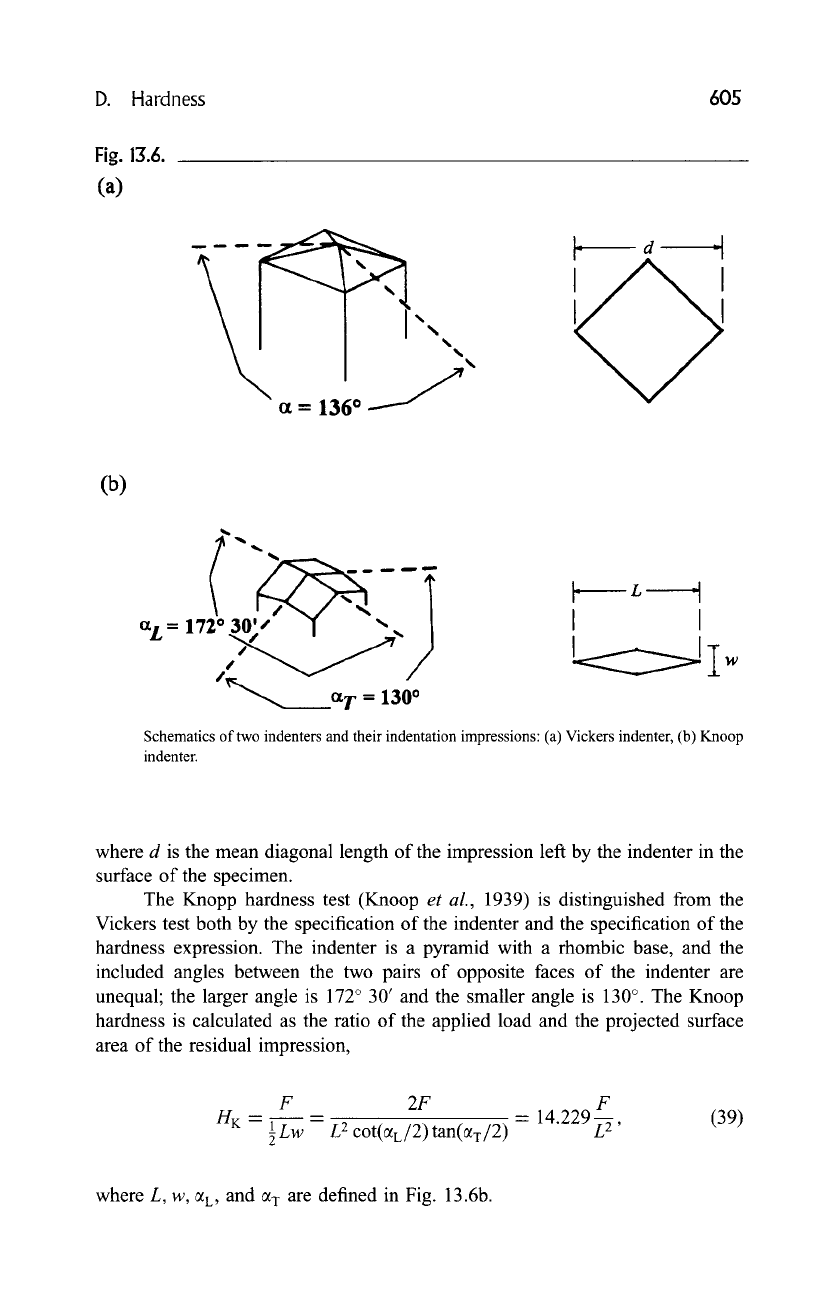
Two hardness tests, the Vickers hardness test and the Knoop hardness test, have

become widely used for advanced ceramics. These tests belong to the subclass

referred to as indentation hardness tests. In both tests, an object, called an indenter,

is pressed into a locally flat, polished surface of the specimen. The applied load

and the residual impression of the indenter, Fig. 13.6, determine the hardness.

In the Vickers hardness test (ASTM E 92; E384), the indenter is a pyramid

with a square base and with an included angle between opposite faces of

= 136 ~ The Vickers hardness is calculated as the ratio of the applied load,

F, and the actual surface area of the residual impression;

2F sin(~/2) F

H v = d2 = 1.8544 d- 5 , (38)

t,,a

Table 13.6.

Flexural strength (o-f).

Phase

Relative

Density (%)

T

[K]

Flexural

strength (MPa)

Measurement

method

Notes

Ref.

Bi'2212

Bi(Pb)" 2223

Bi(Pb) 9 2223

Bi(Pb)" 2223

90

77

90

99

91

296

80

100

120

180

240

292

84

57

84

112

144

174

7.6

113

119

116

113

109

105

Four-point bend

Three-point bend

Three-Point bend

Three-point bend

3 mm x 3 mm cross-section;

Si = 9.6 mm, S O -- 19.2 mm;

2.54 mm/min

3.7 mm x 7.5 mm x 43 mm;

Si -- 9.5 mm, S O = 19.1 mm;

1.27 mm/min

2 mm x 3 mm x 22 mm;

Si -- 9.6 mm; S O = 19.2 mm;

1.27 mm/min

Bi 1,2Pbo.8; 1.0 mm diameter;

S = 20 mm; 5 mm/min

Bil.7Pbo.3;

3mmx 12mmx60mm;S=?;

0.5 mm/min

B i 1.8 Pbo.3 Sr2 Ca 1.9 Cu3.1010+x

p = 5.7 g/cm 3

3 mm x 4mm x 20mm

S -- 16 mm; 0.5 mm/min

Goretta

et al.

(1993)

Joo

et al.

(1994)

Martin

et al.

(1993)

Alford

et al.

(1990)

Low

et al.

(1995)

Murayama

et al.

(1992)

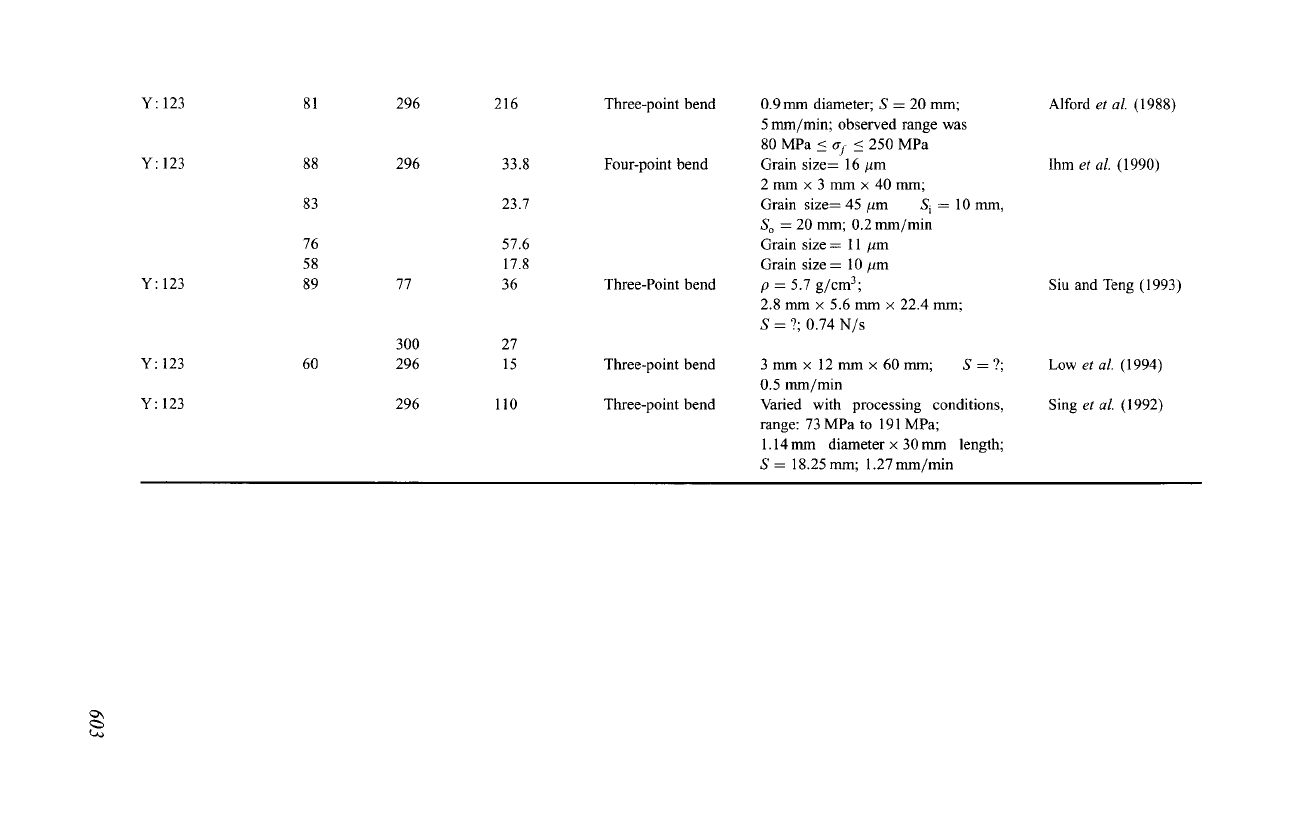
Y" 123

81

88

83

76

58

89

60

296

77

300

296

216

33.8

23.7

57.6

17.8

36

27

15

110

Three-point bend

Four-point bend

Three-Point bend

Three-point bend

0.9 mm diameter; S = 20 mm;

5 mm/min; observed range was

80 MPa _<

O'f

~ 250 MPa

Grain size= 16/~m

2 mm x 3 mm x 40mm;

Grain size= 45 #m S i = 10 mm,

S o = 20 mm; 0.2 mm/min

Grain size= 11 ~tm

Grain size = 10 #m

p = 5.7 g/cm 3"

2.8 mm x 5.6 mm x 22.4 mm;

S = ?; 0.74 N/s

3mmx 12mmx60mm; S=?;

0.5 mm/min

Varied with processing conditions,

range: 73 MPa to 191 MPa;

1.14 mm diameter x 30 mm length;

S = 18.25 mm; 1.27 mm/min

Alford

et al.

(1988)

Ihm

et al.

(1990)

Siu and Teng (1993)

Low

et al.

(1994)

Sing

et al.

(1992)

ta~

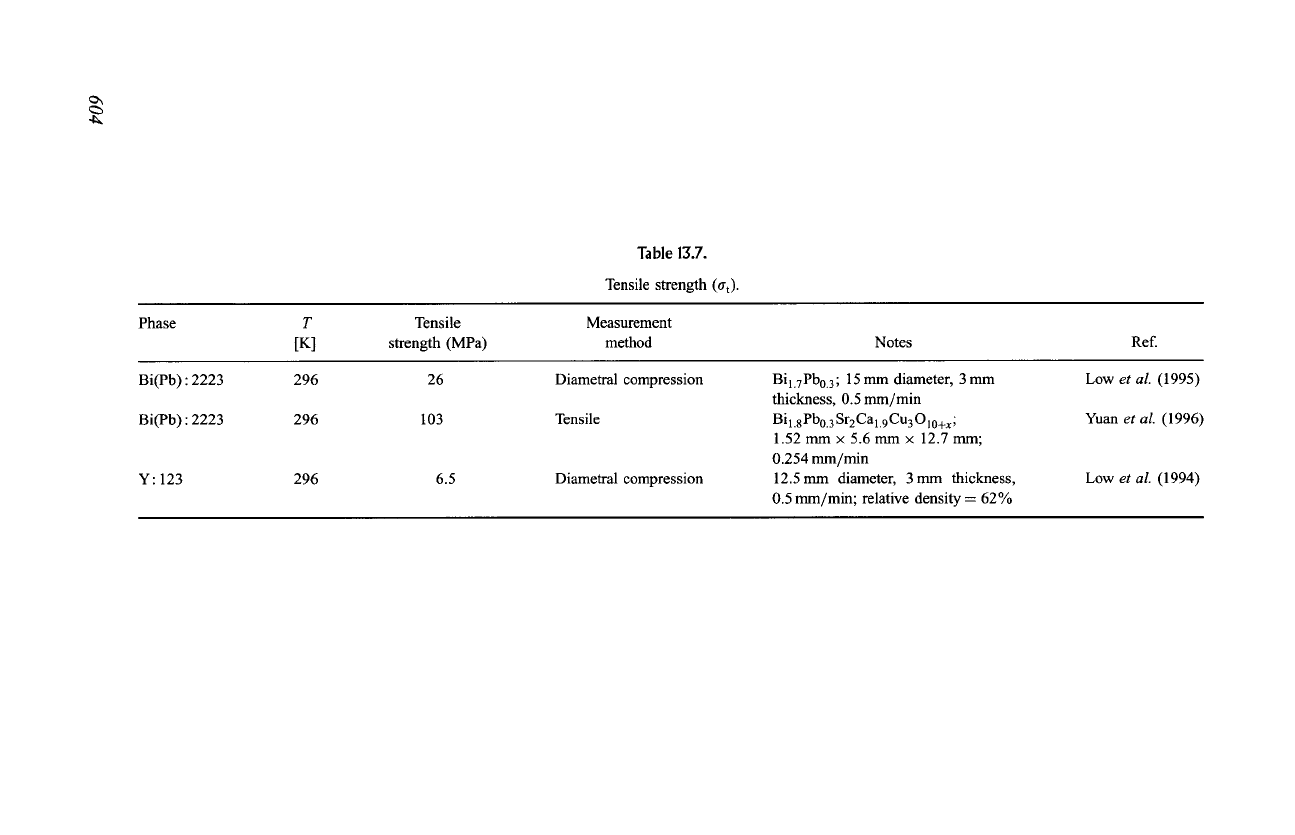
Table 13.7.

Tensile strength

(fit)"

Phase

T

[K]

Tensile

strength (MPa)

Measurement

method

Notes

Ref.

Bi(Pb):2223

Bi(Pb) : 2223

Y: 123

296

26

103

6.5

Diametral compression

Tensile

Diametral compression

Bi 1.7Pbo.3; 15 mm diameter, 3 mm

thickness, 0.5 mm/min

B i 1.8 Pbo.3 Sr2 Ca 1.9 Cu3 O 10+x;

1.52

mm • 5.6 mm

• 12.7

mm;

0.254 mm/min

12.5 mm diameter, 3 mm thickness,

0.5 mm/min; relative density--62%

Low

et al.

(1995)

Yuan

et aL

(1996)

Low

et aL

(1994)

D. Hardness 605

Fig. 13.6.

(a)

m m m ~

,.,.

a = 136 ~ J

V

I I

(b)

/,~~

cz T = 130 ~

I_ L' ' "J

I- q

I I

t<:Z:: Iw

Schematics of two indenters and their indentation impressions: (a) Vickers indenter, (b) Knoop

indenter.

where d is the mean diagonal length of the impression left by the indenter in the

surface of the specimen.

The Knopp hardness test (Knoop

et al.,

1939) is distinguished from the

Vickers test both by the specification of the indenter and the specification of the

hardness expression. The indenter is a pyramid with a rhombic base, and the

included angles between the two pairs of opposite faces of the indenter are

unequal; the larger angle is 172 ~ 30' and the smaller angle is 130 ~ The Knoop

hardness is calculated as the ratio of the applied load and the projected surface

area of the residual impression,

F 2F F

H K 1L w

L2 cot(c~L/2) tan(c~T/2) 14.229L2, (39)

where L, w, %, and a T are defined in Fig. 13.6b.

Poole Ch.P., Jr. Handbook of Superconductivity

Подождите немного. Документ загружается.