Poole Ch.P., Jr. Handbook of Superconductivity

556

Chapter

12: Magnetic

Properties

When the applied magnetic field is in the z direction, along the c axis, the

vortex has axial symmetry, its cross-section is a circle, and it has a distance

dependence

Oo

Oz(x, Y) -- 2g~2ab /2/~ab]"

(38)

When the applied field is in the x direction, along the a axis, there is no longer

axial symmetry, the cross-section is elliptical, and the distance dependence is

more complicated (Poole et al., 1995, Chap. 9).

Figure 12.7 shows vortex cross-sections for the two applied field directions.

When the applied magnetic field is aligned at an oblique angle relative to the c

direction, the expressions for the magnetic field and current density become very

complicated, with neither the internal magnetic field nor the magnetization

oriented in the same direction as Bap p.

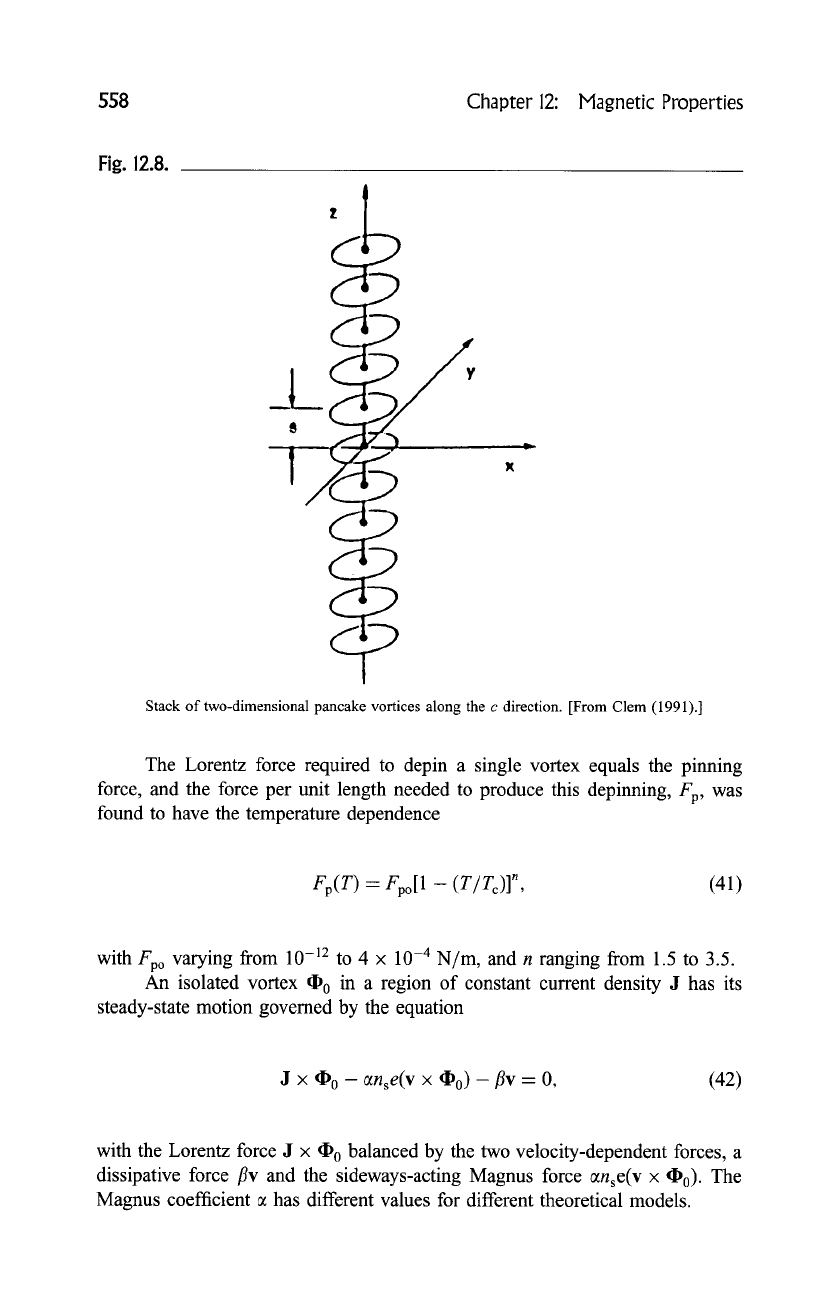
In the cuprates the coherence length ~c along the c axis is less than the

average spacing between layers of copper oxide planes, and following the

Lawrence-Doniach model (1971), the Josephson coupling between layers is

weak. A vortex perpendicular to these layers is looked upon as a stacking of two-

dimensional (2D) pancake-shaped vortices, as shown in Fig. 12.8.

Individual Vortex Motion

The repulsive force per unit length F/L between two vortices arises from the

Lorentz force interaction F -- J1 x B2 between the current density J1 from one

vortex and the magnetic field B 2 of the other:

F/L- I J1 • B2r2 dr2 d~b2.

(39)

For the hypothetical case of vortices that are far apart, d >> 2, the current density

of one vortex is fairly uniform in the neighborhood of the other, and we can make

the approximation

F/L ~ Jl(d) • I B2r2 dr2 dq~2'

(40)

where the integral is equal to the flux quantum O0, and in the high ~c

approximation Jl(d) is given by Eq. (23). For applied fields far above the

lower critical field, Bap p >> Be1, nearest-neighbor vortices overlap, i.e. are much

closer to each other than the penetration depth 2, and Eq. (40) does not apply.

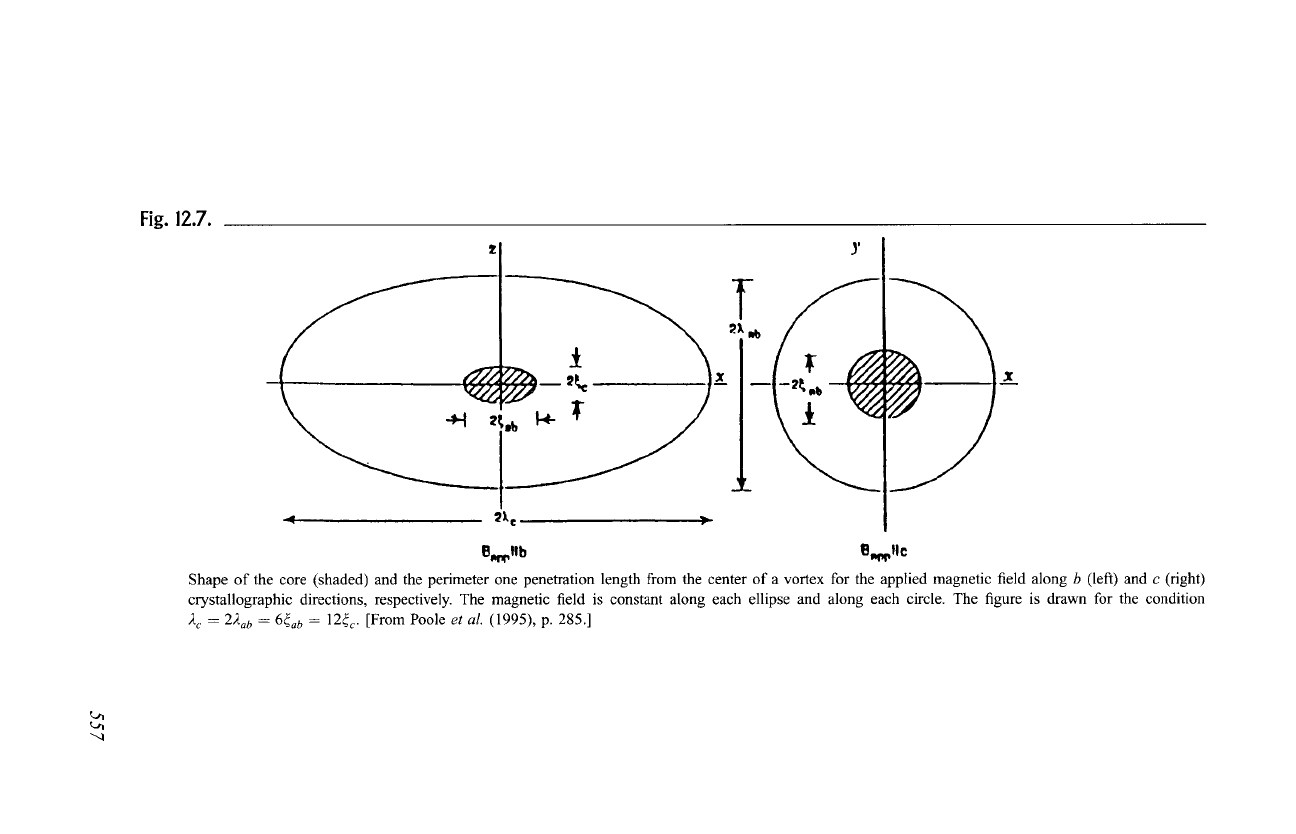
Fig. 12.7.

/

-

,

2), e

_

,,

B~II5 B~IIc

Shape of the core (shaded) and the perimeter one penetration length from the center of a vortex for the applied magnetic field along b (left) and c (right)

crystallographic directions, respectively. The magnetic field is constant along each ellipse and along each circle. The figure is drawn for the condition

2 c -- 22ab

= 6~ab = 12~ c. [From Poole

et al.

(1995), p. 285.]

"-1

558

Chapter

12:

Magnetic Properties

Fig. 12.8.

2

C)

--] ___~

Y

$

C

C.

C

1

v

Stack of two-dimensional pancake vortices along the c direction. [From Clem (1991).]

The Lorentz force required to depin a single vortex equals the pinning

force, and the force per unit length needed to produce this depinning, Fp, was

found to have the temperature dependence

Fo(T ) - Fpo[1

-

(T/Tc)] n,

(41)

with Fpo varying from 10

-12

to 4 x 10

-4

N/m, and n ranging from 1.5 to 3.5.

An isolated vortex ~0 in a region of constant current density J has its

steady-state motion governed by the equation

J x ~o - ~nse(V x ~0) -flv - 0,

(42)

with the Lorentz force J x ~0 balanced by the two velocity-dependent forces, a

dissipative force/~v and the sideways-acting Magnus force ense(V x ~o)- The

Magnus coefficient e has different values for different theoretical models.

G. Transport Current in a Magnetic Field

559

G

Transport Current in a Magnetic Field

Consider a transport current of uniform density

Jx

flowing along a superconduct-

ing wire located in a transverse magnetic field

B z.

The superconductor is

considered soft, that is, the pinning forces are not strong enough to prevent

flux motion, so three things can happen:

.

The current exerts the force J x ~0 on the vortices, causing them to move

from one side of the wire to the other. The viscous drag /~v limits this

motion to a constant velocity v~, and the Magnus force causes it to occur at

the angle | defined by the ratio of the Magnus force to the drag force,

tan | =

Cmse~o/,6.

(43)

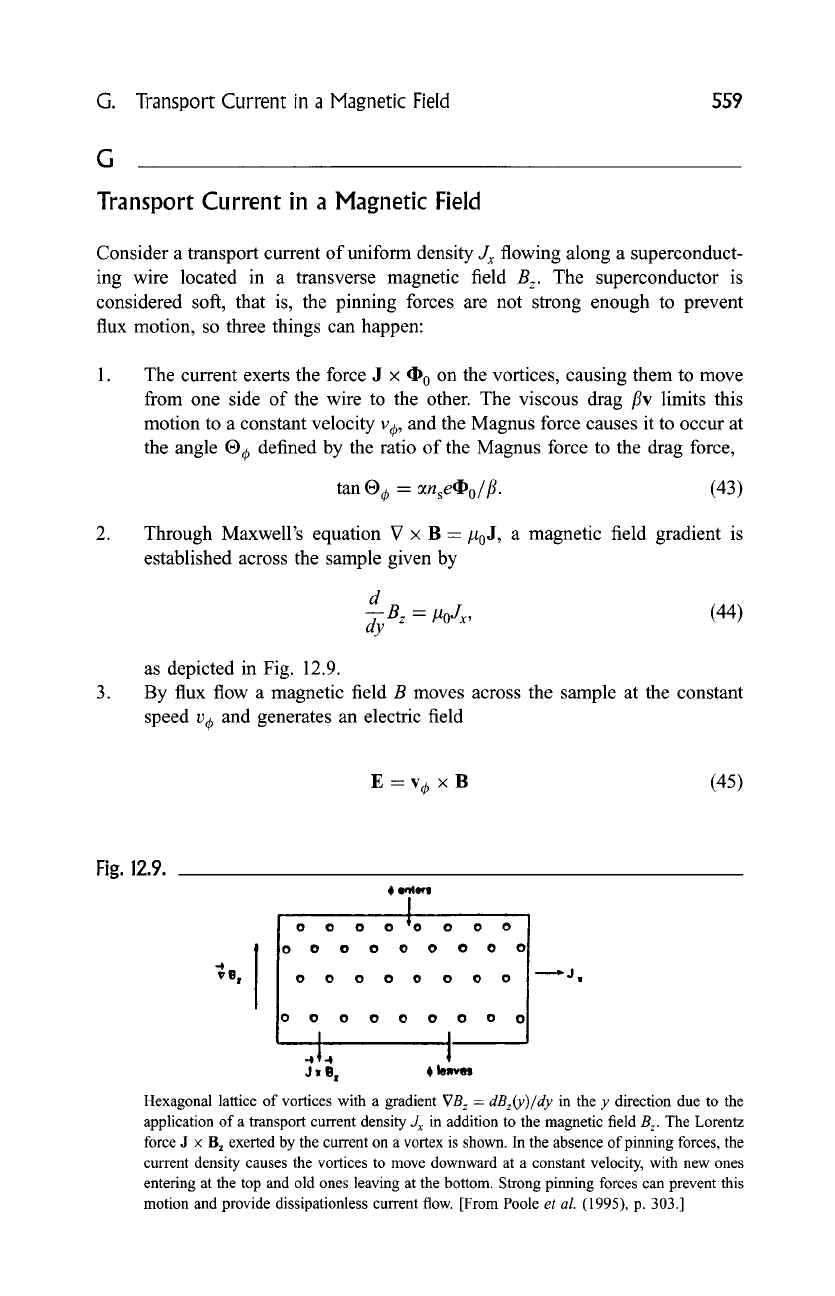
Through Maxwell's equation V x B = #0 J, a magnetic field gradient is

established across the sample given by

d

-- B z = #OJx,

(44)

dy

as depicted in Fig. 12.9.

By flux flow a magnetic field B moves across the sample at the constant

speed v~ and generates an electric field

E - v~ x B (45)

Fig. 12.9.

.4

vgj

6 er~ere

0 0 0 0 I0 0 0 0

0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0 0 --'~J ~

0 0 0 0 0 0 0

'

t

J ~ gt 0 tm.,es

Hexagonal lattice of vortices with a gradient

VB z = dBz(y)ldy

in the y direction due to the

application of a transport current density

Jx

in addition to the magnetic field

B z.

The Lorentz

force J • B z exerted by the current on a vortex is shown. In the absence of pinning forces, the

current density causes the vortices to move downward at a constant velocity, with new ones

entering at the top and old ones leaving at the bottom. Strong pinning forces can prevent this

motion and provide dissipationless current flow. [From Poole

et al.

(1995), p. 303.]

560 Chapter 12: Magnetic Properties

perpendicular to both v~ and B that gives rise to the ohmic loss J. E,

J.E-J.(v~xB),

(46)

and heat dissipation.

H

Magnetic Phase Diagram

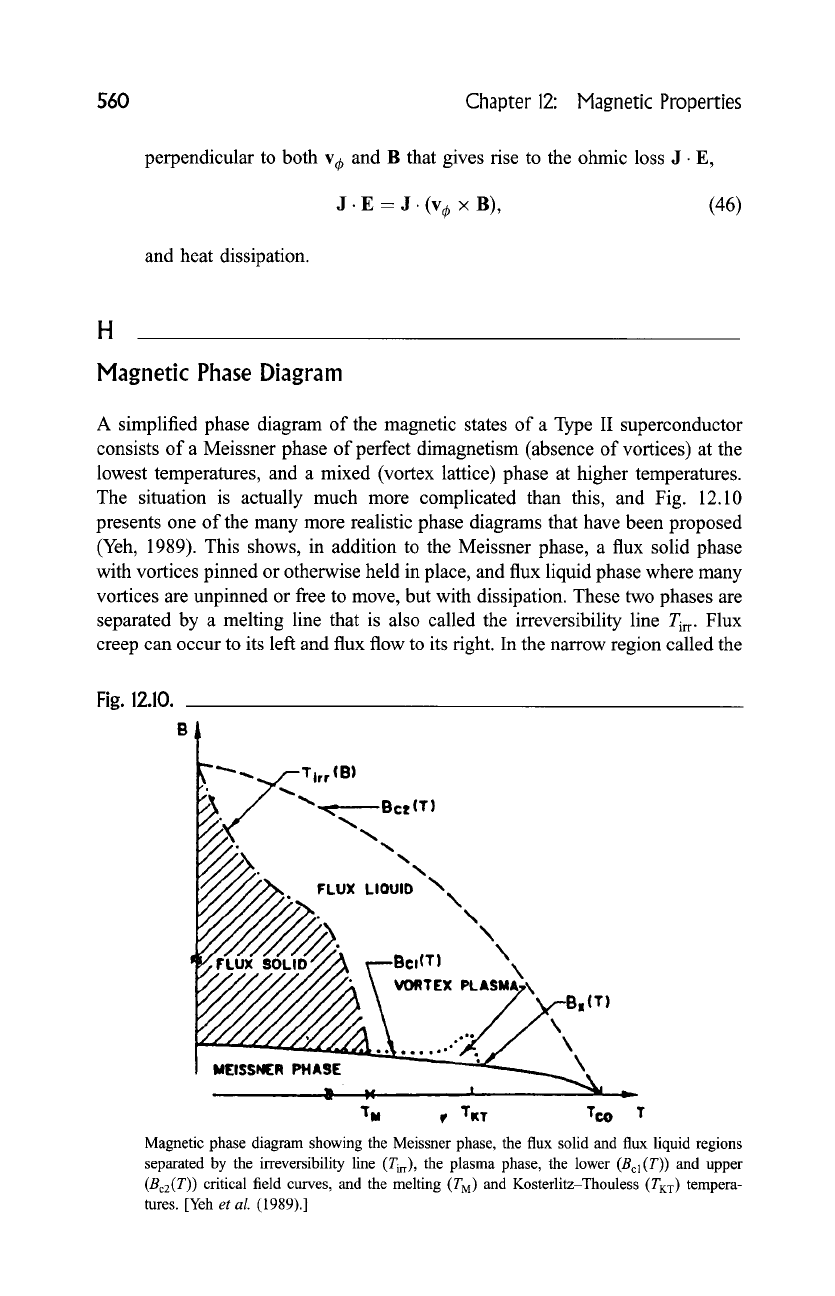
A simplified phase diagram of the magnetic states of a Type II superconductor

consists of a Meissner phase of perfect dimagnetism (absence of vortices) at the

lowest temperatures, and a mixed (vortex lattice) phase at higher temperatures.

The situation is actually much more complicated than this, and Fig. 12.10

presents one of the many more realistic phase diagrams that have been proposed

(Yeh, 1989). This shows, in addition to the Meissner phase, a flux solid phase

with vortices pinned or otherwise held in place, and flux liquid phase where many

vortices are unpinned or free to move, but with dissipation. These two phases are

separated by a melting line that is also called the irreversibility line Tir r. Flux

creep can occur to its left and flux flow to its fight. In the narrow region called the

Fig. 12.10.

|rr

(B)

FLUX SOLID

~',~------Bct (T)

FLUX LIOUID ~

",,

/ Bc

\

VORTEX PLASMA,

MEISSN(R PHASE

e 9 9

Oe~

~-Bx(T)

\

"I'M I, TKT TCO T

Magnetic phase diagram showing the Meissner phase, the flux solid and flux liquid regions

separated by the irreversibility line (Tirr), the plasma phase, the lower (Bcl(T)) and upper

(Bc2(T)) critical field curves, and the melting (TM) and Kosterlitz-Thouless (TKT) tempera-

tures. [Yeh

et al.

(1989).]

I. Ellipsoids in Magnetic Fields

561

plasma phase, thermal fluctuations create short-lived positively and negatively

oriented vortices that are called intrinsic.

Ellipsoids in Magnetic Fields

Until now we have ignored demagnetization effects. We have implicitly treated

the case of a long cylindrical superconductor in an extemal magnetic field applied

along its axis.

When an ellipsoid with a susceptibility Z is placed in a uniform magnetic

field Bap p oriented along one of its principal directions, then its intemal fields

Bin

and Hi. are parallel to the applied field. Their values can be obtained from Eqs.

(1) to (3) with the aid of the demagnetization expression

NBin + (1 - N)laoHin = Bapp, (47)

which relates the internal and applied fields, where N is the demagnetization

factor that satisfies the normalization condition

N a +N b +N c = 1 (48)

for the three principal directions a, b, c. The largest value of N/ is for field

alignment along the shortest principal axis, etc. For the common case of an

ellipsoid of revolution with the c direction selected as the symmetry axis, the

semimajor axes are a - b :/: c, and the demagnetization factors are

Nil -- N c, N_L = N a -- N b, (49)

subject to the normalization condition

Nil + 2N• = 1. (50)

Combining Eqs. (2), (3), and (47) gives

I+X

Bin

--

Bapp 1 + zN (51)

Bin - Bapp//to

1 + zN (52)

M

-

Bapp X

~. (53)

#o 1

+ zN

for the internal fields and the magnetization expressed in terms of the applied

field. We should bear in mind that the susceptibility Z is negative for a super-

conductor, so the denominators in these expressions become small when Z

approaches-1 and N approaches 1.

562 Chapter 12: Magnetic Properties

Experimentalists often express the measured susceptibility

~exp

in terms of

the applied field

Zexp -

#oM/Bapp,

(54)

and this is related to the true susceptibility Z-

M/Hin

as follows:

Zexp --

Z/(1

+

NZ), Z -

Zexp/( 1 - NZexp)- (55)

An oblate ellipsoid, that is, one flattened in the a, b plane, has c < a with

Nil > N• and von Hippel (1954) gives

1 [1

-- 82] 1/2

Nil

=/32 /33

sin -1 e, c < a, (56)

where the oblate eccentricity e is

~; -- [1 --

(c2/a2)] 1/2,

c < a.

(57)

For a prolate ellipsoid, that is, one elongated along its symmetry axis so c > a and

Nil < N• we have

NIl- e2 ~ln _ - 1 , c > a, (58)

where the prolate eccentricity e is

e -[1 -(a2/c2)]

1/2, c > a.

(59)

Figure 12.11 shows how the demagnetization factor depends on the

c/a

ratio, and

Table 12.1 gives expressions for several special cases. The four small correction

factors,

~i (( 1,

included in this table may be deduced from power series

expansions of Eqs. (56) and (58).

Intermediate State of Type ! Superconductor

Until now we have been discussing Type II superconductors. Let us now consider

a Type I superconducting ellipsoid with a demagnetization factor N. It will exist

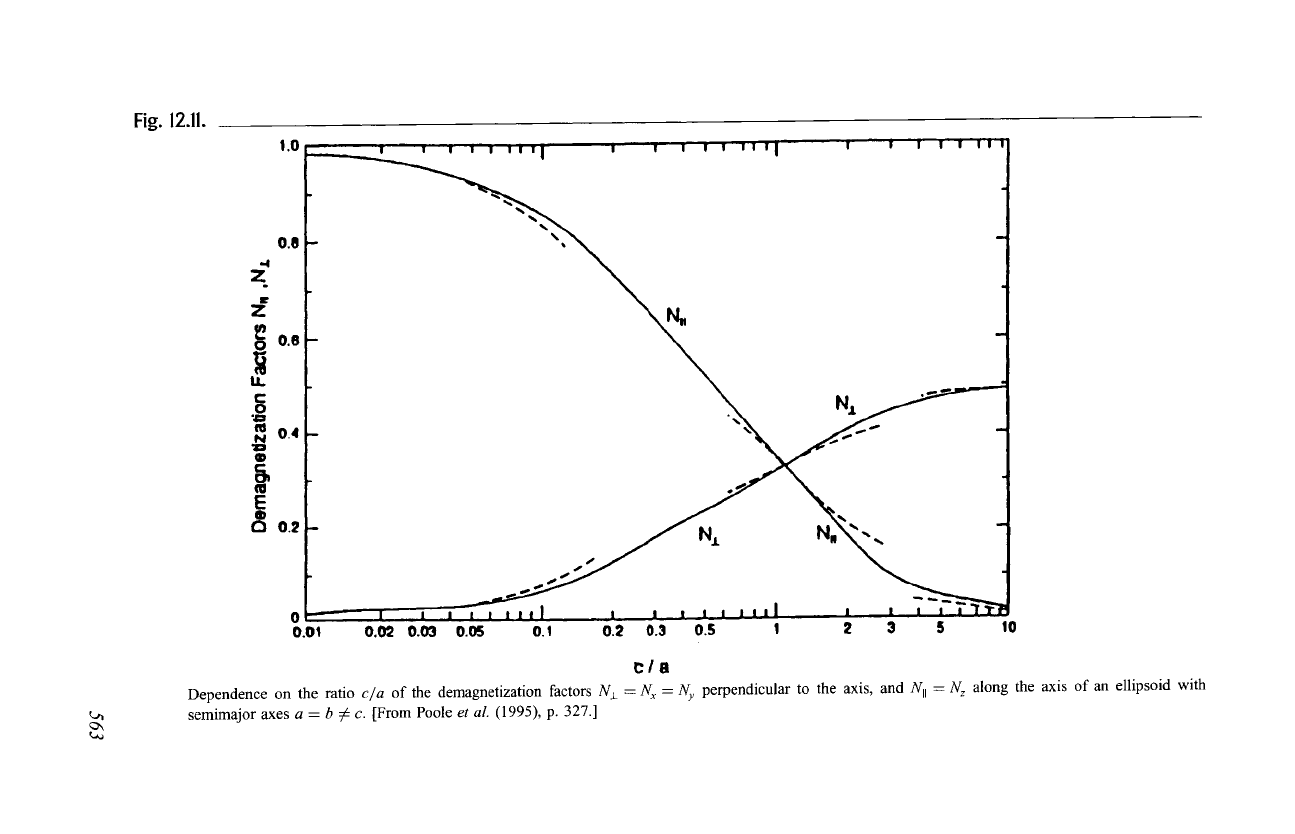
Fig. 12.11.

1.0

_r'"

.'" 9 , w li l|

0.0

,,4

z

=,

z

0 0.6

C

O

aS 0.4

N

~D

Q

g

m

E

O

o o2

J

~J

N~

N.'~-.

,= ,,s

. . , , ,j_,_]_ , ,. . , , ,..i . , _'

+"~,,,

_

o.os o.o2 o.o3 o.os o.t 0.2- o.s O.s t 2 s s to

Dependence on the Patio e/+ of the demagnetization factors Nj_ = N+ -- Ny perpendicular to the axis, and Nit = N+ along the axis of an ellipsoid with

semimajo+ axes + = + :~ e. [Prom Poole

et

+l. C1995), p. 32?.]

564

Chapter 12: Magnetic Properties

Table 12.1

Demagnetizatin factors for ellipsoids of revolution

with semiaxes a = b and c for the cases of a disk

(oblate, c < a), sphere (c = a), and rod (prolate,

c > a) (Poole

et al.,

1995 p. 326).

Shape Condition N• Nil

Disk limit c ~ 0 0

Flat disk c << a 89 61

1

89

Oblate c < a 3

1

Sphere c = a

Prolate c > a 1

+ 163

1

164

Long rod c >> a 2

1

Rod limit c -+ oo

1

--61

1+6 2

1

_

3

~-63

64

0

61 = xc/2a

32 = (4/15)[1 --

c/a]

63 = (4/15)[1 -

a/c]

64 = [1 ln(2c 2/a

2) _

1](a 2/c2).

in a true Meissner state excluding magnetic flux for applied fields less than

(1 -N)B

c

with the characteristics (vide Eqs. (51) to (53))

Bap p <

(1 -

N)B c

(60)

Bin --0 (61)

Hin --

Bapp/(1 - N)# 0

(62)

p0 M

-- -Bap p/(1

- N)

(63)

Z = -1. (64)

At higher applied fields, namely, (1 -N)B

c <_

Bap p < Bc, the material is in the

intermediate state in which it splits into domains of normal material with Z ~ 0

embedded in pure superconducting regions with Z - -1. The boundary separat-

ing normal from superconducting regions has the approximate thickness

dboun d ~ (~ - 2), (65)

and the overall energy density per unit area of this boundary layer is

-- (Bc /21.to)dboun d.

(66)

gbound 2

The domains of normal material have dimensions and separations that are much

greater than dboun d. The fields averaged over these regions of normal, boundary

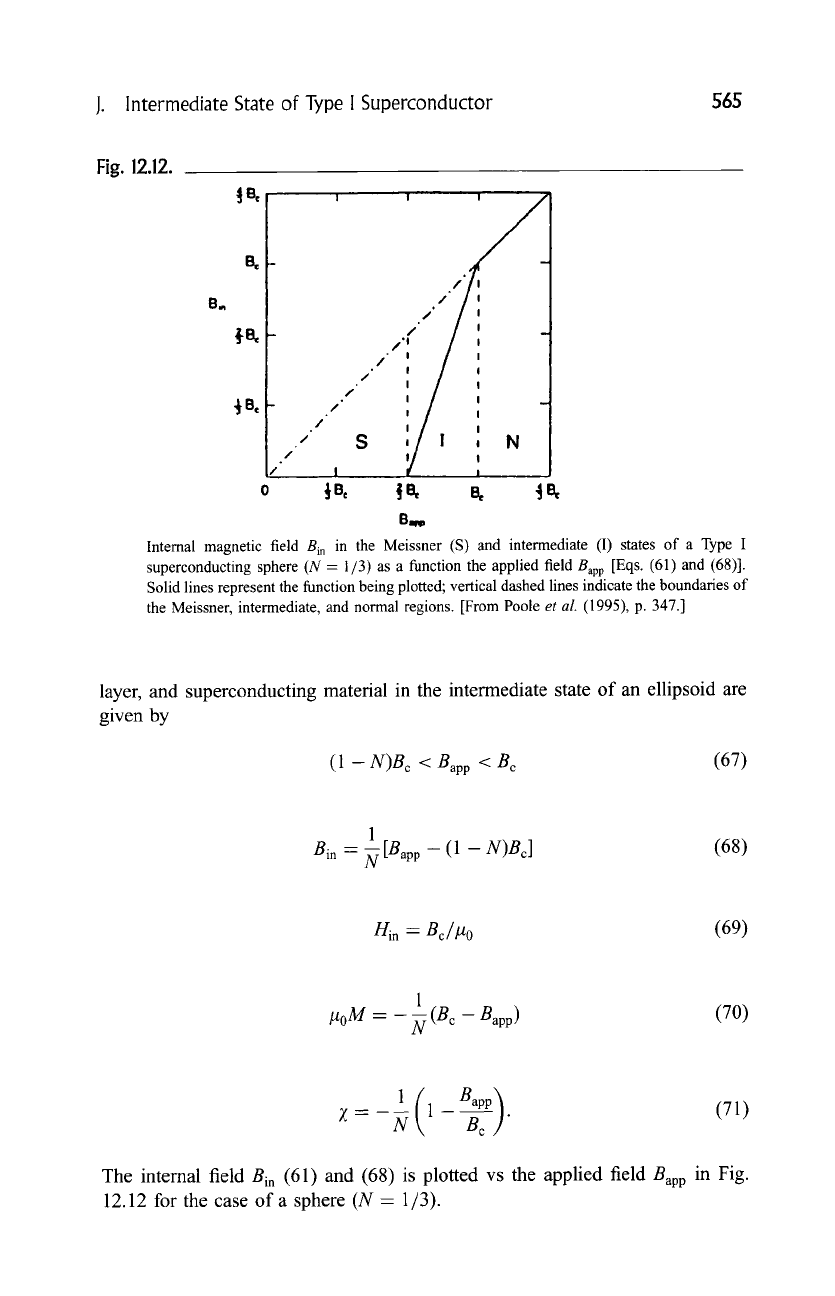
J. Intermediate State of Type I Superconductor

565

Fig. 12.12.

B.

,JB,-

/

0

,

/

f

/

s

!

"/i

/" !

_

/'1

/" I I

! !

I !

I I _

I I

I .. , I

Internal magnetic field Bm in the Meissner (S) and intermediate (I) states of a Type I

superconducting sphere (N = 1/3) as a function the applied field Bap p [Eqs. (61) and (68)].

Solid lines represent the function being plotted; vertical dashed lines indicate the boundaries of

the Meissner, intermediate, and normal regions. [From Poole

et al.

(1995), p. 347.]

layer, and superconducting material in the intermediate state of an ellipsoid are

given by

(1 -N)B c

< Bap p <

B c

(67)

1

Bin -- ~ [Map p -

(1

- N)Bc] (68)

Hin -

Bc/]l 0

(69)

1

p0 M -- - ~ (B c

- Bapp)

(70)

1( Bapp~ (71)

Z--~ 1-Bc/.

The internal field

Bin

(61) and (68) is plotted vs the applied field

Bap p

in Fig.

12.12 for the case of a sphere (N - 1/3).

Poole Ch.P., Jr. Handbook of Superconductivity

Подождите немного. Документ загружается.