Полшков Ю.Н. Курс лекций по экономико-математическому моделированию
Подождите немного. Документ загружается.

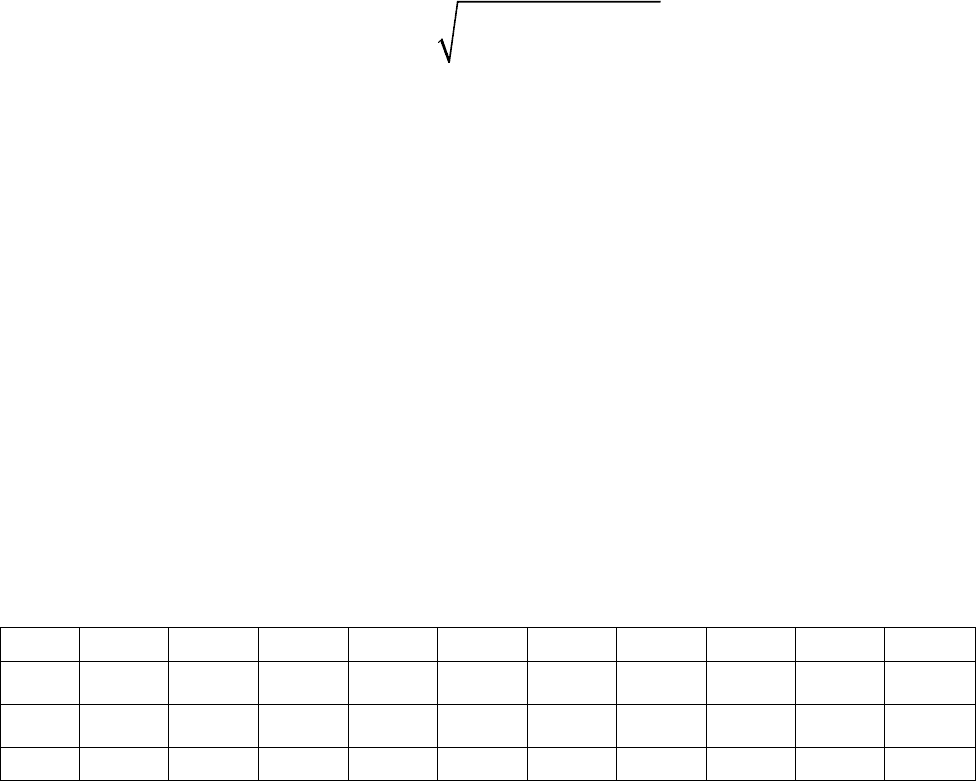
90
(0)
1
(0)
02
(0)
1
...
m
x
Xx
x
⎛⎞
⎜⎟
⎜⎟
⎜⎟
=
⎜⎟
⎜⎟
⎜⎟
⎝⎠
.
Тогда точечный прогноз для среднего значения регрессанта может быть най-
ден по формуле:
y
l
l
/
0
0
YXB
=
⋅ .
Рассчитаем дисперсию прогноза:
(
)
1
22 //
ост 00pr
XXXX
σσ
−
=⋅ .
Извлекая квадратный корень, получаем среднеквадратическую ошибку прогно-
за:
()
1
//
ост 00pr
XXXX
σσ
−
=⋅ .
Доверительный интервал для среднего значения (математического
ожидания) прогноза зависимой переменной имеет вид:
l
()
[
]
l
(
)
00
табл 0 табл
;;
p
rp
Yt k MYYt k
r
α
σα
−⋅≤≤+
σ
⋅.
Доверительный интервал для индивидуального значения прогноза за-
висимой переменной имеет вид:
l
()
l
(
)
00
табл () 0 табл ()
;;
p
ri pri
Yt k YYt k
ασ ασ
−⋅≤≤+⋅
,
где соответствующая стандартная ошибка определяется из формулы:
22
() ост
pr i pr
2
σ
σσ
=+.
3. Продемонстрируем возможности матричного подхода для построения линей-
ных эконометрических моделей. Воспользуемся бывшим ранее примером.
Пример 1. Имеются данные о сменной добыче угля на одного рабочего
(т), мощности пласта
y
1
x
(м) и уровне механизации работ
2
x
(%), характери-
зующие процесс добычи угля в 10 шахтах.
Табл. 1. Данные примера 1
№ 1 2 3 4 5 6 7 8 9 10
1
x
8 11 12 9 8 8 9 9 8 12
2
x
5 8 8 5 7 8 6 4 5 7
y
5 10 10 7 5 6 6 5 6 8
Предполагая, что между переменными , y
1
x
,
2
x
существует линейная за-
висимость, требуется: 1) найти уравнение регрессии по
y
1
x
и
2
x
; 2) с помо-
щью алгоритма пошаговой регрессии построить эконометрическую модель с

91
максимальным числом значимых коэффициентов при уровне значимости 0,05;
3) построить точечный и интервальный прогнозы для при допущении, что
средние показатели по независимым переменным будут превышены на 5%.
y
Решение. Сформируем матрицы данных:
185
1118
112 8
195
187
188
196
194
185
112 7
X
⎛⎞
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
=
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎝⎠
; .
5
10
10
7
5
6
6
5
6
8
Y
⎛⎞
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
=
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎝⎠
1) Расчёты проведём в Microsoft Excel, округляя числа до четвёртого зна-
ка после запятой. Найдём оператор оценивания 1МНК.
l
()
1
//
3,5393
0,8539
0,3670
BXXXY
−
−
⎛⎞
⎜⎟
==
⎜⎟
⎜⎟
⎝⎠
,
Линейное уравнение множественной регрессии имеет вид:
12
3,5393 0,8539 0,3670
x
yx=− + ⋅ + x⋅
,
что совпадает с полученными ранее результатами.
2) Найдём несмещенную оценку дисперсии остатков:
l
()
l
/
/
//
2
496 489,6704
0,9042
117
YY BXY
nm nm
ε
εε
σ
−−
== = =
−− −−
,
где – число наблюдений,
10n = 2m
=
– количество независимых переменных.
Определим ковариационную матрицу оценок параметров эконометриче-
ской модели:
l
()
l
()
2
1
/
3,6351 0, 2925 0,1263
var 0, 2925 0,0486 0,0261
0,1263 0,0261 0,0590
BXX
ε
σ
−
−
−
⎛⎞
⎜⎟
=⋅ =− −
⎜⎟
⎜⎟
−−
⎝⎠
.
Следовательно, квадраты стандартных ошибок равны:
l
()
2
3,6351a
σ
=
;
l
(
)
2
1
0,0486b
σ
=
;
l
(
)
2
2
0, 0590b
σ
=
.

92
Вычислим общую дисперсию результативного признака и остаточную
дисперсию:
()
2
2
1
3, 36
y
yy
n
σ
=−=
∑
;
l
/
//
2
ост
0, 6330
YY BXY
n
σ
−
==
.
Множественный коэффициент детерминации равен:
2
2
ост
2
1 0,8116
y
R
σ
σ
=− = .
Скорректированный множественный коэффициент детерминации:
l
()
()
()()
2
2
2
1
1 0,7578
1
x
yy nm
R
yy n
−−−
=− =
−−
∑
∑
.
Это означает, что дисперсия результативного признака , объясняется на
75,78% влиянием переменных
y
1
x
и
2
x
. Оставшаяся доля дисперсии 24,22% вы-
звана влиянием других, не учтённых в модели, факторов.
Средняя ошибка аппроксимации составляет:
1
100% 10, 2390%
x
yy
A
ny
−
=⋅=
∑
,
что практически соответствует норме.
Множественный коэффициент корреляции и его скорректированное зна-
чение, соответственно, равны:
0,9009R
=
; . Близость к 1 говорит
о тесной связи результативного признака со всем набором исследуемых факто-
ров.
l
0,8705R =
Рассчитаем наблюдаемое значение -критерия Фишера:
F
2
2
1
15,0794
1
Rnm
F
Rm
−−
=⋅ =
−
.
Сравним его с табличным значением при уровне значимости
0, 05
α
= и степе-
нях свободы и :
1
2km==
2
17knm=− −=
(
)
табл
0, 05; 2; 7 4,7374F = . Так
как
(
)
табл 12
;;FF kk
α
> ,
то найденное уравнение регрессии статистически значимо с надёжностью не
менее 95%.
Вычислим фактическое значение
t
-критерия Стьюдента:
l
l
2
1
4,6799
1
Rn m
t
R
−−
==
−
,
которое сравним с табличным значением при уровне значимости 0, 05
α
= и
числе степеней свободы :
17knm=− −=
(
)
табл
0, 05; 7 2,3646t
=
. Так как

93
(
)
табл
;tt k
α
> ,
то множественный коэффициент корреляции статистически значим с надёжно-
стью не менее 95%.
Для проверки значимости коэффициентов регрессии их величины срав-
ниваются с их стандартными ошибками. Определим фактические значения -
критерия Стьюдента:
t
l
()
1
1
1
( ) 3,8726
b
tb
b
σ
==
;
l
()
2
2
2
( ) 1,5108
b
tb
b
σ
==
,
которые затем сравниваются с табличным значением
(
)
табл
0, 05; 7 2,3646t = .
Так как
()
1
табл
() ;tb t k
α
>
,
()
1
табл
() ;tb t k
α
<
,
то оценка коэффициента регрессии статистически значима с надёжностью не
менее 95%, а оценка статистически незначима.
1
b
2
b
Следовательно, независимая переменная
2
x
должна быть исключена из
модели.
Продолжим выполнение алгоритма пошагового регрессионного анализа.
Сформируем матрицы исходных данных:
18
111
112
19
18
18
19
19
18
112
X
⎛⎞
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
=
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎝⎠
; .
5
10
10
7
5
6
6
5
6
8
Y
⎛⎞
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
=
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎝⎠
Найдём оператор оценивания 1МНК.
l
()
1
//
2, 7541
1, 0164
BXXXY
−
−
⎛⎞
==
⎜⎟
⎝⎠
,
Новое уравнение регрессии имеет вид:
1
2, 7541 1,0164
x
yx=− + ⋅ .

94
Несмещенная оценка дисперсии остатков:
l
2
1, 0492
ε
σ
= . Ковариационная
матрица оценок параметров эконометрической модели:
l
()
3,9043 0, 4042
var
0, 4042 0,0430
B
−
⎛⎞
=
⎜⎟
−
⎝⎠
.
Квадраты стандартных ошибок равны:
l
(
)
2
3,9043a
σ
= ;
l
()
2
1
0,0430b
σ
=
.
Общая дисперсия результативного признака и остаточная дисперсия:
; . Множественный коэффициент детерминации:
.
2
3, 36
y
σ
=
2
ост
0,8393
σ
=
2
0, 7502R =
Скорректированный множественный коэффициент детерминации:
. Это означает, что дисперсия результативного признака , объ-
ясняется на 71,90% (ранее было 75,78%) влиянием переменной
l
2
0, 7190R =
y
1
x
. Оставшаяся
доля дисперсии 28,10% вызвана влиянием других, не учтённых в модели, фак-
торов.
Средняя ошибка аппроксимации
11,8283%A = , что несколько больше
нормы. Множественный коэффициент корреляции и его скорректированное
значение, соответственно, равны:
0,8661R
=
; . Близость к 1 гово-
рит о достаточно тесной связи результативного признака с фактором
l
0,8479R =
1
x
.
Наблюдаемое значение -критерия Фишера:
F 24,025F
=
. Сравним его с
табличным значением при уровне значимости
0, 05
α
=
и степенях свободы
и :
1
1km==
2
18knm=− −=
(
)
табл
0,05; 1; 8 5,3177F
=
. Так как
(
)
табл 12
;;FF kk
α
> ,
то найденное уравнение регрессии статистически значимо с надёжностью не
менее 95%.
Фактическое значение -критерия Стьюдента
t 4,5240t
=
сравним с таб-
личным значением при уровне значимости
0, 05
α
=
и числе степеней свободы
:
18knm=− −=
()
табл
0, 05; 8 2, 3060t
=
. Так как
(
)
табл
;tt k
α
> ,
то множественный коэффициент корреляции статистически значим с надёжно-
стью не менее 95%.
Проверим значимость оставшегося коэффициента регрессии . Опреде-
лим фактические значения -критерия Стьюдента:
1
b
t
( ) 1,3938ta=−
;
. Так как
1
( ) 4,9015tb =
()
1
табл
() ;tb t k
α
>
,

95
то оценка коэффициента регрессии статистически значима с надёжностью не
менее 95%.
1
b
Итак, алгоритм пошагового регрессионного анализа привёл нас к эконо-
метрической модели с максимальным числом значимых коэффициентов регрес-
сии:
1
2, 7541 1,0164
x
yx=− + ⋅ .
По соответствующим формулам найдём доверительные интервалы оце-
нок параметров, входящих в модель:
()
l
(
)
()
l
()
табл табл
;;at k a aat k a
ασ ασ
−⋅≤≤+⋅;
;
7,3106 1,8024a−≤≤
()
l
(
)
()
l
()
111
табл 1 табл
;;bt k b bbt k b
ασ ασ
−⋅≤≤+⋅
1
;
1
0,5382 1, 4946b
≤
≤ .
3) Построим точечный и интервальный прогнозы для при допущении,
что средние показатели по
y
1
x
и
2
x
будут превышены на 5%.
Так как
1
9, 4x = , то предполагаемое значение:
(0)
11
(1 0, 05) 9, 4 1, 05 9,87xx=+ =⋅ = (м).
Вектор предполагаемых значений:
0
1
9,87
X
⎛⎞
=
⎜⎟
⎝⎠
.
Точечный прогноз для среднего значения регрессанта :
y
l
l
/
0
0
7, 2777YXB=⋅=
(т).
Дисперсия прогноза:
(
)
1
22 //
ост 00
0,0915
pr
XXXX
σσ
−
=⋅ = .
Среднеквадратическая ошибка прогноза:
0,3026
pr
σ
=
.
Доверительный интервал для среднего значения (математического ожи-
дания) прогноза зависимой переменной:
l
()
[
]
l
(
)
00
табл 0 табл
;;
p
rp
Yt k MYYt k
r
α
σα
−⋅≤≤+
σ
⋅;
[
]
0
7,0666 7,9754MY
≤
≤ .
Доверительный интервал для индивидуального значения прогноза:
l
()
l
(
)
00
табл () 0 табл ()
;;
p
ri pri
Yt k YYt k
ασ ασ
−⋅≤≤+⋅;
0
5,0528 9,5026Y
≤
≤ .
где соответствующая стандартная ошибка определяется из формулы:
222
() ост
0,8393 0,0915 0,9308
pr i pr
σσσ
=+= + =
.
Решение окончено.
96
Лекция 7
МУЛЬТИКОЛЛИНЕАРНОСТЬ
План лекции
1. Понятие мультиколлинеарности.
2. Алгоритм Фаррара-Глобера.
3. Практический пример исследования мультиколлинеарности.
1. Мы продолжаем изучать линейные модели множественной регрессии. На-
помним, что их спецификация является следующей:
11 2 2
...
iiimim
yabxbx bx
i
ε
=+ + ++ +,
где – номер наблюдения.
1,...,i= n
m
В формулировке теоремы Гаусса-Маркова предполагалось выполнение
гипотезы 2: а) числовые значения независимых переменных
12
, ,...,
ii i
x
xx яв-
ляются детерминированными (не случайными) величинами; б) векторы
1
2
...
j
j
j
nj
x
x
x
x
⎛⎞
⎜⎟
⎜⎟
=
⎜⎟
⎜⎟
⎜⎟
⎝⎠
, 1,...,jm
=
линейно независимы в пространстве .
n
R
Нарушение условия линейной независимости векторов
j
x
приводит к
нежелательному явлению, называемому мультиколлинеарностью.
Мультиколлинеарность означает существование тесной линейной зави-
симости, или сильной корреляции, между двумя или более объясняющими пе-
ременными.
Она негативно влияет на количественные характеристики эконометриче-
ской модели, или делает ее построение вообще невозможным.
Информацию о парной зависимости может дать матрица коэффициен-
тов парной корреляции между объясняющими переменными:
11 1 2 13 1
21 2 2 23 2
31 3 2 33 3
123
(, ) (, ) (, ) ... (, )
(,) (, ) (,)... (, )
(,) (, ) (,) ... (, )
... ... ... ... ...
(,) (,) (,)... (, )
m
m
m
mm m m
rx x rx x rx x rx x
rx x rx x rx x rx x
r rxx rxx rxx rxx
rx x rx x rx x rx x
⎛⎞
⎜⎟
⎜⎟
⎜⎟
=
⎜⎟
⎜⎟
⎜⎟
⎝⎠
m
.
Начальная проверка предусматривает нахождение определителя (детер-
минанта) матрицы , который называется детерминантом корреляции и обо-
значается . Числовые значения детерминанта корреляции удовлетворяют
условию:
r
det( )r
[
]
det( ) 0,1r ∈ .

97
Если , то существует полная мультиколлинеарность, а если
, то мультиколлинеарность отсутствует. Чем ближе к нулю,
тем уверенней можно утверждать, что между объясняющими переменными су-
ществует мультиколлинеарность.
det( ) 0r =
det( ) 1r = det( )r
2. Наиболее полно исследовать мультиколлинеарность можно при помощи ал-
горитма Фаррара–Глобера.
Опишем этот алгоритм.
1) Стандартизация (нормализация) векторов независимых переменных
12
, ,...,
m
x
xx:
*
()
k
ik
ik
k
x
x
x
x
σ
−
= ,
где – число наблюдений
n (1,in= ); – число объясняющих переменных m
(1,)km= ;
x
k
– выборочное среднее -й объясняющей переменной; k
()
k
x
σ
–
выборочное среднее квадратическое отклонение -й объясняющей перемен-
ной.
k
2) Нахождение корреляционной матрицы:
*/ *
1
rXX
n
=
,
где – матрица стандартизированных независимых переменных.
*
X
3) Определение критерия
2
χ
(“хи”-квадрат):
[]
2
1
1(25)lndet(
6
nm
χ
⎡⎤
=− − − +
⎢⎥
⎣⎦
)r
.
Фактическое значение этого критерия
2
χ
сравнивается с табличным зна-
чением
2
t
χ
при
1
(1)
2
m+ m
степенях свободы и уровне значимости
α
. Если
2
t
2
χ
χ
> , то в массиве объясняющих переменных существует мультиколлине-
арность.
4)Определение обратной матрицы:
1
Cr
−
=
.
5) Вычисление -критериев:
F
1
(1)
kkk
nm
Fc
m
−
−
=−
,
где – диагональные элементы матрицы . Фактические значения критериев
сравниваются с табличным при и
kk
c
C
t
F m 1nm
−
− степенях свободы и уровне
значимости
α
. Если , то соответствующая -тая независимая перемен-
ная мультиколлинеарна с другими.
k
FF>
t
k
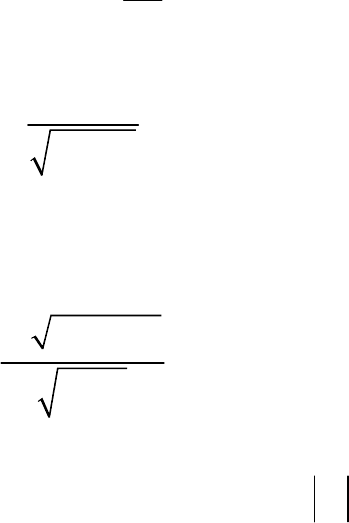
98
Коэффициент детерминации для каждой переменной
[]
2
1
() 1
k
kk
Rx
c
=−
.
6) Нахождение частных коэффициентов корреляции:
kj
kj
kk jj
c
r
cc
−
=
⋅
,
где – элемент матрицы , содержащийся в -ой строке и -ом столбце;
и
kj
c C k j
kk
c
j
j
c – диагональные элементы матрицы C .
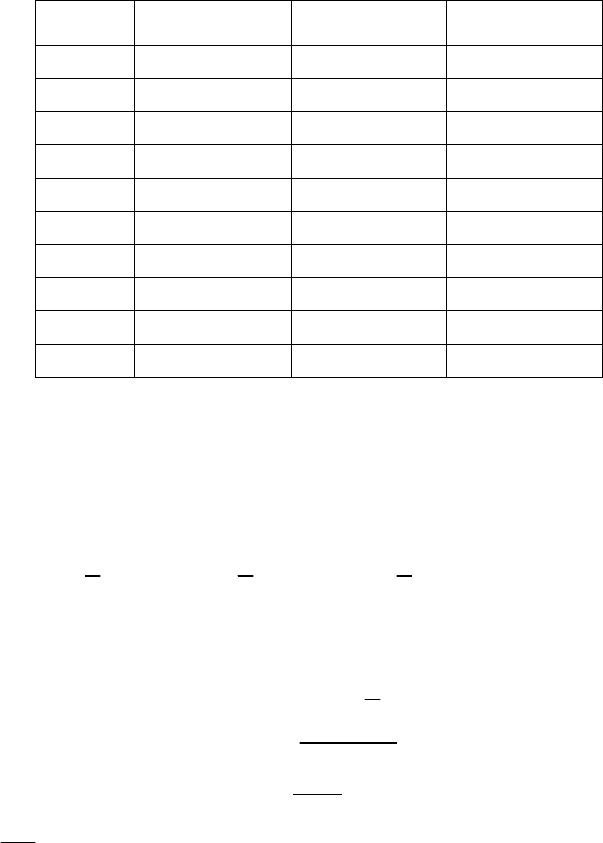
7) Вычисление
t-критериев:
2
1
1
kj
kj
kj
rnm
t
r
−
−
=
−
.
Фактические значения критериев сравниваются с табличным при
степенях свободы и уровне значимости
kj
t
T
t
1nm−−
α
. Если
kj T
t> t, то между
независимыми переменными
k
x
и
j
x
существует мультиколлинеарность.
Для того, чтобы избавиться от мультиколлинеарности в эконометриче-
ской модели, можно исключить из нее одну из переменных мультиколлинеар-
ной пары
k
x
и
j
x
. Удалить следует переменную с большим значением -
критерия, т.к. она больше влияет на общую мультиколлинеарность модели. Од-
нако этот шаг не должен противоречить экономическому смыслу задачи.
F
Заметим, что имеются и другие способы устранения мультиколлинеарно-
сти. Среди них: а) взять не сами значения переменных, а их отклонения от
средней; б) вместо абсолютных значений факторов взять относительные; в)
стандартизировать объясняющие переменные и т. д.
При наличии мультиколлинеарности переменных необходимо обращать
внимание на спецификацию модели. Иногда замена одной функции на другую
дает возможность избежать мультиколлинеарности.
3. Рассмотрим применение алгоритма Фаррара–Глобера на практике.
Пример 1. На производительность труда однотипных малых предпри-
ятий влияет ряд факторов, среди которых: удельный вес рабочих на предпри-
ятии
1
x
; премии и др. вознаграждения на одного работника
2
x
(ден. ед.); обора-
чиваемость нормируемых оборотных средств
3
x
(дни). Исследовать на мульти-
коллинеарность переменные
1
x
,
2
x
,
3
x
. При наличии мультиколлинеарности
предложить меры по её устранению. Статистические данные по десяти пред-
приятиям приведены в табл. 1.
99
Табл. 1. Данные по десяти предприятиям
№
1
x
2
x
3
x
1 0,68 0,42 25,68
2 0,74 0,05 18,13
3 0,66 0,29 25,74
4 0,72 0,48 21,21
5 0,68 0,41 22,97
6 0,77 0,62 16,38
7 0,78 0,56 13,21
8 0,78 1,76 14,48
9 0,81 1,31 13,38
10 0,79 0,45 13,69
Решение. Исследуем мультиколлинеарность в массиве независимых пе-
ременных при помощи алгоритма Фаррара–Глобера. Расчёты проведём в
Microsoft Excel, округляя числа до четвёртого знака после запятой.
1) Для стандартизации (нормализации) векторов независимых перемен-
ных рассчитаем выборочные средние и средние квадратические отклонения:
1
0,741x = ;
2
0,635x = ;
3
18, 487x = ;
1
( ) 0,0505x
σ
=
;
2
( ) 0, 4841x
σ
=
;
3
( ) 4,7898x
σ
=
.
Стандартизируем данные по формуле:
*
()
k
ik
ik
k
x
x
x
x
σ
−
= ,
где – число наблюдений
10n = ( 1,10)i = ; 3m
=
– число объясняющих пере-
менных
(1,3k = ). Матрица стандартизированных данных:
*
1, 2082 0, 4441 1,5017
0, 0198 1, 2084 0,0745
1, 6044 0,7127 1,5143
0, 4159 0,3202 0,5685
1, 2082 0, 4648 0,9360
0,5744 0,0310 0, 4399
0, 7725 0,1549 1,1017
0, 7725 2,3239 0,8366
1,3667 1,3944 1, 0662
0,9705 0,3822 1,00
X
−−
−−−
−−
−−
−−
=
−−
−−
−
−
−−15
⎛⎞
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎝⎠
.
