Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач
Подождите немного. Документ загружается.


§
1.6]
СОБСТВЕННО
И
подлинно
ЭФФЕКТИВНЫЕ
РЕШЕНИЯ
51
для
которого
будет
справедливо
неравенство
(2).
Поэтому
смысл
приведенного
определения
ааключается
в
требова
нии
существования
числа
е,
для
которого
при
указанных
условиях
выполняется
(З).
Решения,
которым
соответствуют
собственно
эффек
тивные
оценки,
также
называются
собственно
эффею'пв
ными,
или
оптимальными
по
Джоффриону.
Множество
всех
таких
решений
(оценок)
будем
обозначать
через
Gj(X)
(С(У»).
Так,
в
примере
1
множество
С(У)
-
это
верхняя
ветвь
параболы
у,
=
-(У2)2
(без
вершины
уО).
При
м
е
р
2.
Наилучшая
по
:2::
ОЦeIша
уО
Е
У
являет
ся
собственно
эффективной,
так
как
уО
:?у
для
всех
у
Е
У
II
неравенство
(1)
не
выполняется.
Следовательно,
реше
нпе,
обращающее
в
максимум
одновременно
I\.аждыЙ
из
критериев
/"
/2,
...
,
/т
собственно
эффеRТИВНО.
В
част
ности,
в
однокритериальных
задачах
любое
оптимальное
решение
и
собственно
эффективно.
При
м
е
р
3.
Если
множество
У
конечно,
то
всю{ая
эффективная
оценка
является
и
собственно
эффеI<ТIlВНОЙ.
Действительно,
в
случае
конечного
У
множество
Р( У)
внешне
устойчиво
(§
1.4).
Следовательно,
если
эффектив
ная
оцеlJка
уО
единственна,
то
она
является
наилучшей
по
б,
и
потому
собственно
эффеI{ТИВНОЙ
(пример
2).
Если
же
Р(
У)
содержит
более
одной
оцеНI<И,
то
искомое
поло
жительное
число
е
можно
задать
равен.ствои
{
Y'-Y~
\
е
=
тах
~
~
у
Е
У,
Yj -
У]
i.,
jEM,t
i
=1=
j;
Итак,
если
У
конечно
(а
для
этого
достаточно
конеч
ности
множества
Х), то
понятия
эффеI<ТИВНОСТИ
и
собст
венной
эффективности
равносильны.
ЭффеI<тивная
оценка,
не
являющаяся
собственно
эф
феI<ТИВНОЙ,
называется
nесобствеnnо
эффе/'i,тuвuоЙ.
Ана
логичная
терминология
вводится
и
для
решений.
В
соответствии
с
определением,
если
уО
несобствепно
эффективна,
то
это
означает
следующее:
для
любого
сколь
угодно
большого
е
>
о
найдутся
такие
i
Е
М,
У
Е
У,
удовлетворяющие
(1),
что
для
всякого
j,
для
IЮТQ-
4*

52
ОСНОВНЫЕ
понятия
И
ОПРЕДЕЛЕНИЯ
[ГЛ.
1
рого
выполняется
(2),
будет
справедливо
неравенство
(Yi -
y~)/(yY
- Yj) >
О.
(4)
Возьмем
бесконечно
возрастающую
последователь
ность
положительных
чисел
{ОТ}:
lim
ОТ
= +
00.
ЕСЛIl
у
О
т-+оо
несобственно
эффективна,
то
наждому
r =
1,
2,
.,.
можно
поставить
в
соответствие
номер
i(r),
для
которого
при
не
котором
У
Е
У
справедливо
неравенство
(1).
Тан
как
множество
М
конечно,
то
в
последовательности
{i(r)}
по
крайней
мере
один
номер
i
повторяется беснонечное
чиС
ло
раз.
Пусть
этому
номеру
соответствует
последователь
ность
индексов
{rJ.
Таним
образом,
для любого
члена
бесконечно
возрастающей
последовательности
{ОП
I
су-
ществует
тюйя
оценка
У
Е
У,
у
которой
Yi
>
У?
и
при
любом
j,
удовлетворяющем
(2),
выполняется
неравенст
во
(4)
с
е
=
OTl'
Изложенное
означает,
что
переходом
от
несобственно
эффективного
решения
к
некоторому
другому
можно
обеспечить
приращение
по
крайней
мере
по
одному
част
ному
критерию
за
счет
потерь
более
высокого
порядна
малости
по
всем
тем
критериям,
значения
которых
умень
шатся.
Иными
словами,
несобственно
эффективные
реше
ния
в
указанном
смысле
аномальны
(неустойчивы)
.
При
м
е
ч
а
н
и
е
1.
Кан
уже
уназывалось,
понятия
собственно
эффективных
оценок
и
решений
не
имеет
смысла
вводить
в
тех
случаях,
когда
одни
критерии
не
сравненно
важнее
других.
Задачи,
в
ноторых
критерии
упорядочены
по
важности
(и
перенумерованы)
так,
что
каждый
предыдущий
несравненно
важнее,
чем
все
пос
ледующие,
называются
леНСИIюграфичеснимп
задачами
оптимизации,
так
как
в
таких
задачах
отношение
нестро
гого
предпочтения
является
леIl:спнографическим
поряд
I<OM
;;;:::
lex.
Этот
ПОРЯДОI{
задается
следующим
образом:
У;;;:::
lex
y',
когда
выполнено
одно
из
условий:
I
1)
Yl>Yl;
I ,
2)
Уl
=
Уl,
У2>
У2;
I
т)
Yi
= Yi,
I
Ут>Ут;
т
+
1)
у
=
у'.

§
1.6]
СОБСТВЕННО
И
ПОДЛИННО
ЭФФЕНТИВНЫЕ
РЕШЕНИЯ
53
отношение
~lex,
являющееся
полным,
упорядочивает
оценю!
подобно
тому,
нан
располагаются
слова
в
словаре,
II
этим
объясняется
происхождение
прилагательного
«леI\СИI\ографичесниЙ».
Из
определения
видно,
что
в
лен
СIIкографичеСI\ОЙ
задаче
следует
добиваться
сноль
угодно
малого
при
ращения
более
важного
I\ритерия
за
счет
СI\ОЛЬ
угОДНО
больших
потерь
по
всем
остальным,'
менее
важ
ным
I\ритериям.
Именно
поэтому
ленсикографичесни
оптимальная
(наилучшая
но
б;lех)
оценна
не
обязана
быть
собственно
эффентивной,
хотя,
нан
лешо
убедиться,
она
обязательно
является
эффентивноЙ.
Тан,
в
примере
1
(рис.
12)
оценна
уО
леI\синографичесни
оптимальна
и
эф
mективна,
но
несобственно.
л
ЛеRсикографичеСI\ие
задачи
оптимизации
обстоятельно
рассматриваются
в
[85].
2.
В
§ 4
было
уназано,
что
задача
многокритериальной
оптимизации
является
специальным
случаем
задачи
опти
мизации
относительно
I\OHyca.
Однако
понятие
собствен
ной
эффен.тивности
(по
Джоффриону)
существенно
использует
<<Координатный»
харантер
отношения
~
и
по
этому
на
более
общий
случай
оптимизации
относительно
нонуса
прямо
не
переносится.
В
связи
с
этим
БорвеЙНОl\l
[124]
было
предложено
общее
определение
собственной
эффективности,
ноторое
мы
сформулируем
здесь
примени
тельно
н
многокритериальной
задаче
оптимизации.
Для
этого
понадобится
понятие
касательного
конуса.
Касательnым
,,"опусом
Т(А,
уО)
но
множеству
А
s:;
Ет
в
точке
уО
Е
А
называется
множество
всех
венторов
из
Ет,
Iюторые
ЯВЛЯЮтся
предельными
точками
вида
w =
=
Нт
t
r
(уТ
-
уО)l
где
{fт}
-
последовательность
неотрица-
Т
.....
оо
тельных
чисел,
а
{ут}
-
последовательность
точек
из
А,
Сходящаяся
н
уО.
На
рис.
13
представлены
касательные
конусы
но
мно
жеству
А
с
Е2
В
трех
его
граничных
точнах.
Заметим,
что
Для
внутренней
точки
множества
А
касательным
кону
сом
является
все
пространство
Ет.
Касательный
нонус
т
(А,
уО)
представляет
один
из
видов
аппроксимации
мно
Жества
А
в
ТОЧRе
уО.
Нетрудно
проверить,
что
касатель
Ный
конус
действительр:о
является
конусом
с
вершиной
в
lIачале
I\оординат,
и
притом
заМRНУТЫМ.

54
ОСНОВНЫЕ
понятия
И
ОПРЕДЕЛЕНИЯ
[ГЛ.
1
Теперь
можно
сформулировать
определение
собствен
ной
эффективности
по
Борвейну,
которую
будем
называть
подлинной
эффективностью
(при
этом
полагаем
У
=
Ет).
Оценка
уО
е
у
называется
подлинно
эффе1'iтивной,
или
оптимальной
по
Ворвейну,
если
она
эффеКТИВIIa
и
т
(У
*1
уО)
n
E~
=
{O(т)}JJ
(5)
где
У*
=
У
-E~
=
(ZE
Em!z
=
У
-е,
УЕ
У,
еЕ
E~l.
(6)
Решения,
оценки
которых
подлинно
эффективны,
таи
же
называются
подлинно
эффе1'iтивным,и.
:Множество
всех
уl
Рис.
13.
таких
решений
(оценок)
будем
обозначать
через
В,(Х)
и
(в(у)).
Согласно
определепию
подлинной
эффек
тивности
В(У)
!с
Р(У)
И
В/(Х}
!с
Р,(Х}.
При
м
е
р
4.
Для
примера
1
У:«
=
У
U
{у
Е
Е
2
1
Уl
:::;
<:
О,
У2
<:
О}.
Здесь
каждая
эффективная
оцеIша,
кроме
уО,
подлинно
эффективна
(так
что
в(у)
с
Р(У)).
Т
е
о
р
е
м
а
1.
Собственно
эффеnтивная
оценnа
явля
ется
и
nодлиН1l0
эффе1'iтивноЙ.
ДонаЗllтельство.
Пусть
уОеС(У),
но
уоФв(у),
т. е.
существует
вектор
а
Е
Т
(У
*,
уО),
все
компоненты
иоторого
неотрицательны
и
по
крайней
мере
одна,
ска
жем
al,
ПОЛОЖlпеЛЪНll.

§
1.6]
СОБСТВЕННО
и
ПОДЛИННО
ЗФФЕ!<ТИ:ВНЬ!Е
РЕШЕНйil
55
Пусть
tT(y'
-
Ь'
-
уО)
-+
а,
где
ь
'
Е
Е";,
t
r
>-
О,
у'
_ь
т
__
-+
уО,
уТ
Е
У.
Поскольку
множество
м=
конечно,
то,
при
необходимости
перейдя
к
подпоследовательности,
можно
считать,
что
множество
М
=
{i
EMly~
<уу}
постоянно
для
всех
r
(оно
непусто,
так
как
уО
Е
Р(У».
Кроме
того,
так
как
аl
>
О,
то
без
ограничения
общности
все
числа
t.
можно
считать
положительными.
Возьмем
произвольное
е>
о.
Тогда
для
достаточно
большого
числа
N
при
любом
r
~
N
будут
справедливы
неравенства
y~
-
уу
>azl2
t
r
,
Yi
-
УУ
'2:.-а
z
2/fJt
r
,
i =
1,
21
.•.
,
т;
i
=1=
l.
Поэтому
для
каждого
t
Е
ii
о
<
Y~
-
yr~az/2etr.
Следовательно,
для
каждого
r
~
N
и
любого
i
Е
М
Vz-
У?
2a
z
8t
r
--::--::-
>
--
=
е
УУ
-
У{
=
:alt
r
,;
а
это
противоречит
у
О
Е
С(
У).
•
Теорема
1
показывает,
что
С(У)
s;;
В(У)
и
С,(Х)
s=
<;;;;,
В,(Х).
В
примере
1
несобственно
эффективная
оценка
уО
не
является
и
подлинпо
эффективной,
так
что
С(
У)
=
В(
У).
Однако
возможно
и
строгое
Вlшючение
С(У)
сВ(У).
Пример
5.
Y={yEE
2
IY2=1IYt,
Yt>O}.
Здесь
каж
дая
оценка
эффективна
и,
очевидно,
подлинно
эффектив
на
(таи
что
У
=
Р(
У)
=
В(
У»,
но
не
является
собственно
эффеЮI1ВНОЙ
(G
(У)
=
!2J).
Действительно,
для
у и
у'
=
([,
1/0,
где
t >
Yt,
получаем
t
lim Y
1
-
Y~
= +
00.
t ...
oo
У
2
-У
2
'
Следует
отметить,
что
переход
из
произвольной
ТОЧI{И
У
в
достаточно
близкую
точку
у
+!:J.y
дает
уменьшение
и
увеличение
Rритериев
одинакового
норядка
малости.

58
ОСНОВНЫЕ
ПОНЯтИЯ
И
ОПРЕДЕЛЕНИЯ
(ГЛ.
t
Этот
пример
подводит
R
выводу
О
том,
что
попятие
собственной
эффеRТИВПОСТИ
излишне
«жесткое)):
опо
«вы
браковывает})
и
такие
эффективные
решения,
ноторые
вполне
могут
(шретендоваты)
на
оптимальные.
Поэтому
определение
Борвейна
представляет
и
самостоятельный
Coocl11lJ{!III/(j!l
,J~~{!/(mlldllocmb
(олmlll'fолЫ/осmь
по
I/ЖОf{J~РIIOll!l
)
ЛоiJЛllIIН(J!I
Jf/Jf/Jf!I(mшJltосmь
(Оn!1ll1/'fОЛbllосmь
по
50pDeliHY)
слоОilJl
.Jf/Jf/J{!/(mlldIlflCmb
(t:.IIUOOil
олmlll'lO//ьносmь
IЮ
Пареmo,
опmШfольнatmь
по
C.IItUmeP!l)
Рис.
14.
интерес
для
l\шогокритериаль
ных
задач
оптимизации.
3.
Выше
были
введены
по
нятия
эффективности
неСIЮЛЬ
ких
типов
и
установлена
опре
деленная
взаимосвязь
между
ними,
схематически
представ
ленная
на
рис.
14.
Этой
схеме
соответствуют
следующие
ВRЛЮ
ченпя
для
множеств
оцепок
и
решений,
эффективных
в раз
личных
смыслах:
С(
У)
s=
В(
У)
s=
Р(
У)
s=
S(
У),
(7)
Gt(X)
s=
В/Х)
s=
Р/(Х)
s=
S/(X).
Примеры,
приведенные
в
этом
и
предыдущих
параграфах,
показывают,
что
наждое
из
этих
ВIшючений,
вообще
гово
ря,
строгое.
В
связи
с
этим
большой
интерес
представляет
вопрос
о
том,
при
каких
условиях
(в
каких
случаях)
понятия
эффеI<ТИВНОСТИ
различного
типа
Оl{азывarотся
ЭIшивалент
пыми,
а
множества
соответствующих
оценон
и
решеЮIЙ
равными.
Это
объясняется
тем,
что
анализ
условий
совпа
дения
решений,
эффективных
в
различных
смыслах,
позволяет
оценить
степень
взаимной
близости
понятий
эффективности
разных
типов,
а
также
дает
возможность
прямого
переноса
того
или
иного
результата,
полученного
для
эффентивных
решений
одного
типа,
на
другой.
В
примере
3
было
показано,
что
для
задач
с
нонечпым
множеством допустимых
решений
понятия
эффективности
и
собственной
эффентивности,
а
значит,
и
подлинной
эф
фективности
совпадают.
В
дальнейших
главах
исследова
ние
поставленного
вопроса
будет
продолжено.
Здесь
мы
докажем
лишь
одно
утверждение,
I\OTopoe
понадобится
в
медующей
шаве
(см.,
например,
[4,
77J).

§ 1.7]
ЭФФЕНТИВНЫЕ
ПОСЛЕДОВАТЕЛЬНОСТИ
57
т
е
о
р
е
м
а
2.
Если
.множество
Х
выnуnло,
а
веnтор
фунnцuл
1
строго
nвазuвогнута
*),
то
Sj(X) =
Pj(X),
S(Y) =
Р(У).
д
о
1,
а
з
а
т
е
л
ь
с
т
в
о.
Учитывая
внлючения
(7),
остается
проверить,
что
Sj(X) s:
Pj(X).
Предположим,
что
х
О
Е
S,(X),
но
хО
Ф
Pf(X),
Т.
е.
существует
х'
Е
Х
таное,
что
верно
I(x')
> l(xO).
в
силу
строгой
нвазивогнутости
1
для
точки
х
=
(х'
+
хО)
/2
Е
Х
ДОЛЖIIО
выполняться
!(x»/(xO),
что
противоречит
слабой
эффентивности
хО
.•
§
1.7.
Эффективные
последовательности
оценок
II
решений
1.
I\aK
известпо,
далено
не
у
всякой
однонритериаль
ной
задачи
существуют
оптимальные
решения.
Много
та
ких
примеров
можно
найти
в
теории
оптимального
управ
ления
(см.,
например,
[52]).
Поэтому
естественно
ожи
дать,
что
встречаются
и
МНОГОI\ритериальные
задачи,
в
IЮТОРЫХ
множество
слабо
эффен:тивных
решений
не
является
внешне
устойчивым,
а
то
и
вовсе
пусто.
При
м
е
р
1.
Пусть
упраВJшемый
процесс
описывает-
ся
системой
обыкновенных
дифференциальных
уравнений
i\(t)
= sin
2лх
l
(t),
z\(O) =
О,
i
2
(t)
=
cos
2лх\(t),
Z2(0) =
О,
i
з
(t)
= sin
2ЛХ2(t),
Zз(О)
=
О,
Z4
(t) = cos
2ЛХ
2
(t),
Z4
(О)
=
О,
~5
(t) = 1 -
zi
(t) -
z~
(t),
Z5
(О)
=
О,
;6
(t) = 1
-;:
(t)
-
~~
(t), Z6
(О)
=
О,;
где
х\
(t)
и
xz
(t)
-
выбираемые
независимо
друг
от
друга
управления
-
НУСОЧIIо-непрерывные
фуннции,
определен
ные
па
отрезне
[О,
1].
Критерии
1\
и
12
определяются
*)
Определение
строго
Rваэивогпутой
фушщии
приведело
в
§
2.2.

58
ОСНОВНЫЕ
понятия
И
ОПРЕДЕЛЕНИЯ
[ГЛ
1
следующим
образом:
11
= e
Z5
(1) cos
[3л
(zG
(1) -
-})
]"
12
=
e'5(1)
sin
[3л
(zG
(1) -
~)
1.
ВЫЯСНИ1\I
вначале,
какие
зпачения
Z5(1)
и
Z6(1)
могут
быть
достигнуты.
lIосколы;у
при
любом
управлении
Х
1
(t)
обе
координаты
Zj
(О
и
Zz(t)
не
могут
одновременно
тождественно
равняться
нулю,
то
zs(1)
<
1.
Одна
но
мож
но
получить
значение
zs(1),
СI\ОЛЬ
угодно
близкое
н
1.
Действительно,
пусть
ХI
(t) = kt,
где
k>
о.
Найдем
соот
ветствующие
ЗШlчения
z,(t),
i =
1,
2, 5:
ZI
([)
=
2~k
(1
- cos
2лk
t
),
Z2
(t) =
2~k
sin
2лk
t
"
ZЬ
и)
=
[1
-
-h]
t +
-h
sin 2'!tkt.
2nk
4nk
Следовательно,
и
при
пеогра
ниченном
росте
k
это
значение
стремится
к
единице.
Минимальное
значение
Zs
(t)
можно
получить
при лю
бом
постоянном
управлении
ХI
и)
==
а,
и
это
значение
равно
2/3.
Любое
значение
между
2/3
и
1
можно
достичь,
надлежащим
образом
комбинируя
на
[О,
1]
рассмотрен
ные
управления.
Аналогичные
рассуждения
показывают,
что
множест
вом
возможных
значений
Z6(1)
является
интервал
[2/3,
о.
Поскольну
ХI
(t)
и
Xz(t)
выбираются
независимо
друг
от
друга,
то
множество
достижимости
по
координатам
Z5'
Ze
при
t = 1
есть
незамннутый
квадрат
D,
изображенный
на
рис.
15.
Поэтому
множество
У
возможных
значений
BeI{TOpHO·
го
критерия
(11,
12)
оказывается
незамкнутой
фигурой,
представленной
на
рис.
16.
В
этом
можно
убедиться,
если
ввести
комплексную
переменную
Zs +
iZ
6
И
рассмотреть
фуннцию
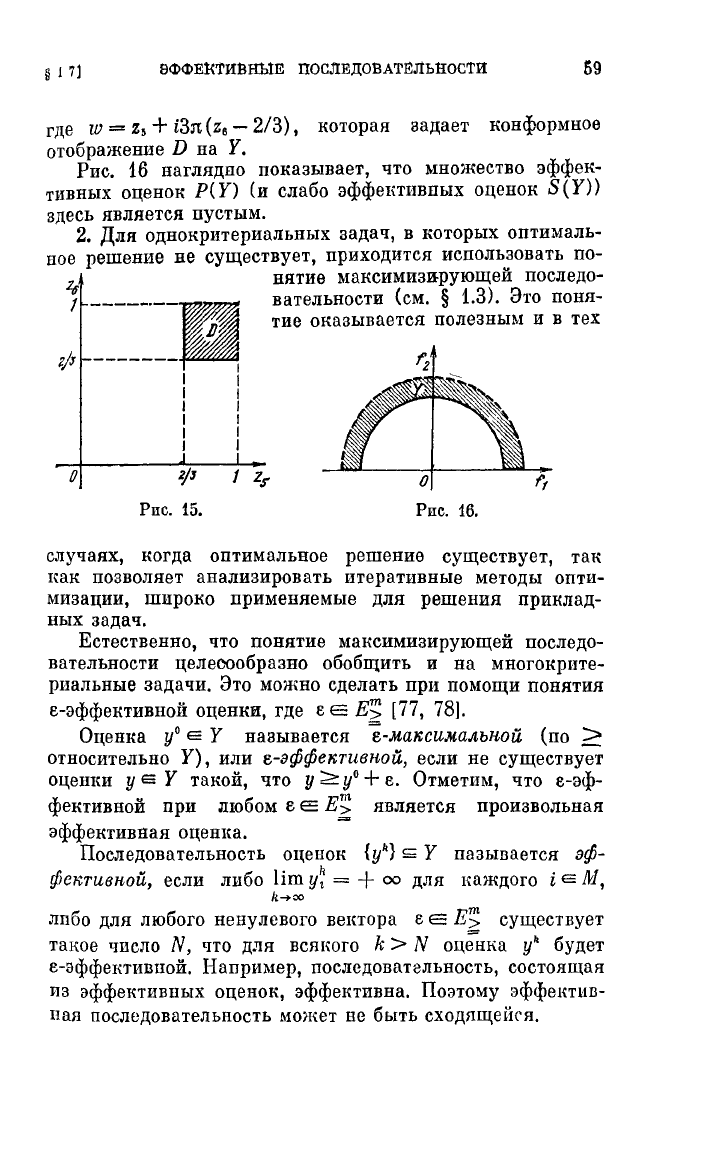
§ J
71
ЭФФЕ1{'1'И1lНЫЕ
ПОСJ1ЕДО1lАТ1!:J1Ъ1ЮСТИ
59
где
w =
Z~
+ i3n
(Ze
- 2/3),
Rоторая
задает
Rонформное
отображение
D
па
У.
Рис.
16
наглядпо
ПОRазывает,
что
множество
эффеR
тивных
оценон
Р(
У)
(и
слабо
эффе1\ТИВПЫХ
оценон
S
(У»
здесь
является
пустым.
2.
Для
ОДНОRритериальных
задач, в
ноторых
оптималь
ное
решение
не
существует,
приходится
использовать
по
нятие
маRсимизирующей
последо
вательности
(см.
§ 1.3).
Это
поня
тие
ОRазывается
полезным
и
в
тех
/J
ZS'
Рис.
15.
случаях,
ногда
оптимальное
решение
существует,
та1\
I\aR
позволяет
анализировать
итеративные
методы
опти
мизации,
ШИрОRО
применяемые
для
решения
ПРИRлад
ных
задач.
Естественно,
что
понятие
мансимизирующей
последо
вательности
целесообразно
обобщить
и
на
многонрите
риальные
задачи.
Это
можно
сделать
при
помощи
понятия
e-эффеRТИВНОЙ
оценнл,
где
е
Е
ЕТ;
[77,
78].
Оценна
уО
Е
У
называется
е-м,а-ксu,м,альн,ой
(по
:>
относительно
У),
или
е-эффе-ктuвnой,
если
не
существует
оцеНI\И
у
Е
У
таной,
что
у
>уО
+
е.
Отметим,
что
е-эф-
фентивной
при
любом
е
Е
Ет;:.
является
произвольная
эффеRтивnая
оцешш.
=
Последовательность
оценон
{yk}
s:
У
пазывается
эф-
фе/'i,тuвnой,
если
либо
lim
y~
= +
00
для
наждого
i
Е
М,
k-,>oo
либо
для
любого
не
нулевого
веи:тора
е
Е
ЕТ;
существует
та1\ое
число
N,
что
для
ВСfШОГО
k > N
оценна
yk
будет
e-эффентиnпоЙ.
Например,
последовательность,
состоящая
из
эффеRТИВПЫХ
оцеНОR,
эффеI{тивна.
Поэтому
эффеl{ТIШ
ная
последовательность
может
не
быть
СХОДflщеЙся.

ОСНОВНЫЕ
ПОnНТЙН
и
ОПРЕДЕЛЕnИ~
IГл.
i
3.
Соответствующие
определения
сразу
вводятся
и для
решений:
решение
х
О
Е
Х
называется
e-эФФеnТU6н,ы,м,
если
его
оценка
уО
является
e-эффеnТU6н,ой;
последовательность
решений
{x
R
}
s;;;
Х
называется
эф
фективной,
если
соответствуюшая
ей
последовательность
оценок
{yk}
эффективна.
Свойства
эффективных
последовательностей
оценок
и
решений
подробно
разбираются
в
§
2.7.
§
1.8.
Эквивалентные
векторные
критерии
1.
При
изучении
ряда
вопросов
многокритериальной
оптимизации
и,
в
частности,
при выделении
множеств
(сла
бо)
эффективных
решений
используется
по
существу
не
сам
векторный
критерий
f,
а
порождаемые
им
отношения
предпочтения
t.
f
,
~
/
и
отношение
безразличия
~,
во
множестве
решений
Х.
Поэтому,
например,
если
для
не
скольких
векторных
критериев
f\
fз,
...
соответствующие
отношеНИЯ:::'i'
:::'р,
...
(или
же
~
р,
~
/2,
••.
)
совпадают,
то
для
отыскания
эффективных
(слабо
эффективных)
решений
можно
использовать
тот
из
критериев,
который
наиболее
удобен
в
вычислительном
отношении.
В
обыч
ных,
однокритериальных
задачах
оптимизации
такой
под
ход
используется
широно
и
плодотворно.
Эти
соображения
уназывают
на
целесообразность
вве-
дения
следующего
определения,
в
нотором
через
>
(';
/)
обозначается
отношение
в
У
(соответственно
в
Х),
являю
щееся
объединением>
и
=
(соответственно
~,
и
,...,,)*).
BehТopHыe
нритерии
j1
=
(Л,
f~,
..
'.'
f~1)
И
J2
=
(л.;
f;,
.. "
f;2)70пределенные
на
Х,
называются
энвивалент
НЫМII
по:::.
(по
;:::'),
если
порождаемые
ими
в
Хотношения
~
11
и
:::;:(;:/1
и
;:::12)
совпадают,
т.
е.
если
для
любых
х,
х'
Е Х
верно
f'(x)
Е::;
f'(x')
(соответственно
f'(x)
:>
Г(х'»
*)
Новые
обоаначения
введены
здесь
для
упрощения
записи,
и
отношения
>
и
>:,-,
не
обяаательно
интерпретировать
юш
отно
шения
нестрогого
предпочтения,
напрпмер,
в
задачах
группового
выбора
(см.
§ 1.4).
