Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач
Подождите немного. Документ загружается.


§
1.4]
ЭФФЕКТИВНЫЕ
И
СЛАБО
ЭФФЕНТИВНЫЕ
РЕШЕНИЯ
31
H<lRO
оно
обязательно
будет
ВRлючать
отношение
>.
Раз
личными
могут
быть
также
отношения
не
строгого
пред
почтения
и
безразличия.
Вопросы
задания
всех
этих
от
ношений
достаточно
сложны
и
являются
предметом
ис
следования
теории
групповых
решений
[53,
56,
96,
109, 221].
3.
Итак,
для
многокритериальных
задач
максимизации
на
множестве
У
введены
отношение
не
строгого
предпоч-
тения
б:,
два
отношения
стро-
у*
гого
предпочтения
?
и
>
и
от
ношение
безразличия
=.
В
со
ответствии
с
общим
определе
нием
(§
1.2)
оценка
у*
Е
У
на
зывается
наилучшей
по
;;::::
I •
(в
У),
если
для
любой
оценки
-O+-------~!JI
У
Е
У
справедливо
У*;;::::
у.
Так
RaK
отношение
б:
является
Рис.
4.
(частичным)
порядком,
то
может
существовать
толыю
одна
такая
точка
у*
(рис.
4)*).
4.
Если
в
практической
многокритериальной
задаче
существует
наибольшая
по
б:
достижимая
оценка
у*,
то
именно
ее
и
следует считать
оптимальной.
R
сожалению,
таRОЙ
случай
реализуется
исключительно
редко:
как
пра
вило,
оценка
у* не
существует
**).
Это
связано
с
тем,
что
порядок
б:
не
является
полным.
Например,
если
Yi
>
У;
, '
но
Yj
<
Yj,
то
У
и
У'
по
~
не
сравнимы.
Поэтому,
в
зави-
симости
от
существа
задачи,
приходится
ИСПОЛЬЗ0вать
оценки,
ман:симальные
по
>
или
по
>
(см.
§ 1.2).
Оценка
у
О
Е
У
называется
максимальной
по
>
(по
»
относительно
У,
если
не
существует
оцеНRИ
У
Е
У
такой,
что
У
>
у
О
(у>
уО).
для
этих
оценок
обычно
используют
ся
специальные
названия.
Оценка,
максимальная
по
> ,
называется
эффеr>тuвnой
***),
а
также
оnтимальnой
по
Па
рето,
Парето-оnтuмальnой,
оптимумом
Парето.
Множество
*)
На
этом
и
последующих
рисунках
множество
У
не
изобра
Щено
(можно
считать,
что
f -
все
пространство
Е2).
**)
Условия
существования
наибольшей
по
~
точки
см.
в
статье
[1221
и
указанной
там
литературе.
***)
Термины
«эффективный»
и
«f-эффеКТIIвныii»
(см.
ниже)
введены
Т,
Купмансом
(184J.
32
ОСНОВНЫЕ
понятия
и
ОПРЕДЕЛЕНИЯ
[ГЛ.
i
всех
таких
оцено!,
из
У,
обозначаемое
далее
через
Р(
У),
называется
эффе-"тuвuым,
или
мuожеством
Парето.
Оценка,
максимальная
по
>,
называется
СJtабо
эффеl~
тuвuой,
а
также
сJtабо
onTUMaJtbuou
по
Парето,
СJtабым
оптимумом
Парето,
оnти,мдJtьuоu
по
CJteuTepy
*).
Мно
жество
всех
таких
оценок
из
У
будем
обозначать
через
S(Y)
и
называть
сJtабо
эффе-"тuвuым.
Поскольну
у
>
у'
влечет
у >у',
то
всякая
эффективная
относительно
У
векторная
оценка
и
слабо
эффективна,
так
что
р(у)
s=
S(Y).
Действительно,
если
уО
не
является
слабо
эффективной,
то
для
неноторой
у
Е
У
будет
выпол
няться
у>
уО,
а
поэтому
и
у
2:
уО,
так что
уО
не
может
быть
эффективной.
При
т
==
2
р(у)
является,
образно
говоря,
северо
восточной
границей
множества
У
(без
тех
ее
частей,
ко
торые
параллельны
одной
из
координатных
осей
или
ле
жат
в
достаточно
крутых и
глубоких
провалах),
а
S(Y)
может
дополнительно
включать
в
себя
вертикальные
и
го
ризонтальные
участки
границы,
прилегающие
н
Р(
У},.
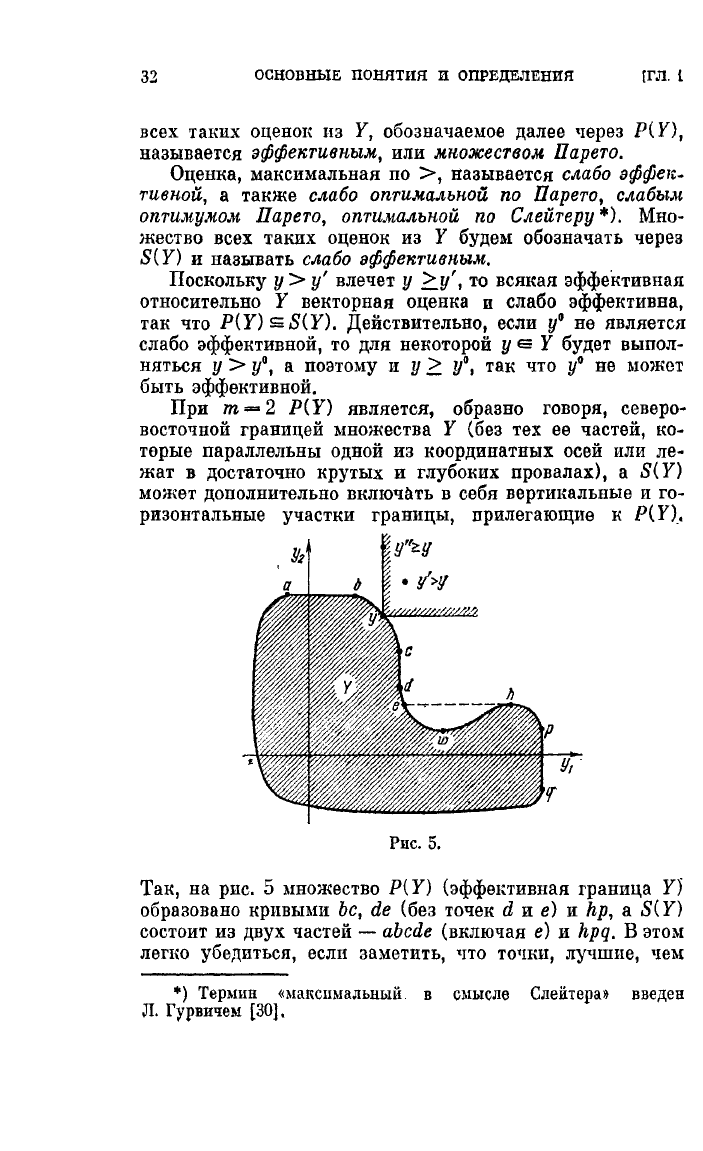
Рис.
5.
Так,
на
рис.
5
множество
Р( У)
(эффеl<тивная
граница
У)
образовано
кривыми
Ьс,
de
(без
точен
d
и
е)
и
hp,
а
S(Y)
состоит
из
двух
частей
-
abcde
(включая
е)
и
hpq.
В
этом
леГ1\О
убедиться,
если
заметить,
что
точни,
лучшие,
чем
.)
Термин
<ЩaI\СlIмальпыЙ.
в
смысле
Слейтера»
введен
Л.
Гурвичем
[30].

§
1.1.]
ЭФФЕRТИВНЫЕ
и
СЛАБО
ЭФФЕRТИВНЬШ
РЕШЕНИЯ
33
у,
в
смысле
>,
заполняют
прямой
угол,
стороны
которого
параллельны
осям
координат,
а
веРШИIIОЙ
служит
точка
у
(сама
у
исключается);
а
точки,
лучшие,
чем
у,
в
смысле
>,
состаВШIЮТ
внутренность
этого
же
угла.
5.
Отношения
:>,
>
и
>,
определенные
на
множестве
оценон,
порождают
аналогичные
по
смыслу
отношения
::'j'
!:.!
и
'r
J
во
множестве
решений.
Например,
Х
::'jX'-
::!
(Х)
:>
!
(х').
Отношение
;;:'/
является
(частичным)
ква
зинорядком,
а
::'/
И
'r!
-
строгими
(частичными)
по
рядками.
Напомним,
что
отношенпе
безразличия
"'"
/,
по
рожденное
отношением
paBellcTBa
=,
является
эквива
лентностью
(см.
§ 1.3).
Решению,
напбольшему
по
;;/'
соответствует
наи
большая
по
;;;:::
оценка
из
У.
Следовательно,
наибольшее
по;;/
решение
обращает
в
ман:симум
на
Х
каждыIй
из
н:ритериев
!!,
!~,
... ,
jm.
Такие
решения,
как
уже
отмеча
лось,
безусловно
могут
считаться
оптимальными,
однако
практически
они
почти
никогда
не
существуют.
Решению,
максимальному
по
::./
(по
'r
/),
соответ
ствует
JlIаксимальная
по
~
(по
»
оценка
в
У.
Обычно
для
этих
решений
используются
наименовапия,
аналогич
ные
назваНИЯJII
соответствующих
оценок.
В
дальнейшем
будут
использоваться
термины
«эффективное»
и
«слабо
эффективное»,
а
таЮI\е
«оптималыюе
по
Парето»
и
«слабо
оптимальное
по
Парето
решению)
(заметим,
что
иногда
такие
решения
называют
j-эффеI{ТИВНЬГМИ
и
слабо
j-эф
феI{ТИВНЫМИ
соответственно).
Итак,
решение
ХО
Е
Х
эффективно,
если
не
существу
r,T
решения
Х
Е
Х
такого,
что
Х
:::/хО,
т.
е.
для
которого
!(х)
> j(XO).
Решение
ХО
Е
Х
слабо
эффективно,
если не
существует
решения
х
Е
Х
такого,
что
Х
'>-jХО,
т.
е.
j(x)
>
>
!(хО).
:Множество
эффективных
решений
будет
обозна
чаться
через
Pj(X),
а
слабо
эффективных
-
через
S/X).
Разумеется,
Pj(X)
s
Sj(X).
Отметим,
что задача
постро
ения
множества
Pj(X)
названа
в
[41,
187]
задачей
вен
торной
максимизации.
При
м
е
ч
а
н и
е
1.
В
соответствии
с
общими
сообра
жениями,
изложенными
в
примечании
1
к
§ 1.2,
поня
тие
эффективного
решения
теряет
свое
значение,
когда
требуется
выбрать
неСI\ОЛЫ,о
лучших
решений.
3
в.
В.
Подиновений.
В.
д.
Ноrин

ОСНОВНЫЕ
понятия
И
ОПРЕДЕЛЕНИЯ
[ГЛ.
t
6,
Согласно
определению
внешней
устойчивости,
дан
ному
в
§ 1.2,
множество
эффеКТИВIIЫХ
оцеНОI,
р(
у)
(сла
бо
эффективныIx
оценок
S(
У»
называется
внешне
устой
чивым,
если
для
любого
у
Е
у\р(
у)
(соответственно
для
у
Е
Y\S(
У»
найдется
ТaI{ая
оценка
уО
Е
р(
у)
(соответ
ственно
уО
Е
S(
УН,
что
уО
2:
У
(соответственно
уО>
у),
ECTecTlIeHHo,
можно
говорить
и
о
внешне
устойчивом
мно
жестве
эффективных
(слабо
эффективных)
решений
как
о
мпожестве
решений,
которому
соответствует
внешне
ус
тойчивое
мпожество
эффективных
(слабо
эффективных)
оценок,
В
дальнейшем
удобнее
использовать
несколько
иное
определение
внешней
устойчивости
множества
эффектив
ных
оценок:
множество
р(
у)
вllешне
устойчиво,
если
дЛJt
любого
у
Е
У
найдется
уО
Е
р(
у)
тапой,
что
уО::?:
у.
Лег
ко
видеть,
что
данное
определение
эквивалентно
в:ыше
приведенному
*),
Действительно,
пусть
р(
у)
внешне
устойчиво
в
смыс
ле
первого
из
рассмотренных
определений.
Возьмем
про
извольную
оценку
у
Е
У.
Если
у
Е
р(у),
то
верно
уО::?:
у
для
уО
=
у.
Если
же
у
Ф
р(
У),
то
существует
такая
оцен
ка
уО
Е
р(
N,
что
уО::>
у,
так
что
верно
и
уО
G;
у,
Пусть
теперь,
наоборот,
р(
у)
внешне
устойчиво
в
смысле
вто
рого
определения,
Выберем
произвольную
оценку
у
Е
Е
у\р(
N,
ДJIЯ
нее
найдется
оценка
уО
Е
р(
у)
такая,
что
уО
G;
у.
Но
так
как
у
не эффеI\тивна,
а уО
эффективна,
то
уО::>у
.•
Согласно
сделанному
в
§ 1.2
замечанию
о
существо
вании
ядра
квазипорядна
на
конечном
множестве,
можно
утверждать,
что
если
множество
У
состоит из
конечного
числа
оценок,
то
множества
эффеитивных
и
слабо
эффек
тивных
оценои
и
реше
пий
являются
внешне
устойчивыми.
Если
же
У
бескопечно,
то
указанные множества
могут
не
быть
впешне
устойчивыми.
Однако
при
обычпых
для
оп
тимизационных
задач
предположениях
(Х
-
иомпакт,
а
все
fi
полунепрерыnны
сверху)
эти
множества
ОI\азыnа
ются
внешне
устойчивыми
(см.
§ 3.2).
При
м
е
р
1.
Пусть
У
-
единичный
Iшадрат,
из
IЮ
торого
<<Вьшолота»
правая
верхняя
вершина
(рис.
6).
Для
*)
Следовательно,
внешняя
устойчивость
множества
Р
(У)
03-
начает,
что
частично
упорядоченное
(отношением
::?:)
множеСТВQ
У
копфинально
с
Р(У)
(см.
[50],
т.
1,
с.
33).

§
1,4]
ЭФФЕНТИВНЫЕ
И
СЛАБО
ЭФФЕНТИВНЫЕ
РЕШЕНИЯ
35
этого
У
множество
р(
У),
очеRИДНО,
пусто,
а
S(
У)
образу
ется
верхней
и
правой
сторонами
квадрата
(боз
точки
(1,
1).
МножеСТRО
S(Y)
внешне
устойчиво:
каждой
точ
ке
У
Е
У,
у
которой
YI,
Уз
<
1,
можно
поставить
в
соот-
О
(У
1
+ 1
1)
о
ветствие,
например,
точку
У
= 2 '
,причем
у
>у.
В
связи
с
изложенным
представляет
интерес
вопрос
о
том,
Iюгда
внешняя
устойчивость
множества
р(
У)
равносильна
аналогич
ному
свойству
множества
S(Y)?
Ответ
па
этот
вопрос
содержится
в
следую
щем
утверждении.
т
е
о р
е
м
а
1.
Если
М1l0жество
Р( У)
вllеШllе
устойчиво,
то
вllеШllе
ус
тоЙчивЫ}.t
является
и
S(Y).
В
том
слу-
~
О
уО
: /
1 /
1 /
1/
.у
чае,
когда
М1l0жество
R(y)
=
{у'
Е
УI
Рис.
6.
'у'
~
У}
8амКllУТО
и
ограnиЧe1l0
при
I !/,
J1Jобом
У
Е
S(
У),
и8
вllеШllей
устойчивости
S(Y)
следует
вllеШllЯЯ
устоiJ,чивость
р(у).
Д
о
и
а
з
а т
е
л
ь
с т
в
о.
Пусть
р(
У)
внешне
устойчиво.
Возьмем
ПРОИЗRОЛЬНУЮ
оцепиу
у
Е
Y\S(Y).
ДЛЯ
нее
су
ществует
у'
Е
S(Y)
такая,
что
у'
>
у.
Для
у',
в
свою
оче
редь,
существует
эффеитивпая
оцениа
у"
такая,
что
у"
~
у'.
Следовательно,
у"
>
у.
А
таи
иаи
р(у)
s=
S(Л,
то
у"
Е S(Y).
ДЛЯ
доиазательства
второй
части
теоремы
таиже
возь
мом
произвольную
оцепиу
у*
Е
У.
Если
у*
Е
р(у),
то
.110
~
у*
при
уО
=
у*.
Если
у*
Ф
S(
У),
то
для
неиоторой
оцешш
уО
Е
S(
У)
В,ерно
уО
>-
.11*.
Поэтому
остается
рассмотреть
случай,
когда
у*
Ф
р(у),
но
у*
Е
S(Y).
Благодаря
иомпаI>тности
множества
R{y*)
фуниция
т
,~Y;
достигает
на
нем
маИСИ~lума
в
неиоторой
точие
'=1
уО.
Предположив
противное,
легио
убеднться
в
том,
что
уО
е
р(
У)
(этот
вынод
прямо
следует
из
лемм
2.4-2.6,
таи
каи
множество
R(y*)
заllНШУТО
сверху
по
>-
относи
тельно
У).
Кроме
того,
в
силу
определепия
R(y)
справед-
ЛПЩJ
уО
~
у*.
18
'
7.
Пусть
R -
ПРОИЗDОЛЫIЫЙ
КRaЗИПОРЯДОR
на
множе
Стве
Х.
Веиторный
I\рптерий
j,
определенный
на
Х,
пред
ставляет
Rвазипорядои
R,
если
отношение
;:
t
совпадает
3*

ОСНОВНЫЕ
понятия
и
ОIIPЕДЕЛЕНИЯ
[ГЛ.
i
с
R.
При
наних
условиях
существует
векторный
крите
рий,
представляющий
произвольный
квазипорядок?
Ка
кова
минимальная
размерность
таного
нритерия?
Как
его
построить?
Исследование
этих
вопросов
имеет
не
только
теоретичеСlюе,
но и
прюпическое
значение.
Например,
указание
представляющего
критерия
может
оказаться
экономным
способом
задания
квазипорядка.
Однано
пере
численные
вопросы
не
имеют
прямого
отношения
к теме
книги,
и
поэтому
мы
их
разбирать
не
будем.
Заинтере
сованный
читатель
может
обратиться к
соответствующей
литературе
[60,74,
123, 170, 190].
8.
Один
из
способов
задания
отношений
предпочтения
в
многокритериальных
задачах
состоит
в
следующем:
в
пространстве
Ет
выделяется
неноторый
конус
Q
(".оnус
дОJ<шnuроваnuя)
,
и
полагается,
что
yR{Jy',
когда
у-у'
eQ.
Понятно,
что
при
Q =
E~
получается
отношение
~,
а
при
Q =
Е;:
-
отношение
>.
Следовательно,
много
критернальная
задача
максимизации
является
частным
случаем
задачи
оптимизации
по
копусу
[30, 246].
Рассмотрим
случай,
когда
конус
Q
является
полиэд
..
ральным
(многогранным):
Q =
{у
е
EmlBy;;;:":
0(1),
где
В
-
это
числовая
матрица
размерности
l
Х
m.
Для
такого
конуса
включение
у
-
у'
е
Q
равносильно
тому,
что
В(у
-
у')
;;:::
0(1),
т. е.
Ву;;;:":
Ву'.
Следовательно,
исходная
задача
с
венторным
критерием
f,
в
которой
предпочтения
задаются
при
помощи
полиэдрального
конуса,
после
введе-
ния
нового
векторного
критерия
fB=(tf,
f:,
..
','
ff)=
В!
оказывается
«обычной»
многокритериальной
вадачей
мак
симизации
[150, 247].
9.
Определение
(слабо)
эффективного
решения
являет
ся
«статическим»
в
том
смысле,
что
основывается
на
по
парном
сравнении
решений
и
не
связывается
с
вопросом
о
том,
возможно
ли
(<плавно»
перейти
от
одного
решения
к
другому,
более
предпочти!ельному,
инфинитезималыIo
«<с
положительной
скоростью»)
увеличивая
каждый
кри
терий.
А
возможность
осуществления
такого
перехода
в
неноторых
моделях
представляет
большой
интерес.
При
мером
является
модель
чистого
обмена,
в
ноторой
наЖ
дый
потребитель
участвует
в
обмене,
стремясь
составить
себе
набор
товаров
наибольшей
полезности,
т. е.
фор
малыo
-
мансим:изировать
свою
функцию
ценности.
Та-

§
1.4}
ВФф1!:}{'l'ИВНЫЕ:n
СЛАВО
ЭфФЕ1{ТИВН'Ь1Е
РЕmЕниfl:
37
кого
рода
модели
рассматривали
еще
в
XIX
в.
Ф.
Эдж
порт
Il
В.
Парето.
Эффективным
в
модели
обмена
являет
ся
состояние
(распределение
товаров
между
потребителя
ми),
ноторое
не
может
быть
улучшено
путем
перерас
пределения
товаров
ни
для
одного
из
участников
без
«ущемления
интересов»
некоторых
других
участников.
Следовательно,
оптимальность
по
Парето
отражает
идею
экономического
равновесия:
если
состояние
не
является
эффентивным,
то
будет
происходить
торговля,
которая
приведет
1\
эффективному
состоянию.
Если
процесс
обмена
рассматривать
как
последова
тельность
меЛЮIХ
сделок,
выгодных
всем
участникам,
то
формализованно
его
можно
описать
гладной
кривой,
при
движении
вдоль
которой
все
критерии
инфинитезимально
увеличиваются.
Тогда
можно
выделить
состояния,
из
ко
торых
не
выходит
ни
одной
гладкой
кривой
такого
типа.
Такие
состояния
были
названы
С.
Смейлом
критическими
точнами
Парето.
Ясно,
что
множество
таких
точек
(кри
тическое
множество
Парето)
включает
все
множество
сла
бо
вффентивных
точек,
но
в
общем
случае
шире
послед
него
(из-за -'<локального
характерю)
определения
крити
чесной
ТОЧЮI
Парето). Тан,
на
рис.
5
в
критическое
мно
жество
Парето,
помимо
всех
слабо
эффективных,
будут
входить
решения,
оценки
которых
лежат
на
участке
гра
ницы
еш.
Определение
критичесной
точни
Парето
является
обоб
щением
стационарной
(нритичесной)
точни
гладной
фуш\
ции
(т.
е.
точки,
в
которой
ее
градиент
обращается
в нуль).
Подробное
рассмотрение
описанного
«динамичесного»
подхода
к
определению
оптимальности
по
Парето
выходит
за
рамки
данной
книги;
заинтересованному
читателю
сле
дует
обратиться
1\
работам
С.
Смейла
[95, 223].
10.
:Множества
эффентивпых
и
слабо
эффективных
оценок
были
выделены
из
У
на
основе
некоторых
прос
тых
характерных
свойств
отношений
предпочтения.
Однано
.
эти
множества
целесообразно
рассматривать
и
в
более
общей
ситуации,
когда
предполагается
лишь,
что
нредпочтения
описываются
фуннцией
выбора
С,
опреде
ленной
на
достаточно
«богатом»
наборе
W
подмножеств
множества
У
(разумеется,
у
Е
W).
в
рассматрпваемом
случае
многокритериальная
задача
мансимизации
онределяется
следующим
условием:
если

ЬСНОВНЫЕ
ttонятйя
И
ОПРЕДЕnЕНИЙ
(r'Л.l
, " Z Z W " , " ,
оценки
У,
У
Е
,
Е
,таковы,
что
Yj
>У;
и
У!
=
У!
для
всех
т
- 1
остальных
i
Е
М,
ТО
У'
Ф
C(Z).
Ансиома
Парето
в
сильном
(слабом)
варианте
форму
лируется
следующим
образом:
если
для
оценни
у'
Е
Z,
Z
Е
W,
во
множестве
Z
найдется
оценка
у"
такая,
что
У;
:>
У;
при
всех
i
Е
М,
причем
хотя
бы
одно
неравен
ство
строгое
(у7
>
У;
прп
всех
i
Е
М),
то
у'
Ф
C(Z).
Эта
аксиома,
из
которой
вытекает,
что
с(у)!:
р(у)
(соответственно
С( У)
!:
S(
У)),
часто
используется
при
описании
предпочтений
функциями
выбора
[53, 96],
§ 1.5.
Теоретичесное
и
практичеСIюе
значения
понятия
эффективного
решения"')
1.
Понятие
эффентивного
решения
является
прямым
обобщением
понятия
точки
мансимума
числовой
функции
на
случай
неснольких
фуннциЙ.
Как
правило,
в
приклад
ных
многокритериальных
задачах
множество
таких
реше
ний
оназывается
непустым
и,
более
того,
внешне
устой
чивым
(см,
§ 1.4),
и
поэтому
оптимальные
решения
долж
ны
выбираться
именпо
среди
эффективных.
Однако
если
в
однокритериальной
задаче
в
качестве
оптимального
можно
брать
любое
решение,
мансимизирующее
критерий
(так
как
все
они
;н\Вивалентпы),
то
в
многокритериальной
задаче
обычно
множество
эффективных
решений
оказы
вается
весьма
богатым
неэквивалентными-(и
содержатель
но
существенно
разными)
решениями,
и для
осмысленного
выбора
оптимального
решеJ3.ИЯ
необходимо
привлечь
бо
лее
полную
информацию
о
предпочтениях.
И
тем
не ме
нее
ПОl'Iятие
эффективного
решения
по
целому
ряду
при
ЧIIН
играет
важнейшую
роль
в
теории
многокритериаль
ной
оптимизации
и
практике
ее
использования.
2.
Хотя
эффективное
решение
обычно
далено
не
един
ственно,
но
bce-таЮI
множество
эффентивных
решений
значительно
уже,
чем
исходное
множество
всех
решений.
Так,
на
рис.
5
множество
эффен:тивных
оценон
является
лишь
частью
границы
множества
всех
достижимых
оце-
*)
в
дальнейшем
ради
I\раТI\ОСТИ
термин
«эффеl\тивное
реше
ние»
будет
таЮRе
испольаоватьсл
и
внеформальном
I\онтю{сте
I\аl\
обобщающий
длл
эффеЮIIВНЫХ
и
слабо
эффективных
(а
впоследст
вии
и
длл
собствешю
и
подлинно
эффективных)
решений.

§ 1,5]
ЗНАЧЕНИЕ
понятия
ЭФФЕНТИВНОГО
РЕШЕНИЯ
39
НОК.
Поэтому
FIостроение
множества
эффективных
реше
ний
(или
их
оценок)
является
одним
из
первых
этапов
большого
числа
процедур
(особенно
интерактивных,
т. е.
человеко-машцнных)
и
методов
многокритериальной
опти
мизации
(см.,
например,
[47,
73,
88]).
А
некоторые
ин
терактивные
методы
предусматривают
последовательное
перемещение
от
одпого
эффективного,
решения
к
другому,
более
предпочтительному.
3.
В
случаях
наличия
лишь
двух
или
трех
критериев
множество
эффективных
оцеНОI{
можно
изобразить
графи
чески.
Поэтому при
анализе
двух-,
а
иногда
и
трехкри
териальных
задач
нередко
удобнее
всего
выбирать
опти
мальное
решение
непосредственно
на
основе
рассмотрения
графика
эффективных
оценок
(см.,
в
частности,
[33, 133,
135]).
Указанный
подход
лежит,
например,
в
основе
мето
да
«стоимость
-
эффентивность»
[8].
Один
из
вариантов
этото
метода,
широко
применяемо
го
для
решения
задач
выбора
лучшего
И8
нескольких
IЮНКУРИРУЮЩИХ
образцов системы,
в
общих
чертах
состо
ит
в
следующем.
а)
'Каждый
образец х
оценивается
по
двум
критериям:
стоимости
создания
(производства)
С
и
эффективности
выполнения
поставлен
ных
перед
системой
за
дач
э.
Значения
этих
нритериев
рассчитыва
ются
по
специально
раз
рабатываемьш
методи
I\aM.
б)
Строится
график
оценок,
соответствую-
1
•
о
/J
J
•
4
•
'о
J'
щих
всем
рассматривае-
,
О
С
мым
образцам
систеиы,
а
из
него
выделяются
Рис.
7.
те
образцы,
из
которых
и
должен
быть
выбран
один
-
оптимальный
образец.
Пример
такого
графИI{а
приведен
на
рис.
7.
Поскольку
Rритерий
С
желательно
мипимизировать,
а
нритерий
Э
-
маRСIIмизировать,
то,
например,
образец
4
предпочти
тельнее
образца
2
(последний
имеет
меньшую
эффектив
НОсть
и
в
1'0
же
время
большую
стоимость).
Танпм
образом,
из
шести
представленных
образцов
лишь
три

40
ОСНОВНЫЕ
понятия
и
ОПРЕДЕЛЕНИЯ
[ГЛ.
1
(первый,
третий
и
четвертый)
могут
претендовать
на
роль
лучшего.
В
разбираемом
методе
эти
образцы
называют
недоминируемыми
(общий
термин
«эффективный»
неудо
бен
из-за
аналогичного
названия
критерия
Э).
в)
ОIюнчательный
выбор
оптимального
образца
произ
водится
эвристически
(на
основании
опыта,
интуиции,
не
формализуемых
соображений)
лицом,
принимающим
ре
шение,
в
результате
анализа
построенного
графика,
кото
рый
наглядно
показывает,
накой ценой
(увеличением
стоимости)
достигается
приращение
эффективности
при
переходе
от
одного
недоминируемого
образца
к
другому.
Обобщением
рассмотренного
метода
является
метод
«стоимость
-
эффективность
-
времю),
в
котором
наряду
с
двумя
перечисленными
ранее
вводится
еще
критерий
т
-
время,
необходимое
для
организации
выпуска
того
или
иного
образца
системы.
В
этом
случае
графин
вен
торных
оценок
оказывается
пространственным
и
изобра
жается
в
наиболее
наглядной
плоской
проекции
или
же
представляется
несколькими
плоскими
сечениями.
Об
щий
подход
н
выбору
оптимального
образца
остается
прежним.
4.
Сужение
множества
выбора
до
множества
эффек
тивных
решений
(или
нен:оторого
его
подмножества)
важ
но
не
только
само
по
себе,
но
еще
и
потому,
что
на
бо
лее
узком
подмножестве
могут
выполняться
различного
рода
упрощающие
дальнейший
анализ
допущеНIIЯ
о
пред
почтениях
(например,
о
виде
функции
ценности),
ноторые
заведомо
несправедливы
для
множества
всех
решений.
Кроме
того,
эффективные
решения
могут
обладать
инте
ресными
и
практически
важными
свойствами,
не
прису
щими
остальным решениям.
Это
обстоятельство
хорошо
известно
и
давно
используется
в
математической
экономи
не
и
теории
игр.
Много
примеров
такого
рода
можно
най
ти,
например,
в
работах
[28, 33, 41, 51, 63].
Здесь
же
мы
ограничимся
рассмотрением
одного
сравнительно
просто
го,
но
содержательного
примера,
связанного
с
линейной
моделью
производства.
Пусть
имеется
n
отраслей,
занятых
производством
n
предметов
потребления
(продуктов).
Каждая
отрасль
мо
жет
производить
тольно
один
продунт,
но
при
помощи
нескольких
производственных
(технологических)
про
цессов.
ОБQзначим
через
А
!
множество
производствепных
