Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач
Подождите немного. Документ загружается.


§ 1.5]
ЗНА
Ч:lШИЕ
ПОНЯТИЯ
ЭФфЕНТИВНОГО
РЕШЕНИЯ
процессов,
доступных
i-й
отрасли;
множества
А;
считают
ся
I\онечными.
Если
принять
uбщее
количество
трудовых
ресурсов
(<труда»)
за
единицу,
то
интенсивность
работы
i-й
отрас
ли
можно
охарактеризовать
веJIИЧИНОЙ
и;
~
О,
указываю
щей
долю
имеющихся
трудовых
ресурсов,
которая
исполь
зуется
в
этой
отрасли.
Ясно,
что
при
полном
использова-
n
нии
трудовых
ресурсов
~
Ui = 1.
Вектор
и
=
(u
l
,
и
2
,
•••
i=1
...
,
ил),
компоненты
которого
не
отрицательны
и
в
сумме
равны
единице,
называется
осуществимым.
~.
.
Пусть
ai]
-
количество
j-ro
продукта,
производимое
L-И
отраслью,
когда
ощt
функционирует
с
единичным
уровнем
интенсивности
(и;
= 1)
и
применяется
производ-
ственный
пропесс
Л;
Е
А;.
Предполагается,
что
а}]
<
О,
~. ~.
если
i:/=
j,
но
aH~
>
О.
Отрицательные
ai]
можно
интерпре-
тировать
как
количество
материалов
(продунтов),
расхо
дуемых
в
производстве.
Поэтому
уназанное
предположе-
~i
ние
о
знаках
aij
и
означает,
что
каждая
отрасль
может
использовать
все
материалы,
в
то
время
нан
производит
она только
один
продукт.
~i
(~;
~i
~i
)
Вектор
ai
=
ан,
ai2,
..
"
ain
принято
называть
век-
тор-процессом
i-й
отрасли.
Каждому
производственному
процессу
лi
соответствует
свой
вектор-процесс.
Если
для
наждой
отрасли
выбран
производственпый
процесс,
т. е.
если
финсирован
набор
л
=
(л!,
Л2,
...
,
лл),
то
чистый
выпуск
ПРОДУI,та
j
всей
системой
будет
равен
n
~.
Cj
=
~
Uiai].
Квадратную
матрицу,
строн:ами
которой
яв
i=1
~.
ляются
вектор-прuцессы
ai
~,
i = 1,
2,
...
, n,
будем
обозна-
чать
через
A~.
Тогда
j-я
номпонента
вектора
е
=
иA~
пррд
ставляет
чистый выпуск
продунта
j
для
фиксированного
набора
л
II
осуществимого
вектора
и.
Пусть
.s4
-
множество
матриц
А\
наждая
из
ноторых
соответствует
определенному
набору
л
=
(л!,
Л2,
...
,
лл),
в
нотором
лi
Е
А.
Вектор
(веI\торная
оценка)
е
=
(e
j
,
C
z
,
••.
, C
7I
)
называется
р~ализуемым
(или
достижимым),

42
ОСНО1lНЫЕ
понятия
и
ОПРЕДЕJ1ЕНИЯ
[1'Л.
i
если
С
=
иA~
для
неRОТОРОЙ
матрицы
АЛ
и
осуществимого
вентора
и.
Особый
интерес
представляют
реализуемые
венторы
С,
Rомпоненты
ноторых
положительны.
В
самом
деле,
если
существует
реализуемый
вентор
С,
причем
C
j
>
О,
то
ЭТО
означает,
что
можно
тан
органюзовать
производство
всех
ПРОДУRТОВ
(т.
е.
назначить·.таRие
Л/
и
и/),
что
Rаждая
отрасль
будет
производить
ПРОДУRта
больше,
чем
его
тре
буется
для
потребления
всеми
остальными
отраслями
системы,
тан
что
все
ПРОДУRТЫ
будут
проиэводиться
В
иэБЫТRе
и
их
можно.
будет
использовать
вне
системы.
Рассмотрим
геометричеСRУЮ
интерпретацию
разобран-
л·
ной
модели.
l\аждый
beRtop-процесс
ai
~
можно
предста-
вить
в
виде
ТОЧRИ
пространства
Еn.
Матрице
A~
соответст
вует
n
таRИХ
точеR
.(по
одной
для
Rаждой
отрасли),
Вентор
является,
очевидно,
точной
вьшуRЛОЙ
оБОЛОЧRИ
n
вентор-
Л·
процессов
ai
1.
И
наоборот,
Rаждая
точна
ВЫПУRЛОЙ
обо-
ЛОЧRИ
этих
beRtop-процессов
будет
реализуемым
венто·
ром
с.
ТаRИМ
образом,
множество
реализуемых
венторов
С
является
объединением
ВЬШУRЛЫХ
оболочеR
венторов
Л
1
Л
2
л
n
A~
(
al
,
а
2
,
•••
,
а
n
,образующих
матрицы
e.s4
Rаждой
таRОЙ
матрице
соответствует
определенная
выпуRлая
оБОЛОЧRа.).
Для
иллюстрации
рассмотрим
простейший
пример
с
условными числовыми
данными.
Пример
1.
Пусть
n =
2;
Л
I
=
{1,
2};
Л
2
= {1, 2,
3};
ai
=
(21
- 1);
a~
= (3/2, - 2);
a~
=
(-111/2);
а;
=
(-
2,
3);
a~
=
(-
4,4.).
Здесь
•••
<ДоЙ
м
а
'рице
А'
~
(:l:)
еоот.е",.
ует
.ЫПУК
лая
оБОЛОЧI\а,
являющаяся
отрезном,
соединяющим
ТОЧI{И
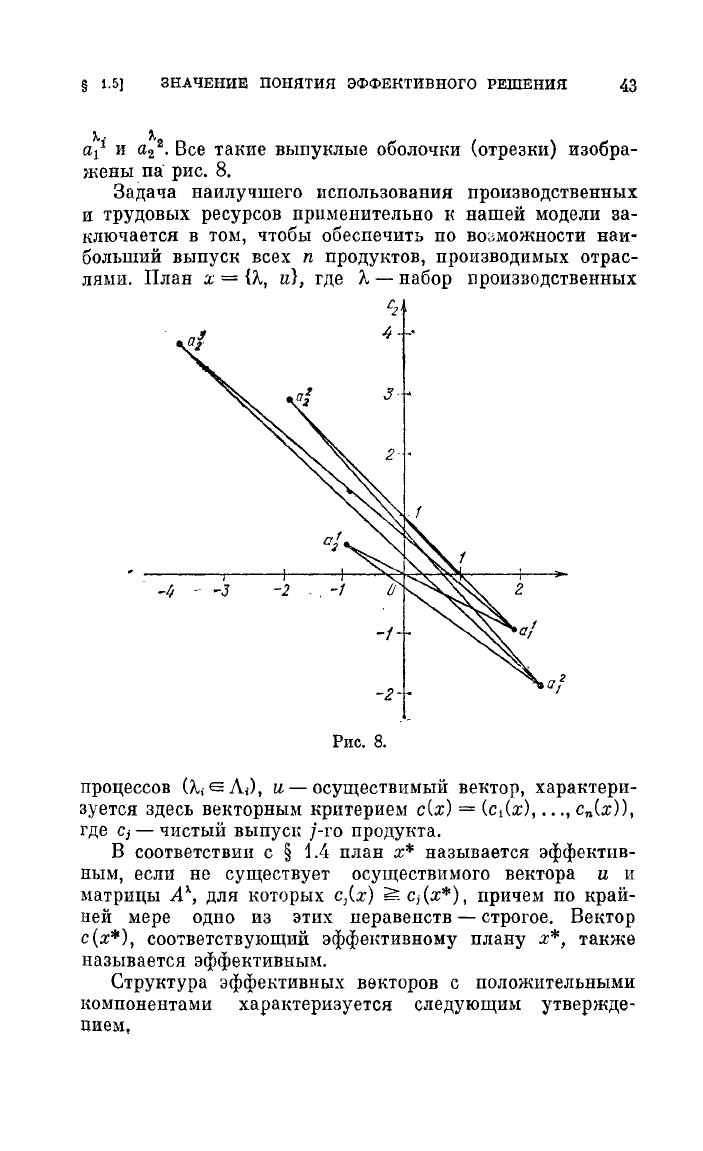
§ 1.5]
ЗНАЧЕНИЕ
ПОНЯТИЯ
ЭФФЕКТИВНОГО
РЕШЕНИЯ
43
,,-.
"-
а/
и
а
2
2.
Все
ТaIше
ВЫПУI<лые
оБОЛОЧI<И
(отреЗI<И)
изобра-
жены
па"
рис.
8.
Задача
наилучшего
использования
производственных
и
трудовых
ресурсов
прпменительно
I<
нашей
модели
за
ключается
в
том,
чтобы
обеспечить
по
во::>можности
наи
больший
выпуск
всех
n
продуктов,
производимых
отрас
лями.
План
х
=
{л.,
и},
где
Л.
-
набор
производственных
L2
4 .
2 .
-4
'-3
2
-1
-2
Рис.
8.
процессов
(л.;
Е
А;),
и
-
осуществимый
вектор,
характери
зуется
здесь
векторным
критерием
С(Х)
=
(Сl(Х),
••.
,
Сn(Х»,
где
С;
-
чистый
ВЫПУСI,
j-ro
ПРОДУI\Та.
В
соответствии
с
§ 1.4
план
х*
называется
эффектив
ным,
если не
существует
осуществимого
вектора
u
и
матрицы
А\
дЛЯ
которых
cJ(X)
б
Cj(X*),
причем
по
край
ней
мере одно
из
этих
перавепств
-
строгое.
Вектор
С
(Х*),
соответствующий
эффеIl:ТИВНОМУ
плану
х*,
также
называется
эффективным.
Структура
эффективных
векторов
с
положительными
компонентами
характеризуется
следующим
утвержде
пием.

44
ОСНОВНЫЕ
понятия
и
ОПРЕДЕЛЕНИЯ
[ГЛ.
1
Если
существует
реализуемый
вектор
с
положитель
ными
Iюмпонентами,
то все
эффективные
веI{ТОры
с
поло
жительными
Rомпонентами
лежат
в
выпуклой
оболочке
,
Л'
Л'
вектор-процессов
ai
\
составляющих
матрицу
А
.
Е.:4,
и
каждая
точка
этой
выпуклой
оБОЛОЧRИ,
лежащая
в
поло
жительном
ортанте,
является
эффективным
вектором.
ДОI{азательство
можно
найти
в
нниге
[41].
Тюшм
образом,
оказывается,
что
если
имеется
допус
тимый
план,
обеспечивающий
выпуск
I\аЖДОГО
продукта
с
избытком,
то
для
Rаждой
отрасли
имеется
определенный
производственный
процесс
(входящий
в
набор
л'),
позво
ляющий
получить
все
эффективные
векторы
с
положи
тельными
Rомпонентами
лишь
за
счет
перераспределения
трудовых
ресурсов.
Иными
словами,
любой
эффективный
план,
обеспечивающий
вьшуск
каждого
ПРОДУRта
с
избыт
ком,
либо
имеет
вид
{л',
и},
где
и
-
некоторый
осущест
вимый
вектор,
либо
ЭRвивалентен
плану
указанного
вида.
Сформулированное
утверждение
составляет
содержание
известной
в
математической
ЭRономике
теоремы
Саму
эльсона
о
замещении.
Подчеркнем,
что
этот
результат
получается
лишь
на
основании
анализа
свойств
множест
ва
эффективных
планов,
без
решения
вопроса
о
выБОj)е
конкретного
«оптимального»
плана.
В
приведенном
выше
числовом
примере
л'
= (1,
2)
и
любой
эффективный
план,
обеспечивающий
выпуск
каж
дого
продукта
с
избытком,
является
парой
{л',
и},
где
и
=
(U
l
,
u,z)
, 1/2.<
иl
< 3/4,
и2
=
1-
U
l
.
Из
рис.
2
можно
также
усмотреть,
что
сформулированное
утверждение
о
структуре
множества
эффективных
векторов
с
положи
тельными
компонентами
справедливо
в
силу
независи
мости
выбора
производственного
процесса
лi
Е
А;
для
каждой
i-й
отрасли.
5.
Большипство
методов
мпогокритериальной
оптими
зации
предусматривает
выделение
оптимального
решения
непосредственно
из
множества
всех
решений.
В
связи
с
этим
полезно
проанализировать
методы,
чтобы
выяснить,
всегда
ли
они
приводят
К
получению
эффективного
реше
ния,
и
если
нет,
то
специально
предусмотреть
возмож
ность
улучшения
выделяемого
решения
до
эффективного.
Для
иллюстрации
разберем
следующий
пример.
Б
[106]
был
изложен
оригинальный
метод
многокритери-
§ 1.5]
ЭНА
ЧЕНИЕ
понятия
ЭФФЕНТИВНОГО
РЕШЕНИЯ
45
аЛЬБОЙ
оптимизации
для
линейных
задач,
формально
состоящий
в
следующем:
вначале
находятся
ТОЧIШ
мак
симума
х
;
Е
Х
каждого
критерия
t.
в
отдельности,
а
за
тем
оптимальное
р~шение
х
О
получается
как
такая
выпук
лая
комбинация'
точек
x
i
(т.
е.
как
точка
вида
х(Л)
=
т
т
=
~
л'iХi,
где
л'i
>
О,
t =
1,
2,
..
'1
т,
~
л'i
=
1),
для
ко-
{=1
{=1
торой
максимальное
из
нормированных
отклонений
зна-
u t
'"
чении
критериев
I
от
соответствующих
максимумов
У!
=
=
ti
(x
i
)
минимально,
т. е.
у7
- f
i
(Х
О
)
•.
у7
- f
i
(х(Л»
тах
'''''
=
illln
тах
I
{ЕМ
У
i
Л
{еМ
I
у
7
где
М =
Н,
2,
...
,
т}.
'Указанное
определение
оптимального
решения
имеет
существенные
недостаТRИ.
Во-первых,
если
некоторый
критерий
пмеет
несколыю
точек
максимума
на
Х,
то
не
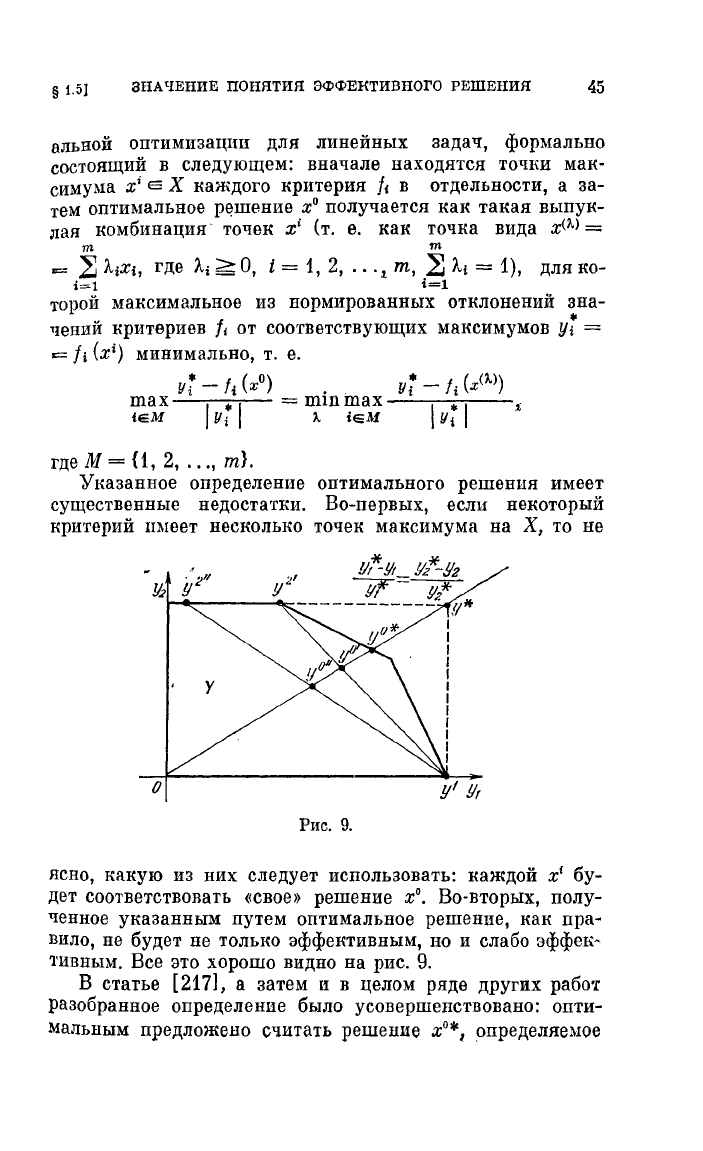
у
()
У/-!It
.у2
*-!/2
!/'
7=
У2*
------------
//*
Рис.
9.
I
I
I
I
I
I
I
I
I
I
I
I
!/I
!/,
ясно,
какую
из
них
следует
использовать:
каждой
х'
бу
дет
соответствовать
«свое»
решение
х
О
•
Во-вторых,
полу
ченное
указанным
путем
оптимальное
решение,
как
пра
вило,
не
будет
не
только
эффективным,
но и
слабо
эффек~
тивным.
Все
это
хорошо
видно
на
рис.
9.
В
статье
[217],
а
затем
и
в
целом
ряде
других
раБО'l
разобранное
определение
было
усовеРIПенствовано:
опти
мальным
предложено
считать
решение
хО*,
.определяемое

46
ОСНОВНЫЕ
ПОНЯТИЯ
И
ОПРЕДЕЛЕНИЯ
[ГЛ.
1
ИЗ
УСЛОВИЯ
в
§ 2.1
будет
показано,
что
решение
ХО*
всегда
слаб<t
эффективно,
а
если
оно
единственно
(с
точностью
до
экви
валентности
"'"
j),
то
И
эффективно.
Легко
проверить
TaK~
же, что
если
хо
не
является
слабо
эффективным,
то
ХО*
>-
jXO.
Это
положение
иллюстрирует
тот
же
рис.
9.
6.
Понятие
эффективного
решения
позволяет
не
толь
ко
усовершенствовать
некоторые
методы
многокрите
риальной
оптимизации,
но
и
лучше
понять
их
сущность,
а
тем
самым
и
уточнить
области
их
практического
при
ложения.
Для
примера
разберем
ШИрОНО
известный
метод
мно
гокритериальной
оптимизации
-
метод
главного
крите
рия.
Этот
метод
состоит
в
том,
что
исходная
многокрите
риальная
аадача
сводится
к
задаче
оптимизации
по
одно
му
критерию
//,
который
объявляется
главным,
или
основ
ным,
при
условии,
что
значения
всех
остальных
(второстепенных)
критериев
должны
быть
не
меньше
некоторых
установленных
величин
«(требуемых
уров
ней»,
(<пороговых
значений»
и
т.
п.)
t
j
,
т. е.
к
задаче
/LCx)
-+
шах
Х
е
Х;
/j'(x)~
t
j
,
i =
1,
2,
"',
т;
i
'*
l.
(1)
Оптимальным
считается
всякое
решение
ХО
этой
задачи.
Заметим,
что
такое
решение
всегда
является
слабо
эффек
тивным,
а
если
оно
единственно
(с
точностью
до эквива
лентности
""',),
то
и
эффективным
(см.
§ 2.1).
Для
лучшего
уяснения
существа
этого
метода
воспользуемС'я
следую
щим
простым
свойством
эффективных
решений,
которое
лешо
установить
рассуждением
«от
противного»
(см.
тео
рему
(2.1.5):
Если
решение
ХО
эффективно,
то
оно
является
единст
венным
(с
точностью
до
ЭI\Вивалентности
"'"
j)
решением
задачи
(1)
при
любом
фиксированном
leM
II
tj=/i(XO),
i =
1,
2,
...
,
т;
i'*
l.
Сформулированное
утверждение,
иллюстрируемое
рис.
10
(для
т
=
2,
l = 1),
сразу
позволяет
сделать
сле
дующий
:вывод:
выбор
любого
эффективного
решения
~O

§ 1.5]
3НАqЕни~
ttОНJlТИЯ:
ЭФФЕНТИШ!ОГО
р~mjшиJt
формальпо
эквивалентен
назначению
в
задаче
О)
t
i
=
=
ji(XO)
для
всех
i,
причем
в
качестве главного
можно
выбрать
любой
критерий.
Это
означает,
что
предвари
тельныЙ
выбор
одного
из
I,ритериев
в
качестве главного
еще
никак
не
уменьшает
свободы
выбора
оптималь
ного
решения,
тан что
на
званпе
«главный
крите
рий»
весьма
условпо.
Сле
довательно,
вопрос
о
вы
боре
главного
нритерия
следует
решать
тан,
чтобы
облегчить
назначение
ве
личиН
t;
для
ограничений
па
остальные
критерии.
Практически
обычно
Рис.
10.
указывают
серию
«IIаборов»
{t;}
пороговых
значений,
и
для
наждого
(<набора»
решают
задачу
(1)
(если
t
j
слиш
I,OM
вешши,
то
ограничения
в
(1)
могут
Оl,азаться
несов
местными).
Далее
на
основании
анализа
полученной
се
рии
значений
производят
он:ончательное
назначение
величин
t;,
чем
и
определяется
выбор
оитимального
решепия.
Процедура
назначения
серии
иороговых
величин
огра
Iшчеппй
и
расчета
соответствующих
значений
нритериев
фантичесни
производится
с
целью
получения
представле
нпя
о
наиболее
важной
области
множества
(слабо)
эффеR
тивных
оценон
при
помощи
ряда
отдельных
точек
А
за
тем
полученная
информация
обеспечивает
эвристичесний
выбор
оптимального решения.
Следовательно,
метод
главного
Rритерия
стоит
прантичеСRИ
применять
лишь
в
тех
случаях,
ногда
имеются
соображения
о
при
мерных
значениях
величин
t
j
(или
довольно
УЗRИХ
пределах
для
этих
величин),
позволяющие
ограничиться
рассмотре
нием
сравнительно
небольшой
части
всего
множества
(слабо)
эффеитивных
решений.
Сформулированное
свойство
дает
возможность
аналогичным
предложенный
Е.
С.
Вентцель
уступон
(см.
[85]).
эффеRТИВНЫХ
решепий
образом
исследовать
и
метод
последовательных
7.
Выше
было
ПОRазано,
что
понятие
эффеитивности
(оптимальности
по
Парето)
играет
фундаментальную
роль

48
ОСНОВНЫЕ
ПОНЯТИЯ
И
ОПРЕДЕЛЕНИfI
(ГЛ.
(
для
многоиритериальных
зада'l
припятия
индивидуаль
ного
решения.
Это
понятпе
является
весьма
важным
И
для
задач,
представимых
в
форме
многоиритериальных,
в
том
числе
задач
припятия
индивидуального
реПJения
в
УСЛОВИЯХ
РИСI{а
и
неопределенпости
(при
конечном
мно
жестве
ВОЗМОiЮ1ЫХ
состояний
<<Природы»).
Для
игрОВЫХ
задач
(особенно
для
иооперативных
игр,
групповых
реше-.
ний
И
арбитражных
схем)
велииа
роль
таюн:е
и
понятия
слабой
эффеитивности:
в
большинстве
aI,сиоматичесиих
систем,
введенных
для
определения
понятия
оптимального
решения,
требуется,
чтобы
это
решение было
слабо
опти
мальным
по
Парето
(или
же
слабая
оптимальность
по
Парето,
т.
е.
слабая
эффентивность,
является
следствием
других
аисиом).
Мы
не
будем
иллюстрпровать
уиазанные
положения
и
отсылаем
заинтересованного
читателя
и
соот
ветствующей
литературе
l16,
53, 56,
96].
Подчеринем
лишь
тот
фаит,
что
понятие
слабой
эффеитивности
может
оиазаться
полеЗНЫl\l
и
для
задач
припятпя
индивидуаль
ного
решения.
Действительно,
в
сложных
праитичесиих
задачах
фор
мирование
набора
иритериев
является
достаточно
труд
ной
проблемоЙ.
Поэтому
один
из
подходов
и
построению
веиторного
критерия
состоит
в
том,
чтобы
вначале
соста
вить
по
возможности
наиболее
полный
перечень
крите
риев,
и
лишь
потом
(возможно,
в
процессе
анализа
и
ре
шения
задачи)
ИСIШЮЧИТЬ
из
рассмотрения
<<лишние»
(не
существенные)
критерии.
В
связи
с
этим
вознииает
nо-
оХ
2
А
прос:
в
каком
отношении
на
ходятся
множество
решений,
эффективных
по
полному
набо
ру
критериев,
п
множество
ре
шений,
эффективных
по
остав
шемуся
набору.
Оказывается,
что
они
могут
находиться'
в
общем
положении.
Это
подтверждает
оХ,
следующий
нростой
пример.
Рис.
11.
При
м
е
р
2.
Пусть
множе-
ство
Х
-
это
плоский
пяти
угольник
(рис.
11),
а
полный
набор
критериев
состоит из
!t(X) = X
1
,
!2(Х)
=
Х
2
•
ДЛЯ
ЭТОГО
набора
множество
эффективных
решений
-
отрезок
АВ.
Если
же
отбросить
второй
критерий,
то
множество

§
1.(\]
СОВС'1'В:!ШНО
Й
подлинно
зффЕI\ти1зны1~
РЕlUЕНИf!
49
эффентивных
решений
по
1,
-
это
отрезон
ве.
Интерес
по
отметить,
что
если
из
Х
<шьшолотЬ»
точну
в,
то
мно
жества
решений,
эффентивных
соответственно
по
(/"
12)
и по
/,'
танже
<шишатсю>
этой
точни,
но
остапутся
внеш
не
устойчивыми
и
не
будут
пересенаться.
В
то
же
время,
нан
петрудно
проnерить,
всяnое
реше
uие,
слабо
эффеnтивuое
по
соnращеuuо,м,у
uабору
nрите
риев,
является
слабо
эффеnтивuы,м,
и
по
nолuо,м,у
uабору.
А
ПОСI<ОЛЬКУ
всякое
эффективное
решение
и
слабо
эффен
тивно,
то
приходим
К
тю<Ому
выnоду:
после
построения
наиболее
широкого
набора
I\ритериев,
I\ОТОРЫЙ
в
дальней
шем
может
подвергнуться
СОI\ращению,
следует
выделять
именно
множество
слабо
эффеКТIIВНЫХ
решений,
так
кан
если
некоторые
I<ритерии
будут
отброшены,
то
выделен
ное
множество
будет
содержать
все
исходные
решения,
эффективные
по
ОI{Qнчательно
принятому
набору
крите
риев.
8.
Все
вышеизложенное
поназывает,
что
понятие
эф
феI<ТИВНОГО
решения
действительно
оказывается
фунда
ментальным
для
теории
и
праКТИI<И
многокритериальной
ОПТИМIIЗ&ДИИ.
Остается
еще
заметить,
что
эффективные
решения
обладают
рядом
оригинальных
(не
присущих
ТОЧI\З111
МaI,симума
числовой
функции)
свойств,
и
поэто
му
представляют
интерес и
с
чисто
математической
ТОЧЮI
зрения.
§ 1.6.
Собственно
и
подлинно
эффективные
решения
1.
Исследования
ПОI,азыnают,
что
среди
эффективных
могут
встретиться
оцешш
(решения),
оказывающиеся
в
определенном
смысле
аномальными.
При
м
ер
1.
У
=
{у
Е Е
2
Iу,:::
-(УУ}.
Эффективные
оценки
образуют
часть
параболы
у,
=
-(У2)2,
лежащую
во
втором
lшадранте
(рис.
12).
К
эффективным
относится
и
оценка
уО
=
(о,
о).
Разности
координат
эффективных
оценон
у
и
уО
оказываются
равными
величинам
/).У2
=
=
У2
-y~
=
У2
>
О
И
/).Уl
=
Уl
-
y~
= -
(/).У2)2
<
о.
Следо
вательно,
если
перейти
из
ТОЧIШ
уО
В
достаточно
близкую
н ней
эффектпвную
точку
у,
то
будет
получен
выигрыш
первого
порядка
малости
по
второму
критерию
за
счет
проигрыша
второго
порядка
малости
по
первому
нрите-
4
в. В.
ПОДИIIОВСНИЙ,
в.
Д.
Ногин

50
ОСНОВНЫЕ
ПОНЯТИЯ
И
ОПРЕДЕЛЕНИЯ
[ГЛ.
1
рию.
Если
критерий
/1
не
считать
несравненно
более
важным,
чем
j2,
то,
по-видимому,
естественно
сог
ласиться
на
некоторое
увеличение
/2,
допустив
на
поря:
док
меньше
потери
по
jl.
Таким
образом,
оценка
уО
явля
ется
аномальной:
она
неустойчива
в
указанном
смысле,
у
вано
для
И
поэтому
соответствующее
ей
решение
не
может,'
вообще
го
воря,
претендовать
на
ОПТИ
мальное.
Рассмотренный
пример
пока
дУ2
зывает,
что
иногда
имеет
смысл
специально
выделять
эффек
тивные
оцении
(И
решения),
которые
лишены
подобных
не
желательных
свойств.
Первое
определение
такого
рода
эф
фен:тивных
решений,
назван
ных
собственно
эффективными
(proper e//icient),
было
дано
Рис.
12.
х.
Куном
и
А.
Таккером
[1"87].
Однан:о
оно
было
сформулиро
дифференцируемого
случая
и
связано
со
спе-
циальными
условиями
регулярности,
позволившими
по
лучить
необходимые
условия
оптимальности.
Для
общего
случая
определение
собственной
эффективности
было
предложено
А.
Джоффрпоном
[161].
Эффективная
оценка
у
О
называется
собственно
эффек
тивной,
или
оптимальной
по
Джоффриону,
если
сущест
вует
такое
положительное
число
е,
что
для
любых
i
Е
М,
У
Е
У,
дЛЯ
которых
вьшолпяется
неравенство
У!
>
y~,
инекоторого
j
Е
М
такого,
что
выполняется
неравепство
о
Yj
<
Yj,;
(Yi
-
y~)/(yJ
-
Yj)
<:
о.
(1)
(2)
(3)
Заметим,
что
поскольку
уО
эффективна,
то
если
суще
ствует
оценка
у,
для
которой
при
нен:отором
i
вьшолня
ется
неравенство
(1) t
то
ОQяза
тельно
найдется
номер
j,
