Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач

Подождите немного. Документ загружается.

§ 3.4)

ОЦЕННА

ЧИСЛА

эффЕнтивныx

ТОЧЕR

f71

динатами.

Точпая

верхняя

оцеlша

числа

!Р(У)I

дЛЯ

YI.a-

занного

случая

была

получена

В. Б.

Аленсеевым

[2],

Т.

М.

Виноградской

и

М.

Г.

Гафтом

[15],

а

таю-ке

М.

R.

Альбертьяпом

[3].

Их

результаты

изложены

в

пер

вом

пую{те

параграфа.

Во

втором

пункте

получена

точ

ная

~ерхняя

оценка

числа

I S

(У)

I

слабо

эффективных

точек.

Другой

подход

к

оцеш,е

количества

эффентивных

то

чен

-

вероятностный

и

состоит

в

том,

что

точки

у

Е

У

рассматриваются

нан

пезаВIIсимые

случайные

векторы.

Тогда

'Р(У)I

и

!S(Y)I

ОI,азываются

случайными

величи

нами,

и

мощно

искать

их

распределения

и

числовые

характеРПСТИI\И

-

математическое

ожидание,

дисперсию

и

т.

д.

В

предположении,

что

координаты

случайных

точен

у

Е'У

-

независимыIe

непрерывные

одинаново

рас

пределенные

величины,

этот

подход

реализовали

О.

Барн

дорф

-

Нилсон

И

М.

Собль

[5],

Б.

А.

Березовсний

и

С.

И.

Травкин

[7J,

Т.

М.

ВинограДСI\аЯ

[14],

Х.

Нэлпайн

и

А.

Гоулдинг

[128]

*).

Их

результаты,

насающиеся

),!а

тематичеСI{ОГО

ожиданпя

'Р(

У)!,

приведены

в

третьем

пуните

параграфа.

1.

Будем

рассматривать

случай,

когда

У

-

т-мерная

целочисленная

гиперпараллелепипедная

решетка:

у

=

У

1

Х

YzX

...

X

Ут,

(1).

где

У;

=

{О,

1,

...

, l.},

l.

-

натуральное

число,

t

==

1,

2,

•.•

...

,

m.

Наждое

множество

У

s;;;

У

содержит

!

р

(

У)'

эфФеКТlIВ

ных

точен.

Обозначим

через

w

наибольшее

IIЗ

всех

чи-

сел

'Р(

У)'

дЛЯ

всевозможных

У

g

У.

Число

w

называет

ся

шириной

множества

У,

частично

упорядоченного

от

ношением

iE;;.

Это

число

и

есть

исномая

точная

верхняя

оцениа

количества

'Р( У)'

эффективных

точек

для

У

s;;;

У.

Очевидно,

что

при

отыскании

w

Можно

ограничиться

рассмотрением

только

тех

множеств

У

s;;

У,

которые

со

стоят

из

несравнимых

по

~

точен,

т.

е.

для

которых

у

-=

Р(

У).

Такие

множества

называются

неаависиы:ыми.

*)

Случаю,

ногда

ТОЧIШ

у

Е

У

получаЮТСII

•

результате

иеаа

висимых

реалиааций

НОР;-'Iально

распределенного

случайного

век

тора.

посвящен

ряд

работ,

упааанных

в

[5] I

а

таЮRе

статьи

[38,

39,

48].

172

СТРУНТУРА

МНОЖЕСТВА

ЭФФЕКТИВНЫХ

РЕШЕНИЙ

[ГЛ.

3

Незаnисимое

мпошество,

содержащее

l()

точен,

называет

ся

маI<сималыlмM

незавпсимым

множеством.

Числовую

функцию

'I},

определенную

на

У,

назовем

весовой,

если

для

любых

у',

у"

е

у

из

у'

~

у"

следует

fJ(Y') -

'1}

(у

" )

~

1.

Последовательпость

точек

у\

уа,

•.•

•

..

,

у'

из

У

называется

цепью,

если

уl:<

у

2

:<

•••

:<

у"

Число

s

называется

длиной

цепи,

а

точка

у'

-

маI\СИ

мальной

в

цепи.

Отдельная

точка

является

цепью

ДШI

ны

1.

'I}-центром

цепи

yt,

у

2

,

"',

уЗ

будем

называть

чис

ло

'I}*,

определяемое

тю,;

при

s =

2t

+

1,

при'

s =

2С.

Цепь

назовем

'I}-центрированной,

если

'I}*

=

О.

Множество

У

допускает

симметричное

покрытие

це

пями

при

весовой

фушщии

'11,

если

его

можпо

разбить

на

цепи

так,

что:

1)

цепи

попарно

не

пересекаются

и

в

объединении

дают

У;

.

2)

если

yt,

у2,

...

,

у'

-

произвольная

цепь

из

разбие

НИЯ,

то

'I1(yi+l) = 11{yi) +

1,

j =

1,

2,

•..

, s -

1;

З)

все

цепи

11-центрированы.

Л

е

м м

а

1.

ПУСТЬ

У

дОnУС1>ает

СUМJ.tетрuчн,ое

nOl>pbl-

тие

цеnя.ми

при

весовой

фующuи

11.

Тогда

мн,ожество

W =

{у

е

У!

-1/2

~

l1(У)

< 1/2}

(2)

является

ма~СUJ.taЛЫlЫМ

н,еаависимым

мн,ожествО.i!t.

Д

о

к

а

з

а т

е

л

ь

с

т

в

о.

Пусть

q -

число

цепей

в

сим

метричном

покрытии.

Так

как

любое

независимое

мно

}!,ество

У

с У

имеет

на

каш~ой

цепи

не

более

одной

точки,

то

ш;а

q.

С

другой

стороны,

в

силу

условия

2

из

определения

симметричного

поирытия

любые

две

точки

иа

W

несравнимы

по

~,

и поэтому

l()

~

I

WI.

Следова

тельно,

I

WI

:iii w S

q.

Из

определения

симметричного

понрытия

видно,

что

каждая

цепь

содержит

ровно

одну

точну

ИЗ

W,

таи что

IWI

=-

q.

Поэтому

ш"""

IWI

.•

§ 3.4]

ОЦЕННА

ЧИСЛА

ЭФФEI,ТИВНЫХ

ТОЧЕН

173

л

е

м м

а

2.

Мн,ожество

У

дОnУС1Оает

сuм,,;четрuчн,ое

n010pьtTиe

цепями

при

m

!I

(у)

=

~

f)i (Yi),

i=l

(3)

гОе.

'I'\;(Yi) =

-и2

+ Yi, i =

1,

2,

...

,

m.

(4)

Доказательство

проводится

индукцией

по

pa3MepHO~

стн

m.

При

т

= 1

множество

У

=

У

1

ПОRрывается однои

цепью

О,

1,

...

,

["

прпчем

условия

2

11

3

из

определения

симметричного

ПGНрЫТIIЯ,

очевидно,

выполняются.

Допустшr,

что

утверждение

о

возможности

симмет~

РПЧIIОГО

ПОНрЫТИЯ

f

при

(3)

верно

для

HeRoToporO

т

=са

= k - 1

е:;

1,

и

покаа,ем,

что

оно

верно

и

для

т

=

k.

Введем

обозначения:

,

Y1XYzX",

xYj

=

УШ,

~

f)i = f)i, j = k

-1,

k.

i=l

ДЛЯ

I,ЮIЩОГО

j

Е

У

л

мпоа;ество

УfЛ-II

Х

{Л

-

это

co~

НОI,УПНОСТЬ

всех

пар

ВIlда

(yk_"

Л,

где

у"-I

=

CYI,

Yz,

•••

•

..

, Yk-I)

Е

Ylk-I].

Поэтому

СJlМ'lетрпчпое

ПОI,рытие

цепя~

ми

МПО,I\ества

yfk-II,

существующее

по

предполоа;ению

при

'1'\"-1,

индуцирует

ПOI;РЫТIIе

и

множества

yf

k

-

1

1

Х

{j}

цепями,

обладающее,

очевидно,

cBoiicTBaMII 1

и

2

сим~

метричного

ПОНрЫТIIЯ.

Однако

цеШI

I1ндуцированного

по~

КрЫТИЯ

не

являются

'l'\R-центрированньши:

для

них

!l

h

* =

n(k-l)*

+ 'l'\h

и)

=

О

+

'!1п

(п

=

nk

и).

(5)

Рассмотрим

МНО,l\ества

Y[k-I]

Х

{О},

У[Л-II

Х

{Н,

•••

,

У[А_I

I

Х

{lл}.

Так

как

покрытие

цепями

миожесТ.II

Yfk-I]

Х

{Л

построено

по

одному

и

тому

же

ПРИНЦllПУ,

то

каждой

цепи

из

любого

множества

yfk-I]

Х

{j}

соот

ветствует

некоторая

цепь

во

ВСЯI\ОМ

множестве

YfA-1

J

Х

Х

{r},

r=l=

j.

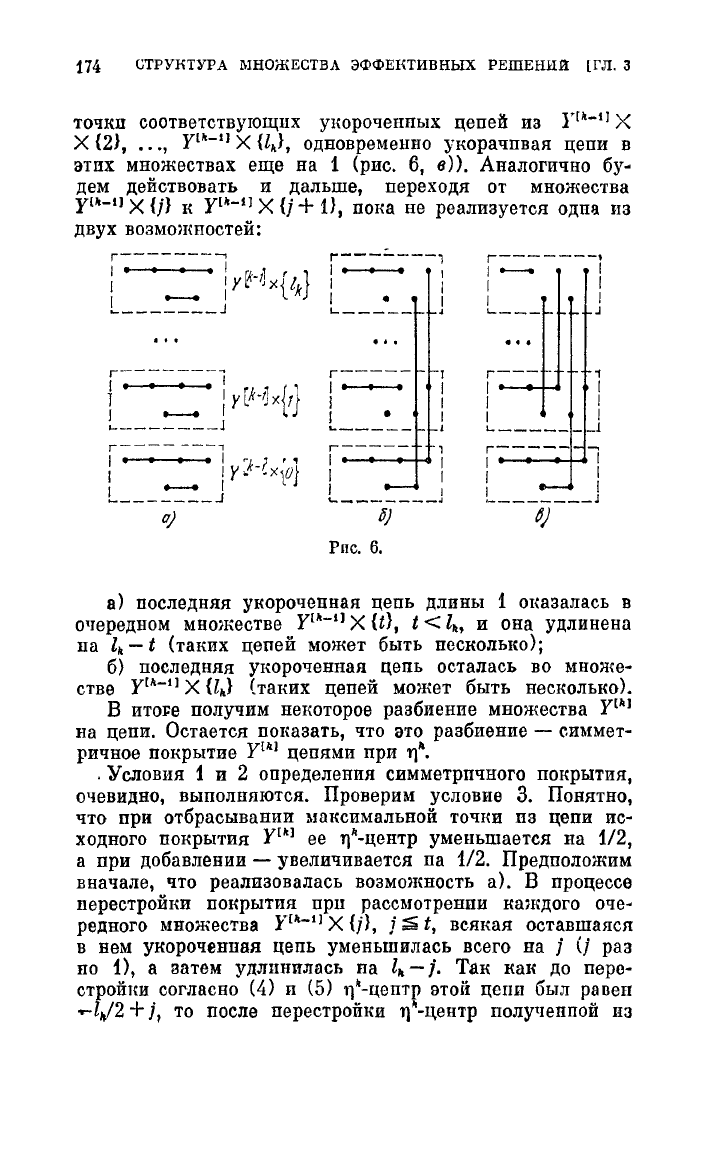
Это

условно

изображено

на

рис.

6,

а).

"Удлиним

КЮI\ДУЮ

цепь

из

yfk-I]

Х

{о}

на

[А,

добавив

R

ней

МaI{сималъные

точки

всех

соответствующих

ей

цe~

пей

из

Y[A-I]

Х

{1},

•..

,

У[А-

II

Х

Н

Io

}'

одновременно

YKopa~

чивая

все

цепи

в

неречисленных

мношестnах

на

1

(рис.

6,

6».

Далее

УДЛИПП1\1

Rаждую

укорочепную

цень

ИЗ

yr

~-I

I

Х

{Н

на

1"

-

1,

добавляя

1<

вей

МaI,симаЛЬНЫ8

174

струнтур

А

МНОЖЕСТВА

ЭФФЕНТИВНЫХ

РЕШЕНИЙ

[ГЛ.

3

точки

соответствующих

УI\ороченных

цепей

из

уrЛ-I]

Х

Х

{2},

•..

,

yt~-I]

Х

{lл},

одновременно

укорачпвая

цепи

в

этих

множествах

еще

на

1

(рис.

6,

в».

Аналогично

бу~

дем

действовать

и

дальше,

переходя

от

множества

Y(~-I]

Х

{j}

К

Y[~-I]

Х

{j + 1},

поиа

не

реализуется

ОДНIl

из

двух

возможностей:

г-------.....,

r---=----,

l'

,1

rk~

}

1,

•

I

lyr~x[4

I

1--.1

l

1.

~

_______

J

~

____

_

г-------~

1.

• • , I r "

{}

1 1

y~.IJX

f

J

-1

...

________

]

г----

---,

1'.

• I

СК?

"

I

'У"-'Х1

0

1

1

--

I -

~

_______

J

а)

г-----

I

--.-.-.

!

I •

'------

r------

I

I

I I

~--_._---,.j

о)

PIIC.

6.

г-------,

1-

I

I I

1 I

,-___

.J

...

г---

. 1

1 I

I I

1 I

'-

_______

1

г-----

-

I I

i

---

I

•

________

J

()

а)

последняя

укороченная

цепь

длины

1

OI\азалась

в

очередном

множестве

Y(~-I]

Х

{О,

t <

lk'

И

она

удлинена

па

lk

- t

(таких

цепей

может

быть

несколыи);

б)

последняя

уиороченная

цепь

осталась

во

множе·

стве

yr.\-I]

Х

{lл}

(таиих

цепей

может

быть

несиолько).

В

ито~е

получим

неноторое

разбиение

множества

yr

k

]

на

цепи.

Остается

ПОI\азать,

что

это

разбиение

-

симмет~

ричное

ноирытие

ущ

цепями

при

'1'\"

•

.

Условия

1

и

2

определения

симметрпчного

понрытия,

очевидно,

выполпяются.

Проверим

условие

3.

Понятно,

что

при

отбрасывании

мансимальной

точии

из

цепи

ис~

ходного

поирытия

ущ

ее

Тjk_центр

уменьшается

на

1/2,

а

при

добавлении

-

увеличивается

па

1/2.

Предположим

вначале,

что

реализовалась

возможность

а).

В

процессе

перестройии

покрытия

при

рассмотрении

иаiRДОГО

оче

редного

множества

Y[I·_I]

Х

{Л,

j:i!

t,

всякая

оставшаяся

в

нем

укороченпая

цепь

уменьшилась

всего

на

j

(j

раз

но

1),

а

затем

УДЛIIнилась

па

1"

-

j.

Так

как

до

пере

стройтш

согласно

(4)

и

(5)

чk-цептр

этой

цепи

был

равен

..,..1,/2

+

j,

то

после

перестройии

'l'\k_центр

полученпой

ИЗ

§

34]

ОЦЕННА

ЧИСЛА

ЭФФIЖТИВНЫХ

ТОЧЕН

f

75

нее

цепи

равен

11>.

1

lh-j

-

Т

+ f -

"2

+ 2 =

о.

Таким

обраЗО~I,

ВСЯI,ая

цепь

покрытия

является

ч~-цент~

рированноЙ.

Предположим,

наконец,

что

реализовалась

возмож

JIOСТЬ

б}.

Точно

так

же,

как

и

в

предыдущем

случае,

проверяется,

что

всякая

цепь,

полученная

из

цепей

мно

жеств

Ylh-11

Х

{Л,

j <

l~,

является

ll"-цеНТРИIюванноЙ.

Остается

рассмотреть

УJюроченные

цепи

из

yI"-1]

ХНА}'

КаiIщая

такая

цепь

была

получена

из

неJtоторой

исход

ной

цепи,

ч"-цептр

I\ОТОРОЙ

согласно

(5)

и

(4)

был

равен

ln/2,

укорачиванием

1"

раз

на

1.

Следовательно,

ее

'1')"-

центр

равен

1,,/2

-1,,/2

=

О,

т. е.

она

центрирована

.•

Согласно

лемме

1

множество

(2)

является

мансималь

ньш

независимым

множеством.

Для

весовои

функции

(3)

условие

-1/2::::;; 'I')(y} < 1/2

равносильно

УСЛОВIIЮ

Yl

+

У2

+ ... +

Ут

=

Ent

[

4-

~

li J

(6)

где

через

Ent

[zJ

обозначена

целая

часть

числа

z.

Это

означает,

что

искuмое

число

ZlJ

= !

W!

равно

числу

N

m

(lI'

12

•...

,

1т}

цеJlочисленных

решении

уравнения

(6)

при

ограничешlЯХ

о;:§;

Yt

~

lj.

t =

1,

2

•...•

m.

(7)

Итак,

доказана

Т

е

о

р

е

м

а

1.

Для

nроизвОЛЬ1l0го

множества

У

5

У

справедлива

точная

oцeH~a

Чпсло

N

m

(ll.

12

•...•

1т}

согласно

(6)

и

(7)

на

языке

номбинаторного

анализа

можно

интерпретировать

кан

число

способов

раЗМЕ'щения

n =

Ent

[ +

i~

lJ

одинако

вых

предметов

по

т

различным

лчейнам,

причем

емность

t-и

ячеини

равна

1

•.

Следовательно,

это

число

равно

коэф

фициенту

при

[n

В

разложеНlIП

ПРОПЗDодящеii

функцпи

f

76

структур

А

МНОШЕСТВА

ЭФФЕI,ТIIВНЫХ

РЕШЕНИй

[ГЛ

3

вида

[911:

т

F

ти;

11'

'2'

...

,

lт)=

П

(1

+ t + ... + t

1i

).

(9)

i=1

Для

вычисления

числа

Nm(ll,

1a,

••• ,

1т)

в

[15]

при·

ведена

довольно

слощная

формула.

Там

же

указано,

что

в

случае

/1>=

/а

=

...

=

1т

= 1

число

Nm(l}

-

Nm(l,

••• ,

1)

:может

быть

найдено

подсчетом

ноэффициента

при

t",

где

n =

Ent

[1/2],

в

ра3ЛОil,еНIIИ

ПрОllзводлщей фУННЦUII

[см.

(9)]

F".(t;

l)=(1+t+

...

+t

1

)m

или

вычислено

по

фОР)1уле

([91],

с.

126):

т

N

т

(1)

=

~

(-

1)Т

С~nС~;~:А~-J;.U+l)-l

=

т=о

v

~1

(

1)Т

С

Т

Cn-r(l

+1)

=

.:;о

-

111

m+n-T(I+l)-l,

(10)

T~O

где

'V

=

Епt

r 1

~

1].

В

частности,

если

1 =

1,

т. е.

если

у

-

булев

т-мерный

нуб,

то

n =

Ent

[

~]

и

формула

(10)

указывает

хорошо

известное

выражение

для

шири

ны

Т8НОГО

куба

в

этом

легко

убедиться,

если

учесть,

что

N m ( 1) -

ноэф

фициент

при

t

n

в

разложении

производящей

фующип

P,,,(t;

1)-(1+t)т.

2.

Перейдем

к

рассмотрению

слабо

эффеr{тивных

то·

чек.

Будем

по-прежнему

считать,

что

У

-

т-мерная

це·

ночисленная

решетка

(1).

Т

е

о р

е

м

а

2.

Для

nроusвольного

)tножества

У

s=

У

сnраведЛllва

точная

оценха

т

т

1

8

(У)

I

~П

(lj

+

1)

-

П

lj.

(11)

'-l

j-l

ОЦЕННА

ЧЙСЛА

ЭФФЕI\ТИВНЫХ

ТОЧЕН

177

д

о

к

а

з

а т

е

л

ь

с

т в

о.

Введем

вю,торное

н;ение

• :

~Y

-+

у

по

СJlедующему

правилу:

отобра~

({

(у

l'

У2'

.•.

,

Уm)

= (Yl+

min

(li -

У1)'

(еМ

Y'J

+

min

(li -

у,),

...

,

Уm

+

min

(1;

- Yi»'

(ем

leM

Если

для

неноторого

i

Е

1VI

выполнено

У,

=

1"

то

m

iп

и;

-

У1)

=

О

и

't

(Yl'

У2'

•..

,

Уm)

=

(Yl'

Yz,

.••

,

Уm).

Дa~

iE.'l

лее,

из

определения

отображения

't

следует,

что

дЛЯ

ЛIO~

бого

У

s;;

У

Jlшожество

't

(У)

= U

't

(у)

состоит

иа

точек,

lIеУ

по

крайней

мере одна

координата

.которых

принимает

свое

наибольшее

значение

(у,

=

1;

для

неноторого

j

Е

АЛ.

Поэтому

все

точки

mhoJ-нества

't

(У)

несравнимы

между

собой

по

отношению

>.

Кроме

того,

если

двум

раЗЛИ'I~

ньш

точнам

У',

УЗ

Е

У

соответствует

одна

и

та

те

точка

11З

.(

У),

то

либо

у'

>

yi,

либо

уЗ>

yi.

Следовательно,

дЛЯ

ПРОIIЗВОЛЬНОГО

мнощества

У

s;;

У:

IS(Y)I

;;;;

Iт(У)1

~

Iт(У)1

=

т.

Понятно,

что

Т

-

это

число

тех

точек

из

У:

у

HOTO~

рых

по

I\райней

мере

одна

координата

ПРИllюraет

свое

наибольшее

значение.

Найдем

это

число.

Решетна

У

co~

m

держит

П

(11

+

1)

точек.

А

число

точек,

ни

одна

из

HO~

i=l

ординат

I\ОТОРЫХ

не

принимает

своего

наибольшего

8Ha~

m m m

чения,

есть

П

1i.

Поэтому

Т

=

П

(l!

+

1)

-

П

1,

.•

1=1

1=1

i=l

Если

l;

....

1,

t =

1,

2,

...

,

т,

то

(11)

принимает

вид

IS«Y)I

~

(l

+

1)>n

_zm.

Отсюда

в

частном

случав

1 = 1

(т.

е.

IЮГl\а

НООРДlIнаты

точеI~

у

являются

булевыми)

получаем

IS(Y)I:1ii

2т

-1-11'1-1.

Эта

оцею,а

очевидна:

в

булевом

т-мерном

гипернубе

не

является

слабо

эффвнтивной

лишь

одна

точr;а,

все

r;oop~

ДИНIIТЫ

которой

-

нули.

12

в.

в.

ПО.:\>JНОЕСJШЙ,

В

Д

HvrlI!l

178

CTP~'HT~'P

А

l\ШОЖЕСТВЛ

ЭФФIШТИВНЫХ

РЕШЕНIIй

(ГЛ.

3

3.

Рассмотрим

следУЮЩУЮ

вероятностную

модель

ге-_

нерирования

конечпого

множества

У

с:

Ет,

содержащего

N

точек.

Пусть

У

-

случайный

вектор,

компоненты

кото

рого

YI,

У2,

••.

,

Уm

-

независимые

случайные

величины,

и

F,

-

функции

распределения

У/.

Точки

Yt,

Уz,

•.. ,

уН,

п{)лученные

в

результате

реализаций

вектора

fJ

(т.

е.

яв

ляющиеся

выборной

N

значений

этого

вектора),

И

обра

зуют

множество

У.

Следовательно,

числа

'Р(У)I

И

IS(Y)I

эффективных

И

слабо

эффентивных

точен

этого

множест

ва

оказываются

случайными

величинами.

Наша

цель

сос

тоит

в

исследовании

и

получении

формул

для

математи

ческих

ожиданий

этих

случайных

величин.

Будем

предполагать,

что

все

функции

распределения

F,

непрерывны.

Тогда

nероятность

того,

что

две

одноимен

ные

ноординаты

произвольных

точен

У

;

II

Y~

совпадут

(т.

е.

при

неноторых

j

=1=

k

и

i

ОI\ажется

справедливым

.

k)

.

равенство

y~

=

Yi

равна

нулю.

Отсюда

следует,

что

числа

эффeI{ТИВНЫХ

и

слабо

эффентивных

точек

множества

У

равны

почти

наверное,

так

что

Е

[1

Р

(У)

1]

=

Е

[ I S (Y)IJ.

Поэтому

в

дальнейшем

будем

вести

речь

лишь

о

случай

ной

величине

'Р(

У)

1.

I\pOMe

того,

из

непрерывности

фушщий

F,

следует,

что

достаточно

ограничиться

рассмотрением

случая,

когда

.

М

1 2 N

при

каждом

l

Е

компоненты

Yi, Yi,

...

,

Yi

можно

стро-

го

ранжировать,

т. е.

записать

равенства

.1i'2

jN

(12)

Yi

>

Yi

> ... >

Yi

,

где

<JI,

J2,

•.. ,

jN)

-

некоторая

перестановка

множества

{1,

2,

•..

,

N}.

Следовательно,

каждой

ТОЧ1\е

У

;

можно

по

ставить

в

соответствие

ранговый

вектор

ri,

где

r{

-

ранг

номпоненты

uj

в

(12),

т.

е.

номер

занимаемого

ею

мес

та,

отсчитываемый

справа.

Например,

если

при

N = 3

11

i = 2

неравенства

(12)

имеют

вид

y~

>

y~

>

У:,

то

r~

= 3,

r'~

=

2,

r~

=

1.

Нетрудно

понять,

что'

для

выделения

Р(У),

а

значит

11

для

подсчета

числа

IP(Y)I,

достаточно

знания

не

самих

точек

yj,

а

лишь

ранговых

векторов

r.

Поскольну

точки

y~

являются

реализациями

одной и

той

же

случайной

величины,

то

из

соображений

симметрии

ясно,

что

вероят

ность

получеНIIЯ

любой

перестаНОВКII

<JI,

J2,

••.

,

!н>

I

соот-

ОЦЕННА

ЧИСЛА

ЭФФЕНТИIЗНЫХ

ТОЧЕН

179

ветствующей

неравенствам

(12)

ПрИ

произвольно~[

фик

сарованном

i

Е

М,

одна

и

та

те

и

равна

j~

l'

Отсюда

сразу

следует,

что

вероятность

события

r1

= lt

для

этого

i,

где

k -

произвольное

заданное

число

из

{1,

2,

•..

,

N},

равна

;.

•

Все

это

означает,

что

распределение

случайноii

пеличины

I

Р(

у)

I

не

зависит

от

Iюнкретного

вида

распре

делений

случайных

величин

У!

(т.

е.

вида

функций

Fj )

п

опредедяется

лишь

числами

т

1I

N.

Поэтому

для

матема

тического

ожидания

числа

эффективных

точек

Е

[ I

Р

(У)

1]

можно

ввести

обозначепие

E.v(m).

т

е

о

р

е

м

а

3.

Справедливо

СООТ1l0Ulеnие

N

E

N

(т)

=

l:

;,-

Е"

(т

-

1),

E

N

(1)

=

1.

(13)

1<=1

д

о

к

а

з

а т

е

л

ь

с т

в о

[128З.

Тю\

паI,

вероятность

вы

полнения

равенств

уу

=

У1,

p=/=k,

для

точеl{

из

У

равна

ну-

б

1 2 N

лю,

то

удем

полагать,

что

коордипаТЫУi,

Yi,

.•.

,

У;

попар'

но

различны

и

=

1,

2,

...

,

т).

ПОСI\ОЛЬНУ

число

эффет\тивпых

точен

не

меняется

от

перепумерации

точен

множества

У,

то

l\ЮЖНО

счптать,

что

1 > 2 > > N

Уm Уm

.•.

Уm.

(14)

Поэтому

при

т

=

1,

очевидно,

EN(m)

=

1.

Рассмотрим

случай

т>

1.

Обозиачим

через

p(N,

т)

вероятность

того,

что

наугад

выбранная

ТОЧI,а

из

У

эф

феI\тивна.

Нан

уже

отмечалось,

вероятность

наугад

вы

бранной

ТОЧRИ

из

У

быть

k-и

в

(14)

(т.

е.

y

h

)

равна

1/N.

В

.

zi

()

j

j)

ведем

в

рассмотрение

BeI,

торы

=

у

1,

У2'

•••

,

у

т-l

,

j=1,2,

...

,N.B

силу

(14)y~>ytn

приj=k+1,

...

,N

; k

Н

У1ll

>

Ут

при

j =

1,

...

, k -

1.

Следовательно,

y~

эффеI\-

тивна

в

том

и

ТОЛЫЮ

TO~I

случае,

если

веI\ТОР

z~

эффы\

тивен

во

множестве

{zt,

z2,

...

,

Zh}

с:

Е"'-'.

А

вероятность

пос.lIедпего

события

есть

р

(k,

т

- 1).

Следопательпо,

ве

роятность

того,

что

точка

пз

У,

выбранпая

паугад,

бу

дет

k-й

и

эффеI\ТИВПОЙ,

равна

p(k,

т

-

1)/N.

Поэтому

12*

180

СТРУ!{ТУРА

l\шо;r;ЕСТВА

ЭФФЮ\ТИВНЫХ

РЕШЕНИй

[ГЛ.

Э

по

формуле

полной

вероятности

N

р

(Н,

т)

=

~

~

р

(k,

т

- 1).

It=l

(15)

'УЧТЯ,

что

E

N

(т)

=

Np

(N,

т)

JI

ЕА(m

- 1) = kp(k.

m-

- 1), k =

1,

2,

.•

"

N,

из

(15)

сразу

получаем

(13)

••

При

помощи

(13)

для

небольших

N

и

т

можно

лешо

подсчитать

среднее

число

эффеI{ТlШНЫХ

решений.

:Когда

N

велико,

вычпслепие

среднего

значения

услож

о

няется.

Для

т

= 2

из

(13)

получаем

следующую

асимпто

тичеСI{УЮ

формулу:

N

E

N

(2) =

~

i

,....

ln

N +

С,

п=1

где

С

= 0,5772 ... -

ПОСТОЯПfiая

Эiiлера.

Таким

образом,

среднее

чпсло

эффективных

точек

в

случае

т = 2

растет

J\aI\

патуральпый

логарифм

числа

N.

Если

т

=

3,

то

песложно

провеРIlТЬ

справедливость

следующей

асимптотпчеСIЮИ

оценки:

при

N

-+

00;'

Вообще,

для

фШ{Сllроваппого

т

прп

N

-+

00

имеет

мес

то

формула

(см.

[5, 7]):

E

N

(т)

ro./

(т

~

1)!

ln"'-lN,

которая

свидетельствует

о

том,

что

среднее

число

эффеI{о

тивных

точек

растет

х.ю{

(т

- 1

)-я

степень

натурального

логарифма

числа

N

допустимых

решений.

Эту

формулу

можно

использовать

для

приближенной

оцеюш

числа

эф

фективных

точен,

если

N

достаточно

велико.

Т

е

о

р

е

м

а

4.

Справедлива

точная

формула

N--l

11

Е

N

~

111

C

N

-

1

N

(т)

=

~o

(-

)

(k

+

1)т.

(16)