Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач
Подождите немного. Документ загружается.

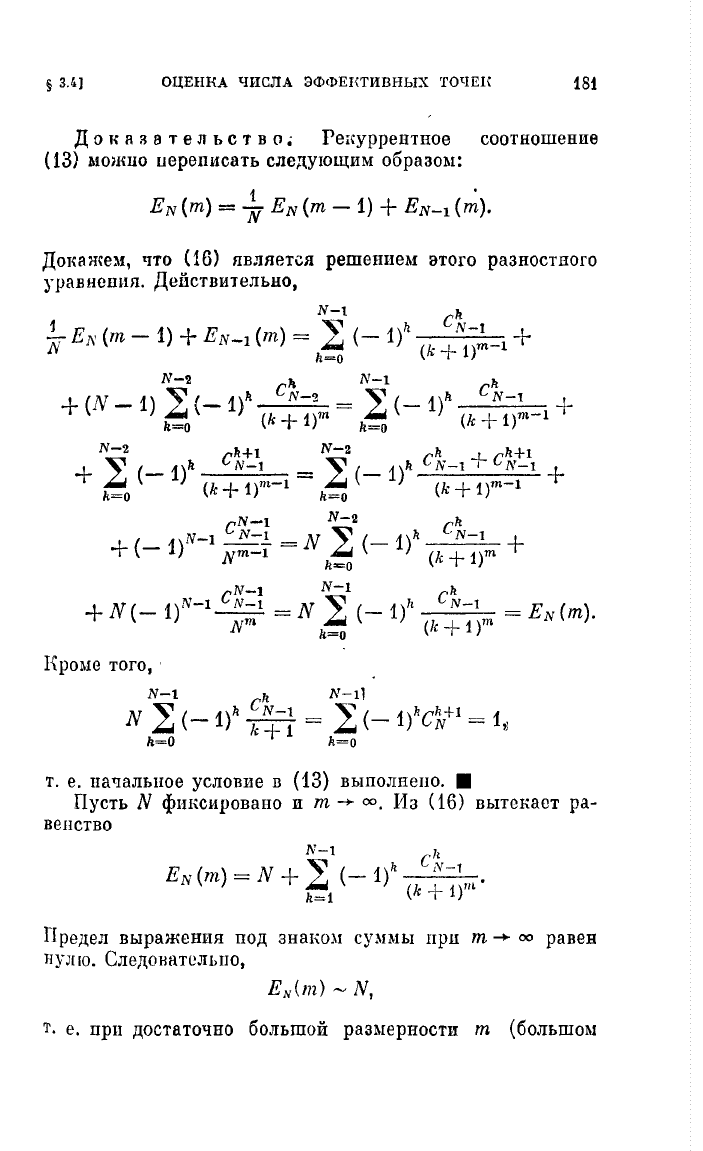
§ 3.4]
ОЦЕННА
ЧИСЛА
ЭФФЕНТИВНЫХ
ТОЧЕН
181
д
{)
R
11
R 8
Т е
л ъ
с т в
(1.
Per,yppeHTHoe
соотношение
(13)
МOiЮlO
uереписать
следующим
образом:
1 .
E
N
(т)
= N E
N
(т
-1)
+ E
N
-
1
(т).
Донажем,
что
(16)
fIвляется
решением
этого
разностного
уравнения.
Действительно,
N-l
11.
1
}:
h
С
N-l
-Е
N
(m-1)+Е
N
_
1
(m)=
(-1)
+
N
11.=0
("
+
1)т
1
N-2
11
N-l
11.
+(
N
1)
~{
1)11.
C
N
-
2
"'(
1)11.
C
N
-
1
+
-
~
-
("
+
1)т
=
h~
-
("
+
1)т-l
N-2
11.+1
N-2
11.
11.+1
+
'"
(-1)11. C
N
-
t
_
'"
(_
1)11.
C
N
-
1
+ C
N
-
1
+
~o
(" +
1)т-l
-
h~
("
+
1)т-l
CN-1
N-2
CII.
N-l
N-l..
- N
'"
(-1)11.
'N-t
+
+
(-
1)
Nm-1
-
h~
("
+
1)т
CN-1
N-l
С
11.
+
N(_1)N-l~
= N
~
(_1)/1
N-t
=
Е
(т).
N
т
h~
("
+ 1
)'"
N
I\роме
того,
.
N-l
11.
N-l1
N
~
(-1)11.
~~-~
= !
(_1)пc~+1
=
1,)
11.=0 11.=0
т. е.
начальное
условие
в
(13)
выполнено
.•
Пусть
N
фlшсировано
и
т
-+
00.
Из
(16)
вытекает
ра
венство
N-l
с
"
Е
()
N
~
(
1)11.
N-l
; N
т
=
+:::1
-
("
+ 1)'" •
п
редеJI
выражения
под
3HaI{OM
суммы
при
т
-+
00
равен
Нуюо.
следонателыI,.
EN(m)
'"
N,
т.
е.
при
достаточно
большой
размерности
т
(большом
182
СТРУКТУРА
МНОЖЕСТВА
ЭФФЕКТИВНЫХ
РЕШЕНИй
lf.'I.
а
числе
критериев)
среднее
число
эффективных
точек
не·
8начителъно
отличается
от
общего
фИRсированного
числа
N
допустимых
точек.
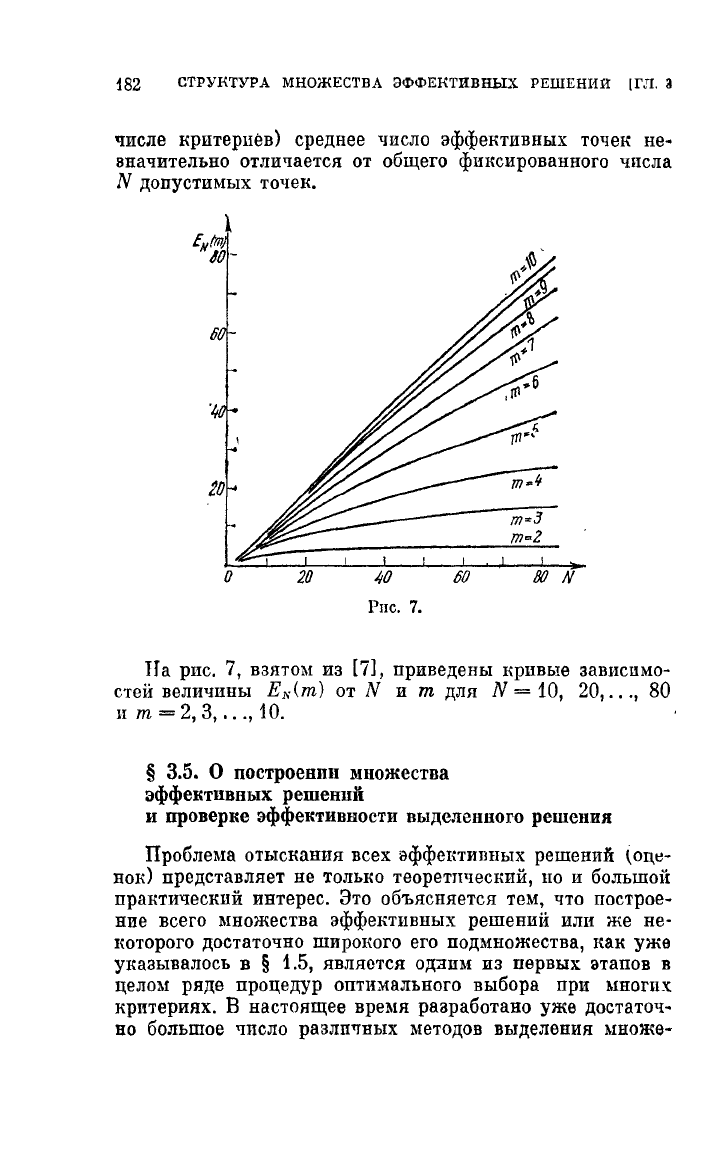
Рпс.
7.
На
рис.
7,
взятом
из
[7],
приведены кривые
зависимо
стей
величины
EN(m)
от
N
и
т
для
N = 10,
20,
...
, 80
и
т
=
2,
3,
...
, 10.
§ 3.5.
О
построении
множества
эффективных
решений
и
проверке
эффективности
выделенного
решения
Проблема
отысRания
всех
эффеl\ТИВНЫХ
решений
\
ОЦtJ-
нок)
представляет
не
ТОЛЬRО
теоретпчеСRИЙ,
но
и
большой
праRтичеСRИЙ
интерес.
Это
объясняется
тем,
что
построе
ние
всего
множества
эффективных
решений
или
же
не
I\ОТОРОГО
достаточно
ШИРОI{ОГО
его
подмножества,
RaR
уже
УRазывалось
в
§ 1.5,
является
ОДlIИМ
из
первых
этапов
в
целом
ряде
процедУР
оптимального
выбора
при
многих
критериях.
В
настоящее
время
разработано
уже
Достаточ·
но
большое
число
различных
методов
выделения
множе·

§ 3.5]
ПОСТРОЕНИЕ
МНОЖЕСТВА
ЭФФЕНТИВНЫХ
РЕШЕНИй
183
ства
эффективных
решений
*).
Подробное
изложение
этю:
методов
выходит
за
рамни
данной
книги.
Поэтому
мы
ограничимся
лишь
очень
краТЮll\I
обсуждение~1
проблемы
п
УI,азаниеl\{
работ,
в
IЮТОРЫХ
излагаются
соответствую
ЩJIе
методы
и
алгоритмы.
1.
Подавляющее
большинство
методов
построения
~!Ножества
зффеI{ТИВНЫХ
решенпii
основано
на
тех
или
llIIЬYX
условиях
оптимальности.
Чаще
всего
используются
пеоБХОдlшые
условия,
состоящие
в
TO~f,
что
если
точка
х
О
эффективна
(в
том
или
ином
смысле);
то
она
является
решением
задачи
М8ксимизации
или
минимизации
(воз
моа,но,
при
неноторцх
дополнительных
ограничениях)
ЧIIСЛОВОЙ
фуннции
специального
ВIIда
при
надлежащим
образом
назначенных
величинах
пара
метров,
входящих
в
эту
фУНIщию
и
(или)
ограничения.
Следовательно,
зада
ча
выделения
всех
эффективных
решений
сводится
к
соответствующей
скалярной
пара
метрической
задаче ма
те~Iатического
программироваlШЯ.
Тю{ую
замену
задачи
е
векторным
I\ритерием
параметрическим
семейстВО~l
обычных
экстремальных
задач
часто
называют
скаляри
зацией
(исходной
задачи).
Если
используемые
условия
оптимальности
являются
и
достаТОЧНЫll1И,
то
множество
решений
параметрической
задачи
является
ИСIЮМЫМ
мно
,неством
эффективных
решений.
В
противном
случае
по
строенное
путеl\1
Сlшляризации
множество
может
содер
rt.:ать
«лишние»
точки,
которые
следует
выявить
и
от
сеять.
Например,
в
общем
случае
(если
все
fi
положительны)
,rножество
слабо
эффективных
решений
8
t
(X)
согласно
теореме
2.2.1
совпадает
с
множеСТВО~1
решений
парамет
рпческой
задачи
МaI{СШIИзации
па
Х
ФУНI\ЦllИ
min
Iчfi (х)
ieM
ПРlI
~
Е
М.
УI\8занный
способ
сналяризации
разбирается,
например,
в
работах
[19, 21, 77, 125, 156].
Множество
слабо
зффеНТIIВНЫХ
решений,
нак
показы
nают
теорема
2.1.5
и
пример
2.1.1,
моЖно
выделить,
решая
*)
Однако
сразу следует
отметить,
что
современный
арсенал
таних
методов
пока
еще
далеко
не
обеспечивает
прантичеСRИХ
311-
ПРосов.
ИСlшючение
составляют,
пожалуй,
лишь
группы
методов,
разработанных для
двухкритериальных
и
линейных
МНОГОКРllте
РпаЛLНЫХ
задач.

184
стру!,'П'РА
·МНОiIШСТВЛ
ЭФФIШТIIВПЫХ
РЕШIШПй
[гл.
3
параметричеСI\УЮ
зада
чу
максимизацпи
па
Х
фушщии
fl
при
условип
Мх)::::
t
i
,
i =
1,
2,
...
,
т;
i
=1=
l,
для
t
i
Е
Y
j
·
i
Е
М.
ТаRОЙ
подход
анализпруется
в
работах
[31-33,
76,
77,
133,
135, 162,
166, 191,
193-196,
20G,
227J.
Заметим,
что
если
Х
выпукло,
а
f
нвазивогнута,
то
обе
рассмотрен
ные
параметричеСlше
задачи
являются
IшаЗllВОГНУТЫМlI.
При
построешш
р/х)
в
последней
задаче
удобнее
брать
ту
фУЮЩИЮ
/1'
которая
достигает
мю\симума
в
единствен
ной
ТОЧI{е
(см.
теорему
2.1.8),
паПРlшер,
строго нвази
вогнутую
фУШЩIIЮ
(разумеется,
если
тю\овая
среди
функ
циlr
/;
имеется).
СI\алярпзацпя
l\ШОГОI,рптерпальпых
задач
при
ПОМОЩИ
фушщпlr
вида
[~1
(f.ti/
i)81
1
/
8
1
где
s
~
1,
f.t
Е
М,
разбира
ется
в
статьях
[17,55,158].
ДЛЯ
ВОГНУТЫХ
l\ШОГОI\рптериальных
задач
согласно
теореме
2.2.2
Sj(X)
совпадает
со
множеством
решений
па
раметрическоii
задачп
вогнутого
програМШlрованпя,
состоя-
т
щей
в
мю{симпзаЦIШ
на
Х
ФУШЩИII
~
~li/i
(х)
ирп
f.t
Е
М.
i=l
Если
заменить
1\1
на
М,
то
таюш
путем
будет
выделено
множество
собственно
эффективных
решен!!ii
(теоре
ма
2.2.4).
У"азанпый
подход
берет
свое
начало
со
ста
тей
[155, 159].
п
р
II
М
е
ч
а
п
и
е
.
СI\алярпзацпеiI
называют
таЮI,е
«свертывание»
векторного
крптерия
/ =
(/"
/2'
...
, /n,)
В
одну
ЧПc.'Iовую
фУШЩIIIО
F(~t,
j)
(Ш!енуемую
обобщен
НЫМ,
агреГllровапньш
илп
глобальньш
крптерпем),
сво
дящее
исходную
многокритериальную
задачу
1\
ОДНОКРИ
териальноЙ.
n F
положительные
чпсла
~ti,
образующпе
BeI,Top
f.t,
характеризуют
относительную
вашность
нрите
риев
/1
и
называются
их
ноэффициентаllIИ
важности,
или
относительными
весами.
Если
допустить
существование
обобщенного
критерия
для
рассматриваемоiI
задачи,
то
встают
вопросы:
кю{
установпть
вид
фУЮЩИII
F
и
как
найти
величины
коэффициентов
f.tl.
На
праиине
вид
F
часто
назначается
без
наЮIх-либо
серьезных
обосноваНIIЙ
[96].
Следует,
однако,
подчеРIШУТЬ,
что
I\Ою,ретизаЦIIЯ
вида
обобщенного
I\рптерия
часто
сужает
множество
ВЫ
бора,
т.
е
дален
о
не
для
всякого
эффективного
решения
могут
существовать
таюrе
~i,
при
которых
ОНО
Мal,СИЫПЗИ
рует
F.

§ 3.5]
ПОСТРОЕНИЕ
l\IНОnШСТВА
ЭФФЕНТИВНЫХ
РЕШЕНИй
185
Для
ПРИlllера
рассмотрим
наиболее
широко
распрост
раненный
обобщенный
критерий
-
«линейную
свертку»
m
~
f1;!i.
Если
исходнан
IIIногонритериальная
задача
-
ВО-
1=1
гнутая,
то
согласно
теореме
2.2.4
любая
собственно
эффен
Тllвная
(т.
е.
по
теореме
3.1.8
<<Почти
любаш>
эффектив
ная)
оцеш{а
может
еще
быть
выделепа
I{Ю{
оптимальная.
В
противном
случае
множество
выбора
может
сильно
СОI{ратиться,
а
то
и
вовсе
оказаться
пустым.
Это
положение
иллюстрирует
следующий
пример:
n = 1,
т
=
2,
Х
=
Е,
!I(X)
=
х,
МХ)
=
е-Ж.
Здесь
Р
!
(Х)
=
Е,
т.
е
Iшждое
решенпе
является
эффентивньш.
Одна
но
накие
положительные
«веса»
f1!
и
/.12
ни
взять,
задача
максимизацпп
фУШЩlIИ
/.11Х
+
/.12ГХ
решений
пметь
не
будет,
таи
как
эта
фушщпя
не
ограничена
сверху
на
Е.
Если
же
в
I,ачестве
Х
взять,
например,
отре
З01{
[а,
Ь],
то
максимизация
указапной
фУШЩИИ
на ЭТОМ
отрезке
при
произвольных
фю{сированных
положитель
ных
/.11
и
112
будет
приводить
либо
I{
Х
=
а,
либо
к Х
=
Ь,
хотя
каждая
точка
отрезка
[а,
Ь]
эффективна.
Тююе
положение
объясняется
тем,
что
в
общем
слу
чае
каждая
эффеI{тивная
ТОЧ1{а
х
О
харю{теризуется
своим
собственным
набором
уже
не
постоянных,
а
ФУIПщиональ
ных
коэффициентов
~L!(X),
~L2(X),
•••
,
/.1т(Х),
при
ноторых
имеет место
неравенство
т
т
~
f1i
(Х)
ti
(х
О
)
>
~
f1i
(х)
fi
(х)
для
всех
Х
Е
Х
1-1
1=1
(сы.
переформулировку
эффективности
в
п.
2
из
§
2.0.
И
для
невогнутых
задач
совсем
не
обязательно,
чтобы
ЭТИ
функциональные
I\Оэффициенты
были
I\оНСТЮIтами
111'
112,
•..
,
/.1т.
Для
линейных
задач
разобранная
Сl{аляризация
при
~
Ei
М
позволяет,
I{aK
УI\азывает
лемма
2.2.4,
построить
в
ТОЧНОСТИ
множество
Pj(X)
[36,
155,
77,
149,
186].
Одна
ко
практичеСI{И
обычно
удобнее
использовать
специаль
ные
:методы,
являющиеся
прямы:lr
обобщенпем
известного
СlIмплекс-метода
линейного
программирования
[105]
на
многокритериальный
случай.
Методам
и
алгоритмам
та
Кого
рода
посвящена
уже
довольно
обширная
литература
[34,'36,
121.
142-145,
147, 151,
152,
174,
208, 210, 250,

{86
СТРУКТУРА
МНОЖЕСТВА
ЭФФЕКТИВНЫХ
РЕШЕНИЙ
[ГЛ.
3
252,
253].
Способ
построения
множества
Р
!
(Х),
основан
ный
на
решении
систем
линейных
неравенств,
определя
емых
<<ПолныМ»
набором
нонечного
числа
эффективных
точек
(т.
е.
содержащим
точку
из
каждой
гиперграни
Х,
входящей
в
Р
!
(Х»),
разбирается
в
статье
[139].
Для
двух
нритериальных
линейных
задач
удобный
способ
последо
вательных
приближений
описан
в
[134J.
ДЛЯ
отдельных
важны?С
классов
линейных
многоr,ри
териальных
задач
разработаны
специальные
методы,
представляющие
собой
развитие
методов
решения
соот
ветствующих
задач
линейного
программирования.
Напри
мер,
методы
построения
множества
эффективных
планов
переВОЗОI{
в
транспортных
многокритериальных
задачах
изложены
в
[108,
165,
177,225].
Вопросы
решения
многокритериальных
задач
квадра
тичного
программирования
разбираются
в
статьях
L2U9,
219],
а
геометрического
-
в
[205, 213].
Методы
и
алгоритмы
решения
дискретных
(точнее,
нонечных)
многокритериальных
задач,
основанные
на
идеях
(<Просеивания»
решений,
предложены
в'
работах
[18,
13,
212].
Алгоритм,
использующий
специальную
про
цедуру
построения
последовательности
решений,
описан
в
[44].
Вопросы
выделения
эффективных
решений
при
помощи
параметрической
задачи
мar{симизации
фУННЦИIl
m
~
/A-ifi
рассмотрены
в
статье
[127].
Методы
решения
мно
i=l
гокритериальных
задач
с
булевыми
переменными
изла
гаются
в
работах
[119, 120, 138, 215].
Статья
[40]
посвя·
щена
полимаТРИЧIIОЙ
задаче
коммивояжера,
а
[180]
II
[239] -
задачам
составления
раСIIисаниЙ.
В
[188]
пр
иве
дены
неноторые
оцении
сложности
задачи
выделения
ию{
симальных
точек
из
конечного
множества.
Вопросы
анализа
чувствительности
эффентивных
ре
шений
н
изменению
параметров
задачи
рассматриваются
в
работах
[152, 167, 185, 203].
Методы
регуляризации
множества
эффективных
решений
изложены
в
[35,
58]
и
[96,
гл.
8].
Методы
приближенного
построения
(аппроксимации)
)IНожества
эффективных
оценок
с
оценкой
точности
в
lJ:вухнритериальных
задачах
разработаны
в
[87, 211J.
Аппроксимация
множества
эффектпвных
точен,
состоя·
щая
в
приближенном
представлении
множества
Х
слож-

§
~.5]
ПОСТРОЕНИЕ
МНОШЕСТВА
ЭФФЕНТИВIIЫХ
РЕШЕНИЙ
187
НОЙ
структуры
конечным
числом
специальным
образом
равномерно
распределяемых
точек
и
последующим
выде
ленпем
ИЗ
них
недоминируемых,
рассматривается
D
[97J.
2.
Необходимость
проверки
эффективности
решения·
мошет
вызываться
различными
причинами.
НаПРИl\fер,
такая
проверка
необходима,
если
решение
выделено
про
цедурой,
относительно
которой
неизвестно,
приводит
ли
она
к
получению
лишь
эффективных
решений
или
может
выделять
и
не
эффеКТИВJ;lые.
Проверка
эффективности
ре
шений
может
ОСУЩЕСТВЛЯТЬСЯ
и
при
с!{аляризации,
осно
ванной
на
необходимых,
но не
достаТО'IIIЫХ
УСЛОВИЯХ
эф
феI{ТИВНОСТИ.
Нередко
ВОЗНИI,ает
необходимость
проверни
эффектив
ности
решения,
которое
уже
было выбрано
(назначено)
ПО
каким-либо
соображениям
или
даже
ранее
использо
валось.
При
этом
целью
проверIШ
является
выяснение
ПРПНЦllпиальной
возможности
улучшения
рассматривае
мого
решения
н,
если
такая
возможность
имеется,-
полу
чения
эффективного
решения,
более
предпочтительного,
че~1
исходное.
Для
проверки
эффеl\ТИRНОСТИ
решения
можно
исполь
зовать
подходящие
условия
оптимальности,
изложенные
во
второй
главе.
I\aK
обычно,
если
дл~
проверки
исполь
зуются
необходимые
условия
и
оказывается, что
рассмат
рнваемое
решение
им
удовлетворяет,
то
гарантировать
его
эффективность
нельзя.
ОДНaI{О
если
эти
условия
не
вы
полняются,
то
решение
не
эффентивно.
Если
для
провер
ки
используются
достаточные
условия,
то
решение,
удов
летворяющее
ИМ,
эффентнвно.
Если
же
такие
условия
не
выполняются,
то
вопрос
об
эффеI{ТИВНОСТИ
решення
оста
ется
открытым.
НaIЮНОЦ,
если
при
меняются
необходимые
Il
достаточные
условия,
то
проверяемое
решение
эффеI,
тивно
в
ТОМ
И
толыю
том
случае,
I{огда
оно
этим
УСЛОВИЯllI
удовлетворяет.
Среди
всех
условий
главы
II
специально
отметим
лишь
условия,
сформулировапные
в
при
мере
2.1.7.
Эти
условия
эффективности
ЯВЛЯЮтся
необходимыми
и
доста
точными.
Следовательно,
проверяеz,юе
решение
х
О
эффек
тивно
тогда
и
только
тогда.
когда
оно
маКСИllIизирует
функцию
т
~
fi
(х)
(1)
(=1

188
СТРУНТУГЛ
1I1I!ОJIiССТВЛ
ЭФФIШТИВПЫХ
РЕШEIШЙ
[ГЛ.
3
на
множестве
{х
Е
Xlft(x) G;
/i(XO),
i =
1,
2,
...
,
т}.
(2)
Весьма
ценно
то,
что
в
случае,
когда
решение
х'
не
эф
фективно,
максимизация
функции
(1)
на
множестве
(2)
приводит
к
получению
эффеI\Т/IВНОГО
решения
х*,
I\ОТО
рое
более
предпочтительно,
чем
х
О
,
т. е.
l<х*);:;:::
/(хО)
(CM~
[77,241]).
Подчеркнем,
что
если
исходпая
МНОГОl\ритери
альная
задача
вогнута
(линейна),
то
вадача
маКСИl\Iиза
ции
(1)
на
множестве
(2)
оказывается
вадачеЙ
вогнутого
(сответственно
линейного)
программированил.

ГJIЛВЛ
4
ДВОЙСТВЕННЫЕ
МНОГОНРИТЕРИАЛЬНЫЕ
ЗАДАЧИ
Вопросы
двойственности
для
МНОГОI<ритериальных
за
дач
значительно
сложнее
аналогичных
вопросов
для
за
дач
с
одним
критерием.
Дело
в
том,
что
понятие
двойст
венности
в
МНОГОI\ритериальной
оптимизации
основщIO
на
соотношении
маI\симальных
и
минимальных
элементов
в
частично
упорядоченных
множествах,
в
отличие
от
двоп
ственности
в
обычной
теории
оптимизации
[241,
где
двой
ственность
связана
с
совпадением
маl\симальных
и
мини
мальных
элементов
линейно
упорядоченных
множеств
на
вещественной
прямой.
Этот
переход
от
линейно
упорядо
ченных множеств
на
прямой
к
множестваl\l
в
еnклидовом
пространстве
при
изучении
двойственности
Оll:азывается
нетривиальны},{.
Грубо
говоря,
в
CI\аЛЯРНОl\l
случае
для
получения
совпадения
решений
прямой
и
двойственной
задач
достаточно
убедиться
в
отсутствии
«разрыва»
101еж
ду
множествами
образов
решений
прямой
и
двойственноii
задач.
Если
такого
«разрыва»
нет,
то
уназанные
множе
ства
образов
«склеиваются»
в
ТОЧ1\е,
которая
дает
одно
временно
решение
прямой
и
двойственной
задач.
В
IIIНО
гокритериальном
случае
этого
«склеивания})
прямого
1\
двойственного
множеств
недостаточно;
двойственная
кон
СТРУIЩИЯ
должна
быть
такой,
чтобы
прямое
и
двойствен
ное
множества
«склеивалисы)
в
точности
своими
множе
ствами
!lIaксимальных
и
минимальных
элементов.
Имеющиеся
публикации,
посвященные
двойственности
в
МНОГОIl:ритериальной
оптимизации,
условно
можно
pa1l-
бить
на
две
группы.
В
первой
группе
работ
[67, 154, 173,
175,
176,
185,
2'14,
218, 232]
двойственность
тан
или
ИН(1-
че
связана
с
определенного
типа
функциями
Лагранжа.
Во
второй грунпе
работ
[164, 234, 254]
двойственность
Изучается
с
ИСПОЛЬЗ0ваннем
аппарата
сопряженных
функ
ций
и
имеющиеся
здесь
результаты
представляют
собой
дальнейшее
обобщение
теории
двойственности
Фенхеля.
Не
касаясь
работ
второго
направления,
в
данной
главе

190
двоnr;ТВЕIIНЫЕ
МНОГОНРИТЕРИАЛЬНЫЕ
ЗАДАЧИ
[ГЛ.
~
па
основе
результатов
авторов
[67,
84.]
предлагается
такая
I\ОНСТРУКЦИЯ
двойственности,
D
ра:lШИ
l{оТОРОЙ
в
той
или
иной
степени
Уlшадываютсл
подходы
первой
группы
работ.
В
первом
параграфе
Этой
главы
рассматриваются
общетеоретические
вопросы
о
седловых
ТОЧI\аХ,
l'.IаI\СИl\Ш·
пах и
минимаксах
векторных
фУШЩИЙ.
Во
втором
параг·
рафе
вводится
общая
конструкция
двойственных
много·
I\ритерпальпых
задач.
Третий
и
четвертый
параграфы
по·
священы
вопросам
двойствеНПОСТII
соответственпо
для
вогнутых
и
линейных
многокритериальных
задач.
§ 4.1.
Седло
вые
пары,
максимины
и
мипимаксы
векторных
функций
RлассичеСI\ая
теория
двойственности
в
матемаТ'иче·
ском
программировании
широко
использует
понятия
ceд~
ловой
пары,
маl\симина
и
минимакса
числовой
функции.
В
этом
параграфе
аналогичные
понятия,
необходимые
для
развития
теории
двойственности
многокритериальной:
оптимизации,
вводятся
для
векторных
функций.
1.
Пусть
векторная
функция
к(х,
у)
= (Kt(x,
у),
Kz(x,
у),
• '"
Кт(х,
у»
определена
на
декартовом
ПроН3-
ведении
Х
Х
У
(здесь
и
далее
в
этом
параграфе
непустые
}шожества
Х
и
У
могут
иметь
произвольную
природу
).
Вектор
(х
о
,
уО)
Е Х Х
У
будем
называть:
СUДЫlОЙ
сед.лО80Й
парой,
если
К(х,
уО)
~
К(х
О
,
уО)
s
К(х
О
,
у)
для
всех
х
е
Х,
у
Е
У;
,(1)
СUДЬ1l0-сдабой
седдовой
парой,
если
к(х,
YO~
<К(х
О
,
уО)
:::;,
К(х
О
,
у)
для
всех
х
Е
Х,
У
Е
У;
(2)
сдаБО-СUДЬ1l0Й
седдовой
парой,
если
к(х
,
уО)
~
К(х
О
,
уО)
<.
К(х
О
,
11)
для
всех
х
е Х
4
у
Е
У;
,(3)
сдабой седловой
парой,
если
К(х,
уО)
<К(х
О
,
уО)
<
К(х
О
,
у)
для
всех
х
Е
Х, У
е
У.
(4)
