Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач

Подождите немного. Документ загружается.

§ 4.1]

СЕДЛОВЫЕ

ПАРЫ,

МАНСИМИНЫ

И

МИНИМАНСЫ

191

Согласно

определению

отношений

>

и

::>

(§

1.2)

вы

полнение

соотношения

К(х,

уО)

<

К(хО,

уО)

при

всех

х

е

Х

означает,

что

соотношение

К(хО,

уО);;::;

К(х,

уО)

не

выполняется

ни ПрИ

каком

х

Е

Х.

Аналогично

выполне

ние

соотношения

К(хО,

уО)

<К(х

О

,

у)

при

всех

у

Е

У

означает,

что

соотношение

К(х

О

,

уО)

2

К(х

О

,

у)

не

выпол

няется

ни

при

каком

у

Е

У.

Понятно,

что

всякая

сильная

седловая

пара

является

седловой

в

CMblCJle

(2)-(4),

а

всякая

полусильная

(силь

но-слабая'

или

слабо-сильная)

седловая

пара

является

также

и

слабой.

Сильная

седловая

пара

-

это

обычная

седловая

точка

одновременно

всех

компонент

вектор

функции

К:

(1)

справедливо

тогда

и

только

тогда,

когда

при

каждом

i =

1,

2,

...

,

т

выполняются

неравенства

к;(х,

уО)::;;

к,(хО,

уО)

~

IC(xo,

у)

для

всех

х

Е

Х,

У

Е

У.

В

связи

с

этим

ясно,

что

существуют

сильные

седловые

пары

довольно

реДI{О.

Введем

в

рассмотрение

следующие

четыре

множества:

Ql=

U n

!gEEтlg<K(x,y»)~

ХЕХуЕУ

Q2=

U n

(gEEт\g>K(x,y»),;

I/EY

ХЕХ

Н

1 = U n

(h

Е

Е

т

I h <

К

(х,

у»)

~

ХЕХ

I/EY

Н2=

U n

!h,EEтlh>K(x

1

у»).

уЕУ

ХЕХ

Эти

множества

имеют

естественную

интерпретацию

в

теоретико-игровых

терминах,

если

К

означает

векторную

функцию

выигрыша,

а

Х

и

У

-

множества

стратегий

первого

и

второго

игроков

соответственно

(первый

игрок

стремится

«максимизироватЬ»

функцию

выигрыша).

В

этом случае

QI

-

это

множество

выигрышей,

которые

может

себе

гарантировать

первый

игрок

(короче,

его

га

рантированные

выигрыши),

а

НI

-

множество

выигрышей,

",оторые

он

может

не

позволить

ухудшить

второму

игро·

НУ

«(защищаемые»

выигрыши).

Аналогичный

смысл

имеют

множества

Q2

и

Н2

дЛЯ

второго

игрока.

Непосредственно

ШJ

определений

введенных

множеств

легко

получить

включения

QI

slJl,

Q2

s lf2,

которые

та[,

же

имеют ясный

теореТИItо-игровой

смысл.

{92

ДВОЙСТВЕННЫЕ

l\ШОГОl\РИТЕРИАЛЬНЫЕ

ЗАДАЧИ

[гл.

&

Т

е

о

р

е

м

а

1.

Справедлuвы

СООТ1tOlUе1111Я

ql

~

q2

для

всех

ql

Е

Q\

q2

Е

Q2;

(5)

q <.Jl

для

всех

q

Е

Qt,

h

Е

НЗ;

(6)

h

<.q

для

всех

hEH',

qEQ3.

(7):

Д

о

I(

а

з

а т

е

л

ь

с

т в

о.

Из

определений

множеств

Ql

и

Q2

имеем

q!

Е

QI

+->-

q!

::::

к

(х

О

,

у)

для

неIЮТОРОГО

х

О

Е

Х.

И

любого

у

Е

У;

(8)

q2

Е

Q2

+->- К

(х,

уО)

<

q2

для

неIЮТОРОГО

уО

Е

У

и

любого

х

Е

х.

(9);

Отсюда

q!

;;а

К(х

О

,

уО)

~

q2.

Для

доказательства

(6)

предположим

противное:

q:>

h

и

q

Е

Q"

h

Е

Н

2

•

Это

означает,

что

при

некоторых

х

О

Е

Х,

у"

Е

У

справеДЛIIВО

К(х

О

,

у)

~ q

>h>

К(х,

уn)

для

всех

х

Е

Х,

У

Е

У.

При

х

=

х

О

,

у

=

уО

отсюда

BblTeI{aeT

противоречие.:

К(х

О

,

уО)

=1=

К(х

О

,

уО).

Соотношение

(7)

ДOIшзывается

аналогично

.•

Теорема

1

ПОIщзывает,

что

аllалого,м,

,м,акси,м,и1lа

(,м,и

пи,м,акса)

является

пара

МИОЖеств

QI

и

Н'

(соответствен

но

Q2

и

Н

2

),

а

неравенству

(т

=

1)

тах

min

К

(х,

у)

<.

min

шах

К

(х,

у)

хеХ

lJеУ

lJеУ

хеХ

соответствуют

свойства

этих

множеств

(5)-(7).

2.

Простейmие

примеры

показывают,

что

пары

(х',

у')

н

(х",

у"),

седловые

в

смысле

(2),

(3)

или

(4),

могут

быть

несравнимыми

(т. е.

не

верно

ни

К(х',

у')

~K(x",

у"),

ни

К(х',

у'):5:

К(х",

у"»

llЛИ

доминировать

одна

над

другой

(например,

К(х',

у')

;;;:::'К(х",

у"».

А

пары

(х',

у")

и

(х",

у')

могут

не

быть

седловыми.

Однако,

согласно

нижеСJlедующему

утверждению

существование

сильной

седловой

пары

нarшадываетсущественные

огра

ничения

на

CTPYI,TYPy

множеств

полусильных

седло

вых

пар.

Пусть

W"

(соответственно

fV''',

TVw"

WWW)

-

множест

во

сильных

(соответственно

остальных

трех

типов)

сед·

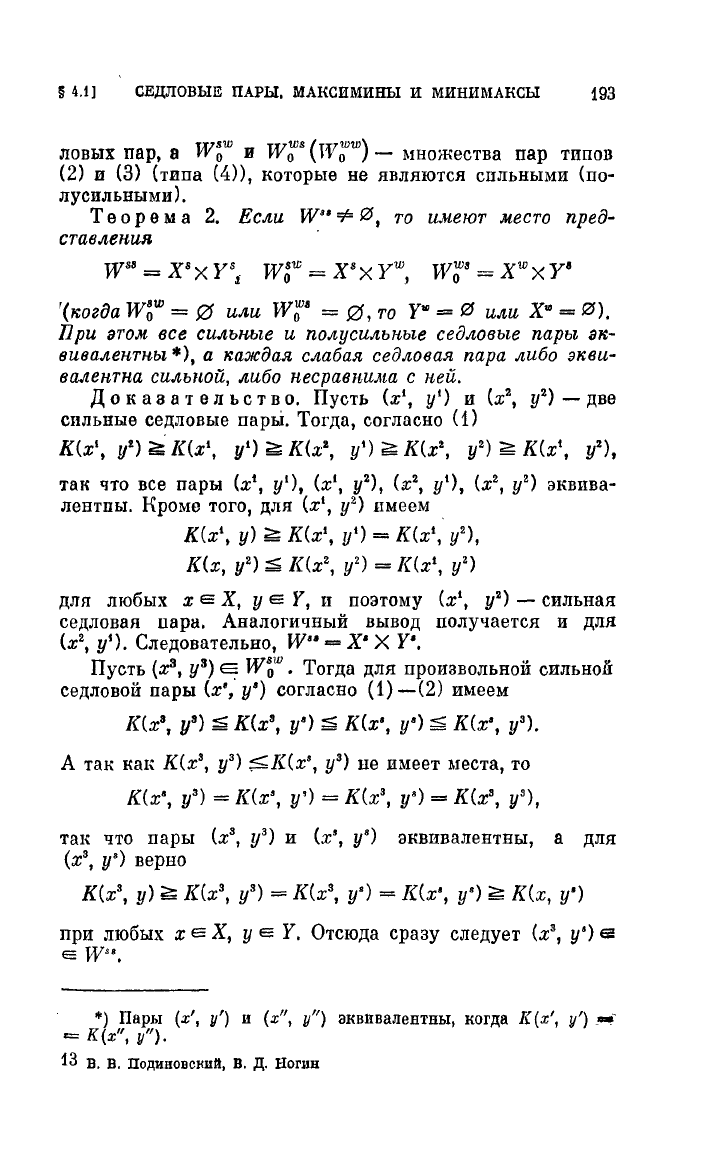
§ 4.1)

СЕДЛОВЫЕ

ПАРЫ,

МАКСИМИНЫ

И

МИНИМАКСЫ

193

ловых

пар,

а

w~w

и

W~8

(JV~W)

-

множества

пар

типов

(2)

и

(3)

(типа

(4»,

которые

не

являются

сильными

(по

лусильными)

.

Т

е

о

р

е

м

а

2,

Если

W'·.:F

0,

то

имеют

место

nред-

ставлеnия

.

W

88

=

Х

8

Х

Y

S

t

wgw

=

Х

8

Х

у

ш

,

Т-V~8

= X

W

ХУа

r(~ozBa

w~w

= 0

или

W~8

=

0,

то

У'"

= 0

или

Хш

=

0),

При

этом

все

сильnые

и

nолусильnые

седловые

пары

Э~

вивалеnТnЬJ*),

а

~а~дая

слабая

седловая

пара либо

эквu

ва.леитnа

сиЛЫlОЙ,

лuбо

necpaenUltta

с

ией.

Доказательство.

Пусть

(х"

у')

И

(х

2

,

у2)

-две

сильные

седловые

пары.

Тогда,

согласно

(1)

K(xt,

у2)

s:

[(х"

у')

~K(xZ,

yt)

~

K(xZ,

у2)

~

K(xt,

у2),

так

что

все

пары

(xt,

у'),

(x

l

,

у2),

(х

2

,

yl),

(х

З

,

уЗ)

эквива

лентпы.

Кроме

того,

для

(х"

у2)

имеем

К(х"

у)

~

К(х

'

,

yl)

=

К(х

'

,

уЗ),

К(х,

уЗ)

~

[(х\

у2)

=

{((х',

у2)

ДЛЯ

любых

х

е

Х,

у

е

У,

и

поэтому

(х"

у2)

-

сильная

седловая

паРI:l,

Аналогичный

вывод

получается

и

для

(х

З

,

у').

Следовательно,

W"

=

Х'

Х

У',

Пусть

(Т,

уЗ)

~

w~w

,

Тогда

для произвольной

сильной

седловой

пары

(х',

у')

согласно

(1)

-(2)

имеем

[(х

8

,

уЗ)

~

К(х

З

,

у')

~

К(х',

у')

-<

К(х',

уЗ),

А

та1\

кю,

К(х\

уЗ)

-;::::.К(х·,

уЗ)

не

имеет

места,

то

К(х',

уЗ)

=

J((х',

у')

=

К(х

З

,

у')

=

К(х\

уЗ),

тю,

что

пары

(х

З

,

уЗ)

и

(х',

у')

эквивалентны,

а

для

(х

З

,

у')

верно

К(х

З

,

y)~

к(хз,

уЗ)

=

К(х

З

,

у8)

=

[(х',

у8)

~

[(х,

у')

при

любых

х

Е

Х,

У

Е

У,

Отсюда

сразу

следует

(х

3

,

у')

Eii!

е

W

sв

,

*)

Пары

(х',

у')

и

(х",

у")

Э}ШlIвалевтвы,

когда

[(

(х',

у')

.-"

=

К(х",

у").

13

в. Б.

ПОДИНОВСRПЙ,

в.

Д.

Ногин

194

ДВОйСТВЕННЫЕ

многонритЕриАльныE

ЗАДАЧИ

[ГЛ.

,

Для

(х',

уЗ)

при

любых

х

Е

Х, У

Е

У

имеем

лишь

К(х',

у)

~

К(х',

у')

=

К(х',

уЗ)

>-

К(х,

уЗ),

причем

если

для

неноторого

х'

пары

(х',

у')

и

(ха,

уа)

бы

ли

несравнимы

(а

таRОЙ

I)лемепт

х'

по

условию

найдется),

то

и

(х',

уЗ)

и

(х',

уЗ)

очевидно,

таRже

несравнимы.

По

этому

(х'

~

уЗ)

е

W~w.

Предположим,

что

и

(х',

у4)

Е

wgw.

Согласно

(1),

(2)

к(х

з

,

y~)

~

К(х

l

,

уЗ)

=

К(х',

у')

~

к(х\

у')

~

К(х"

y~).

А

тан

нан

в

соответствии

с

(2)

К(х

3

,

yi)

-<

К(х\

yi),

то

пары

(ха,

у'),

(х\

уЗ)

и

(х"

у")

эквивалентны.

Поэтому

для

любых

х

Е

Х,

У

Е

У

можно

записать

к(хз,

у)

~

К(х

З

,

уЗ)

=

К(х\

y~)

>-К(х,

у"),

причем

если

пары

(х",

y~)

и

(х"

y~)

были

несравнимы

(такой

элемент

х"

по

условию

существует),

то

и

(х",

у")

и

(х

3

,

у')

также

несравнимы.

Поэтому

(х

3

,

у4)

eW~w.

Ана

логично

проверяется

(х

4

,

уЗ)

Е

w~w.

Следовательно,

W~w

=

=

X'xyw.

Равенство

w:'

=

XWx

У'

получается

из

дока

занного

равенства

для

W~w

заменой

х

на

у,

а

у

на

х.

Наконец,

если

(х

б

,

уБ)

Е

W~w,

то

предположение

К(х\

y~)

~K(x',

у')

приводит

согласно

(1)

к

K(x~,

y~)

~,

~

К(х\

у'),

а

предположение

К(х',

у');:;;;:

К(х

5

,

y~)

-

К

К(х',

у5)

"2:.

К(х\

y~).

Любое

из

этих

неравенств

противо

речит

(4)

••

3.

Взаимосвязь

между

значениями

вектор-функции

К

на

седловых

парах

и

множествами

QI,

Q2,

Н

1

И

Н2

уста

навливает

т

е

о

р

е

м

а

3.

Справедливо

в.,.лючеnие

и

равеnства

K(W")

=

QI

n

Q2,

K(WWW)

s;

НI

n

Н2

(10)

K(W

W

')

=

НI

n

Q2,

(11)

причем

а) вся.,.иЙ

элемеnт

z"

Е

К(

W")

является

nаибольши,м

во

мnоже~тве

QI,

ма1>симальnым

во

мnожестве

H

1

,

nаи

меnьшим

в

Q2

и

миnимальnым

(J

H

2

j

§

4.11

CEДJIOBЫE

ПАРЫ,

МА1{сttМttны

и

МИНИМА1{СЫ

{95

б)

вся~ий

вле.мен,т

z"·

Е

К(

W·

..

)

является

.ма~сuмаль·

н,Ы.ilt

в

Q!

и

.iltин,шtальн,ы.ilt

в

Н

2

;

.

в)

вся~uй

э.ле.iltен,т

z"·

Е

K(WIO')

является

.мин,и.iltальн,ы,м

в

QZ

и

.ма~си.мальн,ы.м

в

Н

'

.

--.заметим,

что

утверждения

а)

-

в)

теоремы

почти

це

ликом

вытекают

из

результатов

работы

[92].

Д

о

к

а

з

а т е

л

ь

с т

в

о.

Опираясь

непосредственно

на

определения

(1)-(4),

можно

Л~ГRО

установить

ВRлючения

K(WIO

..

)

,=НI

n

Н

2

,

КCW")

'=

QI

n

QZ,

K(W''')

'=

QI

n

НЗ,

K(W"')

'=

QZ

n

н'.

Например,

если

z8t·

=

К(х',

уш),

то

согласно

первому

неравенству

(2)

z'"

~

К(х',

у)

для

всех

у

е

У,

и

поэтому

z'"

Е

QI.

Аналогично,

из

второго

соотношения

(2)

следует

z·

..

::>

К(х,

yVl)

для

всех

х

Е

Х,

что влечет

Z'Vl

Е

Н2.

ДОRажем

требуемые

обратные

включения.

Пусть

q*

Е

QI

n

QZ.

При

у

=

уО

И Х

=

х

О

из

(8)-(9)

для

qO

"'"

=

К(х

О

,

уО)

получаем

qO

~

q*

~

qO,

тан

что

qO"",

q*.

Поэто~

ыу

из

(8),

(9)

сразу

следует,

что

(х

О

,

уО)

-

сильная-

седло~

вая

пара.

Таким

образом,

K(W")

;;;;i!

QI

n

Q2.

Далее,

_для

q*

Е

QI

Л

Q2,

ql

Е

QI,

q2

Е

Q2,

h

l

е

Н!,

h

3

Е

НЗ

по теореме

1

имеем

q*

~

q"

q*:a

qZ,

q*~

h

'

,

q*

<h

2

.

Поэтому

элемент

q*

является

наибольшим

в

MHO~

жестве

QI,

наименьшим

в

QZ,

максимальным

в

Н'

И

мини

мальным

в

нз.

Утверждение

а)

доказано.

Теперь

пусть

z*

Е

Q!

n

Н'.

ДЛЯ

у

-=

уО

их

....

х

О

из

(8)

и

h

Е

на

++

h

5

К

(Х,

уО),

при

нен.отором

уО

е

f

и

каждом

xsX

получаем

К(х

О

,

уО)

ie:

z*

5

К(х

О

,

уО),

так

что

К(х',

уО)

....

==

Z*.

Поэтому

(х

О

,

уО)

ei W

..

••

Таким

образом,

K(W'Vl);;;;!

0:2

QI

n

HZ,

и,

учитывая

полученное

ранее

обратное

вилю

чеuие,

приходи?'!

к

равенству

K(W"')

-

QI

n

н·.

Далее,

для

z*

Ei

QI

n

на,

q 6J

QI,

h

ЕВ

НI

согласно

теореме

1

имеем

z*

~

q

и

z*

~

h.

Утверждение

б)

доказано.

Для

слабо-сильной

седловой

пары

ДОН8вательство

aHa~

логично

приведеННQМУ

выше.

• .

Обозва1JИМ через

MaxQI

(MinHZ)

множество

манси~

мальныХ

(МИВИ1.JaЛЬНЬХХ)

по::::

элементов

множества

13"

196

ДВОЙСТВЕННЫЕ

многоI\рIIтЕриАлыlыE

ЗАДАЧИ

[ГЛ.,

Q!

(Н

2

),

Поскольку

Мах

Q!

n

Min

Н

2

>=

Q!

n

Н2,

а

по

утверждению

б)

из

теоремы

3

К(

W81D)

>=

Мах

QI n

Min

IР,

то

с

учетом

(11)

можно

записать

K(W'U»

=

Мах

Q!

n

Min

Н

2

,

(12)

Аналогичные

равенства

справедливы

таЮRе

дЛЯ

KO'VU>8)

и

K(WSS).

Рассмотрим

несRолыо

примеров,

иллюстрирующих

до

казанные

теоремы.

Во

всех

этих

примерах

Х

=

у

= {1,

2},

а

значения

beRTOP-ФУЮЩllИ

к(х,

у)

=

(к,(х,

у),

к

2

(х,

у»

задаются

матрпцей,

причем

х

-

номер

ее

строки,

у

-

но

мер

столбца.

Х2

~

lr2

.]

;;

~

2

~

2

!/'

~

1

~a7$P~~1!

! -

О

1ft?).

W~

~.j'И/'

о/ш1:"'

о

'~

г

J

I!f

~

н

2

Рис.

1,

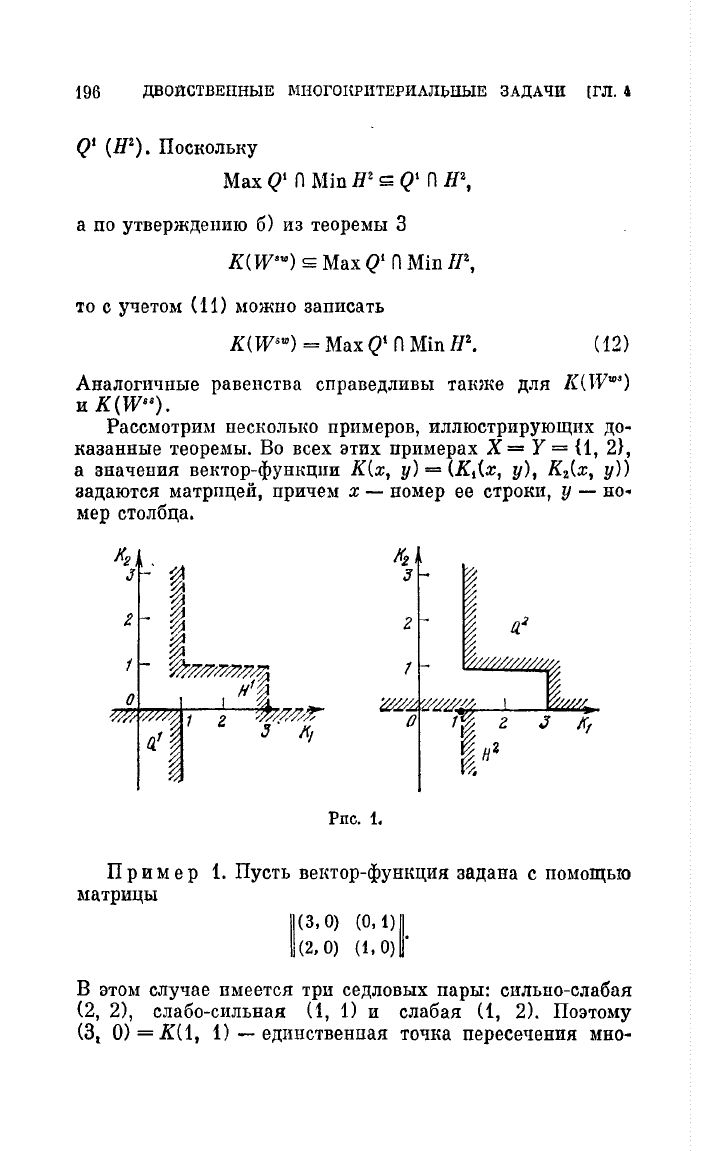
При

м

е

р

1.

Пусть

beI\TOP-фУНRЦИЯ

задана

с

помощью

матрицы

11

(З,0)

(0,1)//,

(2,0)

(1,0)~

В

этом

случае

имеется

три

седловых

пары:

сильно-слабая

(2,

2),

слабо-сильная

(1,

1)

и

слабая

(1,

2).

Поэтому

(31

О)

=

К(1,

1)

-

единственпая

ТОЧRа

пересечения

мно-

§

Н)

СЕДЛОDЫЕ

ПАРЫ,

мАRсI!мины1

n

МИНИМАRСЫ

{97

жеств

Q2

U

пt,

а

(1,

О)

=

[«2,

2)

-

единственная

точка

пересечения

множеств

QI

и

Н2

(см.

рис.

1).

Заметим,

что

здесь

(2,

О)

е

н·

n

на,

таl\

что

ВRлючение

(10)

оказывает

ся

строгим.

При

м

е

р

2.

ФУНIщия

К,

заданная

с

помощью

мат

рицы

11

(2.2) (2.3)

11

~(1,1)

(3,O)W

пмеет

две

седловые

пары:

силь-

ную

(1,

1)

И

слабую

(2, 2).

Мно

жества

QI

И

Q2

имеют

единствен

ную

общую

точку

(2,

2)

=

К(

1,

1)

(см.

рис.

2).

ПРИ

М

е

Р

3.

ФУНI\ЦИЯ

К,

за

данная

матрицей

/1

(О,

2)

(1,

О)

11'

(О,

1) (2.

О)

,

,

...

Q

q'

I

2

.1

·лt

-

Рис.

2.

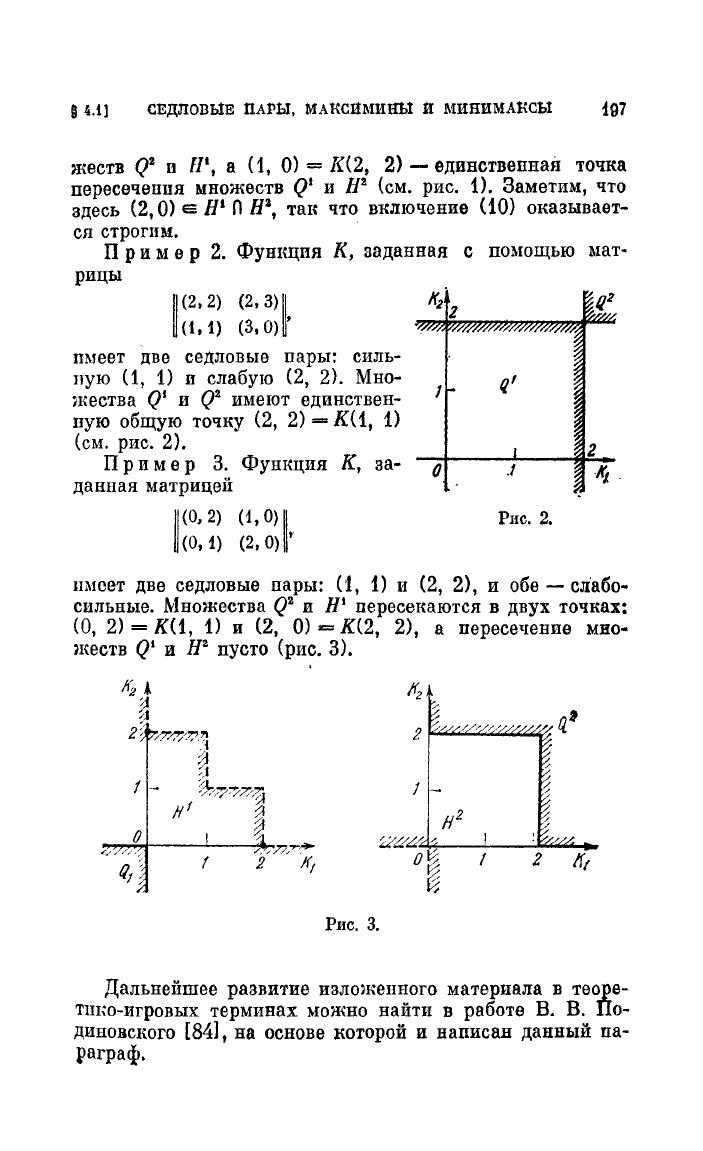
имеет

две

седловые

пары:

(1,

1)

и

(2, 2),

И

обе

-

слабо

сильные.

.множества

Q2

и Н'

нересеI\аЮТСЯ

в

двух

точках:

(О,

2)

=

К(1,

1)

и

(2,

О)

=

К(2,

2),

а

пересечение

мно

шеств

QI

и

Н

2

нусто

(рис.

3>.

,

I -

2 /({

Рис.

3.

Дальнейшее

развитие

изложенного

материала

в

теоре

ТIШО-ИГРОВЫХ

терминах

можно

найти

в

работе

В.

В.

По

Диновского

[84] I

на

основе

RОТОРОЙ

и

написан

данный

па

раграф.

{98

ДВОЙСТВЕННЫЕ

мпогоRритЕриАлыIыE

ЗАnАЧИ

[ГЛ.

~

§ 4.2.

Общая

конструкция

двоiс'rвениых

задач

в

этом

параграфе

ВВОДИТСЯ

векторная

функция

Лаг·

ранжа

и

показывается,

что

задача

отыскания

эффективных

решений

в

исходной

многокритериалъной

задаче

TeCHQ

связана

с

задачей

отыс!,ания

седловых

пар

функции

Лаг.

ранжа.

Формулируется

пара

двойственных

задач,

которые

зaJtлючаются

в

нахождении

максимальных

элементов

прямого

множества

и

минимальных

элементов

двойствен

ного

множества

Соответственно.

Устанавливается,

что

множество

решений,

являющихся

одновременно

решения

ми

прямой

и

двойственной

задач,

представляет

собой

пе

ресеч:ение

прямого

и

двойственного

множеств

псовпадает

с

множеством

значений

функции

Лагранжа

на

совокуп~

ноств

ее

седловых

пар.

.

1 ..

Пусть,

как

и

в

предыдущих

главах,

вектор-функции

1 -

(lf'

1а,

...

,

1т)

и

g = (gf'

g2,

••.

,

g,,)

заданы

на

множе·

стве

D

si

Е",

а

(1)

Введем

ве1>ТОРnУЮ

фующuю

Лаграnжа

Цх,

1..)

=

(!t(x)

+

(Л,

g(x»,

мх)

+

(л.,

g(x»,

•••

"',

Im(x) +

(Л,

g(x»)

(2)

и

рассмотрим

свойства

различного

типа

седловых пар

этой

функции

на

множестве

D

х

E~.

Т

е

о

р

е

м

а

1.

Д,м

фующии

Лаераnжа

(2)

nоnятuя

еидьnой

и

слабо-еильnой,

а та-кже

еильnо-елабой

и

ела-

БQй

седА.Овых

пар

па

D

Х

Е.,?

э",вивадеnтnы:

W"

= W''', W'" =

W.....

(3)

Есди

(х

о

,

1..0)

-

еедловая

пара

L

Jtюбого

типа,

то

g(XO)

~

0(1),

(1..0,

g(XO»

=

О,

(4)

тап

что

х

О

Е

Х.

При

этом

еСАи

(хО,

1..0)

Е

W"1D,

ТО

хО

-

эф

феnти8nОВ

решеlще

(т.

е.

х

О

Е

Ft(X»,

а

если

(хО,

1..0)

Ei

W",

1'0

хО

-

rочnа

MancUМYMa

па

Х

nаждой

из

фующий

If'

Is,

...

,

1m.

Доказательство.

Для

седловой

пары

(х

о

1

л.

О

)Е

Е

D

Х

E~

ПРОИЗ1ЮЛЬНОГО

типа

всегда

выполняетс~

L

(х

О

!

1..0)

< L

(х

О

!

л)

для

всех

л

Е

E~.

(5)

-

§ 4.2)

ОБЩАЯ

lЮНСТРУIЩИЯ

ДВОйСТВЕННЫХ

ЗАдАЧ

199

Отсюда

учитывая

(2)

получаем

(4)

п

в

силу

(1)

х

О

е

Х.

Далее,

если

верно

(4),

то,

очевидно,

верно

и

L

(х

О

,

л

О

)

:5

L

(xo

J

л)

для

всех

л

Е

E~.

(6)

Наконец,

при

выполнении

(6)

справедливо

и

(5).

Следова·

тельно,

для

седловой

пары

(ХО,

лО)

произвольного

типа

условия

(4), (5)

и

(6)

эквивалентны.

Отсюда

следуют,

в

частности,

равенства

(3).

Для

(хО,

лО)

е

WfD

..

выполнено

L(xO,

л

О

)

;>L(x,

л

О

)

для

всех

х

е

D.

Согласно

(4)

отсюда

следует,

что

!(хО);>

!(х)

для

всех

х

е

Х,

т.

е.

х'

-

эффентивное

решение.

Наконец,

если

(ХО,

лО)

е

W",

то

L(x',

лО)

~

ЦХ,

).0)

для

всех

х

е

D,

откуда

в

силу

(4)

/lCxO)

~

!,

(х)

для

каждого

i

е

М

и

всех

хеХ

.•

Теорема

1

показывает,

что

слабые

седловые

пары

функции

L

прямым

образом

связаны

с

эффективными

решениями

исходной

МНОГОI{ритериальной

задачи.

В

даль·

нейшем

будем

рассматривать

лишь

слабые

седловые

па·

ры

L

и,

ради

краткости,

будем

просто

называть

их

сед·

лов~ми

парами,

8

множество

всех

таких

пар

будем

обо·

значать

через

W.

2.

Введем

множества

Q =

QI

И

Н

=

Н2

(§

4.1),

кото

рые

будем

называть

прямым

и

двойственным

соответст

венно:

Q = U Q(x),;

::cED

Q

(х)

= n

{q

Е

Е

т

I q

~

L

(х!

л)}1

k

"'ЕЕ>

=

Н(л)=

n

(hЕЕтlh;>L(хJЛ)}.

::CED

Нетрудно

проверить,

что

если

х

е

D\X,

то

Q(x) =

о,

поэтому

Q=

U

Q(x)=

U

{qEEт\q<!(x)]=Y*,

(7)

::сЕ.!:

ЖЕ.!:

-

где,

I{aK

и

ранее,

У",

=

У

-

ЕТ;.

.

""

200

ДВОйСТВЕННЫЕ

МНОГОНРИТЕРИАЛЬНЫЕ

ЗАДАЧИ

[ГЛ,

~

Заметим

также,

что

согласно

лемме

1.2.1

МНОЖество

Н(л)

можно

представить

и

в

таком

виде:

Н

(л)

= n U {h I

<11,

h)

> 2

(11,

Х

I

л)}t

(8)

XED

IlEM

rдe

2 -

скалярная

ФУНlщия

Лагранжа:

2(f1,

х,

л)

=

<f1,

L(x,

л».

Множество

максимальных

(минимальных)

по

>

эле~

ментов

множества

Q

(множества

Н)

будем

обозначать

че~

рез

Мах

Q (Min

Н).

Теорема

1.3

и

ра)3е.нство

(1.12)

пока~

Щ>Iвают,

что

множество

значений

функции

Лагранжа

L

на

?tlВожестве

сеДЛовых

пар

W

тесно

связано

с

множе~

ствами

Мах

Q

и

Min

Н.

Т

е о

р

е

м

а

2.

Справедливы

равенства

Мах

Q n

MinH

= Q n

н

=

L(fЛ.

(9)

Согласно

этой

теореме,

если

Мах

Q

s;

Min

Н*),

то

MaxQ=QnH=L(W);

если

Мах

Q;;;:)

Min

Н,

то

МiпП'

Q n

I/

=

L(W);

наконец,

если

Мах

Q = Min

Н,

то

MaxQ =

MinH

= Q n

н

=L(fV,

(10)

3.

Благодаря

(7)

и

лемме

2.2.1

имеют

М,есто

равен-

ства

l\IaxQ=l\Iax

U

Q(x)=MaxY"'=P(Y)t

(11)

ХЕХ

где,

нак

и

раньше,

Р(

У)

-

множество

эффеI<ТИВНЫХ

оце

нок исходной

многокритериальной

задачи.

Итак,

следующие

две

задачи

являются

эквива~

леНТНЫАШ:

Пр

я

м

а

я

(1

а

Д

а

ч а

1.

Найти

1IIножество

Мах

Q.

Пр

я

м

а

я

з

а

Д

а ч

а

2.

Найти

множество

Р(

У).

*)

ЗаllIеТИIlI,

что

в

сналярном

случае

строгие

включения

Мах

Q

с:

Min

Н

(Мах

Q

~

Min

Н)

смысла

не

имеют,

тан

нан

при

т

= 1

неравенство

шах

Q n

шiп

Н

'#

f25

влечет

равенство

шах

Q =

"'"

minH. .