Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач
Подождите немного. Документ загружается.


ГЛАВА
3
СТРУКТУРА
И
СВОЙСТВА
МНОЖЕСТВА
ЭФФЕКТИВНЫХ
РЕШЕНИН
в
этой
главе
формулируются
УСЛОВIШ
существова~
пия
эффективuых
точен,
достаточные
условия
замкнуто~
сти,
дугообразноii
связности
и
стпгиваемости
в
себе
MHO~
жества
эффективных
точек,
устанавливается
тесная
связь
между
множествами
эффеI{ТИВНЫХ
и
собственно
эффек
тивных
ТОЧeI"
при
водятся
оценки
числа
эффективных
ре
шениii
в
дискретных
задачах.
В
последнем
параграфе
дан
нраший
обзор
методов
построения
мпожества
эффеliТИВ
пых
решенпй
и
способов
проверIШ
эффективности
выде
лепного
решения.
Знание
структуры
п свойств
множества
эффеI\ТПВНЫХ
точек
«в
Целом»
для
различных
Iшассов
МIIОГОI\рнтерпаль
пых
задач
позволяет
глубже
нопять
спеЦПфlШУ
ЭТIIХ
за~
дач,
их
существенные
отличия
от
задач
с
одним
крите
рпt3м,
а
также
способствует
разработке
ЧIlсленных
ме
тодов
отыскания
всего
множества
эффеI\ТИВПЫХ
точек.
Отметим,
что
большинство
результатов
данной
главы
были
получены
совсем
недавно:
в
течение
последнего
дe~
сятилетия.
§
3.1.
ТопологичеСIше
свойства
~шожеств
эффективных
оцеНОI~
11
решений
В
пачале
параграфа
исследуется
вопрос
о
том,
когда
ыножества
эффеI\ТИВНЫХ
и
слабо
эффеI\ТИВНЫХ
точеI{
яв~
ляются
замкнутыми.
Далее
формулируются
условия,
при
I;OTOPblX
множество
собственно
эффективных
точек
плот~
по
во
множестве
эффективных
точек.
В
занлючение
раз~
бираются
достаточные
условия
того,
чтобы
множество
эффеI\ТИВНЫХ
точек
было
дугообразно
связным,
стягива~
емым
в
себе,
ретрактом.
1.
Понятно,
что
замкнутость
множества
эффеюивных
(в
том
пли
ином
смысле)
решений
существенным
образом

142
СТРУНТУРА
МНОЖЕСТ1ЗА
ЭФФЕКТИВНЫ}"
РЕШЕНИй
[ГЛ.
3
должна
быть
связана
с
замкнутостыо
самого
множества
Х
и
непрерывностью
/.
Для
слабо
эффективных
решений
эта связь,
нак
известно
([23]),
оказывается
достаточно
простой.
Т
е
о
р
е
м
а
1.
Если
множество
Х
вам1'>НУТО,
а
ве1'>ТОР
фУН1'>ция
/
неnрерывnа,
то
Sj(X)
ва.м1'mуто.
Д
о
н
а
з
а
т е
Л
ь
с
т
в
о.
Допустим,
что
множество
S/X)
не
замкнуто,
так
что
существует
последователь
ность
{x~)
~
Sj(X),
сходящаяся
J\
точке
хО
Е
X\Sj(X).
Сле
довательно,
найдется
точка х·
Е Х
такая, что
/(х*)
>
/(хО).
Тогда
благодаря
непрерывности
f
для
достаточно
боль
шого
номера
k
окажется,
что
/(х*)
>
/(x
k
),
а
это
ПрОТlIво·
речит
слабой
эффективности
x
R
• •
Если
в
этой
теореме
в
качестве
Х
взять
У,
а
вместо
f -
вектор-фуннцию
(У.,
Yz,
••• ,
Ут),
то
получим
условия
замкнутости
множества
S(Y).
С
л
е
Д
с
т
в
и
е
1.
Если
множество
оцено1'>
У
8a.~1'>HYTO,
7'0 •
.l-tnожесrво
слабо
эффеroтuвllЫХ
оцено"
S(
У)
также
sa.'Ill'mYTo.
Если
воспользоваться
теоремой
1.6.2,
в
которой
сфор
мулированы
достаточные
условия
совпадения
множеств
Pj(X)
и
Sj(X),
то
из
теоремы
1
получим
следующий
ре
зультат.
т
е
о
р
е
м
а
2.
Пусть
мnожество
Х
выnуro.ло
и
ааАmну
то,
а
веroтор-фуН1ЩUЯ
/
непрерывна
и
строго
roвазuвогну
та.
Тогда
множество
эффе1'>тивных
решений
Pj(X)
sаю~
нуто.
Требование
строгой
квазивогнутости
/
в
этой
теореме
существенио:
если
оно
не
выполнено,
то
даже
в
случае
т
= 2
множество
Pj(X)
может
оказаться
незамкнуты:\1.
При
м
1>
Р
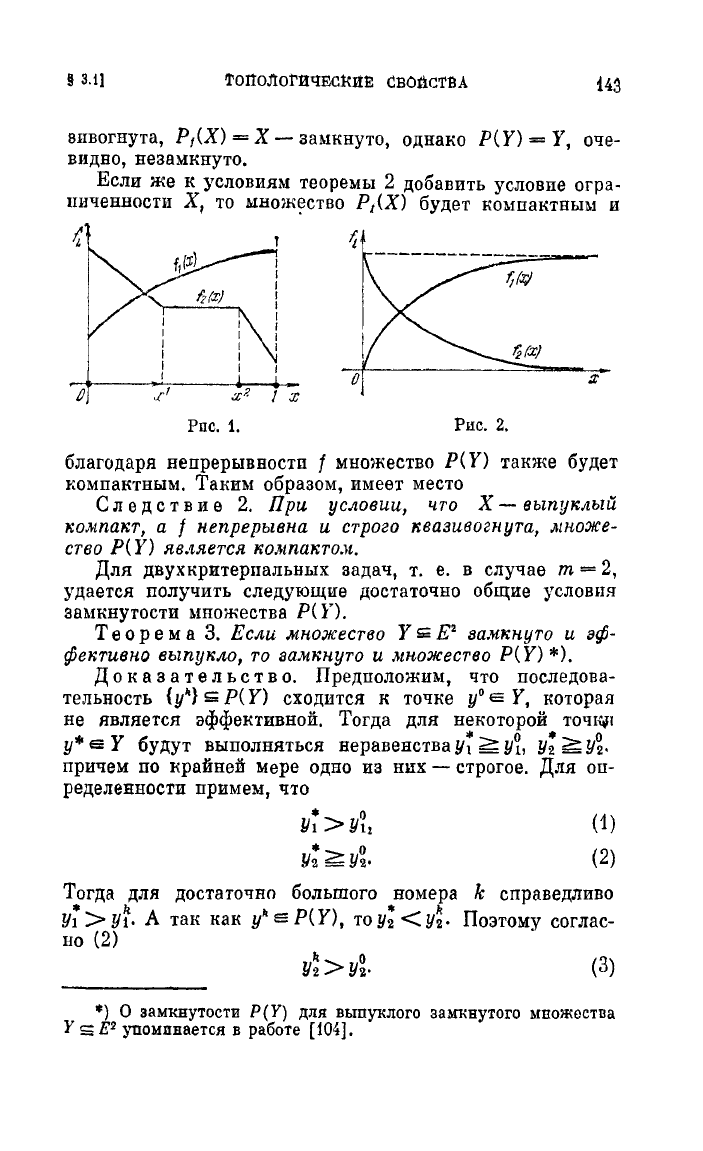
1.
Пусть
Х
=
[О,
1].
а
функции
/1.
/2
имеют
графики,
представленные
на
рис.
1.
Обе
фующии
кв&зи
вогнуты,
но
лишь
,.
строго
I\ВаЗIlвогнута.
Здесь
незамк
путав
множество
Pj(X)
является
объедиuением
двух
не
пересеRающихся
интервалов
[О,
х·)
и
[х
2
,
1].
Обратимся
к
вопросу
о
замкнутости
множества
эффет<
тивных
оценок.
Как
показывает
нижеследующий
пример,
множество
Р(
У)
может
оказаться
пезамlшуты:\1
даже
еСЮI
Pj(X)
замкнуто и
выполнены
все
преЦПОJlожения
тео
ремы
2.
При
м
е
р
2.
Пус1Ъ
Х
=
[О,
+ 00),
а
графики
фУШЩИЙ
,.
и
/2
изображены
на
рис.
2.
Здесь
/ =
(/1,
/2)
строго
ква·
s:щ
~оnологпqЕСНnЕ
СВОЙСТВА
143
8lIвогнута,
Pt(X) =
Х
-
замкнуто,
однако
Р(У)
=
У,
оче
видно,
незамкнуто.
Если
же
к
условиям
теоремы
2
добавить
условие
огра
ниченности
Х/
то
множ~ство
Р,(Х)
будет
Rо~шактным
и
---------------
Рис.
1.
Рис.
2.
благодаря
непрерывности
t
мноЖеСтвО
Р(
У)
таRже
будет
компактным.
Таким
образом,
имеет
место
С
л
е
Д
с т
в
и
е
2.
П
ри
условии,
что
Х
-
выnу~лый
~O,Mna~T,
а
t
непрерывна
u
строго
,.вазивогнута,
ЮiQже
ство
Р(
У)
является
nOMna~To.}t.
Для
двухкритериальных
задач,
т. е.
в
случае
т
=
2,
удается
получить
следующие
достаточно
общие
условия
замкнутости
множества
Р(
У).
Т
е
о
р
е
м
а
3.
Если
множество
У
s:
р
8a.'rtnHYTO
u
эф
феnтuв1iО
выnуnло,
ТО
ааМ1mуто
u
М1tDжество
Р(У)
*).
Д
о
к
а
з
а
т е
л
ь с
т
в
о.
Предположим,
что
последова
тельность
(уЧ
s:
Р(
У)
сходится
к
ТОЧRе
уО
Е
У,
Rоторая
не
является
эффективной.
Тогда
для
некоторои
ТОЧЩI
У*
Е
У
будут
выполняться
неравенства
у;
:>
Y~,
У:::>
y~.
причем
по
Rрайней
мере
одно
из
них
-
строгое.
Для
оп
ределенности
примем,
что
(1)
(2)
Тогда
для
достаточн()
большого
номера
k
справедливо
* k
А
~
Р(У)
* k
П
Уl
>
У
1.
так
как
у
Е
,
то
У2
<
У2'
оэтому
соглас-
но
(2)
(3)
*)
о
замкнутости
Р(У) ДЛЯ
выпуклого
замкнутого
мпожества
У
s:;;
Е2
упоминается
в
работе
[104].

144
СТРУКТУРА
МНОЖЕСТВА
ЭФФЕКТИВНЫХ
РЕШЕНИй·
[гл.
З
Для
любого
'(
Е
[О,
1/2]
у
()') = +
уО
+
(+
_
У)
у*
+
yyk
Е
У
* =
у
-
E~.
Отсюда
с
учетом
(1)
получаем
(О
1
о
1 *
11
у!
)
=ТУl
+
ту!
>Yl'
Следовательно,
для
достаточно
малого
'(
Е
(О,
1/2)
бунет
выполняться
У!
(у)
>
y~.
Кроме
того,
в
силу
(2)
И
(::Р
верно
У2
(у)
>
yg.
Поэтому
для
достаточно
большого
k
оказывается,
что
У('()
>
y~.
Поскольку
у('()
Е
У
* ,
то
су
ществует
ТОЧI\а
у
Е
У,
дЛЯ
которой
верно
у
~
У('().
Таким
образом,
у
>
У\
а
это
противоречит
эффективности
у"
.•
То,
что
в
доказанной
теореме
условие
т
= 2
является
существенным,
показывает
следующий
пример.
При
м
е
р
3.
Пусть
У
с
Е
Э
-
круговой
конус,
осно
ванием
которого
служит
единнчный
круг
в
плоскости
удУ2,
а
вершиной
точна
А
=
(О,
1,
1)
(см.
рис.
3).
Для
рассматрп
ваемого
множества
У
все
точни
дуги
DC
В
(кроме
точки
В)
эффек
тивны.
Чтобы
убедиться
в
этом,
достаточно
заме
тить,
что
для
любой
внутренней
точки
этой
дуги
существует
опор
ная
к
множеству
У
Рис.
3.
плоскость,
которая
пер-
пендикулярна
некото-
рому
вектору
с
положительными
компонентами
(это
вле
чет
даже
собственную
эффективность).
Точка
D
эффек
тивна,
так
как
является
единственной
точкой
из
У,
име
ющей
наибольшую
координату
УI
=
1.
Однако
точка
В
не
эффективна,
так
как
А
=
(О,
1,
1)
>
(О,
1,
О)
=
В.
Подобно
тому
как
в
теореме
3
были
получены
усло
вия
замкнутости
Р(
У),
можно
доказать
следующпе
ус
ловия
заМЮlУТОСТII
Р/(Х)
дЛЯ
двухкритериальных
зада'!.

§ 3.1)
топологnqЕСНИЕ
СВОйСТВА
145
т
е
о
р
е
м
а
4.
Если
множество
Х
выпукло
и
заМКllУ
ТО,
а
вектор-функция
f = (/1, /2)
вогн.ута
и
непрерывна
на
Х,
ТО
.МНОжество
Pj(X)
замкнуто.
Заметим,
что
в
отличие
от
требования
строгой
ква
зивогнутости
j
теоремы
2,
здесь
предполагается
вогну
тость
j,
т. е.
теорема
4
определенным
образом
дополняет
теорему
2
в
случае
т =
2.
2.
Следующая
теорема
устанавливает
тесную
взаимо
связь
множества
эффентивных
и
множества
собственно
эффективных
оценок.
Д. А.
Молодцовым
[58]
она
была
получена
при
более
ограничительных
предположениях.
т
е
о
р
е
м
а
5.
П
редnоложuм,
что
множество
У
замк
llУТО
и
существуют
вектор
1.1.
Е:М
и
число
CG
та",ие,
ЧТО
<~t,
У)::;;
CG
для
всех
у
Е
У.
(4)
Тогда
ссу)
ПЛОТНО
в
Р(У),
Т.
е.
C(Y)5OP(Y)5OC(Y).
(5)
Доназательство.
Поскольну
внлючение
C(y)s;;;
50
Р(
у)
имеет
место
всегда,
остается
убедиться
в
справед
ЛИВОСТII
внлючеппя
Р(
У)
50
С(
N.
Это
ВIшючеНlIе,
очевид
но,
выполняется,
если
Р(У)
=
е5.
Пусть
у
О
Е
р(у).
Не
уменьшая
общности,
будем
считать,
что
у
О
>
0<,1'1)'
Дока
жем
существование
последовательности
собственно
эф
феl{ТlIВНЫХ
точен,
сходящихся
к
уО,
Введем
функции
P~
(у)
=
(1
-
т;:
1 )
Yi
+
~.
У1
t
19'1
i =
1,
2,
,
..
,
т;
k =
т,
т
+
1,
.,.,
I!
рассмотрим
замкнутые
множества
Qh
=
У
n
(у
Е
Е
m
I
P~
(У
-
уО)
>
о,
i =
1,
2,
' ,
'1
т),
k = m
1
т
+
1"'"
Понятно,
что
Qm
:2
Qт+1
:2
Qт+2
:2
, , •
Благодаря
условию
(4)
найдетоя
та
НОЙ
номер
kO,
что
все
множества
Qn,
k
~
kO,
I\оМП8НТНЫ,
Функции
minл~F~
(У),
k =
kO,
kO
+
1,
"'];
iEM
10
В.
В.
Подиноесrшi1.
В.
д.
Ногин

148
С1'РУНТУРА
МНОЖЕСТВА
ЭФФЕНТИвных
РЕmЕнйй
[l'Л.
з
где
л~
=
Р:
~yO)
/,~
р7
~yO)
>
01
непрерывны
на
Ет
по
у.
Поэтому
для
каждого
k =
kO,
kO
+.
+
1,
,
..
найдется
такая
точка
уА
Е
Qя,
что
min
лfF~
(yli) >
min
л~F~
(у)
(6)
ieM ieM
для'
всякого
у
Е
QA,
В
том
числе
и
для
уО.
Если
же
у
6
Е
Y\QA,
то
для
некоторого
i
справедливо
неравенство
F~
(уО)
>
F~
(у).
Поэтому
и
min
л~
F~
(уО)
>
min
л~
F~
(у).
iEM
iEM
Следовательно,
неравенство
(6)
имеет
место
для
всех
у
Е
У.
Это,
согласно
следствию
2.1.6,
влечет
уА
Е
G(
У).
Так
как
при
любом
k
~
kO
верно
Qk
~
QkO'
то
{у"}
f:
~Qko,
k =
kO,
k
O
+
1,
....
Но
Qk
o
-
компакт,
и
поэтому
из
последовательности
{уА}
можно
выделить
подпоследова
тельность,
сходящуюся
к
некоторой
TOQKe
у*
Е
У.
Сог
ласно
определению
множеств
QA
число
k
можно
выбрать
так,
чтобы
произвольная
точка
из
QA
(в
том
числе
и
уА)
была
приближена
к
множеству
уО
+
E~
с
любой
наперед
заданной
точностью.
Следовательно,
у*
Е
уО
+
Er;.
А
так
как
уО
Е
Р(
У),
то
у*
=
уО.
• -
Для
выпуклого
множества
У
теорема
5
справедлива
без
условия
(4).
Т
е
о
р
е
м
а
6.
Если
.множество
У
BaMroHYTO
и
8ЪZnУ1i,ЛО,
7'0
справедливы
в1>лючения
(5).
Д
о
к
а
з
а т
е
л
ь с т
в
о.
Условие
(4)
в
доказательстве
теоремы
5
использовалосъ
лишь
для
уст~новления
огра
ниченности
множеств
QA'
начиная
с
неноторого
k.
Если
же
У
ВЫПУRЛО,
то
выlIRлыы
и
Qk' k =
т,
т
+
1,
•••.
Когда
хотя
бы
одно
из
множеств
Qm, Qm+t,
•••
оказывается
ог
раниченным,
то
доказательство
проходит
далее,
как
в
теореме
5.
Остается
выяснить,
возможен
ли
случай,
когда
все
QA
неограничены.
В
таном
случае
для
каждого
k
можно
УRазатъ
точку
уА
Е
Qk,
принадлежащую
сфере
еди
ничного
ради)'са
с
центром
в
точке
уО,
Благодаря
ком-
§ 3.IJ
ТОПОЛОГИЧЕСКИЕ
СВОЙСТВА
147
пактности
сферы
из
последовательности
{yk}
можно
вы
брать
подпоследовательность,
сходящуюся
к
точке
у*
Е
Е
У.
Но
тогда
у*
Е
уО
+
Е";
и
у*
+
уО,
что
противоречит
эффективности
уО.
Следоваftшьно,
если
У
выпукло,
то все
множества
Qл
неограни
ченными
быть
не
могут.
•
Требование
ВЫПУRЛОСТИ
У
в
последней
теореме
является
существенным;
об
этом
свидетельствует
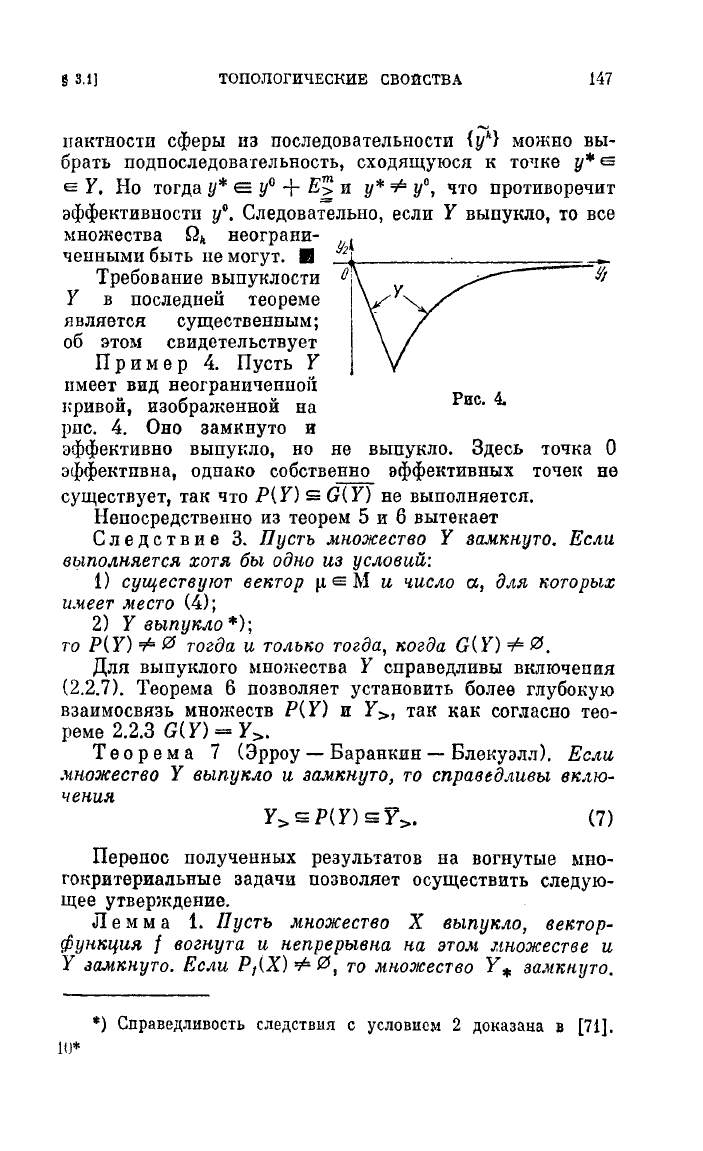
Пример
4.
Пусть
У
имеет
вид
неограниченноii
I,РИВОЙ,
изображенной
на
рис.
4.
Оно
заминуто
и
Рис.
4.
эффективно
ВЫИУl:ЛО,
но
не
выпукло.
Здесь
точка
О
эффективна,
одиако
собственно
эффективных
точен
не
существует,
так
Что
Р(У)
s;
G(
У) не
выполняется.
Непосредственно
из
теорем
5
и
6
вытекает
С
л
е
Д
с
т
в
и
е
3.
Пусть
,м,/1,ожество
У
аа.м.х/1,УТО.
Если
выполняется
хотя
бы
од/1,О
из
условии:
1)
существуют
вептор
J.t
Е
М
и
число
сх,
для
которых
U.чеет
место
(4);
2)
У
выnу/'i,ЛО
*);
то
Р(
У)
+
J25
тогда
и
толbl'i,о
тогда,
погда
G(
У)
+
J25.
Для
выпуклого
множества
У
справедливы
включепия
(2.2.7).
Теорема
6
позволяет
установить
более
глубокую
взаимосвязь
множеств
Р(
У)
и
У
>,
таи
как
согласно
тео
реме
2.2.3 G(
У)
=
У>.
Те
о
р
е
м
а
7
(3рроу
-
Баранкин
-
БлеRУЭЛЛ).
Если
.11,/1,ожество
У
eblnYIr,.!lO
и
aa.м.Ir,HYTO,
то
справедливы
в/'i,ЛЮ-
че/1,ия
(7)
Перепое
полученных
результатов
на
вогнутые
м:но
ГОRритериальные
задачи позволяет
осуществить
следую
щее
утверждение.
Л
е
м м
а
1.
Пусть
множество
Х
выnу/'i,ЛО,
вептор
фУ/1,/'i,ция
f
вогнута
и
непрерывна
/1,а
ЭТО.ftt
J.tножестве
и
у
аа.м.пнуто.
Если
Р,(Х)
+
JO,
то
Jotножество
У
*
за.ftt/'i,н,уто.
*)
Справедливость
следствия
с
условием
2
доказана
в
[71].
10*

148
СТРУНТУРА
МНОЖЕСТВА
ЭФФЕl\ТIIВНЫХ
РЕШЕНИй
[гл.
3
Д
о}\
а
з а
т
е
л
ь
с
т
в
О.
Возьмом
произвольную
сходя
щуюся
последовательность
{уЧ
из
У
*:
yk
.......
у,
yk
~
fCr
h
),
x
h
Е
Х,
k =
1,
2,
...
(8)
Без
ограничения
общности
моншо
считать,
что
у
=
Ор,,).
Для
до}\азательства
справедливости
леммы
предположим
противное:
О(m)
Ф.
у
*.
Возможны
два
случая:
послеДова
4
тельность
{f(x
k
)}
ограничена,
либо
не
ограничена.
Если
вир
Ilj{xk)11
~
а
для
а
Е
[О,
+ 00),
то
из
последо-
k
nатеЛЬНОСТll
{j{x~)}
можно
выделить
сходящуюся
подпос
ледовательность
{/{x
1
)},
внеравенстве
yl:S:;
f{x
1
)
перейти
к
пределу
при
Z
.......
00
и
благодаря
зам}\нутости
У
полу
ЧIIТЬ
О(m)
<
Нт
/(x
1
)
=
у*
Е
У.
Тан
}\а}\
у*
Е
У,
то
найдет
ся
такая
точка
х*
Е
Х,
что
у*
=
/(х*).
ТаЮIМ
образом,
О(m)
~
/(х*),
а
это
противоречит
предположению
O(Тn)
Ф.
Ф.
у*.
Пусть
последовательность
{/<x
k
)}
пе
ограниченu.
В
этом
случае
в
силу
(8)
ТОЧI{И
/<x
k
)
при
неограниченпом
увеличении
k
СI\ОЛЬ
угодно
БЛИЗI{О
приближаются
}\
неот-
рицательному
ортанту
E~.
При
необходимости
переiiдя
1;\
последовательности,
мощно
считать,
что
последоnатеJlЬ
пость
{11/{xk)lI}
строго
возрастающая
и
вир
/1
(х
п
)
= +
00,
/1
(хН!)
>
/1
(х"),
k =
1)
2)
...
" .
/2(Xh)~
-
О,
вир
/i
(х")
>
01
k
i =
3,
4,
"',
m.
(9)
По
условию
леммы
Р
/Х)
=f=
(25,
и
поэтому
наiiдется
Х
О
Е
Pj{X).
Начиная
с
HeIiOToporo
номера,
иоследователь
ность
{lIf{x
k
)
- j(X°)IJ}
должна
стать
строго
возрастающей
II
положительной.
Не
уменьшая
общности,
будем
СЧIlтаТf"
что
этот
номер
-
первый.
Воаьмем
0<8
< II/{x
l
)
-
/<xO)II.
В
силу
непрерывности
j
для
I{aiНДОГО
k
можно
УI,азать
та}\ое
Лk
Е
(О,
1),
что
(10)
Благодаря
вогнутостн
j
имеем

§
З.1)
ТОПОЛОГИЧЕСКИЕ
СВОйСТВА
Отсюда
и
из
(10)
следует
z~
::::;;;
fi
(х
О
)
+
В,
i =
1,
2,
...
, m.
14\:1
(
12)
С
другой
стороны,
в
силу
(9)
начиная
с
неIЮТОРОГО
k
бу
дут
выполняться
неравенства
f.(x
h
)
~
-
Е,
i =
1,
2,
...
, m.
Поэтому
получаем
Z~>-tЛIi+(1-Лk)fi(хО)f
i=1,2,
...
;m.
(13)
Перавенства
(12)
и
(13)
указывают
на
ограниченность
последовательлости
{Zk},
и
поэтому
ее
можпо
считать
схо
дящеЙся.
Последовательность
{ш"} в
силу
того,
что
име
ет
место
равенство
(10)
тан:же
будем
СЧIlтать
сходя
щеЙся.
Докажем,
что
Лk
~
о.
Для
последоnaтельпости
{z~1
б.lIагодаря
(12)
и
(13)
мошна
написать
Iz~1
<::
с,
где
с
б;
о.
Используя
определение
z~
(11),
отсюда
получаем
с
+ I
/1
(х
О
)
I
Л/i
<:: .
= 1/1
(х")
-
/1
(xO)I'
oТI,yдa,
согласно
первой
стj:ЮI\е
пз
(9)
следует
Лk
-+
о.
1'аЮIМ
образом, из
(13)
вытеиает
перавенство
Нт
Zh
г
~
j(XO).
Поэтому
благодаря
(11)
II
(10)
получаем
шО
=
=
liш
ш
•
б;
f(xO)
И
шО
=1=
j(XO).
Причем
всле)1ствие
заМЮlУ
тости
У
верно
шО
Е
У,
т. е.
существует
тю,ая
тОЧЮ}
х'
ЕХ,
ЧТО
f(x')
=
шО
?f(xO).
Это
противоречит
эффективно
сти
хО
.•
Если
в
этой
лемме
вместо
Х
взять
У.
а
в
Юlчестве
f -
линейную
вентор-функцию
(У"
Yz,
••• ,
У".),
то
полу
чим
следующее
утверждение.
С
л
е
Д
с т
в
и
е
4.
Если
У
-
выnуw,лое
заNl>нуrое
J1t1{I)-
жесrво
u
Р(
У)
=1=
Ф,
то
,мложество
У
*
аа;.mн,уто.
Следует
отметить,
что
следствие
4
в
случае,
когда
У
Зill\ПШУТО
и
лишь
эффеIПИВIlО
выпуI{ЛО,
ОI,азывается
не
верным
(см.
при
мер
4).
В
следующей
теореме
утвеРII\ДеПIlЯ
теорем
6
и
7
IIС
реносятся
на
вогнутые
МПОГОI,ритериальные
задачи.
т
е
о
р
е
1\1
а
8.
Пусть
Х
выnу".ло,
веI>ТОР-фУ/i"'ЦUЯ
f
вoгnYTa
u
непрерывна
на
Х,
а
У
за;.uщуrо.
Тогда
спра
ведливы
61>лючения
(5)
и
(7).
Д
о
R
а
з
а т
е
л
ь
с т
в
о.
Согласно
леммам
2.2.2
и
1,
У
* -
ВЫПУI{лое
заl\IIшутое
множество.
Примеплл
1\
этому

150
струнтур
А
МНОЖЕСТВА
ЭФФЕКТИВНЫХ
РЕШЕНИй
[ГЛ,
3
множеству
теорему
6,
получим
G
(У*)
s;
Р(У.)
s;
G
(У
.)t'
откуда
с
учетом
леммы
2.2.1
вытекают
требуе:м:ые
вклю
чения
(5).
Если
же
к
множеству
У.
приМенить·
тео
рему
7
и
воспользоваться
легко
проверяемым
равенством
(У
*»
=
У
>1
то
получим
включения
(7)
.•
Заметим,
что
условие
замкнутости
У
теоремы
8
за
ведомо
выполняется,
если
Х
-
компакт,
а
j
непрерывна
на
Х.
Перейдем
от
оценок
к
решениям.
В
условиях
теорем
6
Il
8
правое
IlЗ
ВRлючений
(14)
может
ОRазаться
не
справедливым.
При
м
е
р
5.
Пусть
Х
с:
Е
3
-
круговой
нонус,
основа
нием
которого
служит
единичный
круг
в
плосности
х
1
Ох
2
,
а
вершиной
-
точка
А
=
(О,
1,
1).
Это
множество
можно
считать
нзображенным
на
рис.
3,
если
заменить
на
нем
YI.
Yz,
Уз
соответственно
на
XI,
X
z
,
X
s
•
Для
j(x)
=
(x
1
•
х
2
)
множеСТВО~1
Gj(X),
очевидно,
будет
дуга
окружности
DCB
(без
нонцевых
точек
D
и
В),
а
множество
Pj(X)
будет
состоять
из
той
же
дуги
(ВIшючая
точки
D
и
В)
и
отреЗl\а
АВ.
Следовательно,
здесь
Gj(X)
не
покрывает
всего
множества
Pj(X).
Условия
справеДJIИВОСТИ
включеппй
(14)
формулиру
ются
в
следующем
утверждении.
С
л
е
Д
с
т
в
и
е
5.
Если
Х
-
выnуnлый
nомnак,т,
а
j
вогнута
и
непрерывна
на
Х,
nричеАt
хотя
бы
oaT-tа
КО.лt
nонеnта
I1
строго
вoгnYTa,
то
справедливы
вnлючения
(14).
Д
о к а
3
а
т е
л
ь
с т
в
о.
Возьмем
произвольное
решение
х
О
е
Pj(X).
Согласно
теореме
8
существует
такая
ПОCJIе
довательность
{x~},
что
j(x~)
-+
l(xO)
Il
х'
е
G
j(X)
для
лю
бого
k = 1, 2,
.•.
ПОСRОЛЬНУ
Х
!(омпактно,
эту
последо
вательность
можно
счптать
сходящейся:
Нт
хп
=
х*
Е
Х.
k
....
oo
Очевидно,
I(x·)
=
j(XO).
Если
х*
'*
хО,
то
благодаря
вог
нутости
и
строгой
вогнутости
для
л
е
(О,
1)
имеем
f(лх*
+
(1-
л)х
о
)
>
лf(х*)
+
(1-
'}Jj(XO)
=
j(XO),
Это
неравенство
противоречит
условюо
хО
Е
Р/(Х).
Сле
довательно
х*
"'"
хО,
•
