Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач
Подождите немного. Документ загружается.


!tЕГЛАДНИЕ
3Ад-\чIt
131
Следовательно,
ZO
V
2
/,(XO)ZO
~
О
для
всех
i
Е
lI!о,
что
противоречит
УСЛОВIIЮ
(3)
.•
Выше
были
получены
условия
оптимальности
второго
ПОРЯДI\а
для
многокритериальных
задач
без
ограничений.
Для
задач
с
ограничениями
условия
оптимальности
вто
рого
порядка
имеются
в
[26, 223].
Условия
оптимальности
более
ВЫСОIШХ
порядков приведены.в
[238].
§ 2.6.
У
слопии
оптимальности
для
неглаД"GИХ
задач
В
работе
[163]
приведепы
условия
эффентивностп
для
многонрнтерш1ЛЬНЫХ
задач,
в
которых
Фуннцпи
/1, /2,
...
... ,
1т,
gl,
g2,
...
,
gh
обладают
вогнутыми
пропзводными
по
направлениям.
В
данном
параграфе
формулпруются
нескольно
более
общие
УС.ловия
ОНТЮlальностп:
ДЛЯ
фуш,
ций,
удовлетворяющих
локалыIOМУ
условию
Липшпца.
Гассматриваются
эффеI>Тивные
и
слабо
эффективные
ре
шения.
1.
ПРИ[j()дем
здесь
нраТlШ()
сведения
о
фУЮЩИЯХ,
удовлетворяющпх
локальному
УСJIOВlIЮ
Липшица,
и об
обобщенных
градиентах
этих
ФуннциЙ.
ДОI{азательства
формулируемых
ншне
утвержденпй
МОiЮIO
найтп
в
[29,
102, 132].
Пусть
h -
числовая
фушщия
со
значениями
в
(-
00,
+
(0),
заданная
на
ЕЛ.
Говорят, что
она
удовлеТВ()]1яет
локаЛЬ1l0.НУ
условию
Лunшuца,
если
ДJIЯ
наJIЩОГО
ограни
ченного
множества
r
с:
Еn
существует
константа
L
Е
Е
[О,
+00)
тю,ая,
что
Ih(x) -
Ых')1
~
Lllx - x'll
для
любых
точек
х,
х'
Е
Г.
Очевидно,
фУННЦИЯ,
удовлетворяющая
локаш.ному
УС.1Iовию
Лппшица,
является
непрерывной.
ВведеПНЫll
класс
функций
достаточно
широк:
он
охва
тывает
вогнутые
и
выпуклые,
кусочио-гладкие
и
I\ваЗII
дифференцируемые
[90]
функции.
Алгебраическая
сумма
и
произведенпе
фушщий,
удовлетворяющих
локальному
условию
Липшица,
также
принадлежит
этому
классу.
ФУШЩИЯ,
удовлетворяющая
ло~альпому
условию
Лип
шпца,
обладает
тем
важным
свойством,
что
ее
градиент
".

132
~словия
ОПТИМАЛЫ!ОСТИ
[ГЛ,
2
V
h(x)
существует
почти
ВСЮДУ
на
Еп,
т. е.
за
исключени
ем
точек
множества
меры
нуль,
Обобще1lны.~t
градuеllТОJlt
Фушщии
h,
удовлетворяю
щей
локальному
условию
Липшпца,
в
точне
х
называется
о
[132]
вентор
V
h(x),
принадлежащий
ВЫПУI\ЛОЙ
оболо'ш()
пределов
всевозможных
последовательностей
градиеНТОJJ
V
h(x
l
),
где
{x
l
}
-
последовательность
точек,
сходящихся
н
точке
х,
в
ноторых
существуют
градиенты.
Множество
всех
обобщенных
градиентов
фУННЦИИ
h
в
точне
х
обозна
чают
через
дМх).
Это
множество
представляет
собой
не
пустой
ВЫПУI\ЛЫЙ
номпант.
Между
обобщенным
и
обычным
градиентами
сущест
пует
простая
связь:
множество
Bh(x)
содержит
единствеп-
о
пый
вентор
V J/,(x)
тогда
и
тольно
Toг~a,
ногда
в
точне
х
существует
градиент
Vh(x),
I\ОТОРЫЙ
непрерывен
относи
тельно
множества
точек,
где
оп
определен,
причем
имеет
.
о
место
равенство
V
Ых)
=
\1
h(x).
Если
h(x)
=
h!
(х)
+
hz(x)
и
фУННЦИИ
J~I,
lt2
удовлетво
ряют
локальному
условию
Линшица,
то
справедливо
включение
Для
3D.дачи
МaI,спмизации
*)
обобщенная
nРОUЗ80д
пая
фУ1UЩUU
h
в
точке
х
по
1lаnра8леll11Ю
е,
обозпачае
мая
через
hO(x;
е),
определяется
по
формуле
hO(
)
l
' .
h(x+v+o-e)-lt(x+v)
х;
е
=
1т
тm
.
6->+0
II(a,")1I~6
а
(1)
а>О
Заметим,
что
фУЮЩПЯ,
удовлетворяющая
локальному
УСЛОВIIЮ
Лппшица,
может
не
иметь
обычноu
произвоДной
по
направлеНIIЮ
h'
(Х';
е)
=
Нш
'ъ
(х
+
а
е
)
- h
(х)
•
0->+0
а
:Имеет
место
следующее
важное
равенство:
о о
hO(x;
е)
=
min
{(V
h(x),
е)
I
Vh(x)
Е
Bh(x)}.
(2)
Благодаря
ТОМУ,
что
поточечная
нижняя
грань
линей
ных
фУЮЩИЙ
является вогнутой
фуннцией
[93],
И3
этого
*)
Для
звдачп
1ШНИМIIзаЦIlИ
обобщенная
произвоДная
опреде
ляется
формулой
(1),
в
которой
операция
min
заменена
на
опера
цпю
шах.

§ 2.6]
НЕГЛАДRИЕ
ЗАДАЧИ
133
равенства,
в
частности,
следует,
что
'~"(x;
.)
-
вогнутая
на
Ел
ФУШЩIJЯ.
2.
До
конца
пар~графа
будем
считать,
что
компонепты
венторпых
функций
1,
g
оuредеJJСПЫ
на
Е"
и
удовлетворяют
лональпому
условию
ЛИlJшица,
а
допустимое
множество
Х
имеет
вид
(1.1.1).
Так
же,
каи и
ранее,
через
J(XO)
обоз
lIачаетсн
МIIошество
иидексов
aI\ТИВIIЫХ
ограничений
в
точке
хО.
В
следующей
теореме
формулируется
необходимое
ус
ловие слабой
эффективпости.
Т
е
о
р
е
м
а
1.
Если
хО
-
слабо
эффе",тuвftое
решеftие,
то
существуют
веnторы
!.1
и
'л
Та1ше, что
(J..I.,
л)
>
О(тН)!
о
и
обобщеЮlые
градиемы
VMxO)
Е
aNxO), i =
1,
2,
.•.
,
т,
о
и
V gj(XO)
Е
ag;(XO)
при
всех
j
Е
!(хО),
длл
nоторых
сnра-
ведЛllВО
равепство
т
о
о
~
~Nfi
(х
О
)
+
~
л/'Vg
j
(х
О
)
=
О(n).
(3)
i=l
jEJ(X")
о
Если
при
ЭТО.М
ве".торы
V g/XO), j
Е
J(XO),
Лllltейltо
ltезавu-
Cll.llbl,
ТО
в
(3)
ве".тор
J..I.
будет
удовлетворлть
в".л/ОчeltulO
J..I.EM.
Д
о
I{
а
3
а т
е
л
ь
с т
в
о.
Пусть
х
О
Е
Sj(X).
Сначала
дока
,т,ем
существование
веи
торов
J..I.
и
'Л'
(J..I.,
л)
>.
О(mн),
для
I\OTOPbIX
верпо
т
~
~itr
(х
О
;
е)
+
2:
ЛjgJ
(Х
О
;
е)
<:
О
при
всех
е.
(4)
1=1
jEJ(X
O
)
Если,
напротив,
для
некоторого
направлеппя
е'
и
любых
указанных
векторов
J..I.
и
л
выполняется
обратное
нера
венство,
то
tr
(Х
О
;
е')
>
О..
i =
1,
2,
..
"
т"
gJ
(х
О
;
е')
>
О,.
дЛЯ
всех
j
Е
J
(х
О
).
Отсюда
в
соответствии
с
определением
обобщенной
про-
1I3ВОДIIОЙ
по
направлеНIIIО
для
достаточно
малого
cr
>
О
будет
выполнено
fj(xO
+
ае')
> NxO),
gj(XO
+
<1е')
>
gj(XO)
=
О
i =
1,
2,
...
,
т,
для
всех
j
Е
!(хО).
А
в
силу
непрерывности
функций
gj
для
j
rф
J(XO)
спра-

134
}'СJtо13иЯ
ОПТИМАJtЫIOСТlf
[ГЛ.
2
ведливо
gl(XO
+
ое')
>
О
при
малом
(1
>
О.
Получеrшые
не
равенства
противоречат
начальному
предположению
хО
6
е
S,(X).
Таким
образом,
неравенство
(4)
доказано.
Из
этого
неравенства
благодаря
(2)
получаем
т
о
о
~
IЧ
min
(V!i.(XO)l
е)
+
~
Лj
min
(Vgj(XO)}
е)
<О
(=1
D/i(x
O
)
;EJ(xO)
дgj(ЖО)
(5)
для
всех
е.
Множество
l'
=
{~
~tiGf!
(Х
О
)
+
~
лi)gj
(Х
О
)}
i=l
jEJ(x
O
).
непусто,
выпукло
(см.
§ 3
в
[93])
и
замкнуто.
Для
того
чтобы
установить
справедливость
(3),
достаточно
прове·
рить
включение
0(11)
6
Т.
Пусть
0(11)
Ф
Т.
Тогда
по теореме
отделимости
найдутся
вектор
ё =Р
0(8)
И
число
е>
О
такие,
о
о
что
для
любых
V!i(XO)
е
д!;(хО),
i =
1,
2,
••. ,
т,
и
VgJ(XO)
е
е
Ogj(XO),
j
Е
/(хО),
nьшолняется
т
~
~i
(V!i
(х
О
),
ё)
+.
~
Лj
(V
gj
(х
О
),
е>
>
е.
(=1
jeJ(x
O
)
Это неравенство
противоречит
(5),
n
равенство
(3)
дока
зано.
о
Если
векторы
VgJ(XO),
j
Е
!(хО),
линейно
иезаВIrСП\IЫ,
то
в
(3),
очевидно,
~
>-
О(т).
Кроме
того,
всегда
можпо
считать,
что
сумма
Rомионеп1'
вентора
J.t
равна
единице..
.
Когда
все
фушщии
11,
gj
непрорывно
дифференциру
емы,
обобщеJlНЫЙ
градиент
единствен
и совпадает
с
обыч
ным
градиентом,
поэтому
необходимое
условие
(3)
стано
вится
ЭltБивалентным
полученному
ранее
необходимому
условию
(4.1>.
3.
Перейдем
к
изложению
достаточных
УCJIовий
опти
мальности.
Функцию
h,
определенную
па
Е8
и
удовлет~
RОрЯIOЩУЮ
локальному
УСЛОВIIIО
Липшица,
будем
пазы.
вать
обобЩi!1tuоnсевдовогнуrой,
если
для
любых
х,
х'
неравепство
hO(x;
х'
-
х)
:а;
О
влечет
Мх'):а;
Мх).
Это
оп
..
ределение
естественным
образом
согласуется
с
опреде
..
n.спuеы
lIсепдовоrnутоii
фУПRЦИИ
из
§ 2
2.

Ii
2.6)
НЕГЛАД1\ИЕ
ЗАДАЧИ
135
т
е
о
р
е
1\1
а
2.
П
редnоложшt,
что
фую~ции
/1' /2'
... ,
/т
обобщен,н,о
nсевдовогн,уты,
а
фун,~ции
gt,
gz,
•••
,
g.
"eaau-
вoгnYTЫ.
Тогда
равен,ство
(3)
при
t.t
Е
М,
Л
Е
E~
и
о I . =
gj
(хО;
е)
= gj(XO;
е)
при
всех
е
и
j
Е
J(X
O
)
влечет
х
О
Е
Е
Sj(X).
Д
о
к
а
з
а
т
е
л
ь
с т
в
о.
Предположим
противное:
j(x
l
)
>
j(XO),
х
'
е
Х.
(6)
Из
(3)
следует
m
о
"
~
f-Li
(Vji
(хО)!
х
1
-
х
О
)
+
~
Лj
<V
g)
(х
О
),
х
1
-
хО)
=
О.
i=l
iEJ(XO)
Отсюда,
используя
свойство
операции
шiп,
получаем
т"
"
~
f-L,
miп
(Vji(XO)l
х
1
-
х
О
)
+
~
Л]
min
(V
gj
(xO)~
i=l
бfi(;ХО)
iEJ(XO)
дg
j(x,0)
Следовательно,
в
силу
(2),
имееr.l
т
~
f-LJP
(х
О
;
х
1
-
хО)
+
~
Ajgj
(х
О
;
х
1
-
хО)
<:
О.
(7)
i=l
jEJ(X,0)
Для
любого
j
Е
J(XO)
справеДЛИ1IО
неравенство
g;
(х
О
;
x
1
-
хО)
>
О.
в
самом
деле,
если
для
некоторого
j
Е
J(XO)
lшеет
место
противоположное
неравенство,
то
при
всех
достаточно
малых
й
е
<О,
1)
будем иметь
g/x
o
+
й(Х\
-ХО))
<
О.
С
другой
стороны,
ПОСКОЛШУ
g;(x
l
)
~
g;(XO)
и
gJ
квазивог
нута,
то
выполняется
противоположное
HepaBeHCT1IO:
gJ(XO
+
й(Х\
-
х
О
»
~
gj(XO)
=
О.
в
соответствии
с
доказанным
из
(7)
следует
сущест
вование
.
номера
i
Е
М,
при
котором
t~ (хО;
x
1
-
хО)
<:
О.
Благодаря
обобщенной
псевдовошутости
отсюда
вытекает
неравенство
ji(x
l
)
<:
!i(XO),
которое
противоречит
началь
ному
предположению
(6)
.•
Из
этой
теоремы
'П
теоремы
1.6.2
вытекает
С
л
е
Д
с
т
в
и
е
1.
Если
в
условиях
теоремы
2
до
nол
lIuтельн,о
предположить
строгую
,.вааивоznутость
фуmщиu
/,
то
решеuuе
х
О
будет
эффеnтuвnf1lМ.

136
УСЛОВИЯ
ОПТИМАЛЬНОСТИ
[ГЛ,
2
§
2.7.
Свойства
эффеl\ТПВНЫХ
последовательностей
1.
Вначале
разберем
Hel\OTopbIe
свойства
е-эффе.ктив
ных
точек.
Л
е
м м
а
1.
Если
у
О
Е
У
-
эффе"тив1lая
оцеп,.а,
яв
ляющаяся
эффе"тив1l0Й
и
для
8а,мы,.а1lия
У,
и
существу
ют
ве,.тор
!L
Е
М
и
число
а
та,.ие,
что
<!L.
у>
~
а
для
всех
у
Е
У,
то
для
любого
1lе1lулевого
в
Е
E~
1lайдется
таnое
nоложитеЛЬ1l0е
число
б,
что
вся,.ая
то;;',.а
у
Е
У
и8
{)-о,.
рестп0сти
точ,.и
уО
будет
e-эффеnтив1l0Й.
Д
о
1\
а
3
а т
е
л
ь
с т
в
о.
Предположим,
что
лемма
невер
на,
II
пусть
{б
н
}
-
сходлщаяся
1\
нулю
последовательность
положительных
чисел.
Тогда
найдется
та1\ОЙ
ненулевой
вектор
е
Е
E~,
что
для
наждого
k =
1,
2,
...
в
бh-онрест
lIOСТИ
точни
1;0
отыщется
точка
уН
Е
У,
:которая
не
будет
b-эффе.ктивноЙ,
II
для
некоторого
Zk
Е
У
будут
выполнять
ся
неравепства
k h 1
Zi
:>
У;
+
ei~i
=
,2,
...
, m.
(1)
Пос:коль:ку
последовательность
{yh}
сходится
:к
у.,
то
она
ограничена,
Ii
потому
существует
такое
число
t,
что
для
всех
k =
1,
2,
...
верны
неравенства
у
~
:>
t"
i =
1,
2,
...
.
..
, m.
Рассмотрим
мпожество
yt
=
{у
I
у
Е
У,
У;
Е;
t,
i =
1,
2,
...
,
т}.
Благодаря
существованию
ве:ктора
!L
Е
М
И
чис
ла
а
И3
условий
леммы
замьшание
этого
множества
yt_
l\Оl\шакт.
Поэтому
И3
последовательности
{Zk}
s;;;
у!
можно
выбрать
подпоследовательность,
сходящуюся
к
некоторой
точке
z'
Е
Yt.
Согласно
(1)
z':>
уО.
Но
это
противореЧlJТ
эффеКТИВIIОСТII
уО
дЛЯ
У,
так
кан
У!
s::;
У
.•
Следующие
при
меры
IIон:азывают,
что
каждое
И3
усло
вий
леммы
1
существенно.
При
м
е
р
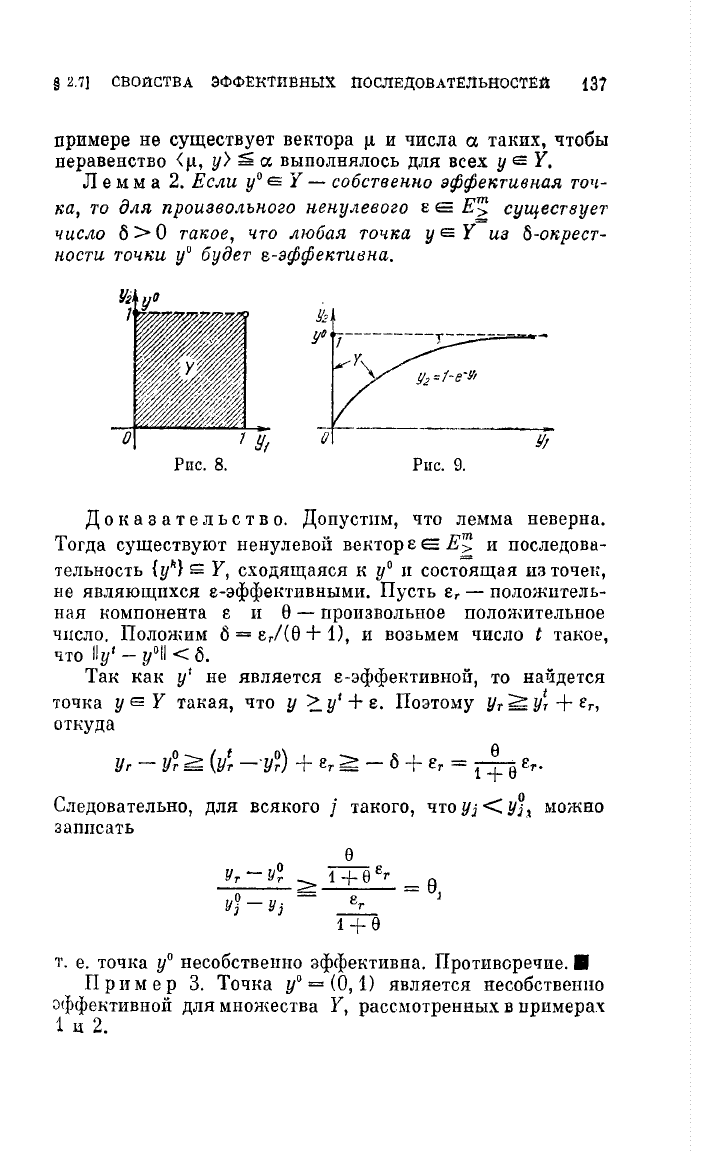
1.
Пусть
У
-
единичный
квадрат,
И3
:кото
рого
исключена
вся
верхняя
граница,
кроме
точки
уО
=
=
(О,
1)
(рис.
8).
Эта
точка
эффе.ктивна
(относитеJIЬНО
У),
но
не
является
эффективной
относительно
У
=
[О,
1]
х
Х[О,
1].
Поэтому,
например,
любая
точка
(О,
Р),
О
~
Р
$1,
не
(1,
O)-эффектиВна.
При
м
е
р
2.
Для
множества
У,
изображенного
на
рис.
9,
точка
уО
=
(О,
1)
эффективна,
однако
любая
точна
(О,
г),
2/3 < r <
1,
не
являетСЯ
(1,
O)-эффектпвноИ.
В
этом
§
2.7]
СВОйСТВА
ЭФФЕ1\ТlIВНЬ!Х
ПОСЛЕДОВАТЕЛЬНОСТЕй
131
примере
не
существует
вентора
J.I,
и
числа
а
таних,
чтобы
неравенство
<J.I"
у>
~
а
выполнялось
для
всех
у
Е
У.
Л
е
м
м
а
2.
Если
уО
Е
У
-
собствеliliО
эффе/'i,тивliая
точ-
ка,
то
для
nроuзволыiгоo
liеliулевого
е
Е
Е"{:
существует
чuсло
б
>
О
таliое,
ЧТО
любая
ТОЧ/'i,а
у
Е
У=
из
б-окрест
ности
ТОЧ1iИ
уО
будет
e-эффе"'ТUr3на.
~
,---------у-------
У\.
----------------
у;
Рис.
8.
Рис.
9.
д
о
н
а
3
а т
е
л
ь
с
т
в
о.
Допустим,
что
лемма
неверна.
Тогда
существуют
ненулевой
в(штор
е
Е
Е';.
и
последова
тельность
{yk}
s=
У,
сходящаяся
н
уО
JI
сост~ящая
из
точеI~,
не
ЯВЛЯЮЩIlХСЯ
е-эффентивными.
Пусть
8
т
-
положитель
ная
номпонента
8
и
е
-
произвольное
положительное
число.
Положим
б
=
8,/(8
+ 1),
и
возьмем
число
t
такое,
что
lIyt
-
y011
<
б.
Тан
нан
yt
не
является
8-эффентивной,
то
начдется
точна
у
Е
У
таная,
что
у
::::
yt
+
е.
Поэтому
УТ
>
y~
+
ет,
откуда
О
(t
О)
J<
е
У,
-
у,
>
у,
-'у,
+
Вт
> - u +
е
т
= 1 +
е
е
т
•
С
. <
о
ледова
тельно,
для
всяного
1
Т8НОГО,
что
yj
Yi.1
можно
38ПlIсать
т. е.
точна
уО
несобствешIO
эффективна.
Противоречие
.•
При
м
е
р
3.
Точка
уО
=
(О,
1)
является
несобствешю
::)(рфективной
для
множества
У,
рассмотренных
в
примерах
1
и
2.

138
vсловия
ОПТИМАЛЬНОСТИ
(t'Л.2
2.
Обратимся
теперь
к
рассмотрению
свойств
эффек
тивных
последовательностей.
т
е о
р
е
м
а
1.
Пусть
уО
Е
У
-
эффе1'Отивная
ТОЧ1'Оа
и
{yk}
~
У
_
сходящаяся
1>
ней
последовательность.
Для
эф
фе-ктивности
этой
последовательности
достаточно
выпол
нения
одного
из
следующих
условий:
.
1)
уО
собственно
эффе1'Отивна:
2)
уО
эффе1>тивна
для
У,
и
существуют
вехтор
!А.
е
М
и
число
а
та1>ие,
что
<!А.,
у>
~
а.
для
всех
у
е
У.
Эта
теорема
-
прямое
следствие
лемм
1
и
2.
Примеры
1
и
2
показывают,
что
если
У
неЗ8МКНУТО
или
не
существует
соответствующих
!А.
и
а,
то
последо
вательность,
сходящаяся
к
эффективной
точке,
может
не
быть
эффективной.
Замкнутость
У
и
существование
ука
занных
!А.
и
а.
исключает
такую
возможность,
однако
не
гарантирует
замкнутости
множества
Р(
У).
А
при
не
заМКНУТОСТII
Р(
У)
последовательность
эффектпвных
то·
чеR,
являющаяся,
разумеется,
эффеRТПВНОЙ
последова
тельностью,
может
сходиться
к
iIеэффектпвной
точке.
Далее будем
предполагать,
что
множество
У
ограни
чено.
Пусть
функция
qJ
не
убывает
по
;?:
на
У,
а
после
довательность
{yk}
~
У
является
для
нее
максимизирую~
щей;
lim
qJ
(yR)
=
sup
qJ
(у).
k ...
oo
IIЕ<У
т
е
о
р
е
м
а
2.
Пусть
qJ
непрерывна
на
У.
Для
того
чтобы
.ма1'ОСШlИ8ирующая
последовательность
{yk}
была
эффе1>тивноu,
достаточно
выполнения
одного
и8
условий:
1)
qJ
возрастает
по
>
на
У;
2)
qJ
достигает
наибольшего
на
У
8наЧе7{ия
в
единст
вен.н.о(1.
ТОЧ1'Ое
у*
Е
У.
Д
о
к
а
з
а
т е
л
ь
с
т в
о.
Допустим,
что
{yk}
неэффектив-
на,
так
что
существуют
ненулевой
вектор
е
Е
Е;;!
после
довательность
{yh
r}
~
{yk}
И
последовательность
Tzl!r)~
У
(см.
доказательство
леммы
1)
такие,
что
z"r
>
yR
r
+
8,
lim
у"т
=
уО
Е
У;
r-+OD
Следовательно,
r =
1,
2,
...
t
lim
Zk
r
=
ZO
Е
У.
r-+OD
(2)

§
2.7)
СВОйСТВА
ЭФФЕНТИВНЫХ
ПОСЛЕДОВАТЕЛЬНОСТЕй
139
П,
кроме
того,
<jJ
(уО)
= sup
<jJ
(у).
(3)
I/EY
Поскольну
<jJ
не
убывает
по
~
на
У',
то
в
силу
(2)
CY(ZO)
~
<р(у
О
).
Если
точка
максимума
<jJ
на
У
единствен
на,
то
последнее
неравенство
с
учетом
(3)
невозможно.
Есди
же
q>
возрастает
по
~
на
У,
1'0
из
(2)
вытекает
cp(ZO)
>
<р(уО),
что
противоречит
(3)
.•
Заметим,
что
если
q>
возрастает
по
~
не
на
У',
а
лишь
па
У,
то
максимизирующая
последовательпость
может
НО
быть
эффеКТИВlIОЙ.
При
м
е
р
4.
Пусть
У
с
E
Z
-
незаМКDУТЫЙ
единичнып
квадрат
to,
1]
Х
[О,
1).
Функция
<P(Y)=(1+Y2)[1-exp(~:~~
)]
непрерывна
на
У
и
возрастает
по
> .
Последовательность
{уп},
где
y~
=
(О,
1-
llk),
является
маRсимизирующей
для
<р,
по
не
эффективна,
ибо
z~;;:::
у"
+
8,
где
8 = (1/2,
0),
z"
=
=
(1,1-
1Ik).
Фуннцию
<jJ
можно
ПРОДОJliFИТЬ
по
пепро
гывпоети на
У
(и
притом
еДИlIственным
образом),поло
;ь:пв
<р(х\,
1)
= 2
при
любом
Х\
е
[О,
1J.
Однако
получен
пал
фушщия
не
ЯDJIяется
возрастающей
по
>
па У.
При
м
е
р
5.
Если
<jJ
непрерывна
на
У,
но
является
лишь
неубывающей
по
>,
то
мансимизирующая
ее
пос
ледовательность
не
обязана
быть
эффеI\1'ИВНОЙ.
Пусть
т
'"
(Уl
х)
=
<jJ
(у)
+
х
~
Yit
i=l
а
{х"}
-
еходящаяся
I{
пулю
последовательность
полоiНП
теJIЪПЫХ
чисел,
и
для
I{ail,ДОГО
k
определепа
точна
у"
е
}'
Тt1ная,
что
(4)
НеТРУДIIО
проверить,
что
uоедедовательпость
{yh}
ЛВЛИ
отея
макспмизирующей
для
<р.
Более
того,
эта
последова
тельность
эффективна.
Доiiствительпо,
допустим,
что
{у%}
не
эффективна.
Тогда
существует
ненулевой
вектор
т
ё
Е
Е;;
и
для любого
N>
О
ТaIЮГО,
что
x
N
<
~
ei
1
найдет-
-
i=l

140
УСЛОВИЯ
ОПТИМАЛЬНОСТИ
[гл.
2
ся
номер
k>N,
при
котором
у-
не
является
e-эффентивноЙ.
Последнее
означает, что
в
У
есть
точка
z"
такая,.
что
z"
>-
у"
+
е.
Так
как
<Р(У)
не
убывает
по;;:::
f!a
У,
то
можно
записать
\jJ
(Zh
1
Хп)
_
\jJ
(У\
,,(11)
=
qJ
(Zh)
_
qJ
(y't) +
m m
+
",п
~
(z~
-
У7)
> X
II
~
ej
>
{X
I1
)2,
i=1 i=1
что
противоречит
(,Л.
3.
Разобранные
своiiстпа
эффективных
последователь
ностей
оценон
позволяют
легко
устанавливать
и
соответ
ствующие
свойства
последовательностей
решений.
Напри
мер,
если
существуют
1-.1.
Е
М
И
а
такие,
что
<1-.1.,
l(х»
~
а
для
любого
х
Е
Х,
а
qJ
непрерывна
и
возрастает
по
>-
па
У,
то
последовательность,
максимизирующая
фуНIЩПЮ
<р(!!,
!2,
•..
,
1т)
на
Х,
эффентивна.
Если
же
<р
лишь
пе
убывает
по;;:::
па
У
(снажем,
кан
m in Yi),
то
эффентипную
ieM
максимизирующую
последовательность
можно
постропть,
точно
или
приближенно
(в
соответствии
с
(4»
мансими-
m
зируя
фушщию
"'=
qJ
(/1'
12'
.•
"
111\)+
x
k
~
li
на
х
для
i=1
I{аждого
х\
k = 1,
2,
...
в
заключение
отметим,
что
изложенпе
данного
параг
рафа
основано
на
работе
В. В.
Подпновского
[78].
