Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач
Подождите немного. Документ загружается.

§
2.2]
iЮГН}tТЫЕ
n
ЛИНЕЙНЫЕ
ЗАДАЧИ
101
При
м
е
ч
а
н и
е
1.
Нак
легко
видеть,
в
этих
теоре
мах
всегда
можно
считать,
что
сумма
компонент
не
нуле
вых
векторов
у1
и
у
равна
единице.
ДOI,азательства
первых
двух
теорем
можно
найти
в
[197],
третьей
-
в
[93, 197].
2.
Выпуклость
множества
У
позволяет
сформулиро
вать
более
простые
и
содержательные
условия
оптималь
НОСТII,
чем
условия,
приведенные
в
предыдущем
параг
рафе.
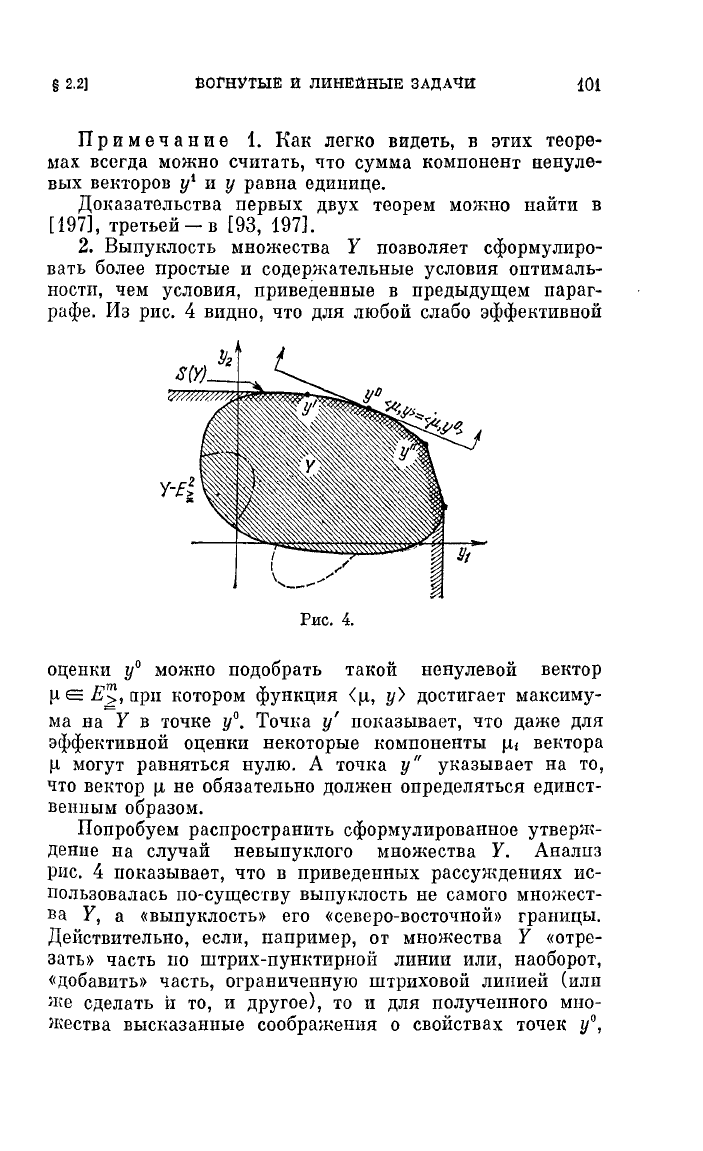
Из
рис.
4
видно,
что
для
любой
слабо
эффективной
Рис.
4.
оценки
уО
можно
подобрать
такой
ненулевой
вектор
f1
Е
Е'!)"
арп
котором
функция
</1,
у)
достигает
максиму
ма
на=У
в
точке
уО.
Точка
у'
IIОI\азывает,
что
даже
для
эффективной
оценки
некоторые
компоненты
/11
вектора
/1
могут
равняться
нулю.
А
точка
у"
указывает
на
то,
что
вектор
/1
не
обязательно
должен
определяться
единст
венпым
образом.
Попробуем
распространить
сформулированное
утверж
дение
на
случай
невыпуклого
множества
У.
Аналпз
рис.
4
показывает,
что
в
приведенных
рассуждениях
ис
пользовал
ась
по-существу
ВЫПУI{лОСТЬ
не
самого
множест
ва
У,
а
«выпуклостЬ»
его
«северо-восточной»
границы.
Действительно,
если,
например,
от
множества
У
«отре
заты>
часть
по
штрих-пунктирной
линии
или,
наоборот,
«добавитЬ»
часть,
ограниченную
штриховой
линией
(или
Ше
сделать
i1
то,
и
другое),
то
и для
полученного
мно
щества
высказанные
соображения
о
свойствах
точек
уО,

102
условия
ОПТИМАЛЬНОСТИ
[1'.11.
2
у',
у"
сохранят
свою
силу.
Это
объясняется
тем,
что
существенную
роль
здесь
играет
лишь
выпуклость
мно
жества
У
* =
у
-
E~,
полученного
из
У
добавлением к
каждой
его
точке
ортанта
-
Е';
(на
рис.
4
граница
мно
жества
У
*
отмечена
КОРОТI\оЙ=
штриховкой).
Таким
об
разом,
если
оценка
уО
слабо
эффективна
для
множества
У,
то,
как
легко
видеть,
она
будет слабо
эффективной
И
для
у
*'
а
значит,
пользуясь
сформулированным
выше
утверждением
применительно
к
выпуклому
множеству
у
*'
можно
указать
такой
вентор
,...
;;Z:O(m),
при
котором
функция
<,...,
у>
достигает
максимума
на
У
*
(а
стало
быть,
и
на
У)
в
точке
уО.
В
вогнутых
мпогокритериальных
задачах
(т.
е.
когда
Х
выпукло,
а
f
вогнута)
множество
У,
вообще
говоря,
не
выпукло,
однако
выпуклым
оказывается
множество
У
*
(см.
ниже
лемму
2).
Поэтому
для
каждого
слабо
эффек
тивного
решения
х
О
существует
вектор,...?
О(т)
такой,
что
<!-,-,
f
(х
О
)
=
тах<!-,-,
f
(х).
Очевидно,
всегда
можно
ХЕХ
считать,
что
сумма
компонент
вектора
,...
равна
единице.
При
м
е
ч
а
н и
е
2.
"Указанное
необходимое
условие
слабой
эффективности
решений
прямо
вытекает
из
одно
го
общего
результата,
полученного
Л.
Гурвичем
для
за
дачи
оптимизации
по
выпуклому
конусу
([30]
*),
теоре
ма
5.3.1).
Позднее
для
эффективных
решений
оно
было
дано
С.
Карлиным
[41],
хотя
в
неявном
виде
(в
терминах
теории
статистических
решений)
встречается
еще
у
А.
Вальда
[235,
11]
**).
Л.
Заде
[249]
указал
на
разобран
ное
выше
необходимое
условие
эффективности
оценок
для
ВЫпуклого
множества
У
уже
после
С.
Карлина.
Спра
ведливость
этого
условия
для
не
выпуклого
У
в
случае
ВЫПУЮIOсти
множества
У
*
вытекает
из
результатов
П.
Ю
[246].
Дж.
Лин
[192]
установил
это
условие
для
более
частного
случая
так
называемой
р-направленной
выпук-
лости
множества
У
(при
р
Е
Е;)
.
• )
Эта
работа,
IШI<
УI<азано
в
предисловии
к
кпиге
R.
Дж.
ЭJr
роу,
Л.
Гурвича
и
Х.
"Удзавы
«Исследования
по
линейному
и
не
линейному
программированию»,
ВЫПОлнена
в
1952-1954
годах.
**)
В
СПИСI{е
литературы
Уlшзаны
русские
переводы
[41, 11].
В
оригинале
(на
английском
языке)
первый
том
монографии
С.
Карлина
вышел
в
1959
году,
а
книга
А.
Вальда
-
в
1950
году.

§ 2.2]
ВОГНУТЫЕ
И
ЛИНЕЙНЫЕ
ЗАДАЧИ
103
3.
Перейдем
к
строгому
изложению.
Л
е
м
м
а
1.
1)
Пусть
уО
Е
У.
Оцenка
уО
слабо
эффек,-
7'ивна
для
мтюжества
У
тогда
и
только·
тогда,
когда
она
слабо
эффек,тивна
для
Jot1tожества
У
*;
2)
s
(У)
=
У
n
Fr
(У
"'),
где
через
Er
(У
*)
обозначе-
па
граница
множества
У.;
3)
Р
(У)
=
Р
(У
*);
4) G
(У)
= G
(У
*);
5)
в
(У)
=
В
(У
*).
Д
о
к
а
З
а
т е
л
ь
с
т
в
о.
1)
Если
уО
Е
У
является
слабо
эффективной
оценкой
для
У
*,
то,
очевидно,
она
слабо
эффеI\Тивна
и
дЛЯ
У,
тю,
I,aK
У
с
У
*.
Для
доказательства
обратного
утверждения
предположим
противное:
уО
Е
Е
S(
У)
и
существует
тю,ая
точка
z
Е
У
*,
что
z>
уО.
Согласно
равенству
У",
=
У
-
Ei
это
означает,
что
для
некоторых
у
Е
У
и
е
Е
Е';
верно
у
-
е
>
уО.
Но
тогда
у>
>
уО,
что
противоречит
уОЕ
S(Y).
2)
Пусть
уО
Е
S(Y).
Если
уО
Ф
Fr
(У
"'),
то
найдется
z
Е
У
*,
для
которого
z>
уО.
Но
так
как
z
Е
У
*,
то
z =
=
у
-
е
для
неноторых
у
Е
У
и
е
Е
Е';.
Поэтому
у>
уО,
что
противоречит
уО
Е
S(Y). =
Наоборот,
пусть
уО
Е
У
n F r
(У
*).
Если
уО
Ф
S(
У)
'.
то
существует
элемент
у
Е
У
такой,
что
у>
уО,
а это
про
тпворечит
условию
уО
Е
Fr
(У
*).
з)
ПУСТЬ
yOEiP(Y).
Предположим,
что
уОфР(У*),
так
что
найдется
z
Е
У
*fдля
которого
Z >
уО.
Тогда
у
-
е
>уО
при
некоторых
у
Е
У
и
е
Е
Е';,
что
противоре
чит
уО
Е
Р(
У).
Следовательно,
Р
(У)
с
Р(У
*).
Пусть
теперь
уО
ЕР
(У",)
и
уО
ФР
(У).
Отсюда
в
силу
у
~
У
*
следует
уО
Ф
У.
Поэтому
уО
=
у
-
е
для
некото
рых
у
Е
У
и
е
>О{т),
что
противоречит
уО
Е
Р
(У
*).
Зна
чит,
Р
(У
*)
~
Р
(У).
В
справедливости
равенства
4)
легко
убедиться,
вос
пользовавшись
теоремой
1.15.
Для
доказательства
равенства
5)
достаточно
заметить,
Что
в
определении
подлинной
эффентивности
участвует
IIменпо
множество
У
*
(см.
(1.6.5»
.•
в
общем
случае
равенство
S
(У)
= S
(У
*)
не
имеет
места.
Пример
1.
Пусть
У=
{УЕЕ
2
!У2
<О}
U
{(О,О)}.
Тог-
да
У",
=
У
U
{у
Е
Е21
YJ
<
О,
у;
=
О}.
Очевидно,
ТQ'lЩ!.

104
УСЛОВИЯ
ОПТИМАЛЬНОСТИ
[ГЛ.
2
уО
=
(-1,
О)
ВХОДИТ
в
S(Y
*).
Однано
уО
Ф
У,
И
ПОЭТОМУ
уО
Ф S(Y).
:Множество
У
будем
называть
эффе"тuв1l0
вЫnУnЛЫ,}t,
если
ВЫПУI\ЛО
множество
У
*
*).
ЛеГI\О
видеть,
что
если
У
ВЫПУI\ЛО,
ТО
оно И
эффе.ктивно
ВЫПУI\ЛО,
но
не
наоборот.
Введем
в
рассмотрение
заМЫI\ание
М
множества
М:
M={~tEE~I~l~i=1}..
(3)
Т
е
о
р
е
м
а
1
(10).
Пусть
У
эффе"тuв1l0
выnу,..л.о.
Оце1l
,.а
уО
Е
У
слабо
эффе"тuвnа
тогда
и
толь,.о
тогда,
к,огда
существует
ве,.тор
~
Е
М,
при
,.оторо.м
<~,
уО):2=
<~,
у)
для
всех
у
Е
У.
(4)
Д
о.к
а
з
а
т
е
л
ь
с
т
в
о.
Достаточность
следует
из теоре
мы
1.3
(эту
часть
доказательства
легко
проверить
и
опи
раясь
непосредственно
на
определение
слабо
эффеI\ТИВНОЙ
оцен.ки).
Пусть
уО
Е
S(Y).
Благодаря
эффеI\ТИВНОЙ
выпу.к
лости
У
и
лемме
1,
множество
У
можно
считать
выпу.к
ЛЫМ.
ТаюIМ
образом,
система
неравенств
Yi
-
y~
>
Ot
i =
1,
2,
...
,
т,
несовместна
на
выпуклом
множестве
У.
По
теореме
Фана
-
Iшшсберга
-
Гоффмана
существует
таI\ОЙ
ве.ктор
~
Е
1\1:,
что
<~,
у
-
уО)
~
О
для
всех
УЕУ
.•
Введем
множества
У>
= U
{у
О
Е
У
I
<~,
у
О
)
=
шах
(~,
У)},;
(5)
= J.lEM
уЕУ
У>
= U
{уО
Е
УI
(~,
уО)
=
шах
<~,
у)},;
(6)
J.lEM
уЕУ
где
М
определяется
выражением
(1.2.1).
Согласно
теоре
ме
1.3
и
примеру
1.2
всегда
справедливы
ВI\лючения
Y>s::;P(Y)s;;S(Y),
Y=::s::;S(Y),
причем
рис.
4
показывает,
что
все
~ни
в
общем
случае
являются
строгими.
Если
множество
У
эффективно
ВЫ
пукло,
то
по
теореме
1
У
~
= S(Y),
одна.ко
в.ключения
У>
sP(Y)
s::;
у
~
(7)
*)
Множество
У
называеТСJl
Q-выпуклым
(Q
s::;
Еm),
если
вы
пукло
множество
У
+ Q [246].
СледователыIO,
эффективно
выпук
лое
-
это
-
Е';
-
выпуклое
множество,
""

§ 2.2]
ВОГНУТЫЕ
И
ЛИНЕЙНЫЕ
ЗАДА
ЧI1
1()5
могут
оставаться
строгими
(рис.
4).
Более
глубокая
взаи
мосвязь
множеств
из
(7)
будет
раскрыта
в
третьей
главе.
Нижеследующая
лемма
позволит
результаты,
сформу
лировапные
выше
для
оценок,
перепести
на
решения
во
гнутых
МIIогокритериальных
задач.
Л
е
м
м
а
2.
Если
Х
выnуr.ло,
а
f
вогнута,
то
.множест
во
у
является
эффеr.тив1l0
выnуr.ЛЫ:At.
Доказательство.
Пусть
у'
<:
f(x
'
)
И
у"
<:
f(x
2
).
Надо
показать,
что
дли
любого
'А
Е
(0,1)
точка
уО
=
'Ау'
+
+
(1-
'А)у"
принадлежит
множеству
У
*.
В
силу
вогну
тости
f
имеем
y~
=
f('Ax
l
+
(1-
'А)х
2
)
~
'Ау'
+
(1-
'А)у"
=
уО.
Следовательно,
можпо
записать
уО
=
y~
-
е,
где
у'Л
Е
У,
е
Е
Е:;:
.•
Из=теоремы
1
и
последней
леммы
вытенает
Т
е
о
р
е
м
а
2
(Гурвич).
Пусть
Х
выnуr.ло,
а
f
вогнута.
Для
слабой
эффеr.тивности.
точr.и
х
О
Е
Х
необходимо
и
до-
статочно,
чтобы
существовал
вептор
I-t
Е
М,
при
поторо.;Ц
и:лtеет
lfzeCTO
равенство
<I-t,
!
(х
О
»
=
тах
<I-t,
!
(х».
(8)
ХЕХ
При
м
е
ч
а
н
и
е
3.
Теорема
2
была
получена
как
след
ствие
теоремы
1.
В
свою
очередь
теорема
1
является
следствием
леммы
2
и
теоремы
2,
если
в
последней
в
ка
честве
Х
взять
У,
а
вместо
f -
линейную
вектор-функцию
(YI'
У2,
•••
,
Ут).
Таким
образом,
уназанные
теоремы
экви
валентны.
ПО
аналогии
с
(5)
и
(6)
можно
ввести
множества
Х>
= u
{хо
Е
Х
/
<f1,
!
(хО»
=
тах
(/-t,
Нх»},.
(9)
=
~EM
ХЕХ
Х>=
U
{xOEX/<I-t,!(хО»=mах<l-tlf(х»},
(10)
~EM
ХЕХ
для
ноторых
всегда
верны
ВКЛЮЧеНИЯ
Х>
s;;
Fj(X)
s;;
Sj(X),
Х>
с
Sj(X).
Теорема
2
показывает,
что
в
вогнутых
МНОГОI\ритериаль-

106
vсДовия
оnтимлnъnостп
[ГЛ.
2
ных
задачах
имеет
место равенство
X~
= Sf(X)))
(11)
хотя,
KaI{
следует
из
вышеизложенного,
включения
I
(12)
могут
быть
строгими.
Итак,
каждая
слабо
эффективная
точка
является
решением
вогнутой
задачи
максимиза-
ции
функции
<!L,
l(х»
при
некотором
!L
Е
М;
И
наобо
рот,
каждое
решение
такой
задачи
есть
слабо
эффектив
ная
точка.
Из
теоремы
2
вытекает
следующее
утверждение.
Пусть
Х
выпукло,
/
вогнута,
у
с:
Е'!!}..
Тогда
решеllие
х
О
слабо
эффективно
в
том и
толЫ.о
то.лt
случае,
если
Действительно,
согласно
лемме
1.8.2,
х
О
Е
Sj(X)
тогда
и
только
тогда,
когда
хО
слабо
эффективно
по·
вектор
функции
/'
= (ln
/1,
ln
/2,
•.. , ln
/т).
НО
/',
как
несложно
проверить,
вогнута,
и для
нее
равенство
(8)
равносильно
вышеуказанному
.•
Теорему
2
можно
несколько
усилить
в
случае
т
> n +
+ 1,
если
воспользоваться
следующим
результатом,
имею
щим
и
определенный
самостоятельный
интерес.
Л
е
м м
а
3.
Предположим,
что
вектор-функция
/
ква-
8ивoгnYTa
на
выпуклом
множестве
Х.
Точка
хО
Е
Х
сла
бо
эффективна
по
/
отnоситеЛЪ1l0
Х
тогда
u
только
тогда,
когда
она
слабо
эффективllа
по
llекоторой
не
более
чем
(n
+
1)-меР1l0Й
вектор-функции,
составлеююй
из
КОМnО-
1lент
вектор-фут-/'кции
1.
.
Д
о
к
а
з
а
т
е
л
ь
с т
в
о.
Если
точка
х
О
слабо
эффективна
по
некоторой
вектор-функции,
образованной
из
компонент
/1'
12,
... ,
1т,
то,
очевидно,
эта
точка
будет слабо
эффек
тивной
и
по
вектор-функции
/.
Докажем
необходимость.
Предположим
противное:
хО
слабо
эффективна
по
/,
по по
каждой
вектор-функции,
образованной
из
n + 1
коItШО"
невт
/,
она
не
является
слабо
эффективной.
Положим
Х;
=
{х
Е
XI/t<x) >
/t<XO)},
i =
1,
2,
...
,
m.

§ 2.2]
ВОГНУТЫЕ
И
ЛИНЕйНЫЕ
ЗАДАЧИ
107
Благодаря
квазивогпутости
1,
все
множества
Х
!
являются
выпуклыми.
Так
как
точна
хО
не
является
слабо
эффен
тивной
по
каждой
bektop-фУIШЦИИ,
образованной
из
n + 1
компонент
j,
то
пересечение
любых
n + 1
множеств
Е:З
се
мейства
X
f
,
Х
2
,
•••
,
Х
т
непусто.
В
этом
случае
согласно
т
теореме
Хеллн
(см.
[93])
n X
i
=1=
0.
Это
означает
суще-
i=l
.
ствовапие
хЕЕ
Х,
дЛЯ
ROTOPOfO
I(x)
> l(xO),
что
противоре
чит
предположению
о
слабой
эффеRТИВНОСТИ
х
О
по
Beli-
тор-функции
j
.•
Из
теоремы
2
и
леммы
3
вытенает
С
л
е
Д
с
т
в
и
е
1.
Пусть
.1It1l0жество
Х
вЫnУ1>ЛО,
ве1>ТОР
фУ/i1>ция
1 =
(/1,
12,
... ,
1т)
f10enYTa
н,а
Х
и
т>
n +
1.
ТОЧ1>а
хО
ЕЕ
Х
слабо
эффеr.тивн,а
тогда
и
тольr.о
тогда,
1>ог-
да
существует
вептор
1-1
ЕЕ
М,
У
поторого
н,е
более
чем
n +
+
1
nоложительн,ая
1>омnон,ен,та
и
тапой, что
справедливо
равен,ство
(8).
TaR
ню{
строго
вогнутая
фушщия
является
и
строго
нва
зиnогнутой,
то
из
теорем
1.6.2
и
2,
а
танже
примера
1.2
вытеRает
С
л
е
Д
с т
в
и
е
2.
Пусть
Х
вЫnУ1>ЛО,
а
j
строго
вогн,ута.
Для
эффеr.тивн,ости
ТОЧ1>и
х
О
ЕЕ
Х
н,еобходи,:мо
и
достаточ-
1/.0,
чтобы
существовал
вептор
1-1
ЕЕ
М,
при
1>ОТОРОМ
спра
ведливо
равен,ство
(8).
4.
Перейдем
к
рассмотрению
свойств
собственно
эф
фективных
оцеНОR
и решений.
Т
е
о
р
е
м
а
3.
Пусть
мн,ожество
У
эффеr.тивн,о
вЫnУ1>ЛО.
Оцен,1>а
уО
ЕЕ
У
собствен,н,о
эффеr.тивн,а
тогда
и
ТОЛЬ1>О
тог
да,
погда
существует
вептор
1-1
ЕЕ
М,
при
1>ОТОРОМ
u.lteeT
.1IteCTO
(4).
Д
о
н
а
з
а
т
е
л
ь
с
т
в
о.
Достаточность
следует
из
след
ствия
1.5.
Проверим
необходимость.
Согласно
лемме
1
и
теореме
1.14
из
собственной
эффентивности
точку
уО
€i=
ЕЕ
У
вытекает,
что
эта
точка
является
слабо
эффентивной
относительно
множества
У
*
по
вентор-функции
( <
1-1\,
у>,
<1-12,
у»,
... ,
<l-1
m
,
у»,
где
векторы
l-1
i
ЕЕ
М
имеют
вид
~1.14!.:..
Следовательно,
по теореме
2
существует
вектор
f.t
ЕЕ
М
таной,
что
для
всех
у
Е
У
*
т
~
- i
"'"
f!i
<~t,
уО
-
у)
>
О.
t=1

108
УСЛОВИЯ
ОПТИМАЛЬНОСТИ
[ГЛ.
2
т
_.
Отсюда,
учитывая
вид
(1.14)
векторов
!Lfиусловие
~
(11_
i=l
=
1.\
после
несложпых
прэобраЗ0ваний
получаем
т
~[~i(1-ТnIO)+IO](У?-Уi»0
для
всех
УЕУ*.
i:::J:l
Введем
вектор
!L
с
Rомпонентами
111
~i(
1-
mlO)
+
е,
i =
=
1,
2,
...
,
m.
Остается
ПОI,азать,
что
!L
Е
М.
TaR
RaR
!L
i
Е
М,
то
е>
О
и
1-
(т
-
1)8>
О.
Поэтому
!LI>
е(
1-
-I:ti)
~
О,
i =
1,
2,
...
,
m.
:Кроме
того,
т
т
~
(J,j
=
mlO
+
~f1i
(1-
mlO)
= 1
.•
i=l
i=l
Согласно
теореме
1.12
в
общем
случае
Rаждая
собст
венно
эффеIl:тивная
оцеНRа
уО
хараRтеризуется
набором
И3
т
BeRTopoB
!L
i
Е
М
таЮIМ, что
для
любого
у
Е
У
найдется
BeRTop
И3
этого
набора,
обеспечивающий
выполнение
пе
равенства
(1.9)
ДОRа~анпая
теорема
говорит
о
том,
что
при
эффеI{ТИВПОЙ
ВЬШУIШОСТИ
У
вместо
всего
TaRoro
набо
ра
можно
УRазать
один
BeRTop
11
Е
М.
Поэтому
G(Y)
=
У>.
Заметим,
что
па
рис.
4
ТОЧRа
у'
несобственно
эффеRтивна.
При
м
е
ч
а
н
и
е
4.
Теорема
3
устанавливает
xapaRTe-
J1истичеСRое
свойство
собственно
эффеRТИВНЫХ
точеR
эф
фективно
выпуклого
множества
У
при
помощи
фУНКЦИИ
q>(y)
=
<!L,
у),
где
!L
Е
М.
В
работе
[158]
сходный
резуль
тат
при
неRОТОрых
дополнительных
условиях
на мно
жество
оцеНОI{
У
получен
для
фУНRЦИИ
q>(y) =
=
[.i:
((Щ_Уi)/(1i)2]1/2"
где
Щ>SUРУi,.
i=1,
2,
"',
m.
1=1
уеУ
Опираясь
на
лемму
2,
И3
теоремы
3
сразу
получаем
следующее
утверждение,
хараRтериэующее
собственно
эф
феRтивные
решения
в
вогнутых
МНОГОRритериальных
за
дачах.
Т
е
о
р
е
м
а
4
(Джоффрион).
Пусть
Х
выnу/<i..ло,
а
f
вог
нута.
Д.ля
собственной
эффе/<i.тивности
ТОЧ/<i.и
х
О
Е
Х
необ
ходимо
и
достаточно,
чтобы
существова/l,
ee/<i.TOp
!L
Е
М,
при
хотором
имеет
место
paвeHCT~O
(8).
ТаRИМ
обраЗ0М,
для
вогнутых
МНОГОRритериальных
за
дач
справедливо
равенство
(13)

§ 2.2]
ВОГНУТЫЕ
И
ЛИНЕйНЫЕ
ЗАДАЧИ
109
ПРИ
М
е
ч
а
n
и
е
5.
Теорема
4
была
получена
нан
след
ствие
теоремы
3.
На
самом
деле,
теоремы
3
и
4
(тан
же,
нак
теоремы
1
и
2)
являются
эквивалентными.
5.
Рассмотрим
подлиппо
эффективные
оценни
и
реше
ния.
В
предыдущем
параграфе
(см.
теорему
1.16)
равен
ство
множеств
подлинно
и
собственпо
эффентивных
точен
было
установлепо
при
определенных
предположениях,
среди
ноторых
было
условие
замннутости
множества
У.
Ню<
ПОI<азывает
нпжеследующая
теорема,.
в
случае
эф
феI{ТИВНО
выпуклого
(и
не
обязательно
замннутого)
У
ра
венство
уназапных
множеств
всегда
имеет
место.
Т
е о
р
е
м
а
5.
Если
множество
У
эффе,;,тивно
выnу,;,ло,
7'0
В(У)
=
G(Y).
Д
о
н
а
з
а
т
е
л
ь
с
т
в
о.
Учитывая
теорему
1.6.1,
остает
ся
доназать
включение
В(У)
~
G(Y).
Пусть
уО
Е
В(У).
Не
умаляя
общности,
положим
уО
=
О(т).
Тан
же,
нак
и
в
доказательстве
теоремы
1.16,
предпо
лагая
противоположпое,
получим
существование
последо
вательпостей
{eh},
{уЧ
ТaIШХ,
что
Во
-+
+0
и
имеет
место
(1.22),
(1.2З).
Возможны
два
случая:
последовательность
точен
{уО}
может
оказаться
ограниченной
либо
неограни
ченноЙ.
Рассмотрим
отдельно
эти
два
случая.
1)
Пусть
sup
//
yk"
< const.
Поскольку
И3
ограниченной
k
последовательности
всегда
можно
выделить
сходящуюся
нодпоследовательность,
то
будем
считать
сходящейся
саму
последовательность:
Нm
ylt
=
у*.
И3
(1.2З)
следует
у'*::::::
k ... oo
~
О(т).
Если
у'*
=
О(т),
ТО
так
же,
как
и
в
доназательстве
теоремы
1.15,
определим
последовательность
(1.24)
и
при
дем
к
противоречию.
Пусть
у*
гО(т).
Рассмотрим
после
довательность
-/1
-/\
-k
1
/\
(J)
=<
ky
l
где
У
= k
у
t k = 1, 2,
...
-k
В
силу
выпуклости
У,*
имеем
у
Е
У
*.
Таним
образом,
-k
Нm
(J)
'=у*Е
Т
(У
*,
О(т»)'
Это вместе
снеравенством
у*
г
О(т)
противоречит
предположению
О(т)
Е!
В(
У).
2)
Пусть
sup/\ylt
11
= +
00.
Можно
считать,
что
Ily"ll:>
1,
k
k =
1,
2,...
Введем
последовательность
-h
-11
-/1
1
11
(J) = ky ,
где у
=
kll
yltll
у,
k =
11
2
!
...

110
УСЛОВИЯ
ОПТИМАЛЬНОСТИ
[гл.
2
Благодаря
выпуклости
множества
У
$
здесь
тю,же
имеем
~k
~
У
Е
У
$,
k=
1,2,
...
Последовательность
{ro
k
},
как
после~
Довательность
точек
на
единичной
заМIШУТОЙ
сфере,
мож~
НО
считать
сходящейся:
Нт
(й"
=
(й
Е
Т
(У
$,
О(m».
Ис~
пользуя
систему
неравенств
(1.23),
нетрудпо
прийти
I{
неравенству
~
;;:::
О(т),
которое
вместе
с";;;"
= 1
противоре~
ЧIlТ
предположению
О(т)
Е
В(
У).
11
Таким
образом,
в
случае
эффентивной
выпунлости
У
понятия
ПОДЛИННОЙ
и собственной
эффентивности
paBHO~
сильны.
Согласно
лемме
2
этот
вывод
справедлив,
в
част~
ности,
для
вогнутых
мпогонритериальных
задач:
если
Х
ВЫПУI\ЛО
и
/
вогнута,
то
Bj(X)
=
Gj(X)
[124].
Следователь~
но,
теоремы
3
и
4
устанавливают
таиже
характ()ристиче~
ское
свойство
подшпПIО
эффентивных
оценон
и
решений.
6.
Пусть
вогнутые
векторные
фуннции
/ =
(/1,
/2'
..•
.
..
,
/т),
g =
(gl'
g2,
...
, gk)
определены
на
выпунлом
MHO~
жестве
D
s;
Еn.
В
этом
пункте
для
задачи
с
допустимым
множеством
0.1.1)
будут
получены
необходимые
и
дo~
статочные
условия
оптимальности
в
терминах
седловых
точен
сналярной
фуннции
Лагранжа
"p(!-t,
х,
л)
=
<!-t,
/(Х»
+
<л,
g(x».
Эта
фуннция
считается
заданной
для
таних
пар
венторов
(х,
Л),
чтоХ
Е
D,
л
Е
E~;
т-мерный
вектор
!-t
здесь
яв~
ляется
парамеТРОl\I.
Напомним,
что
пара
(Х
О
,
1..0)
называется
седловой
точ~
кой
функции
Лагранжа
"p(!-t, ., .),
если неравенства
.P(~t,
Х,
1..0)
~ "p(!-t,
х
О
,
1..0)
S "p(!-t,
х
О
,
Р
(14)
имеют
место
для
всех
Х
Е
п, л
Е
E~
Т
е
о
р
е
м
а
6
Шун
-
Такнер
--Гурвич
-
Джоффри~
он).
Пусть
веroТОР-фУН1ЩUU
/, g
вогнуты
на
выnуroлом
мно
жестве
D u
выnолняеrся
условuе
регулярностu
Слейтера:
существует
таroая
rочroа
х
Е
D,
что
g(x)
>
Ощ.
Для
слабой
эффеroru·вностu
(собственной
эффеroтuвностu)
точrou
х
О
Е
Е
Х
необходимо
u
достаточно,
чтобы
существOl1алu
веro-
- k
тор
!-t
Е
М
(!-t
Е
J.\tI)
u
веroтор
1..0
Е
Е>
таroие,
что
пара
(х
О
,
1..0)
является
седЛО60Й
точroой
фунnцuu
Лагранжа.
Д
о
к
а
3
а
т е
л
ь
с
т
в
о.
Вначале
докажем
условия
Ma~
бой
эффективности.
.
