Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач
Подождите немного. Документ загружается.


§
~
!]
ОБЩИЕ
УСЛОВИЯ
ОПТИМАЛЬНОСТИ
91
в
соответствии
с
принципом
пессимизма-оптимизма
оптимальным
считается
решение,
мансимизирующее
на
Х
функцию
л
inf
\jJ
(Х
,
~t)
+
(1
-
л)
sup
\jJ
(х,
~t),
(32)
j.tEMO IlEMO
где
'л
-
некоторое
фиксированное
число
из
[О,
1].
1
Если
хеР/(Ю,
то
ф(х,
~t)=1
IIрИ~,=
f
1
(x)'
iE1If.
Наоборот,
если
ф(х',
~")
= 1
при
неI\ОТОрых
х'
Е
Х,
~t"
Е
М
О
,
то
Мх')
~
f.(x"),
i
Е
М,
где
х"
-
эффеI\тивное
jJршение,
соответствующее
~"
(см.
(25».
Поэтому
j(x')=
=
f(x"),
так
что
х'
Е
Pt{X).
Наконец,
ссли
допустить,
что
ф{х',
~"»1
при
некоторых
Х'ЕХ,
~"EMO,
то
'Jогда
должно
быть
f{x')
>
f(x")
для
эффективного
реше
IJIШ
х",
соответствующего
~",
что
невозможно.
Таким
образом,
функция
ф(х,
~)
достигает
на
М
О
своего
макси
lIума
тогда
и
только
тогда,
когда
х
Е
Pj{X).
ПОСRОЛЬRУ
из
f(x')
~
f(x")
следует
ф(х',
~)~
ф(х",~)
прп
любом
~
Е
Е;,
то
и
inf
'Ф
(х',
~t):>
inf
'Ф
(х",
~t).
I1ЕИ
О
IlEMo
Нроме
того,
согласно
теореме
3.2.4
ино;{,ество
PJ(X)
внешне
устойчиво
(см.
§ 1.4),
т.
е.
для
каждого
х"
Е
Х
найдется
такой
х'
Е
P1(X),
что
f(x')
~f(x").
С
учетом
всего
излошенного
можно
утверждать,
что
функцию
(32) I
можно
максимизировать
не
па Х,
а
па
Р/(Х).
Но
если
;r
Е
Pt{X),
то
с
учетом
(29)
эту
функцию
мошно
предста-
ппть
в
виде
л
шiп
(/1
(x)/f:)
+(1-/..).
lЕМ
Следовательно,
и
здесь
оптимальное
решепие
х*
удоn
JIстпоряет
(27)
.•
Нан
уже
УRазывалосъ
в
§
1.5,
СЧИ1'ать
оптимаЛЪНьN
решение,
обращающее
в
МЗКСIIМУМ на
Х
фуnrщию
.
\11
(Х)I
II
(х)
=
Шlll
-$-
t
1
ЕМ
/!
(33)
было
предложено
в
статье
[217],
а
затем
и
в
целом
ряде
других
работ.
Обоснование
при
этом
сводилось
R
тому,
Что
фуnrщия
(33)
безразмерна
и
ПОЗВОJшет
«равномерно»

~'СIOвия
ОПТИМАЛЬНОСТИ
[ГЛ.
2
•
по
всем
крптериям
fi
прпБШIЗИТЬСЯ
1\
их
максимумам
fi
•
Теорема
17
разъясняет
смысл
фУIШЦИИ
(33)
с
ипой
точкп
зрения
и тем
самым
открывает
новые
ВОЗМОilШОСТИ
ее
пра1\тического
использования
(пример
см.
в
[80]).
Еслп
решение,
доставляющее
фушщии
h(x)
наиболь
шее
на
Х
значение
h*,
не
еДИIlствепно, то по
мноа,естне
Х;
всех
таких
решений
могут
быть
и
но,)ффеl{ТИВIIые
решеппя.
Разумеется,
COfJlaCHO
теореме
9,
можно
найти
эффективное
решенпе
пз
Х;,
максимизируя
на
Х
ФУНН-
1n
цию
~
fi
(х)
прп
УСЛОВIШ
h(x)
= h*.
Однано,
учитывая
i=l
возможность
пееДJIнствеППОСТJI
ТОЧЮI
мансимума
Ых)
на
Х,
целесообразно
уточнить
само
определение
оптимаЛl,
ного
решения.
Действительпо,
маl\симпзация
Ых)
озна
чает
выделеппе
решений, для
ноторых
наимеиьшее
пз
значений
т
фушщий
fi
(х)/
f~
ЯВJшется
паиБОJIЬШИМ.
По
этому
далее
имеет
смысл
М1шсимизировать
на
мпоа,естпе
всех
таЮIХ
решений
второе
наимепьшее
из
значений
уна
занпых
функцнй,
затем
на
подмножестве
выделенных
пр!!
этом
решений
маНСIIмизпровать
третье
наименьшее
зна
чение
JI
т.
д.
до
т-го
наIIменьшего
(т.
е.
фю{тичеСКll
наибольшего)
из
значепиЙ.
Решения,
получающпеся
I!
результате
последовательной
маr,симизаЦIIIr
упорядочен
ных
по
возрастанию
значешrй
т
функций,
названы
в
[79)
симметрично
ленсинографичесюr
ОПТIIмальпымн,
нрашо
-
sL-оитlIмалы1вш..
Все
SL-оптимальные
реше
ния,
разумеется,
эффеI\ТПВНЫ.
Задачи
отыскания
таких
решений
иодробно
рассмотрены
в
[79, 85].
Взаимосвязь
многокритериальпых
задач
II
однонрп
териальпых
с
неопределеппыми
параметраМII
мошна
установить
11
в
других
формах,
используя
теорему
2 .
.
Так,
согласно
следствию
1
пз пее
п
прпмеру
8
выбор
единственного
(с
точностыо
до
энвивалептности
~
,)
ре
шения
из
множества
Pt(X)
раВНОСIIлен
уназанию
вен:тора
z
Е
Р(У),
который
следует
ПСПОЛЬЗ0ваТI,
прп
lI1aI,СIIмпза
ЦИИ
на
Х
фУIШЦИII
min
lfi
(х)
- Zj].
iElI1
(34)
1ft
задаче
ОПТIIмизации
с
нритерием
(34),
в
IШfОРОМ
значенпе
параметра
z
Е
Р(
У)
СЧIIтается
неп::шестньш,
тю,-

s
~,lj
ОБЩИЕ
У(;!lOВШI
ОllТI!:lI.\:lЫlUСТП
93
II,e
формально
можно
ПРIIмепить
тот
шш
ППОЙ
ПрIIlЩИП
принятия
решеrшй
в
УСЛОВIlЯХ
пеопределенности.
т
е
о
р
е
м
а
18.
Пусть
Х
-
nеnустоu
KOlftna'J'i,T
U
все
fi
uеnрерывnы.
Тогда,
согласно
nрunцunа.ч
lftaKCU.1tUna,
JltU-
HU.II.aKCnOZO
сожалеnuя
U
neCCUMU8ma-ОnТUJltU8лtа
ОnТU.llаль
иое
по
(34)
решеnuе
х*
Е
PJ(X)
удовлетворяет
условllЮ
шах
ft7
- fi
(х*)]
= min
шах
[t7
- fi
(х)].
(35)
iEM
хЕХ
iElII
Доказательство
этой
теоремы
про
водится
анаЛОГИЧIIО
доказательству
теоремы
17.
В
чаСТIIОСТИ,
шах
inf min [ti
(Х)
-
Zi]
=
тах
mш
fti
(.1')
-
f~]
=
~'eX
,еР(У)
iElI1
хеХ
iellI
=
-шil1
шах[f7
- fi
(.1')].
ХЕХ
iE1I1
Практически
определение
оптимального
решеНIIЯ,
за
даваемого
условием
(35),
можно
использовать
лишь
в
TO~[
случае,
ногда
все
нритерии
fj
однородны,
т.
е.
имеют
еди
ную
шкалу.
В
общем
же
случае
вводят
нание-либо
нор
~lПрующие
множители.
Часто
МПШIМИЗПРУЮТ
па
Х
фуrm-
цпю
(когда
все
/7>
о)
н:ти
.t;-.t;(Х)
шах.
,
iElII
f
i
-
ti~
(37)
где
в
роли
/i*
выступают,
например,
числа
mil1
fi
(х).
ХЕХ
Легко
видеть,
что
решение
х*
Е
Х
обращает
в
макси
~IYM
функцию
(36)
тогда
и
только
тогда,
Jюгда
она
удовлетворяет
равенству
(27),
ПОСRОЛЫ,У
t;-!i(Х)
(!;И)
.
!j(x)
тах
,*
=
п!ах
1 -
-,-$-
= 1 -
llllП
--*-.
,е
111
Ji
"с:\[
1;
'Е1II
fi
с
учетом
ВОЗМОiЮIOСТИ
пееДIlпствепности
точки
макси
мума
фУННЦИИ
(37)
па
Х
такте
целесообразно
искать
SL-оптимаЛЫlые
решеппп
для
задачп
l\ШШIМIlЗ3ЦI1Jl

94
условия
ОПТИМАЛЬНОСТИ
[ГЛ
2
6.
Теоремы
1
и
2
позволяют
также
дать
теоретико
игровую
интерпретацию
слабо
эффективным
и
эффектив
ным
оценкам
и
решениям.
Напомним,
что
беСI<оалициопной
игрой
двух
лиц
на
зывается
система
вида
r = <8., 82'
ер"
ер2),
где
8,
и
82-
множества
стратегий,
а
ерl
и
ер2
-
функции
выигрыша
(числовые
функции,
определенные
на
множестве
ситуа
ций
81
Х
82)
первого
и
второго
игроков
соответственно.
В
такой
игре
каждый
игрок
j
пезависпмо
от
другого
вы
бирает
свою
стратегию
8)
Е
8j.
После
того
KaI,
в
резуль
тате
выборов
образуется
ситуация
(8.,
82)~
первый
ИГРОI~
получает
выигрыш
epl(81,
82)'
а
второй
соответственно
ер2(81,
82)'
Важнейшим
принципом
оптимальности
в
бескоалп
ционных
играх
является
стремленпе
игроков
к
ситуаЦИII
равновесия
(см.
[53]):
ситуация
И1
s~)
называется
рав
новесnой,
если
ер1
(S~,
sg)
>
СР1
(81'
sg)
для
всех
81
Е
8
н
СР2
(8~,
8~)
>
СР2
И,
82)
для
всех
82
Е
82'
Если
оба этп
неравепсгва
прп
любых
S1
=F
8~,
82
=F
s~
яв
ляются строгшш,
то
(B~,
s~)
-
ситуация
строгого
равпо
веСIlЯ.
Ситуации
равновесия
(8~,
s;)
и
(s:,
8;)
назыnаются
ЭIшцвалентнJ,IМИ,
если
ер}
(8~,
8;) =
ер}
(8;,
s;),
j=1,
2.
Си
туация
равновесия
(8~,
8;)
называется
недоминируемой
(оптимальной
по
Парето),
если не
существует
ситуации
(Sl'
S2)
такой,
что
справедливы
два неравенства
СР;(8
1
,8
2
»
;;::::
ep.1-(S~'
в;),
j=
1,
2,
по
I\paiiHe~
мере
одно
из
которых
строгое.
Те
о
р
е
м
а
19.
epl,
ер2),
где
Если
У
с
Е';,
то
8
игре
r =
<У,
У,
(
)
•
Yi
%i
(Рl
У
Z =
Шlll
-,
СР2
(у,
z)
=
rnin-,
IE.1
ZJ
!ЕМ
У1
(38)

~
2 t I
ОБЩИЕ
УСПОБШI
аПТИllIАпьностrI
95
.~t1l0жество
ситуаций
равновесия
есть
{(уО,
yO)!yOeS(Y)},
а
:множество
ситуаций
строгого
равnовесия
-
{(уО,
уО)!
уО
е
Е
р(
У)},
nричеJlt
все
ситуации
равnовесия
Э/'i,вива,л,еnТllЫ
и
neaoМlmupyeJ.lbl.
Теорема
20.
В
игре
г=
<У,
У,
CPI,
СР2>,
где
!Рl
(у,
z)
=
min
(Уl
-
Z1)'
<Г2
(у,
z)
= mill
(Zl
-
У1)'
(за)
1ЕlИ
1ЕМ
;ЩlOжество
ситуаций
равновесия
еС7Ь
{(уО,
yO)!yOES(Y)},
а
Jlt1tожество
ситуаций
строгого
равновесия
_
{(уО,
уО)
I
уО
Е
Е
р(
У)},
причем
все
ситуации
равnовесия
э".вива.аеnтnы
и
neaoMunupyeJltbl.
Заметим,
что
утверждение
из
теоремы
19
о
структуре
ситуаций
равновесия
родственно
теореме
2
из
[4].
ДQказательства
теорем
19
и
20
проводятся
'аналогич~
НО,
только
в
первом
случае
используется
теорема
1,
а
во
втором
-
следствие
1.
Докажем,
например,
теорему
20.
Пусть
(уО,
ZO)
-
ситуация
равновесия:
CPI(YO,
ZO);;;::
СРl(У,
ZO)
дЛЯ
всех
у
е
У,
(40)
CP2(Y~,
ZO)
~
<Р2(УО,
z)
для
всех
z
е
У.
(41)
Из
(40),
согласно
теореме
3,
вытекает,
что
уО
Е
S(Y).
Если
же
в
(40)
при
любом
у
=1=
уО
неравенство
строгое,
TQ,
Iшк
показывает
теорема
7,
уО
Е
р(
У).
Допустим,
что
ZO
*
=F
уО.
В
силу
(40)
ZO
>
уО
невозможно
(ибо
CPl(ZO,
ZO)
=
о),
1Ю{ что
z~<y~
для
иеI{ОfОРОГО
i
Е
М.
Тогда
СР2(УО'
ZO)
<
<
о
=
СР2(УО'
уО),
что
ПРОТIIворечпт
(41).
Поэтому
ZO
=
уО.
Пусть
теперь,
наоборот,
уО
Е
S(
У).
Рассмотрим
сптуа~
цrпо
(уО,
уО).
По
следствию
1
выполняртся
(40).
ЕСЮI
II
ри
этом
уО
Е
р(
У),
то,
согласно
примеру
8,
для любого
у
=1=
уО
неравенство
(40)
будет
строгим.
Возъмем
произ
вольную
точку
z
Е
У,
отличную
от
уО.
В
силу
уО
Е
S(
У)
найдется
номер
i
Е
М,
дЛЯ
иоторого
Zl
<
y~.
Поэтому
(Р2(УО,
z):;;;
О
=
cpz(yO,
уО).
Следовательно,
выполняется
п
(41).
Если
же
уО
Е
р(
У),
то
Zj <
у.
для
не которого
i
Е
М,
11
тогда
СР2(УО,
z) <
О
=
СР2(У
О
,
уО).
Итак,
множество
ситуаций
равповесия
имеет
вид
{(уО,
yO)lyOES(Y)},
а
ситуаций
строгого
равновсспя
{(уО,
уО)!уОЕР(У)}.
ПОСIЮЛЫ{У
ср,(у,
у)
=СР2(У'
у)
=0
при
любом
у
Е
У, то
все
ситуации
равновесия
эквивалентны.
Допустим,
что
неIюторая
сптуация
равновесия
(уО,
уО)

96
~'СЛОВШI
ОПТИМАЛЬНОСТИ
(ГЛ.
2
ДОl\lинируе:\lа:
существует
сптуаЦI!J1
(У,
z)
Т[lЮ1Я,
что,
па
пример,
ср,(у,
z) >
qJl(YO,
уО)
=
О,
qJz(Y, z)
~
([2(У
О
,
уО)
=
О.
По
пз
первого
перавепства
следует
У;
> ZI,
[1
113
второго
Zi
~
УI
для
всех
i
Е
М.
Полученное
противоречие
ПОI(3ЗЫ
вает,
что
ВСЛI,ая
ситуация
равновеСIIЯ
неДОМННllруема
.•
Рассмотрим
теперь
пгру
двух
лиц
с
фикснровшlНОЙ
последовательностью
ходов
Г
1
=
«S"
S2,
qJl.
«:р2»,.ОТJIПчаю
щуюсл
от
разбиравшейся
беСI<оалицпонноп
игры
r
Te\f,
что
в
ней
первый
игрок,
пе
IIмея
ппформаЦШl
о
выборе
второго
игрока,
первым
прпнимает
решение
о
выборе
5,
Е
Е
SI
И сообщает
стратегию
81
второму
игро!,у
[22].
CJle-
довательно,
ход
второго
пгрока
состоит
в
выборе
страте
гии
82
Е
S2
из
множества
В(8,)
точек
мar,симума на
S2
его
функции
выигрыша
ЧJ2:
В
(81) = {8
2
Е
S21
«:Р2
(SI' 82) =
тах
ЧJ2
(81'
и)}.
(4.2)
UES
2
Предполагается,
что
при
любом
8,
Е
SI
мно;нество
В.(8,)
не
пусто.
Это
условие
ВЫПОJIпепо,
ногда
S2 -
компar\Т,
а
<))2(81,
82)
непрерывна
па
S2
при
каащом
8,
Е
S,.
Поскольку
выбор
второго
пгрока
первому
неизвестеп,
то
гарантированный
выпгрыш
первого
игрока,
обеспечи
В<1емый
стратегией
81,
вычисляется
по
формуле
(Р1
(81)
= illf
Ч
'
1
(SI'
S2)'
(43)
-
S'zЕН(SI)
а
наиБОJIьшпii
гарантпрованныii:
выигрыш
равеп
*
ЧJ!
=
sпр
(P1(Sl)'
slES
1
-
(44)
ОптимальноiI
для
первого
ПГjЮI:а
ЯВJIяется
стратегия
8~,
удовлетворяющая
равенству
СР1
(s:)
=
ср;,
т.
е.
обеспечива
ющая
ему
получеппе
I1аибо~ы[[('го
гарантпроваппого
вы
пгрыша.
т
е
о
р
е
м
а
21.
Пусть
У
llenYCTO,
.ЮNIтуто
и
ограnи
чети.
Тогда
в
игре
1\ =
«У,
у,
qJl,
q:'2»,
где
фуnnции
чJI
и
ЧJ2
определяются
фОР.Аtула.ItU
(39),
:Мflожество
оnти:мальnых
ст
ратегий
первого
иг
роnа
есть
Р(
У).
Т
е
о
р
е
м
а
22.
Пусть
У
-
1lеnустое,
aG.Hn1lYToe
II
ог
раНllченnое
nод.АLНQжество
Е';.
Тогда
в
игре
1\ =
«у,
У,

§ 2.2]
ВОГНУТЫЕ
И
ЛИНЕйНЫЕ
ЗАДАЧИ
97
(j)!,
(j)2»,
где
(j)t U
(j)2
определяются
фор.мула.!ftu
(38),
.мно
жество
оnтиJvtaЛЬНЫХ
стратегий
первого
игрока
есть
Р(
У).
Доказательства
обеих
этих
теорем,
первая
из
ноторых
припадлежит
Д.
А.
Молодцову
[58],
проводятся
анало
гпчным
образом.
ДOIшжем,
например,
теорему
22.
Вве-
дем
обозпачение
ЧJ2
(у)
=
тах
(j)2
(у,
z).
Тан
кан
при
любом
zEY
фIшсированном
у
Е
Ет
фуннция
(j)2(y,
z)
непрерывна
на
Ет,
то
(j):
определена
норрентно,
а
множество
В(у)
(см.
(42»
непусто,
заМIШуто
и
ограничено.
Поскольку
(j)2(Y,
у)
=
1,
то
~2(Y)
б
1
для любого
у
Е
Е
У.
Пусть
z
Е
В(у).
Тогда
для
всяного
i
Е
М
верно
Z'/Yi;;;:;
1,
отнуда
y;!Zi
~
1.
Следовательно,
(j)!(y, z)::;;
1.
lIоэтому
Возьмем
у
О
Е
Р(у).
Тогда,
согласно
теореме
1
и
при
меру
8,
(Р2(УО)
= 1
и
В(уО)
=
{уО}.
О.тсюда
вытекает,
что
-*
(j)l =
1.
Следовательно,
любая
эффеI.тивная
точна
уО
Е
У
является
оптимальной
стратегией
первого
игрона.
Пусть
теперь
уО
-
оптимальная
стратегия
первого
игрока,
Т. е.
min
(j)l
(уО,
z)
= 1.
(45)
ZEB(yO)
Допустим,
что
~2(YO)
>
1,
Т. е.
(j)2(Yo,
ZO)
> 1
при
нехото
ром
ZO
из
В(уО).
Тогда
y~/z~
> 1
при
всяхом
i
Е
М,
от
куда
(j)t(YO,
ZO)
<
1,
и
ПОJIучается
противоречие
с
(45).
Поэтому
Q;2(yO)=1
и
B(yO)={ZEYlz;;;:;yO}.
Предполо
жим,
что
в
В(уО)
найдется
ТОЧI{а
z,
отличная
от
уО.
Тогда
Zj>y~
при
не
котором
jEM,
отнуда
(j)!(yO,
z)
<
1.
А
это
Противоречит
(45).
Следовательно,
В(уО)
=
{уО}.
Это
озна
чает,
что
уО
эффективна
.•
§ 2.2.
У
словил
оптималыlстии
длл
ВОГIlУТЫХ
и
линейных
задач
В
этом
парагра.фе
равбираются
условия
оптимально
сти
для
важнейших
нлассов
многокритериальных
вадач
вогнутых
и
линейных.
Но
вначале
(п.
1)
приводятся
не-
7
в.
В.
ПОДИНОВСRИЙ,
В.
Д.
ногин

98
vсловия
ОПТИМАЛЬНОСТИ
[ГЛ.
2
обходимые
для
дальнейшего
изложения
краткие
сведения
о
вогнутых
функциях,
их
обобщениях,
а
также
об
исполь
зуемых
ниже
теоремах
об
альтернативе
для
систем
ли
нейных
и
вогнутых
неравенств.
{.
Мпожество
D s:
Еn
называется
вЫnУ""ЛЫJ,f"
если
оно
вместе
с
любыми
двумя
точками
содержит
и
соединяю
щий
их
отрезок,
т.
е.
если
(лх+
(1-
л)х')
Е
D
ПрИ
лю
бых
х,
х'
Е
D
И
л
Е
[О,
1].
Пусть
числовая
функция
h
определена
на
выпуклом
множестве
D s:
Еn.
Эту
функцию
называют
вогnутоu,
если
для
любого
л
Е
[О,
1]
и
любых
х,
х'
Е
D
ВЫПОЛЮI
ется
неравенство
h(лх
+
(1-1'')X'):>
лh(х)
+
(1-
Л)h(х').
В
том
случае,
когда
для любого
л
Е
(О,
1)
и
любых
х,
х'
Е
Е
D,
х"=
х',
имеет
место
строгое
неравенство
h(лх
+
(1-
л)х')
>
лh(х)
+
(1-
л,)h(х'),
функцию
h
называют
строго
вогnутоU.
Подробное
изложение
всевозможных
свойств
вогнутых
функций
можно
найти
в
монографии
[93].
Отметим
лишь
следующее
характеристическое
свойство
вогнутой
диф
ференцируемой
функции:
дифференцируемая
функция
h
вогнута
тогда
и
только
тогда,
l\огда
для
любых
х,
х'
Е
D
выполняется
неравенство
h(x')
-
h(x)
S
(Vh(x),
х'
-
х>.
Через
Vh(x)
здесь
обозначен
градиент
функции
h,
вы
ЧИСJIeНПЫЙ
в
точке
х.
Дифференцируемую
на
D
функцию
h
называют
псе
в-
80вотутоu,
если
для
любых
х,
х'
Е
D
неравенство
(Vh(x),
х'
-х>:5
О
влечет
h(x')
~
h(x).
Каждая
вогнутая
дифферепцируемал
функция
является
псевдовогнутой,
но
не
паоборот.
Если
для
любого
л
Е
[О,
1]
и
произвольных
х,
х'
Е
D
справедливо
неравенство
МАх
+
(1-
Л.)х')
~ min
{Ых);
h(x')},
то
фушщию
h'
называют
кваВllвогnутоU.
Кввзивогнутая
функция
h
обладает тем
свойством,
что
для
любого
числа
а
множество
{х
Е
Dlh<x)
~
а}
всегда
выпуtшо.
На
рис.
3
приведены
пллюстрации
понятий
вогну-той
(а),
псевдо-
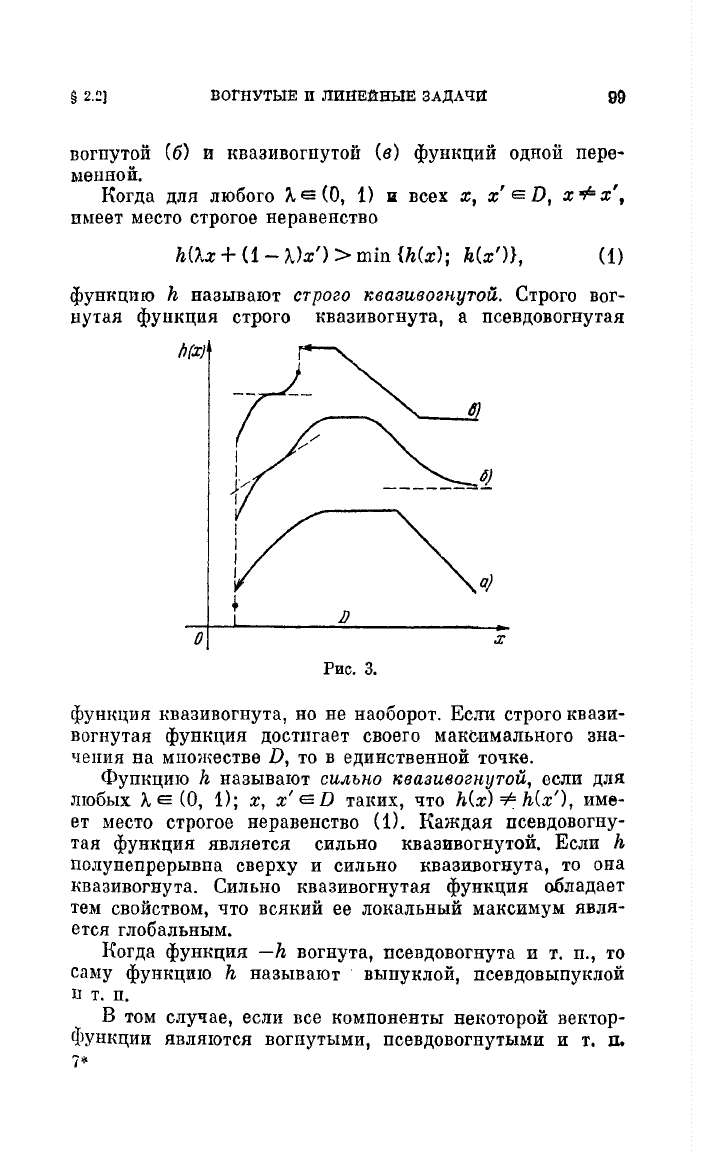
ВОГНУТЫЕ
и
ЛИIiЕЙНЫЕ
ЗАДАЧИ
99
вогпутой
(6)
и
квазивогпутой
(в)
фующий
одной
пере
менной.
Когда
для
любого
л
Е
(О,
1)
11
всех
х,
х'
Е
D,
х
+
х',
нмеет
место
строгое
неравенство
h(лх
+
(1-
,Jx')
> min
{Мх);
k(x')},
(1)
фУЮЩИЮ
h
называют
строго
~вааuвогnутоЙ.
Строго
вог
нутая
фУНКЦИЯ
строго
нвазивогнута,
а
псевдовогнутая
/J(.r)
а)
lJ
о
.:z:
Рис.
3.
фующия
нвазивогнута,
но
не
наоборот.
Если
строго
нвази
вогнутая
фующия
достпгает
своего
maHC-пмального
зна
чения
на
множестве
D,
то
в
единственной
точне.
Фушщию
h
называют
сu.лыю
-пвааuвогnутой,
если
для
любых
л
Е
(О,
1);
х,
х'
Е
D
ТaIШХ,
что
Мх)
=1=
Мх'),
име
ет
место
строгое
неравенство
(1).
Каждая
псевДОВОГНУ
тая
фуннция
является
сильно
квазивогнутоЙ.
Если
h
полунепрерывна
сверху
и
сильно
квазивогнута,
то
она
I\вазивогнута.
Сильно
нвазивогнутая
фуннция
обладает
тем
свойством,
что
всяний
ее
лональный
мансимум
явля
ется
глобальным.
Когда
фуннция
-h
вогнута,
псевдовогнута
и
т.
п.,
то
саму
фуннцию
h
называют
выпнлой,
псевдовыпунлой
II
т.
П.
В
том
случае,
если
все
номпоненты
неноторой
вентор
ФУНI\ЦИИ
Являются
вогнутыми,
псевдовогнутъши
и
т.
п.
7*

100
'УСЛОВИЯ
ОПТИМАЛЬНОСТИ
[ГЛ.
2
функциями,
эту
вектор-функцию
будем
называть
вогпу~
той,
псевдовогнутой
и
т.
п.
Некоторые
свойства
псевдовогнутых
и
квазивогнутых
функций
рассмотрены
в
книге
[37].
Подробное
изложе
ние
свойств
всех
приведенных
обобщений
вогнутой
фУНIt
ции
можно
найти
в
[197].
Важпую
роль
при
изучепии
экстремальпых
задач
иг
рают
таи
называемые
теоремы
об
альтернативе
для
си
стем
линейных
и
вогнутых
неравенств.
Насчптывается
пемалое
число
подобного
рода
теорем.
Приведем
форму
ЛИРОВRИ
некоторых
из
них.
Пусть
А
и
В
-
числовые
матрицы
размера
т
Х
n
и
k
Х
n
соответствепно.
Будем
считать,
что
матрица
А
со
держит
по
крайней
мере
один
ненулевой
элемент.
Т
е
о
р
е
м
а
(Моцюш).
И;меет
место
одиn
и
толь-по
одиn
ив
следующих
двух
случаев:
1)
систе.ма
одnородных
лиnейnых
nеравеnств
Ах>
0(111)'
Вх
~
O(k)
UJ,teeT
решение
х
Е
Еn;
2)
система
однородных
лиnейnых
уравnеnий
у
l
А
+
у
2
В
=
О(n)
имеет
решенuе
уl
>
О(т),
у2
5;;
O(k)'
Т
е
о
р
е
м
а
(Тюшер).
Имеет
место
один
и
толы'>o
один
из
следующих
двух
случаев:
1)
система
однородных
лиnейных
He.{JaeencTB
Ах
>
О(т)!
Вх
~ 0(1<)
имеет
решение
х
е
Еn;
2)
систе.~Щ
одnородпых
лиflейnых
уравnеnий
(2)
име
ет
решеnие
уl
>
О(т),
у2
~
O(k)'
Те
о
р
е
м
а
(Фан
-
Гликсберг
-
Гоффман).
Пусть
Jltno-
жество
D
~
Еn
выnу-пло
и
m-Jltерnая
веl'>ТОР-фУfll'>ция
h
вогnута
па
атом
Мflожестве.
Тогда
имеет
место
одиn и
таль-по
одиn
из
следующих
двух
случаев:
1)
систе.иа
вогnутых
1lеравеnств
h(x) >
О(т)
U.weer
ре:
шеnие
xeD;
2)
существует
тапой
веnтор
у:>
О(т),
что
<!/,
h(x»
~
~O
для
всех
xeD.
