Плетнев С.В. Магнитное поле: свойства, применение

Подождите немного. Документ загружается.

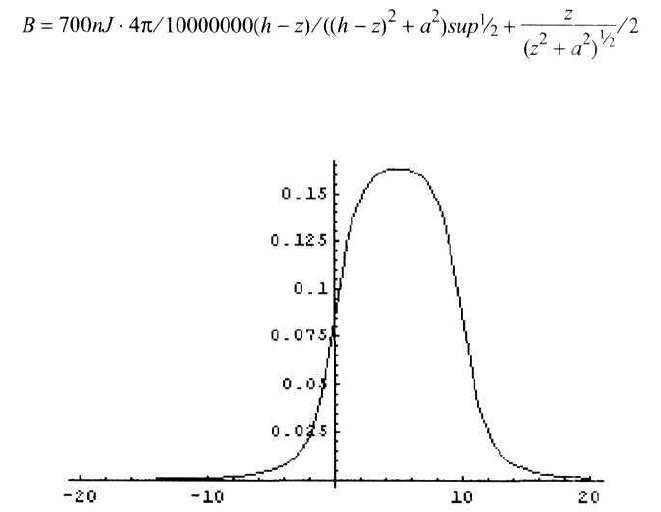
где h — это длина катушки в метрах, а — ее радиус, z — координата точки

наблюдения на оси соленоида, начиная с нижнего края катушки.

Все расчеты величин магнитных и электрических полей и вихревых токов,

а также картины пространственного распределения их векторных полей, про-

водились на компьютере в рамках прикладного пакета программ "МАТЕМА-

ТИКА 4", совместимого с операционной системой Windows98 и выше. Этот

программный продукт позволяет проводить расчеты непосредственно по фор-

мулам математической физики, в том числе решать интегро-дифференциаль-

ные уравнения, а также приводить результаты в удобном графическом виде.

В качестве конкретного примера рассчитаем зависимость величины маг-

нитной индукции B(z) в единицах тесла от расстояния z в сантиметрах по оси

соленоида до нижнего края цилиндрической катушки. Ее параметры: радиус

а=2 см, длина h=10 см, плотность витков n=100/h, ток I=0.2 ампера, магнитный

сердечник с магнитной проницаемостью μ=700. Ниже приведена соответст-

вующая расчетная формула задачи в том виде, как она непосредственно зада-

ется для компьютерного счета:

(10)

Результаты расчета удобно представить в виде графика (рис. 4.11.1):

Рис. 4.11.1 Ось ординат — расчетная магнитная индукция В в теслах по оси

катушки, ось абсцисс z — расстояние в сантиметрах от ее нижнего края.

Параметры катушки: радиус а=2 см, длина h=10 см, плотность витков

n=100/h, ток I=0.2 ампера, магнитный сердечник из феррита марки М700НН

с магнитной проницаемостью μ=700

271

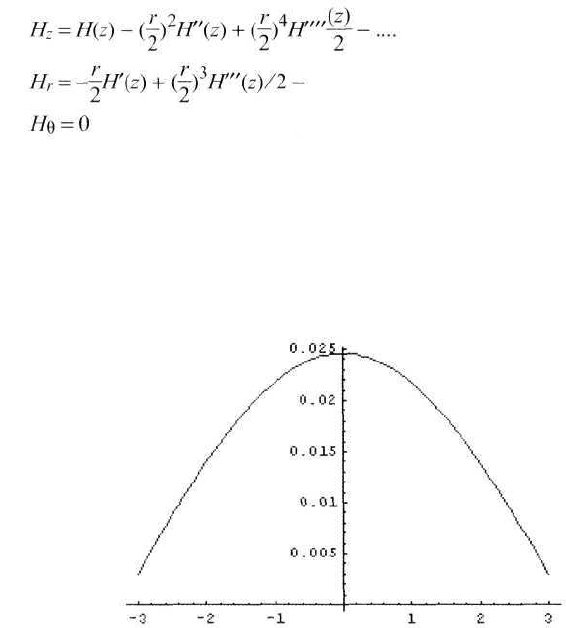
Из Рис.4.11.1. видно, что величина магнитной индукции В достигает мак-

симума B=0.17 Тл в центре катушки и плавно спадает при удалении от него.

Так, у нижнего края катушки (z=0) она уже в два раза меньше и составляет

B=0.085 Тл, а на расстоянии 2 см ниже ее края (z=-2 см) индукция равна 5=0.025

Тл =25 мТл. Предполагается, что ферритовый сердечник заполняет простран-

ство только внутри катушки, что, однако, практически не влияет на величину

магнитной индукции внутри расположенной рядом с катушкой биологической

ткани, которая имеет магнитную проницаемость μ~ 1.

Если же форма катушки отличается от цилиндрической и/или необходимо

определить магнитное поле не на ее оси, то расчетные формулы сильно услож-

няются. В таких случаях можно достаточно точно оценить соответствующие

величины, используя приближенные формулы.

В качестве примера продолжим расчет магнитной индукции цилиндричес-

кой катушки с параметрами Рис.4.11.1 в области пространства вне ее оси. Для

этого можно использовать разложение компонент магнитного поля вблизи оси

катушки по цилиндрическим координатам z и r:

(11)

С учетом выражений (8, 9) для магнитной индукции через параметры

катушки (соответствующий набор формул, вводимых для начала счета в рам-

ках пакета "МАТЕМАТИКА 4", хотя и прост, но слишком громоздок для

выписывания) получаем следующие формулы для расчета ее цилиндрических

компонент.

Для продольной компоненты Bz имеем:

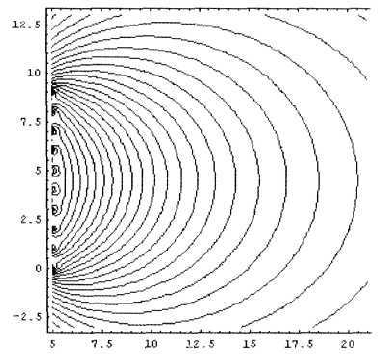
Рис.4.11.2. Расчетный график зависимости радиальной компоненты магнит-

ной индукции Вr в Тл от расстояния г в см до оси катушки с параметрами

из Рис. 1. при z=-2 см

272

Перейдем теперь к расчетам вихревых электрических полей в среде с

проводимостью X. При изменении во времени магнитной индукции B(x,y,z,t) в

области, окружающей соленоид, возникают вихревые электрические поля

E(x,y,z,t), такие, что согласно уравнению Максвелла (4):

где B

(x,y,z) — это магнитная индукция, создаваемая в пространстве вблизи

соленоида с постоянным током I

. Учитывая, что магнитная индукция может

быть представлена как ротор векторного потенциала A(x,y,z,t) [2]:

и для радиальной компоненты Вr:

(12)

(13)

Эти вихревые электрические поля вызывают соответствующие вихревые

токи в проводящей среде, где происходит изменение магнитной индукции

B(x,y,z,t).

При достаточно низкой частоте таких изменений тока I(t) в катушке

соленоида из уравнения Максвелла (3) можно с хорошей степенью точности

записать:

Из (10) и (11) получаем пропорциональность вихревого электрического

поля E(x,y,z,t) векторному потенциалу A(x,y,z,t). Поэтому, для вычисления

вихревых токов полезно провести расчет векторных полей B(x,y,z,t) и A(x,y,z,t)

для какого-нибудь постоянного тока I

, а потом этот расчёт использовать в

задаче с переменными токами низкой частоты I(t). Этому расчёту посвящено

нижеследующее рассмотрение.

В качестве начального приближения следует провести рассмотрение для

очень тонкого и длинного соленоида, так как по ряду причин оно оказывается

полезным и находит своё применение в качестве структурного элемента в

273

В приведённом примере (X,Y,Z) -- это система координат, в которой

соленоид расположен вертикально по оси Z, a (x,y,z) — это система координат,

в которой проводящие слои расположены горизонтально, т.е. перпендикуляр-

но оси z. Первые уравнения описывают преобразования компонент векторов

магнитной индукции, радиус-вектора и векторного потенциала при повороте

274

более сложных расчетах для соленоидов с большим отношением диаметра к

длине. Наличие магнитного сердечника на оси соленоида приводит лишь к

пропорциональному увеличению магнитной индукции B(x,y,z,t) во всех точках

пространства и не искажает картины силовых линий, полученной в рамках

рассмотрения простых соленоидов без сердечника.

Для бесконечно тонкого соленоида магнитная индукция в окружающем

пространстве выглядит как суперпозиция радиальных кулоновских полей от

двух разноимённых магнитных полюсов, расположенных в концевых точках

этого тонкого соленоида. Ниже показан пример применения этого подхода к

расчету величин магнитной индукции и полей векторного потенциала в про-

странстве вокруг тонкого соленоида. Соответствующий набор формул для

пакета "МАТЕМАТИКА 4" имеет следующий вид:

системы координат относительно оси у на некоторый угол от нуля до 90

градусов. Величины АХ, AY, AZ — это компоненты векторного потенциала, а

ВХ, BY, BZ — компоненты вектора магнитной индукции в той системе коорди-

нат, где соленоид зафиксирован вертикально. Величины Ах, Ay, Az и Вх, By, Bz

- это компоненты векторного потенциала и компоненты вектора магнитной

индукции, соответственно, в той системе координат, где поверхность прово-

дящей среды горизонтальна. Величина параметра а=-10 соответствует рассто-

янию в см между краями соленоида.

По теореме Стокса [2] циркуляция вектора А по аксиально-симметричной

окружности вокруг оси соленоида равна величине потока магнитной индукции

от конца соленоида через поверхность, ограниченную этой окружностью. Поэ-

тому формулы для векторного потенциала легко получаются из кулоновского

закона обратных квадратов для магнитного поля от конца длинного, тонкого,

вертикального соленоида. Это же обстоятельство упрощает метод получения

картины силовых линий магнитного поля в случае аксиальной симметрии

магнитного поля, который тогда сводится к построению линий уровня для

вспомогательной функции F{r)=A(r)r.

Действительно, для фигуры вращения, полученной при повороте силовой

линии магнитной индукции относительно оси соленоида, выполняется условие

постоянства магнитного потока через произвольное сечение. Для простейшего

случая, когда тонкий соленоид ориентирован перпендикулярно поверхности

проводящих слоёв и угол наклона, следовательно, равен нулю, картина сило-

вых линий магнитной индукции имеет следующий вид:

Рис.4.11.3. Картина силовых линий магнитной индукции вокруг тонкого

соленоида, расположенного вертикально с нижним краем в начале коорди-

нат. Расстояния по осям даны в см. Области сгущения силовых линий

соответствуют концам соленоида

275

Здесь а=10 условных единиц (например, см), а поверхность проводящих

слоев предполагается горизонтальной и проходящей через отметку 0 по высо-

те; по горизонтали отложено расстояние от оси симметрии в тех же единицах

(см).

Для получения картины распределения вихревых токов в проводящих

слоях биологических объектов удобно воспользоваться опцией Unit Step в

пакете "МАТЕМАТИКА 4", которая позволяет задавать произвольную много-

ступенчатую функцию, как сумму отдельных прямоугольных ступенек с за-

данными амплитудами и ширинами, которые соответствуют величинам про-

водимости и толщине проводящих биологических тканей, как например, на

Рис.4.11.4.:

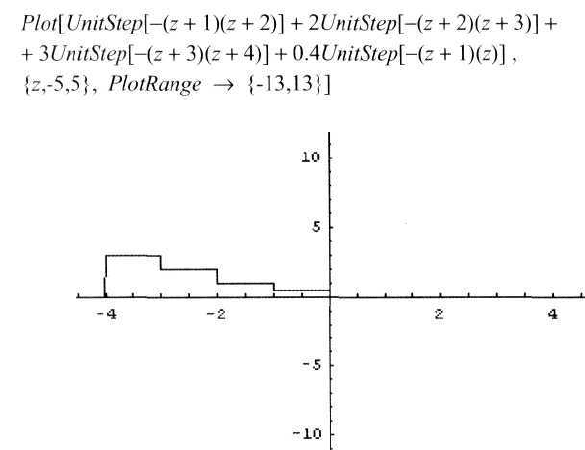
Рис.4.11.4. Здесь представлена в качестве иллюстрации модель проводящих

слоёв толщиной по 1 см с проводимостями 0.4, 1, 2 и 3 1/Ом м, соответствен-

но, для первых четырёх плоских слоев, считая от поверхности вглубь прово-

дящей среды. Ось абсцисс соответствует направлению оси соленоида

Ниже приведен расчетный график радиального распределения вихревых

токов индукции в такой модели проводящих слоёв, полученный с учётом того,

что плотность вихревых токов в некоторой точке проводящей среды пропор-

циональна величине проводимости и величине векторного потенциала в дан-

ной точке. Более светлые участки на графике Рис.4.11.5 соответствуют боль-

шим величинам плотности вихревого тока, а более тёмные — меньшим. По

вертикали z меняется от 0.1 см до 4.1 см вглубь проводящей среды. По

горизонтали отложено расстояние до оси соленоида от 0 см до 4 см:

276

Рис.4.11.5. Карта распределения амплитуды плотности вихревого тока по

глубине в слоистой проводящей среде. Ось абсцисс — расстояние от оси со-

леноида. Расстояния по осям — в см.

На некоторой глубине, скажем, z=-2, распределение плотности тока имеет

следующий вид (Из Рис.4.11.6, где изображен вид сверху на картину распре-

деления плотностей вихревых токов, следует, что плотность вихревых токов

сначала возрастает при удалении от оси соленоида, достигает максимального

значения при r~а, а затем спадает.):

Рис.4.11.6. Радиальное распределение плотности вихревого тока, созданного

переменным магнитным полем вертикально ориентированного соленоида в

отдельном слое на глубине z=-2 см

277

Если тонкий соленоид наклонён под некоторым углом к поверхности

проводящей среды, то картина распределения плотностей токов несколько

изменится. В этом случае надо писать вместо выражения для действующего

векторного потенциала другое эффективное выражение. Например, если тон-

кий соленоид расположен горизонтально и параллельно оси х и поверхности

среды, то вместо действующего векторного потенциала следует для определе-

ния установившихся вихревых токов писать выражение для эффективного

векторного потенциала АХ, AY, AZ. Оно получается, если учесть эффект ней-

трализации поперечной к поверхности среды компоненты плотности тока из-за

эффектов поляризации среды внутри проводника во внешнем, неоднородном

электрическом потенциале. Кроме того, используется тот факт, что кулонов-

ское магнитное поле от каждого конца тонкого соленоида обладает централь-

ной симметрией и подчиняется закону обратных квадратов. Тогда набор фор-

мул для пакета программ "МАТЕМАТИКА 4" приобретает вид:

Для таких случаев картина распределения плотности вихревого тока на

глубине z=-2 имеет вид:

278

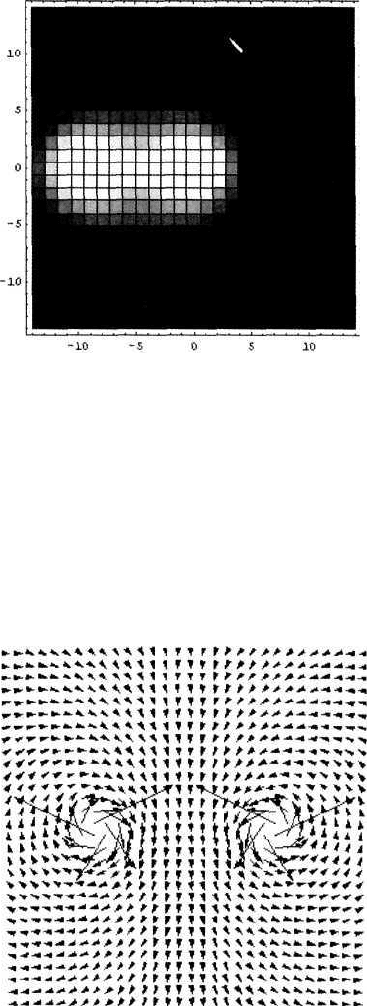
Рис.4.11.7, а. Карта распределения величины плотности вихревого тока в от-

дельном слое на глубине 2 см при горизонтальном расположении катушки

Из Рис.4.11.7, а видно, что верхний конец тонкого соленоида перемещает-

ся влево при положительных значениях параметра b — горизонтальной проек-

ции соленоида на плоскость слоя, и вправо при отрицательных. Ниже дается

картина векторного поля плотности вихревых токов на той же глубине, кото-

рая, в отличие от предыдущего рисунка, дает распределение направлений этих

токов.

Рис.4.11.7, б. Карта векторного поля плотности вихревого тока j при услови-

ях Рис.4.11.7, а. Кольцевые особенности вихревых токов соответствуют свет-

лым областям этого рисунка и расположены напротив краев соленоида

279

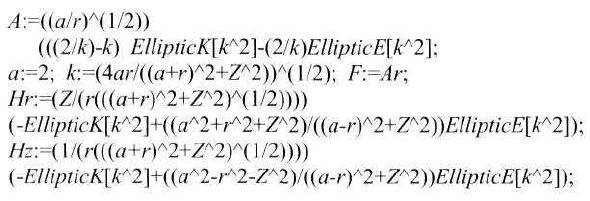
Эффект нейтрализации поперечных компонент плотностей вихревого

тока в проводящих средах возникает вследствие того, что ротор вихревого тока

пропорционален ротору действительного векторного потенциала в каждой

точке проводящей среды, то есть вектору магнитной индукции. Поскольку

кулоновское магнитное поле от конца тонкого соленоида является потенциаль-

ным, то лапласиан от вектора плотности вихревого поля обращается в ноль в

проводящей среде. Лапласиан от каждой из компонент плотности тока также

обращается в ноль. Для поперечной к поверхности проводника компоненты

плотности вихревого тока граничное условие обращения ее в ноль на этой

поверхности приводит к тривиальному решению, равному нулю во всей облас-

ти проводящей среды (в силу теоремы о существовании и единственности

решений уравнения Лапласа для гармонических функций [2]). При этом пред-

полагается, что магнитное поле меняется во времени достаточно медленно для

того, чтобы соответствующие переходные процессы релаксации успевали про-

исходить в проводящей среде. Время этой релаксации зависит от удельной

проводимости и диэлектрической проницаемости среды так, что оно уменьша-

ется при возрастании первой и убывании второй. Поэтому везде далее предпо-

лагаем, что время релаксации много меньше периода колебаний магнитного

поля. Аналогичное утверждение справедливо и для толстых соленоидов, кото-

рые в действительности могут быть представлены в виде суперпозиции доста-

точно большого числа параллельно расположенных одинаковых, тонких соле-

ноидов, так чтобы их средняя плотность в сечении толстого соленоида аппрок-

симировала магнитный поток внутри последнего. Добавляя в приведенные

выше формулы слагаемые, соответствующие этим дополнительным, тонким

соленоидам, получаем картины распределения плотностей вихревых токов для

случая произвольных толстых соленоидов, аналогичные указанным графикам,

но более размытые и светлые.

Кроме модели представления поля толстого соленоида набором парал-

лельных, тонких соленоидов, упомянутой выше, можно использовать также

аппроксимацию поля катушки в виде набора достаточно большого числа соос-

ных кольцевых витков с током, расположенных на равных расстояниях друг

от друга и имеющих одинаковый радиус. Дело в том, что магнитное поле

простого кольцевого витка и поле его векторного потенциала хорошо известно

и выражается через эллиптические интегралы Е(k) и К(k) (см., например, [2]).

Для одного витка радиуса а=2 см имеем набор формул для введения в про-

граммный пакет "МАТЕМАТИКА 4":

280