Письменный Е.Н. Теплообмен и аэродинамика пакетов поперечно-оребренных труб

Подождите немного. Документ загружается.

ГЛАВА 4

151

падения величины ψ

во всем диапазоне значений βh, не подтвер-

жденной данными глав 2, 3.

Все сказанное выше свидетельствует о том, что вопрос о влия-

нии неравномерности теплоотдачи на эффективность кольцевого

ребра требует дополнительного изучения, а известные выражения

для поправки ψ

нуждаются в совершенствовании.

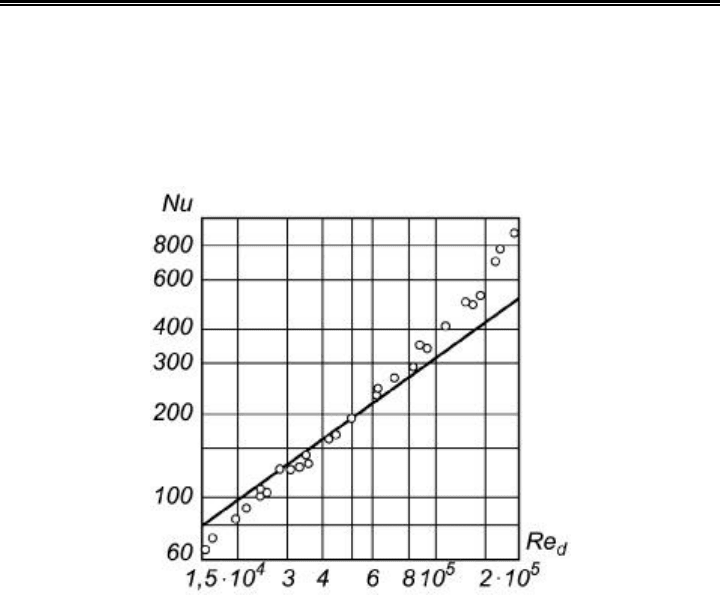
Рис. 4.27. Сопоставление опытных данных [83] (пакет 8), обработанных с по-

мощью формулы (1.21), с обобщающей зависимостью (1.23) [80] (кривая 1)

4.4.2. Результаты исследования, их анализ и обобщение

Определение величины поправки ψ

осуществлялось на основе

экспериментальных значений приведенных и конвективных коэффици-

ентов теплоотдачи тридцати двух пакетов труб серий 7 - 9, 12 и рассчи-

танных по соотношению (4.7) с учетом теплоотдачи торцов ребер зна-

чений коэффициента теоретической эффективности ребра Ε. При этом

использовалось соотношение (1.22). На рис. 4.28 опытные значения ψ

по аналогии с работами [81, 122] представлены в виде зависимости от

параметра βh. Здесь же штриховой линией нанесена расчетная зависи-

мость (1.21) из работы [81]. Из рисунка видно, что характер изменения

в области βh < 1,1...1,3 в целом соответствует данным [81, 122] - по-

правка ψ

с ростом βh уменьшается. Однако при βh > 1,1...1,3 характер

зависимости ψ

от βh изменяется: ψ

во всех рассмотренных случаях

становится практически постоянной величиной, зависящей от геомет-

рии ребра и в гораздо меньшей степени от геометрии размещения труб

в пакете. Эти закономерности достаточно хорошо объясняются резуль-

татами исследований течения и локальной теплоотдачи, полученными

в настоящей работе (гл. 2, 3), а также данными работ [8, 121], если

учесть, что при фиксированной геометрии и теплопроводности ребер

изменение параметра βh определяется изменением числа Рейнольдса.

Раздел 4.5

152

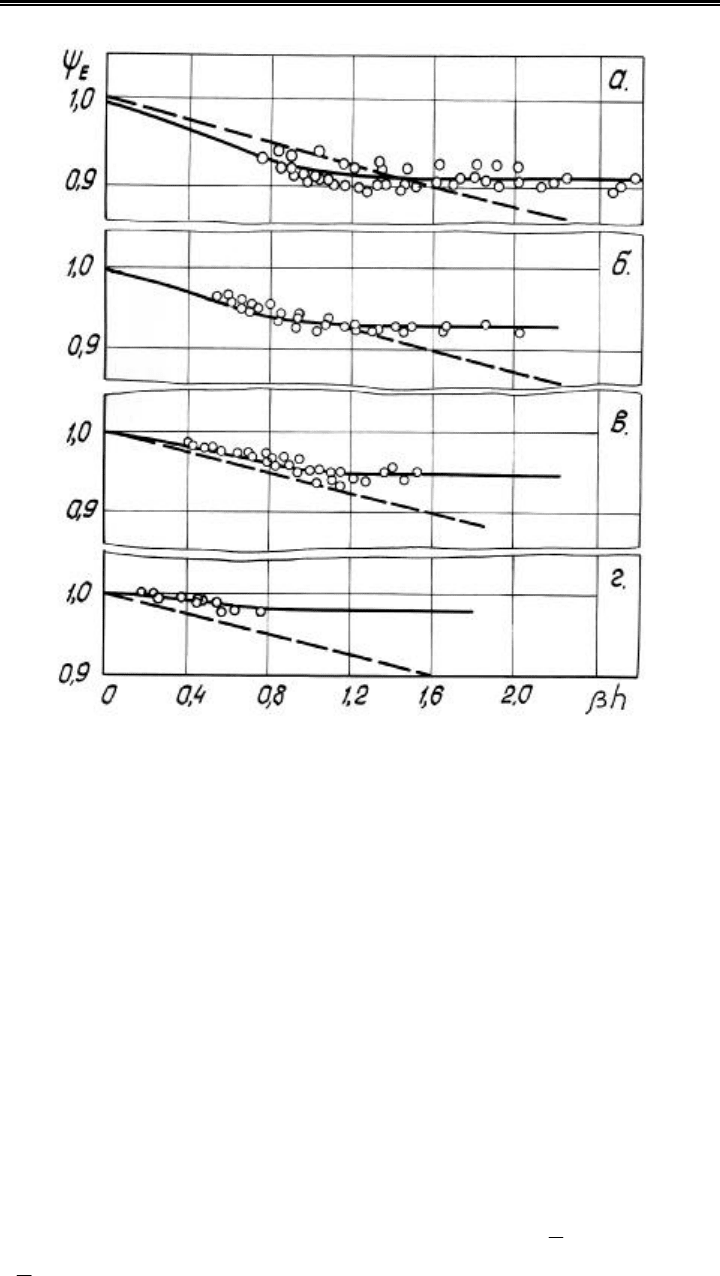
Рис. 4.28. Зависимости ψ

= f (βh) : a – D/d = 3,86; б – D/d = 3,29; в – D/d = 2,71;

г – D/d = 1,69. Перерывистые прямые – зависимость (1.21) [81]

Область малых значений βh (0,1...1,3) соответствует числам

Рейнольдса, относящимся к режиму преимущественно ламинарного

обтекания ребристой трубы, при котором интенсивность вторичных

циркуляционных течений у основания ребра невелика и распределе-

ние коэффициентов теплоотдачи по высоте ребра отвечает традици-

онным представлениям: a на внутренних прикорневых участках

ребра значительно ниже, чем на внешних, прилегающих к его кром-

ке. Если отвод теплоты от "холодных" внешних участков ребра бо-

лее интенсивный, чем от "горячих" внутренних, то перепад темпера-

тур по его высоте выше, а эффективность соответственно ниже

значений, определенных при условии a = const. Поправка ψ

в этом

случае меньше единицы. Повышение общего уровня теплоотдачи,

которое имеет место при росте числа Рейнольдса (а значит и βh)

приводит в рассматриваемой режимной области к дальнейшему

снижению эффективности ребра даже при сохранении постоянства

соотношения уровней теплоотдачи прикорневых

(

α )

и внешних

(

α )

участков ребра, что соответствует выводам работы [121].

ГЛАВА 4

153

Изменение характера зависимости ψ

= f(βh) в области

βh > 1,1...1,3 связано с переходом к режиму преимущественно тур-

булентного обтекания ребристой трубы, сопровождающимся обра-

зованием утолщенного пограничного слоя, значительной интенси-

фикацией вторичных циркуляционных течений и существенным

повышением теплоотдачи у основания ребра. При этом с ростом

числа Рейнольдса (и, следовательно, βh), судя по результатам теоре-

тического анализа [121] и данным по локальному теплообмену, со-

отношение

α / α

постепенно растет, оставаясь в то же время

меньше единицы, вследствие чего и поправка ψ

сохраняет значения,

меньше единицы.

Обращает на себя внимание и то, что по мере снижения пара-

метра D/d значение, на котором стабилизируется поправка ψ

воз-

растает. Отмеченный факт согласуется с выводами работ [123, 124]

в отношении значимости величины D/d и находится в хорошем

соответствии с выводами глав 2, 3 о том, что с уменьшением отно-

сительной высоты ребра доля его прикорневой поверхности, под-

верженной воздействию интенсивных вторичных течений, увели-

чивается, а это в итоге приводит к росту соотношения

α / α

следовательно ψ

Расслоение опытных данных, связанное с влиянием на величи-

ну ψ

геометрии размещения труб в пакетах наблюдается только при

самом большом из исследованных значении относительной высоты

ребра (D/d = 3,86), когда имеет место наибольшая степень вытесне-

ния потока из межреберных каналов вследствие нарастания толщи-

ны пограничного слоя на ребре. Однако даже в этом случае влияние

характеристик размещения на величину ψ

весьма мало - связанный

с ним рассев опытных точек сопоставим с рассевом, обусловленным

погрешностью экспериментов. В связи с этим включение параметров

размещения труб в пакетах в зависимость для определения поправки

представляется нецелесообразным, тем более, что значение

D/d = 3,86 заметно отличается от значений D/d, характерных для ис-

пользуемых на практике оребренных труб (D/d » 1,5...1,9).

Принимая во внимание сказанное выше, а также данные работ

[81, 121-124], можно сделать вывод, что формулу для расчета по-

правки ψ

следует искать в виде:

= f(D/d; Re; βh).

Однако выполненный регрессионный анализ показал, что при вклю-

чении в регрессию параметра βh полностью отпадает необходимость

включения в нее числа Рейнольдса. Сделанный вывод совпадает с

соображениями, высказанными по этому поводу в работе [81] и яв-

ляется вполне закономерным с учетом сказанного выше о зависимо-

сти βh от Re.

Раздел 4.5

154

Обработка данных дала в итоге следующую зависимость для

расчета ψ

[ ]

ψ 10,01611 + th(2βh 1)

æö

=---

ç÷

èø

. (4.56)

Зависимость (4.56) отражает асимптотическое стремление величины

к постоянному значению при D/d = const и βh ® ¥ , а также ее

стремление к единице при D/d ® 1 и βh ® 0. Расчет величины по-

правки с помощью выражения (4.56) показал хорошее согласование

с экспериментальными данными, что видно из рис. 4.28, на котором

расчетные кривые нанесены сплошными линиями.

4.5. Обобщенная методика расчета теплообмена

пакетов поперечно-оребренных труб. Сравнение с обоб-

щениями других авторов

Сопоставление формул для расчета теплообмена шахматных

(4.30), (4.32) и коридорных (4.43), (4.47) пакетов ребристых труб по-

казывает, что они имеют одинаковую структуру. Различие заключа-

ется только в определении аргумента функции thX, получившего на-

звание параметра формы пакета X.

Таким образом, получена единая система обобщающих соот-

ношений, позволяющих в интервале чисел Рейнольдса

Re = 5×10

...2×10

рассчитывать значения коэффициентов теплоотда-

чи как шахматных, так и коридорных пакетов поперечно-

оребренных труб со степенью оребрения ψ = 1,2...39,0, относитель-

ными поперечными и продольными шагами, лежащими соответст-

венно в интервалах s

= 1,7...6,5, s

= 1,3...9,5 (s

= 0,3...5,2):

Nu = 1,13 C

Pг

0,33

; (4.57)

m = 0,7 + 0,08 thX + 0,005 ψ ; (4.58)

(

)

1,1

C(1,36thX)0,014

ψ+8

=--

, (4.59)

где параметр формы пакета X, учитывающий особенности его ком-

поновки, определяется в случае шахматного расположения труб по

формуле

1,26

X = 2

σψ

, (4.60)

ГЛАВА 4

155

а в случае коридорного -

X = 42 +

æö

ç÷

èø

. (4.61)

Коэффициент С

, учитывающий влияние на теплообмен числа попе-

речных рядов труб z

, для шахматных пакетов, имеющих s

³ 2 и

< 8, а также для коридорных пакетов при любом s

и 2 £ z

< 8

определяется с помощью соотношения

0,03

C3,5z2,72

; (4.62)

для шахматных пакетов при s

< 2 и z

< 8 расчет следует произ-

водить по формуле

0,05

C3,15z2,5

. (4.63)

Если число рядов труб z

³ 8, то следует принимать С

= 1,0.

Физические константы в числах подобия относятся к средней

температуре газов в пакете, скорость - к наиболее узкому его сече-

нию (поперечному или диагональному).

При переходе от конвективных к приведенным коэффициентам

теплоотдачи (и наоборот), осуществляемом с помощью известного

соотношения (1.22), предлагается использовать упрощенное выраже-

ние для расчета коэффициента теоретической эффективности ребра

E = th(bh

)/bh

, (4.64)

в котором

δ DD

hh + 10,1910,054n

2dd

éù

æöæö

=++

ç÷ç÷

êú

èøèø

ëû

, (4.65)

что справедливо при D/d £ 3 и βh £ 2, а также асимптотическое соот-

ношение для определения поправки ψ

, учитывающей влияние нерав-

номерности теплоотдачи поверхности ребра на его эффективность

ψ 10,01611th(2βh 1)

æö

éù

=--+

ç÷

ëû

èø

, (4.66)

границы применимости которого составляют: D/d = 1,1...4,0;

bh = 0,1…3,0.

Система обобщающих соотношений (4.57) - (4.66) обеспечива-

ет более высокую точность расчета теплообмена пакетов поперечно-

оребренных труб по сравнению с другими, имеющимися на

Раздел 4.5

156

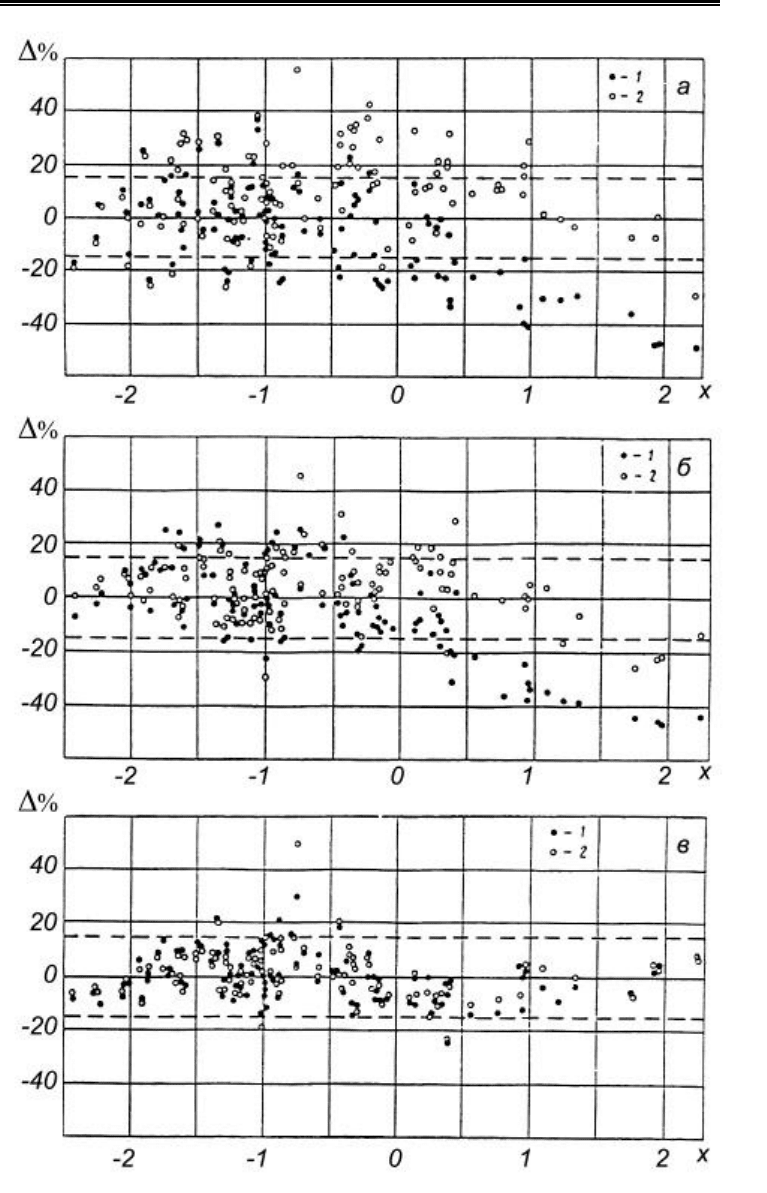
Рис. 4.29. Сравнение точности методик расчета теплообмена шахматных паке-

тов ребристых труб: а – нормативная зависимость [77]; б – зависимости ЦКТИ

[36]; в – зависимости (4.57) – (4.60). 1 – Re = 5000; 2 – Re = 60000

ГЛАВА 4

157

сегодняшний день расчетными методиками [17, 36, 77, 94, 95, 98] в

значительно более широком диапазоне геометрических характеристик

при использовании в числах подобия Nu и Re простого определяющего

размера - диаметра несущей трубы d. Это подтверждается результа-

тами сравнительной оценки точности методик, выполненной авто-

ром [91, 125] по опубликованным данным исследований 120 вариан-

тов пакетов оребренных труб с шахматной и 60 вариантов с

коридорной компоновкой, полученным методом полного теплового

моделирования (табл. 4.10, 4.11, рис. 4.29, 4.30), а также результата-

ми анализа, выполненного независимо в ВТИ и ЦКТИ [126] для 122

вариантов пакетов с шахматной компоновкой (рис. 4.31). В таблицах

4.10, 4.11, обобщающих итоги сопоставления, для каждой из рас-

смотренных методик приведено выраженное в процентах количество

пакетов, теплоотдача которых описывается соответствующими фор-

мулами с погрешностью, не превышающей заданного значения Δ

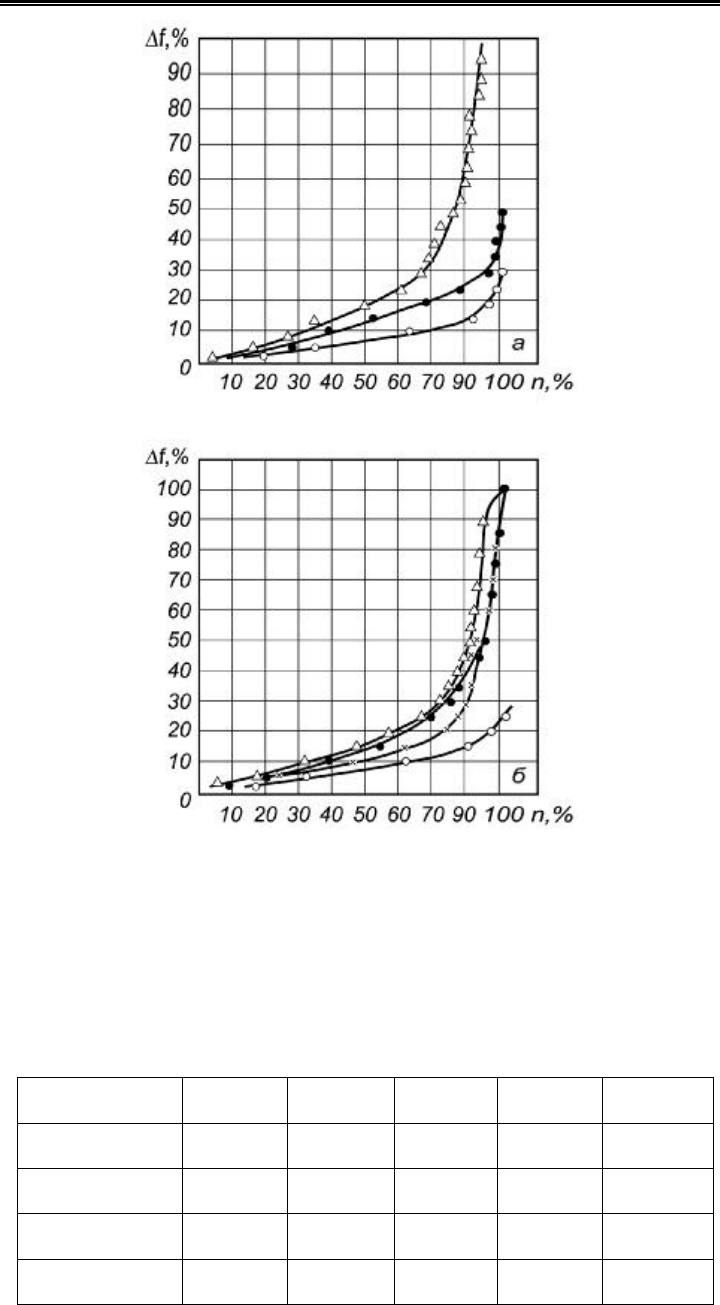
На рис. 4.31 по оси абсцисc отложена в процентах доля опытных

данных, отклонение которых от расчета не превышает значения мо-

дуля, отложенного по оси ординат.

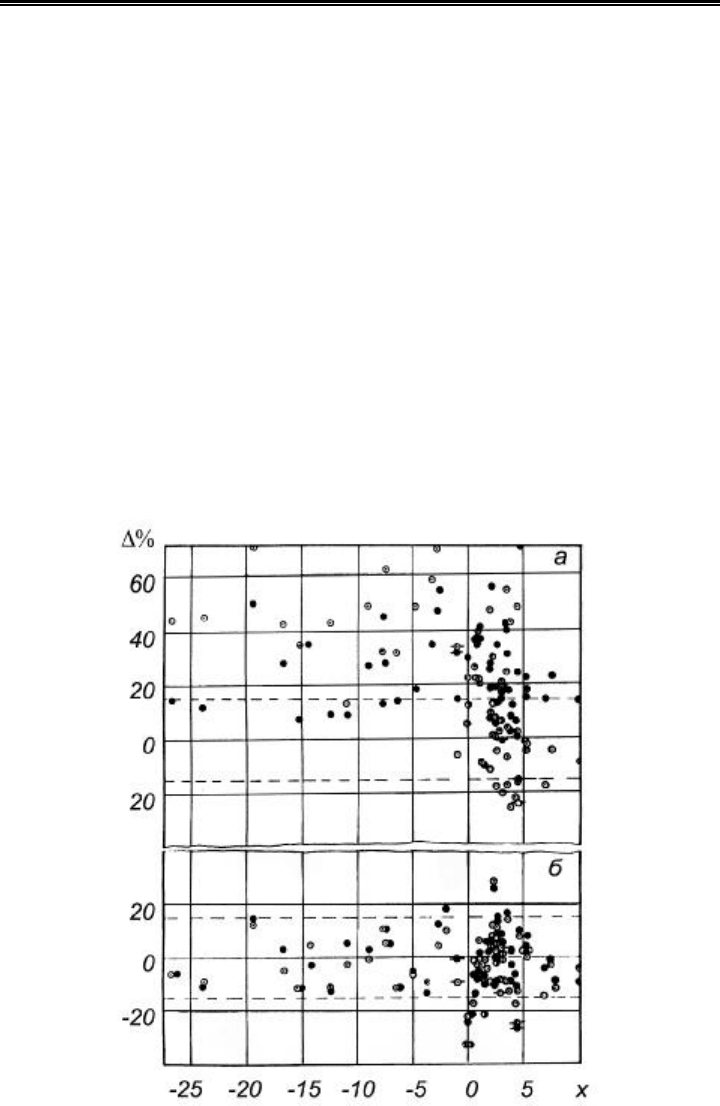
Рис. 4.30. Сравнение точности методик расчета теплообмена коридорных пакетов

ребристых труб: а – зависимость ЦКТИ [36]; б – зависимости (4.57) – (4.59),

(4.61) (точки со светлым фоном соответствуют Re = 5000; с темным – Re = 70000)

____________________

Результаты сопоставления с методиками [94, 95, 98], полученными в отно-

сительно узких интервалах геометрических и режимных характеристик, в итого-

вые таблицы не включены.

Раздел 4.5

158

Рис. 4.31. Распределение отклонений величин коэффициентов теплоотдачи, рас-

считанных по методике, предлагаемой в настоящей работе, а также по наиболее

известным методикам [77, 36, 17], от опытных значений для шахматных пакетов

поперечно-оребренных труб [126]: а – Re = 60000; б – Re = 10000. = – по [77];

Ð – по [36]; r – по [17]; ¡ – по формулам (4.57) – (4.60)

Таблица 4.10

Результаты сопоставления методик расчета теплообмена

шахматных пакетов поперечно-оребренных труб

D £ ±10% D £ ±15% D £ ±20% D £ ±30% D £ ±50%

ВТИ-ЦКТИ [77] 29,6 42,6 57,4 80,9 99,1

ЦКТИ [36] 41,7 60,9 79,1 88,7 100,0

ИФТПЭ АН

Литвы [17]

12,2 22,6 47,8 77,4 97,4

КПИ 74,8 93,9 96,5 99,1 100,0

ГЛАВА 4

159

Таблица 4.11

Результаты сопоставления методик расчета теплообмена

коридорных пакетов поперечно-оребренных труб

D £ ±15% D £ ±20% D £ ±30% D £ ±40% D £ ±50%

ВТИ-ЦКТИ [77] 36,7 50,0 83,3 95,0 100,0

ЦКТИ [36] 20,0 40,0 53,3 71,6 85,0

КПИ 85,0 88,3 96,6 98,3 100,0

Рис. 4.32. Виды ребристых поверхностей, теплообмен которых описывается

расчетными соотношениями (4.57) – (4.63): а – трубы с винтовым оребрением;

б – трубы с квадратными ребрами; в – поверхности с лепестковым оребрением.

Кроме того, расчетные зависимости (4.57)-(4.61) в отличие от зави-

симостей других авторов описывают предельные случаи, когда ни-

велируются различия между шахматной и коридорной компоновка-

ми оребренных труб (см. раздел 4.2.2), а также достаточно точно

обобщают экспериментальные данные по теплоотдаче и таких видов

поперечно-оребренных поверхностей, как пакеты труб с квадрат-

ным, и прямоугольным лепестковым оребрением [I27] (рис. 4.32).

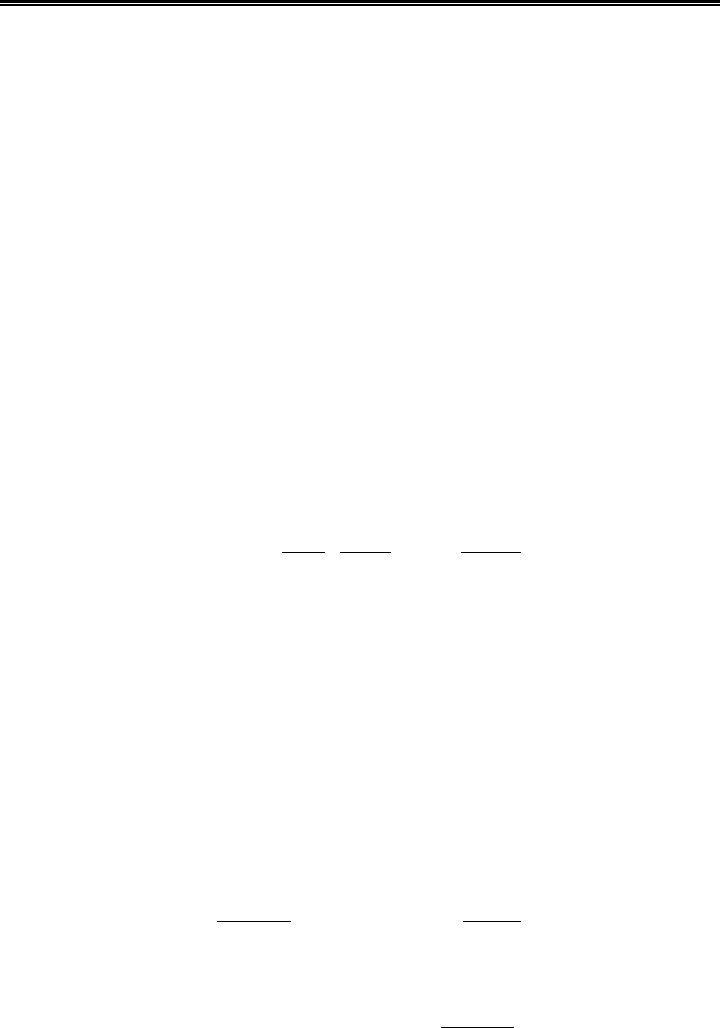
ГЛАВА 5

160

5. АЭРОДИНАМИЧЕСКОЕ СОПРОТИВЛЕНИЕ

ПАКЕТОВ ПОПЕРЕЧНО-ОРЕБРЕННЫХ ТРУБ

5.1. Методика исследований

Аэродинамическое сопротивление пакетов поперечно-

оребренных труб, геометрические характеристики которых пред-

ставлены в таблицах 4.1, Π.1 - П.7, исследовалось в условиях изо-

термического течения при температурах воздуха Т

= 293...300 К.

Определение потерь давления осуществлялось по разности статиче-

ских давлений до и после пакета поочередно на одно-, двух-, трех-,

четырехрядных и т.д. компоновках с учетом потерь на трение в про-

точной части стенда, а в случае установки в рабочем участке профи-

лированных вставок и с учетом местных сопротивлений сужения и

расширения канала

ут

сттм

эт

ρU

P = P ξ

d22

æö

DD-×+×

ç÷

èø

(5.1)

В этом выражении ΔP

cт

- измеренный перепад давлений;

ΔΡ

- дли-

на участка между точками измерения давления за вычетом глубины

исследуемого пакета; d

эт

- гидравлический диаметр прямого неза-

громожденного канала проточной части; U

- скорость воздуха в не-

загроможденных участках канала; U

ут

– скорость воздуха в сужен-

ном вставками участке канала; x

= 0,13 - суммарный коэффициент

местных сопротивлений сужения и расширения канала; l

- коэф-

фициент сопротивления трения, определяемый в соответствии с [90]

по формулам:

при

тэт

этт

эт

Ud64

Re310

ν Re

=<×= ; (5.2)

при Re

эт

> 3×10

0,25

эт

0,316

= . (5.3)

По значениям ΔΡ определялись числа Эйлера для пакета в целом

Eu = DP/rU

(5.4)

и числа Эйлера, отнесенные к одному поперечному ряду

= Eu/z

. (5.5)