Пирс Б. Типы в языках программирования

Подождите немного. Документ загружается.

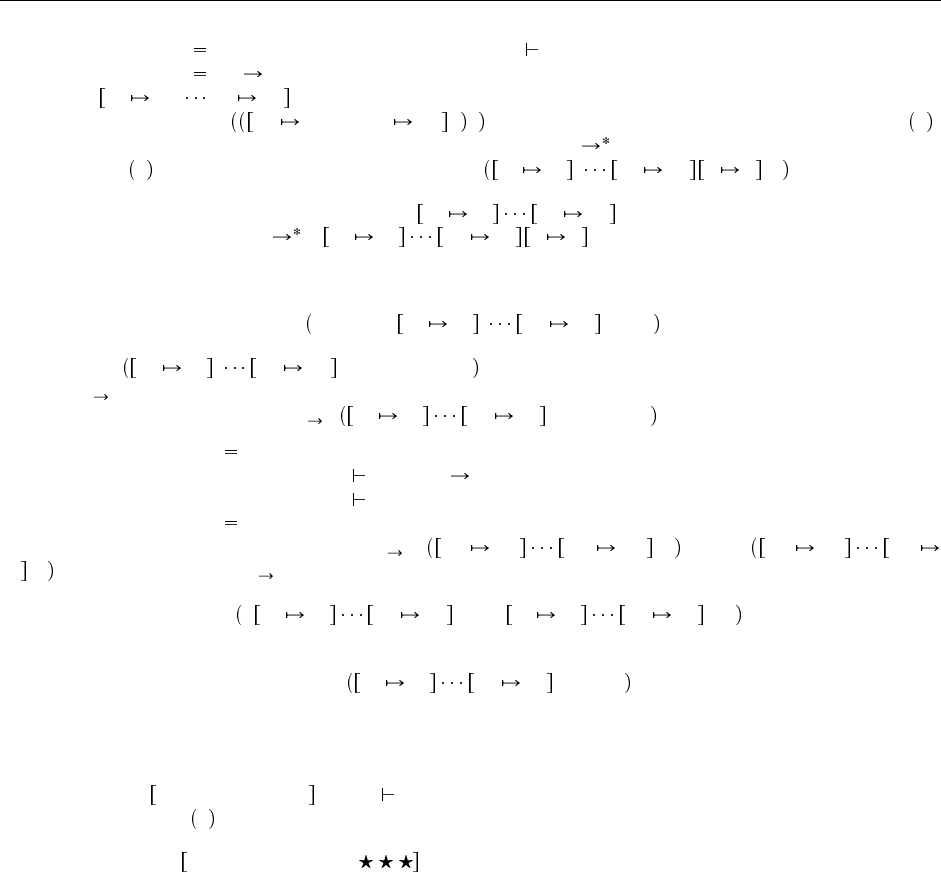
12.2. Дополнительные замечания 121

Вариант T-Abs: t λx:S

, . . . , x

, x:S

: S

T S

Очевидно, x

, x

t дает при вычислении значение, поскольку это уже значение. Оста-

ется показать, что R

, . . . x

t s для всякого терма s : S

, такого, что R

s .

Допустим, s — такой терм. Согласно Лемме 12.1.3, имеем s v для некоторого v. Согласно Лем-

ме 12.1.4, R

v . По предположению индукции, R

, x

x v s

. Однако

(λx:S

. x

) s

x v s

и отсюда по Лемме 12.1.4

(λx:S

. x

, x

) s ,

то есть, R

, x

(λx:S

. s

) s . Поскольку s был выбран произвольно, по опреде-

лению R

, имеем

(λx:S

) .

Вариант T-App: t t

, . . . x

: T

, . . . x

: T

T T

Предположение индукции дает нам R

и R

. По определению R

( x

) ( x

)

т. е.,

)

Теперь можно получить свойство нормализации как простое следствие, если считать, что терм t в

Лемме 12.1.5 замкнут, и затем использовать то, что все элементы R

нормализуемы для всякого T.

Теорема 12.1.6 Нормализация : Если t : T, то t нормализуем.

Доказательство: R

t по Лемме 12.1.5; следовательно, t нормализуем по Лемме 12.1.3.

Упражнение 12.1.7 Рекомендуется, : С помощью методов этой главы покажите, что про-

стое типизированное лямбда-исчисление сохраняет свойство нормализации, будучи расширено булев-

скими значениями (Рис. 3.1) и типами-произведениями (Рис. 11.5).

12.2. Дополнительные замечания

В теоретической литературе свойство нормализации обычно формулируется как строгая нормализа-

ция для исчислений с полной (недетерминистской) бета-редукцией. Стандартный метод доказательства

был изобретен Тейтом (Tait 1967); Жирар обобщил его на Систему F (Girard 1972, 1989); затем Тейт

упростил доказательство (Tait 1975). В этой книге мы адаптируем метод Тейта для вызова по значению,

как это сделал Мартин Хофман (личное сообщение). Классическая литература по методу логических

отношений включают работы Ховарда (Howard 1973), Тейта (Tait 1967), Фридмана (Friedman 1975),

Плоткина (Plotkin 1973, 1980) и Стэтмана (Statman 1982, 1985a, 1985b). Этот метод также описывается

во многих работах по семантике, например, в книгах Митчелла (Mitchell 1996) и Гантера (Gunter 1992).

Доказательство строгой нормализации по Тейту в точности соответствует алгоритму вычисления

термов с простой типизацией, известному как нормализация вычислением или частичное вычисление,

управляемое типами (Berger 1993; Danvy 1998); см. также работы Бергера и Швихтенберга (Berger

and Schwichtenberg 1991), Филински (Filinski 1999, 2001) и Рейнольдса (Reynolds 1998a).

rev. 104

122 12.2. Дополнительные замечания

rev. 104

Глава 13

Ссылки

До этого момента мы рассмотрели некоторое количество чистых языковых конструкций, включая

функциональную абстракцию, базовые типы вроде чисел и булевских значений, и структурированные

типы вроде записей и вариантных типов. Эти конструкции составляют скелет большинства языков

программирования, включая чисто функциональные, такие, как Haskell, «функциональные по большей

части», такие, как ML, императивные вроде C и объектно-ориентированные вроде Java.

В большинстве практических языков программирования имеются также различные грязные кон-

струкции, которые невозможно описать в рамках простой семантической модели, используемой нами

до сих пор. В частности, помимо порождения результатов, вычисление термов в этих языках может

приводить к присваиванию значений изменяемым переменным (ячейкам по ссылке, массивам, изменяе-

мым полям записей, и т. п.); вводу и выводу в файлы, на дисплеи, по сетевым соединениям; нелокальной

передаче управления через исключения, переходы или продолжения; синхронизации и обмену инфор-

мацией между процессами, и так далее. В литературе по языкам программирования такие «побочные

эффекты» вычисления обычно называют вычислительными эффектами.

В этой главе мы увидим как одна из разновидностей вычислительных эффектов — изменяемые

ссылки, — может быть добавлена в изучаемые нами исчисления. Основная добавка будет заключаться

в явных операциях с памятью (или кучей). Это расширение нетрудно определить; самое интересное

начнется, когда возникнет необходимость уточнить теорему о сохранении типов (13.5.3). Еще один вид

эффектов — исключения и нелокальную передачу управления, — мы рассмотрим в Главе 14.

13.1. Введение

Почти все языки программирования

обладают в каком-то виде операцией присваивания, изменя-

ющей содержимое заранее выделенного куска памяти. В некоторых языках, — в частности, в ML и

родственных ему, — механизмы связывания имен и присваивания разделены. Можно иметь перемен-

ную x, чьим значением является число 5, а можно иметь переменную y, чьим значением является

ссылка (или указатель) на изменяемую ячейку с текущим содержимым 5, и программисту видно это

различие. Можно сложить x с другим числом, но не присвоить ему новое значение. Переменную y

можно напрямую использовать для присваивания нового значения ячейке, куда она указывает (это

записывается y:=84), но нельзя ее прямо употребить как аргумент plus. Для этой цели требуется явно

разыменовать ссылку, написав !y для обращения к ее текущему содержимому. В большинстве других

языков — в частности, во всех членах семейства C, включая Java, — каждое имя переменной называет

изменяемую ячейку, и операция разыменования переменной с целью получения ее текущего значения

производится неявно.

В этой главе рассматривается простое типизированное лямбда-исчисление с типом Unit и ссылками (Рис. 13.1).

Соответствующий интерпретатор на OCaml называется fullref.

Даже «чисто функциональные» языки, такие как Haskell, через расширения вроде монад.

Строго говоря, правильнее рассматривать большинство переменных типа T в C или Java как указатели на ячейки,

содержащие значения типа Option(T), поскольку содержимым переменной может быть либо обыкновенное значение, либо

особое значение null.

123

124 13.1. Введение

С точки зрения формального исследования полезно разделять эти механизмы;

наше описание в

этой главе будет близко следовать модели ML. Уроки этого описания легко можно перенести на язы-

ки семейства C, если забыть некоторые различия и сделать кое-какие операции, вроде обращения по

ссылке, неявными.

13.1.1. Основные понятия

Основные операции над ссылками – выделение памяти, разыменование и присваивание. Чтобы

выделить память для ссылки, используется оператор ref, и ему в качестве аргумента дается начальное

значение новой ячейки.

r = ref 5;

r : Ref Nat

Ответ программы проверки типов указывает, что значением r является ссылка на ячейку, которая

всегда будет содержать число. Чтобы считать текущее значение этой ячейки, мы используем оператор

разыменования !.

!r;

5 : Nat

Чтобы изменить значение, содержащееся в ячейке, используется оператор присваивания.

r := 7;

unit : Unit

(Результатом присваивания служит вырожденное значение unit; см. 11.2.) Если мы снова разыменуем

r, получим обновленное значение.

!r;

7 : Nat

13.1.2. Побочные эффекты и последовательность действий

То, что результатом выражения присваивания является вырожденное значение unit, хорошо соче-

тается с нотацией последовательного исполнения, определенной в $11.3, которая позволяет нам писать

(r := succ (! r ); !r );

8 : Nat

вместо эквивалентного, но более громоздкого

(λ_ : Unit . !r) (r := succ (! r ));

9 : Nat

с целью выполнить по порядку два выражения и вернуть значение второго. Требование, чтобы тип

первого выражения был Unit, помогает программе проверки типов выловить некоторые глупые ошибки:

первое значение разрешается отбросить, только если оно и вправду с гарантией вырождено.

Заметим, что, если второе выражение также является присваиванием, то тип всей последователь-

ности опять будет Unit, мы имеем право опять использовать его на левой стороне ; и построить еще

более длинную цепочку присваиваний:

(r := succ (! r ); r := succ (! r ); r := succ (! r ); r := succ (! r ); !r );

13 : Nat

Можно также построить аргумент в пользу того, что такое разделение благотворно и с точки зрения проектирования

языков. Когда использование изменяемых ячеек памяти оказывается явной операцией, а не умолчанием, это стимули-

рует функциональный по большей части стиль программиования, где ссылки используются относительно редко; такая

практика приводит к программам, которые намного легче писать, поддерживать и исследовать, особенно если в языке

есть конструкции вроде параллелизма.

rev. 104

13.1. Введение 125

13.1.3. Ссылки и псевдонимы

Необходимо помнить о различии между ссылкой, связанной с переменной r, и ячейкой памяти, на

которую указывает эта ссылка.



Если мы сделаем копию r, например, связав ее значение с другой переменной, s:

s = r ;

s : Ref Nat

скопируется только ссылка (стрелка на диаграмме), а не ячейка:







Можно это проверить, присвоив новое значение s

s := 82;

unit : Unit

и считав его через r:

!r;

82 : Nat

Ссылки r и s называются псевдонимами одной и той же ячейки.

Упражнение 13.1.1 : Нарисуйте подобную диаграмму, показывающую результат выполнения вы-

ражений a = {ref 0, ref 0} и b = (λx:Ref Nat. {x,x}) (ref 0)).

13.1.4. Разделяемое состояние

Возможность наличия псевдонимов сильно усложняет рассуждения о программах, использующих

ссылки. Например, выражение (r:=1;r:=!s), присваивающее 1 переменной r, а затем немедленно за-

тирающее это значение текущим значением переменной s, работает точно так же, как простое присва-

ивание r:=!s, за исключением ситуации, когда r и s являются ссылками на одну и ту же ячейку.

Разумеется, в то же время псевдонимы — одно из основных полезных свойств ссылок. В частности,

они позволяют организовывать «неявные каналы связи» — разделяемое состояние, — между различ-

ными частями программы. Предположим, скажем, что у нас есть ссылочная ячейка и две функции,

работающие с ее состоянием:

c = ref 0;

c : Ref Nat

incc = λx : Unit . (c := succ (! c ); ! c);

incc : Unit -> Nat

decc = λx : Unit . (c := pred (! c ); ! c);

decc : Unit -> Nat

Вызов incc

incc unit ;

1 : Nat

приводит к изменению значения c, и это изменение можно наблюдать при вызове decc:

rev. 104

126 13.1. Введение

decc unit ;

0 : Nat

Если мы упакуем incc и decc в виде записи

o = { i = incc , d = decc };

o : { i: Unit -> Nat , d : Unit - > Nat }

то всю эту структуру можно передавать из функции в функцию как единое целое, и с помощью ее ком-

понент осуществлять операции увеличения и уменьшения разделяемой ячейки памяти c. В сущности,

мы построили простую разновидность объекта. Подробно эта идея будет изучена в Главе 18.

13.1.5. Ссылки на составные типы

Ссылочная ячейка не обязана содержать всего лишь число: наши примитивы позволяют создавать

ссылки на данные произвольного типа, включая функции. Можно, например, при помощи ссылок

реализовать (не очень, правда, эффективно) массивы чисел. Будем именем NatArray обозначать тип

Ref (Nat Nat).

Nat Array = Ref (Nat - > Nat );

Чтобы создать новый массив, мы выделяем ссылочную ячейку и записываем в нее функцию, которая

в ответ на любой индекс возвращает 0.

new array = λ_: Unit . ref (λn: Nat .0);

new array : Unit -> NatAr r ay

Чтобы получить элемент массива, просто применяем функцию к нужному индексу.

lo okup = λa: NatAr ray . λn : Nat . (! a) n;

lo okup : N atArray -> Nat -> Nat

Интересноая часть задачи кодирования — функция update. Она принимает массив, индекс и новое

значение, которое нужно сохранить в ячейке с этим индексом. Задачу свою она выполняет, создавая

(и сохраняя в ссылочной ячейке) новую функцию, которая, будучи спрошена о значении по данному

индексу, вернет новое значение, даноое в качестве аргумента update, а для всех остальных значений

индекса передаст задачу поиска функции, которая до сих пор хранилась в ссылочной ячейке.

up date = λa: NatAr ray . λm : Nat . λv : Nat .

let oldf = ! a in

a := (λn: Nat . if equal m n then v else oldf n ;)

up date : N atArray -> Nat -> Nat -> Unit

Упражнение 13.1.2 : Если бы мы определили update более компактно:

up date = λa: NatAr ray . λm : Nat . λv : Nat .

a := (λn: Nat . if equal m n then v else (! a) n ;)

было бы ее поведение тем же самым?

Ссылки на значения, содержащие другие ссылки, могут также быть очень полезны, и с их помо-

щью можно определять структуры данных вроде изменяемых списков и деревьев. (Как правило, такие

структуры также используют рекурсивные типы, о которых мы поговорим в Главе 20.)

13.1.6. Сборка мусора

Последний вопрос, который следует упомянуть, прежде чем мы перейдем к формальному опре-

делению ссылок – освобождение памяти. Мы не вводим в язык никаких элементарных операций для

освобождения ссылочных ячеек, когда они более не нужны. Вместо этого, подобно многим современным

языкам (включая ML и Java), мы полагаемся на то, что среда исполнения программ проводит сборку

мусора, собирая и освобождая ячейки, которые перестали быть доступными для программы. Это не

просто вопрос вкуса в проектировании языков: если в языке имеется явная операция освобождения

rev. 104

13.2. Типизация 127

памяти, достичь типовой безопасности становится крайне сложно. Причиной этому служит широко-

известная проблема висячих ссылок: мы выделям ячейку, содержащую число, сохраняем ссылку на

нее в некоторой структуре данных, какое-то время ей пользуемся, затем освобождаем ее и выделяем

новую ячейку, содержащую булевское значение, и при этом, возможно, используем то же самое место

в памяти. Теперь у нас может оказаться два имени для одной и той же ячейки памяти — одна с типом

Ref Nat, а другая с типом Ref Bool.

Упражнение 13.1.3 Покажите, как это может привсти к нарушению типовой безопасности.

13.2. Типизация

Правила типизации для ref, := и ! прямо следуют из поведения, которое мы им приписали.

Γ t

: T

Γ ref t

: Ref T

(T-Ref)

Γ t

: Ref T

Γ !t

: T

(T-Deref)

Γ t

: Ref T

Γ t

: T

Γ t

:=t

: Unit

(T-Assign)

13.3. Вычисление

Более тонкие вопросы семантики ссылок возникают, когда мы начинаем формализовывать их опе-

рационное поведение. Это легко увидеть, задав себе вопрос: «Как должны выглядеть значения типа

Ref T?» Основное наблюдение, которое нам придется учесть, состоит в том, что вычисление оператора

ref должно что-то делать — а именно, выделять память, — и результатом операции должна быть

ссылка на эту память.

Так что такое ссылка?

Память времени исполнения в большинстве реализаций языков программирования представляет

собой, в сущности, просто большой массив байтов. Среда времени исполнения следит, какие области в

этом массиве используются в каждый данный момент; когда нам требуется создать новую ссылочную

ячейку, мы выделяем достаточно большой сегмент из свободной области памяти (4 байта для целых

ячеек, 8 байт для ячеек, хранящих значения типа Float, и т. д.), отмечаем этот сегмент как использу-

емый, и возвращаем индекс его начала (как правило, в виде 32- или 64-битного целого). Эти индексы

и служат ссылками.

Для наших теперешних целей такая конкретика не нужна. Мы можем рассматривать память как

массив значений, а не байтов, абстрагируясь от того, что при исполнении различные значения имеют

представления разного размера. Кроме того, можно абстрагироваться от того, что ссылки (т. е., индексы

массива) являются числами. Таким образом, мы считаем, что ссылки являются элементами некоторого

неинтерпретируемого множества L адресов памяти, а все состояние памяти рассматриваем просто как

частичную функцию из адресов l в значения. Для состояний памяти мы используем метапеременную

µ. Таким образом, ссылка является адресом — абстрактным указателем в память. С этого момента мы

используем термин адрес, а не ссылка или указатель, считая его более абстрактным.

Теперь нам нужно расширить нашу операционную семантику и включить в нее состояния памяти.

Поскольку результат вычисления выражения в общем случае будет зависеть от содержимого памяти

Такой абстрактный подход к адресам не позволяет нам смоделировать арифметику указателей в низкоуровневых

языках вроде C. Это намеренное ограничение. Несмотря на то, что арифметика указателей изредка бывает очень полезна

(особенно при реализации низкоуровневых компонентов среды времени исполнения, скажем, сборщиков мусора), боль-

шинство систем типов не могут с ней формально работать: даже если мы знаем, что адрес n в памяти содержит Float,

это ничего нам не говорит о типе значения по адресу n 4. В C арифметика указателей — широко известный источник

нарушений типовой безопасности.

rev. 104

128 13.3. Вычисление

в момент вычисления, правила вычисления должны в качестве аргумента принимать не только терм,

но и состояние памяти. Более того, поскольку вычисление терма может вызвать побочные эффекты в

памяти, и эти эффекты могут повлиять на вычисление других термов в будущем, правила вычисления

должны возвращать новое состояние памяти. Таким образом, общий вид одношагового вычисления из

t t превращается в t µ t µ , где µ и µ — начальное и конечное состояние памяти. В сущности, мы

усложнили свое понятие абстрактной машины, так что состояние машины теперь состоит не только

из указателя команд (моделируемого термом), но еще и из текущего содержимого памяти.

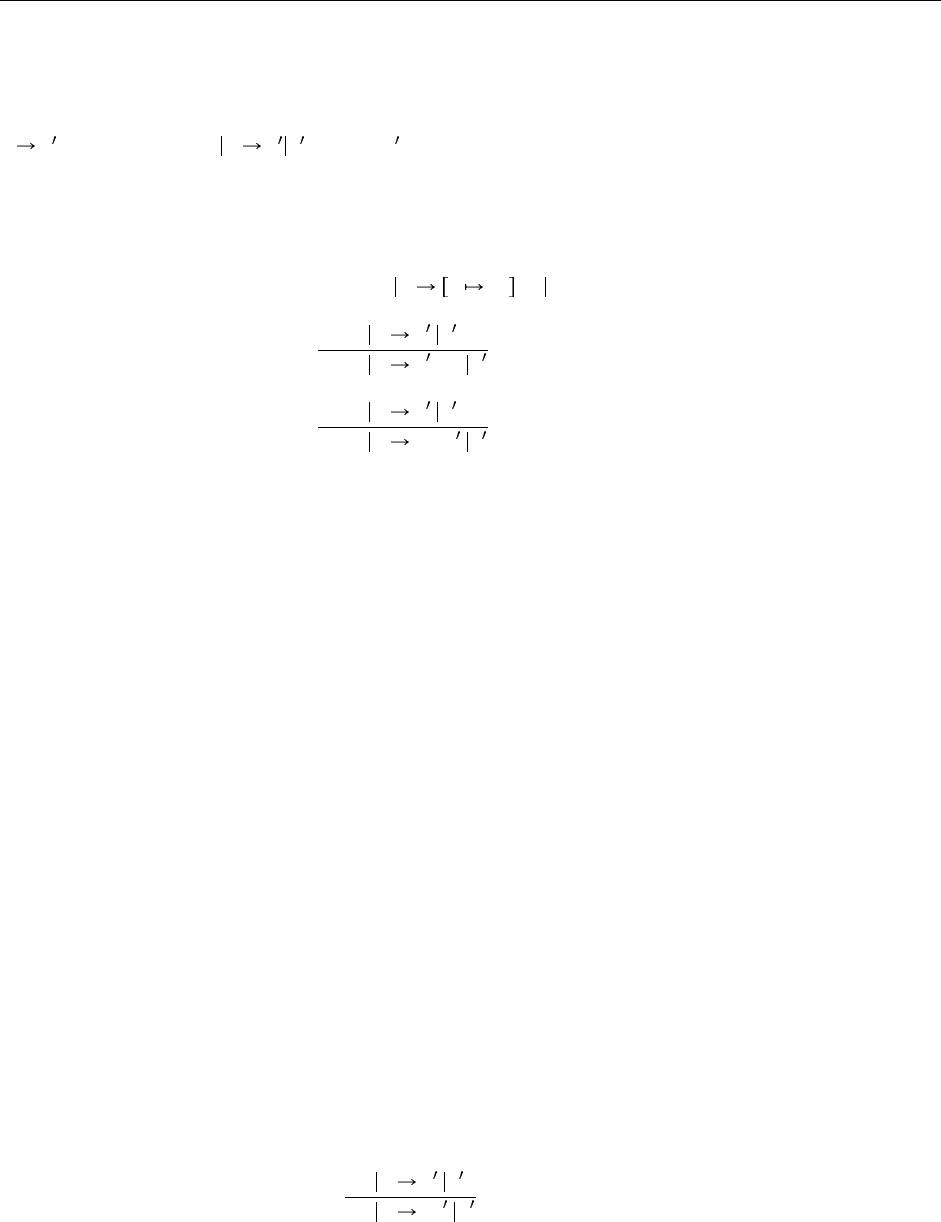
Чтобы осуществить это изменение, прежде всего мы должны дополнить все имеющиеся правила

вычисления состояниями памяти:

(λx:T

) v

µ x v

(E-AppAbs)

µ t

(E-App1)

µ t

µ v

(E-App2)

Обратите внимание, что первое из этих правил возвращает состояние памяти µ неизменным: при-

менение функции само по себе никаких побочных эффектов не имеет. Два других правила просто

распространяют побочные эффекты от предпосылки к заключению.

Затем нам требуется сделать небольшое дополнение в синтаксисе термов. Результатом вычисления

выражения ref будет новый адрес, и поэтому нам нужно включить адреса в множество возможных

результатов вычисления — т. е., в множество значений.

v ::= значения:

λx:T.t значение-абстракция

unit значение единичного типа

l адрес в памяти

Поскольку все значения являются термами, множество термов тоже должно включать адреса.

t ::= термы

x переменная

λx:T.t абстракция

t t применение

unit константа unit

ref t порождение ссылки

!t разыменование

t:=t присваивание

l адрес в памяти

Разумеется, такое расширение синтаксиса термов не означает, что мы хотим, чтобы программисты пи-

сали термы, явно упоминающие конкретные адреса: такие термы возникают только в качестве проме-

жуточных результатов вычисления. В сущности, слово «язык» в этой главе нужно рассматривать как

формализацию промежуточного языка, некоторые черты которого напрямую программистам недо-

ступны.

Пользуясь расширенным синтаксисом, мы можем сформулировать правила вычисления для новых

конструкций, работающих с адресами и содержимым памяти. Во-первых, чтобы вычислить выражение

разыменования !t

, нам сначала нужно редуцировать терм t

, пока он не превратится в значение:

µ t

µ !t

(E-Deref)

Когда t

сведен к значению, у нас должно получиться выражение вида !l, где l — некоторый адрес.

Терм, пытающийся разыменовать любое другое выражение, скажем, функцию или unit, ошибочен.

Правила вычисления в этом случае просто объявляют терм тупиковым. Теоремы о типовой безопасно-

сти из §13.5 позволяют нам считать, что правильно типизированные термы никогда в такой ситуации

rev. 104

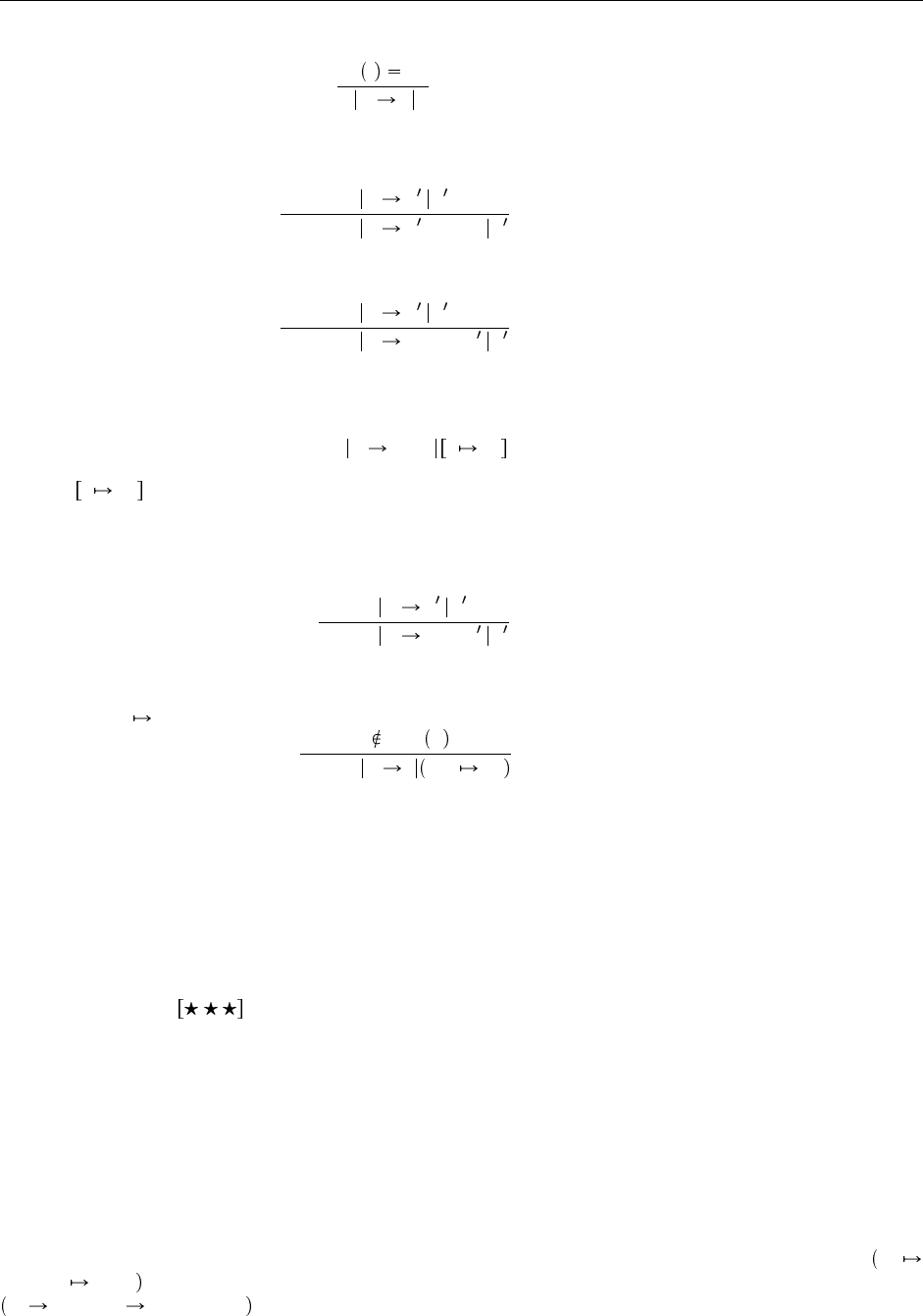
13.4. Типизация памяти 129

не окажутся.

µ l v

!l µ v µ

(E-DerefLoc)

Чтобы вычислить выражение присваивания t

:= t

, сначала мы вычисляем codet

, пока он не станет

значением (т. е., адресом),

µ t

:= t

µ t

:= t

(E-Assign1)

а затем вычисляем t

, пока оно тоже не станет значением (любого вида):

µ t

:= t

µ v

:= t

(E-Assign2)

Когда мы закончим вычислять t

и t

, у нас получится выражение вида l := v

, и мы выполняем

его путем обновления памяти — делаем так, чтобы по адресу l содержалось значение v

l := v

µ unit l v

(E-Assign)

(Запись l v

µ здесь означает «состояние памяти, отображающее l в v

, а остальные адреса туда же,

что и µ». Обратите внимание, что при этом шаге вычисления результирующим термом служит просто

unit; интересная часть результата — обновленное состояние памяти.)

Наконец, чтобы вычислить выражение вида ref t

, мы сначала вычисляем терм t

, пока он не

превратится в значение:

µ t

ref t

µ ref t

(E-Ref)

Затем, чтобы вычислить сам шаг ref, мы выбираем новый адрес l (т. е., адрес, который не входит в

имеющуюся область опеределения µ), и порождаем новое состояние памяти, расширяющее µ новым

связыванием l v

l dom µ

ref v

µ l µ, l v

(E-RefV)

Терм, получающийся в результате такого шага, — имя l свежевыделенного адреса в памяти.

Заметим, что наши правила вычисления не производят никакой сборки мусора: мы просто поз-

воляем памяти бесконечно расти по мере вычисления. Это не влияет на правильность результатов

вычисления (в конце концов, само определение «мусора» говорит, что это та часть содержимого памя-

ти, которая более недостижима и не играет никакой роли в дальнейшем вычислении), но означает, что

наивная реализация нашего вычислителя иногда будет исчерпывать имеющуюся память, в то время

как более разумно устроенный вычислеитель смог бы продолжить работу, заново используя адреса, чье

содержимое превратилось в мусор.

Упражнение 13.3.1 : Как можно уточнить наши правила вычисления, если мы хотим смоде-

лировать сборку мусора? Какую теорему потребуется доказать, чтобы продемонстрировать, что

наше улучшение работает правильно?

13.4. Типизация памяти

После того, как мы расширили синтаксис и правила вычисления, учтя наличие ссылок, нашей следу-

ющйей задачей будет написать правила типизации для новых конструкций — и, разумеется, убедиться,

что они непротиворечивы. Естественно, первый вопрос будет: «Каков тип адреса?».

Когда мы вычисляем терм, содержащий конкретные адреса, тип результата зависит от содержимого

памяти в начале вычисления. Например, если мы вычисляем терм !l

при состоянии памяти l

unit, l

unit , результатом будет unit; если тот же самый терм вычисляется при состоянии памяти

unit, l

λx:Unit.x , результат будет λx:Unit.x. По отношению к первому из этих состояний

rev. 104

130 13.4. Типизация памяти

содержимое адреса l

имеет тип Unit, по отношению ко второму — тип Unit Unit. Это наблюдение

немедленно ведет к первой попытке построить правило типизации для адресов:

Γ µ l : T

Γ l : Ref T

А именно, чтобы найти тип адреса l, мы смотрим на текущее содержимое ячейки с этим адресом и

вычисляем тип T

этого содержимого. Типом адреса тогда будет Ref T

Начав таким образом, мы должны продвинуться еще немного дальше, чтобы добиться непротиво-

речивого описания. В сущности, сделав тип терма зависимым от состояния памяти, мы превратили

трехместное отношение типизации (между контекстами, термами и типами) в четырехместное (между

контестами, содержимым памяти, термами и типами). Поскольку, с интуитивной точки зрения, со-

стояние памяти является частью контекста, в котором мы вычисляем тип терма, давайте при записи

помещать это состояние слева от символа : Γ µ t : T. Правило типизации для ссылок теперь имеет

вид

Γ µ µ l : T

Γ µ l : Ref T

и все прочие правила типизации в системе также расширяются состоянием памяти. Остальные пра-

вила не делают с этим состоянием ничего интересного — они просто передают его от предпосылки к

заключению.

Однако с этим правилом возникают две проблемы. Во-первых, проверка типов становится достаточ-

но неэффективной, поскольку вычисление типа адреса l включает вычисление типа текущего состояния

v по адресу l. Если l встречается в терме t много раз, мы будем пересчитывать тип v много раз в про-

цессе вывода дерева типизации для t. Хуже того, если сам v содержит адреса, нам придется и их тип

пересчитывать каждый раз, когда мы их встретим. Например, если состояние памяти таково:

λx:Nat. 999,

λx:Nat. (!l

) x,

λx:Nat. (!l

) x,

λx:Nat. (!l

) x,

λx:Nat. (!l

) x ,

то вычисление типа l

требует вычисления типов l

, l

и l

Во-вторых, предложенное правило типизации может вообще оказаться неспособным что-либо вы-

вести, если в памяти имеется цикл. Например, нет ни одного конечного дерева вывода типизации для

адреса l

по отношению к памяти

λx:Nat. (!l

) x

λx:Nat. (!l

) x),

поскольку вычисление типа для l

требует нахождения типа для l

, который, в свою очередь, обраща-

ется к l

, и т. д. Такие циклические структуры ссылок действительно иногда встречаются на практике

(скажем, с их помощью можно построить двусвязные списки), а нам хотелось бы, чтобы наша система

типов умела работать с такими данными.

Упражнение 13.4.1 : Можете ли Вы найти терм, который при вычислении создал бы такое цик-

лическое состояние памяти?

Обе эти проблемы возникают из-за того, что наше предварительное правило типизации для адресов

требует пересчитывать тип адреса каждый раз, когда он упоминается в терме. Однако интуитивно ясно,

что это необязательно. В конце концов, когда адрес впервые создается, мы знаем, каков тип начального

значения, которое мы по этому адресу записываем. Более того, несмотря на то, что впоследствии мы

можем сохранять в той же ячейке другие значения, эти другие значения всегда будут того же типа, что

и начальное. Другими словами, для каждого адреса в памяти мы всегда имеем в виду один конкретный

тип, определяемый в момент выделения памяти. Эти типы можно собрать вместе в структуру типи-

зации памяти — конечную функцию, отображающую адреса в типы. Для обозначения таких функций

мы будем использовать метапеременную Σ.

rev. 104