Пирс Б. Типы в языках программирования
Подождите немного. Документ загружается.


11.5. Связывания LET 101
($\ L$f : UU . f unit ) ( $ \ L$x : Unit . x );
Во время проверки типов эти сокращения по необходимости разворачиваются. С другой стороны, про-
цедуры проверки типов пытаются по возможности эти определения свернуть. (А именно, каждый раз,
проверяя подтерм, они смотрят, не подпадает ли его тип в точности под какое-нибудь из известных
сокращений.) Обычно при этом получаются разумные результаты, но изредка нам требуется распеча-
тывать тип иначе, либо из-за того, что простая стратегия соспоставления с образцом не дает программе
проверки типов схлопнуть сокращение (скажем, в системах, где разрешается изменять порядок имено-
ванных полей типов записи, она не поймет, что {a:Bool, b:Nat} можно свободно заменять на {b:Nat,
a:Bool}), либо из-за того, что нам по какой-то причине хочется распечатывать тип иначе. К примеру,
в
λf : Unit -> Unit . f ;
<fun > : ( Unit -> Unit ) -> UU
сокращение UU применено к результату функции, но не применено к ее аргументу. Если нам хочется,
чтобы тип распечатывался как UU, нужно либо изменить аннотацию типа на выражении-абстракции
λf :UU . f;
<fun > : UU -> UU
либо явно приписать тип всей абстракции:
(λf : Unit -> Unit . f) as UU -> UU ;
<fun > : UU -> UU
Когда процедура проверки типов обрабатывает приписывание типа t as T, она разворачивает каждое
сокращение в T, проверяя, что t имеет тип T, однако затем возвращает сам T, в точности как он был за-
писан, в качестве типа выражения-приписывания. Использование приписываний типа для управления
печатью типов — особенность именно интерпретаторов, сопровождающих эту книгу. В полноразмерном
языке программирования механизмы для сокращения и распечатки типов либо не нужны (например,
в Java все типы представляются короткими именами — см. Главу 19), либо намного теснее привязаны
к языку (как в OCaml — см. R´emy and Vouillon 1998; Vouillon 2000).
Наконец, приписывание типов будет обсуждаться в §15.5, и будет служить механизмом абстракции.
В системах, где один и тот же терм t может иметь несколько типов (скажем, в системах с наследовани-
ем), через приписывание можно «спрятать» некоторые из этих типов, указав программе проверки, что
t нужно рассматривать, как будто бы он обладал меньшим набором типов. Кроме того, в §15.5 будет
обсуждаться связь между явным приписыванием типов и их преобразованием.
Упражнение 11.4.1 Рекомендуется, : (1) Покажите, как приписывание типов можно предста-
вить в виде производной формы. Докажите, что «официальные» правила типизации и вычисления
должным образом соотвествуют Вашему определению. (2) Предположим, что вместо пары правил
вычисления E-Ascribe и E-Ascribe1, мы ввели «энергичное» правило
t
1
as T t
1
(E-AscribeEager)
немедленно выкидывающее конструкцию с приписыванием при обнаружении. Можно ли при этом
по-прежнему считать приписывание типа производной формой?
11.5. Связывания let
При написании сложного выражения часто бывает полезно — как для того, чтобы избежать по-
вторений, так и для улучшения читаемости, — присвоить имена некоторым его подвыражениям. В
большинстве языков имеются способы сделать это. Например, в ML запись let x = t
1
in t
2
означает
«вычислить выражение t
1
и связать имя x с получившимся значением при вычислении t
2
».
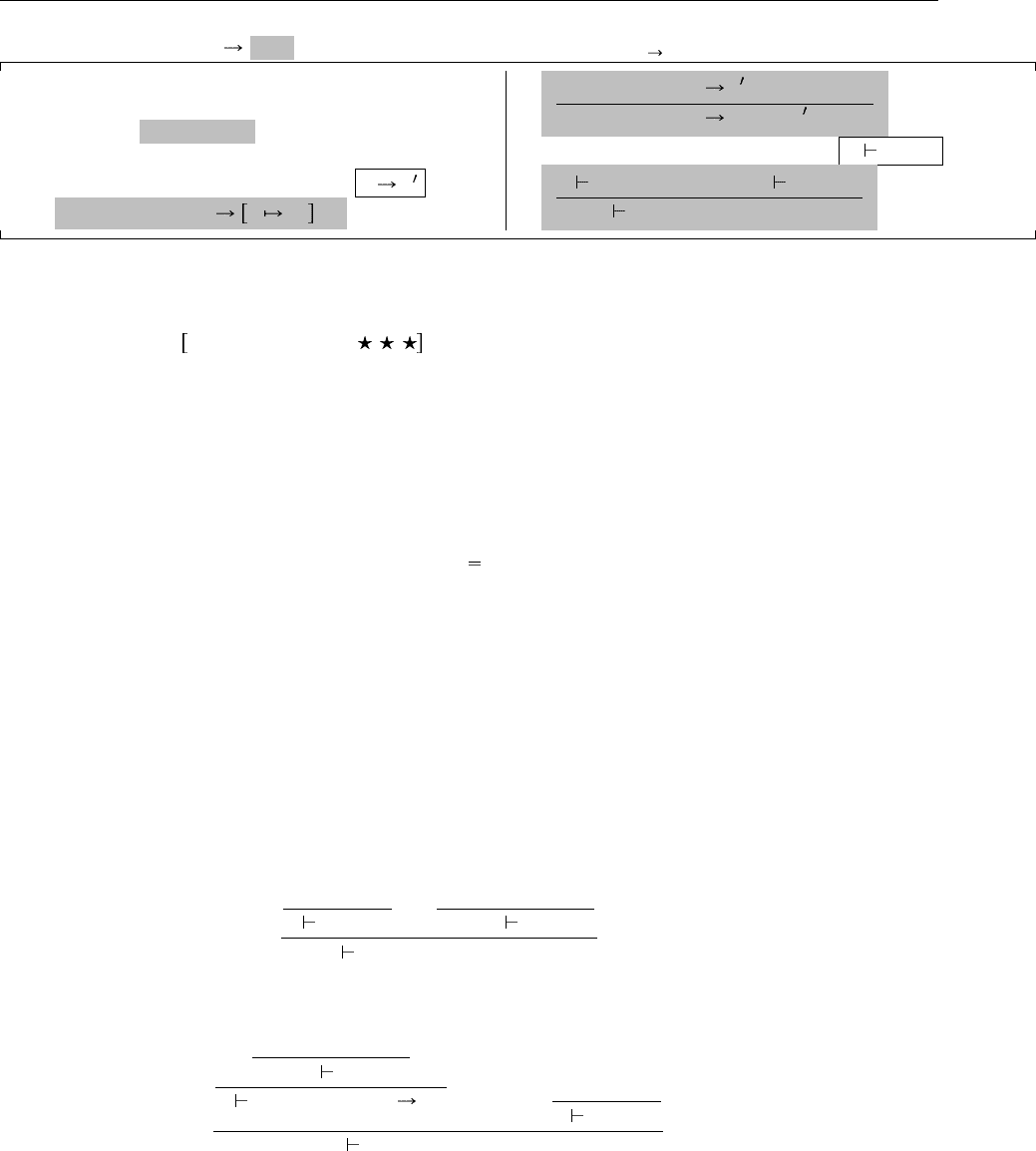
Наша конструкция связывания через let (представленная на Рис. 11.4), подобно ML, следует по-
рядку вычисления с вызовом по значению, то есть, терм, связанный через let, должен быть полностью
вычислен, прежде чем начнет вычисляться тело let-формы. Правило типизации T-Let указывает,
что тип let-выражения можно получить, определив сначала тип связанного терма, расширив контекст
связыванием с этим типом, и вычислив в этом расширенном контексте тип тела let, который и будет
тогда типом всего let-выражения.
rev. 104
102 11.5. Связывания LET
let Расширяет λ (9.1)
Новые синтаксические формы
t ::= . . . термы:
let t in t связывание let
Новые правила вычисления t t
let x=v
1
in t
2
x v
1
t
2
(E-LetV)
t
1
t
1
let x=t
1
in t
2
let x=t
1
in t
2
(E-Let)
Новые правила типизации Γ t : T
Γ t
1
: T
1
Γ, x:T
1
t
2
: T
2
Γ let x=t
1
in t
2
: T
2
T-Let
Рис. 11.4. Связывание let
Упражнение 11.5.1 Рекомендуется, : Программа проверки типов letexercise (ее можно
скачать на сайте книги) является неполной реализацией let-выражений: наличествуют простые
функции синтаксического анализа и распечатки, но в функциях eval1 и typeof нет вариантов для
конструктуора TmLet (на их месте вы найдете заглушки, которые сопоставляются с чем угодно, а
при попытке исполнения завершают программу с сообщением об ошибке). Допишите программу.
Можно ли определить let в виде производной формы? Да, как показал Ландин; однако детали реа-
лизации несколько сложнее, чем для последовательного исполнения и приписывания типов. С наивной
точки зрения, ясно, что эффекта let-связывания можно достичь, сочетая абстракцию и применение:
let x=t
1
in t
2
def
(λx:T
1
.t
2
) t
1
Заметим, однако, что правая часть определения включает аннотацию типа T
1
, которая на левой сто-
роне отсутствует. А именно, если мы считаем, что производные формы подвергаются удалению сахара
в процессе синтаксического анализа компилятором, то нам нужно понять, откуда синаксический анали-
затор узнает, что в качестве аннотации типа в λ-выражении для обессахаренного терма на внутреннем
языке он должен породить T
1
.
Ответ на этот вопрос, разумеется, таков: информация приходит из программы проверки типов!
Требуемая аннотация типов получается путем вычисления типа терма t
1
. С более формальной точки
зрения, у нас выходит, что конструктор let — производная форма несколько иного рода, чем виденные
нами до сих пор: ее нужно рассматривать не как обессахаривающее преобразование термов, а как
преобразование на деревьях вывода типов (или, если Вам так удобнее считать, на термах, которые
процедура проверки типов пометила результатами своего анализа). При этом дерево, включающее let
.
.
.
Γ t
1
: T
1
.
.
.
Γ, x:T
1
t
2
: T
2
Γ let x=t
1
in t
2
: T
2
T-Let
переводится в дерево, включающее абстракцию и применение:
.
.
.
Γ, x:T
1
t
2
: T
2
Γ λx:T
1
.t
2
: T
1
T
2
T-Abs
.
.
.
Γ t
1
: T
1
Γ (λx:T
1
.t
2
) t
1
: T
2
T-App
Таким образом, let — «несколько менее производная» форма, чем уже виденные нами: ее поведение
при вычислении можно определеить через удаление сахара, но ее поведение с точки зрения типизации
должно быть встроено во внутренний язык.
В Главе 22 мы встретим еще один довод против определения let в виде производной формы: в язы-
ках с полиморфизмом по Хиндли-Милнеру (т. е., на основе унификации), программа проверки типов
обрабатывает let-формы особым образом и с их помощью обобщает полиморфные определения, полу-
чая при этом типы, которые нельзя смоделировать через обыкновенную λ-абстракцию и применение.
rev. 104
11.6. Пары 103
Расширяет λ (9.1)
Новые синтаксические формы
t ::= . . . термы:
{t,t} пара
t.1 первая проекция
t.2 вторая проекция
v ::= . . . значения:
{v,v} значение-пара
T ::= . . . типы:
T
1
T
2
тип-произведение
Новые правила вычисления t t
{v
1
,v
2
}.1 v
1
(E-PairBeta1)
{v
1
,v
2
}.2 v
2
(E-PairBeta2)
t
1
t
1
t
1
.1 t
1
.1
(E-Proj1)
t
1
t
1
t
1
.2 t
1
.2
(E-Proj2)
t
1
t
1
{t
1
,t
2
} {t
1
,t
2
}
(E-Pair1)
t
2
t
2
{v
1
,t
2
} {v
1
,t
2
}
(E-Pair2)
Новые правила типизации Γ t : T
Γ t
1
: T
1
Γ t
2
: T
2
Γ {t
1
,t
2
} : T
1
T
2
(T-Pair)
Γ t
1
: T
11
T
12
Γ t
1
.1 : T
11
(T-Proj1)
Γ t
1
: T
11
T
12
Γ t
1
.2 : T
12
(T-Proj2)
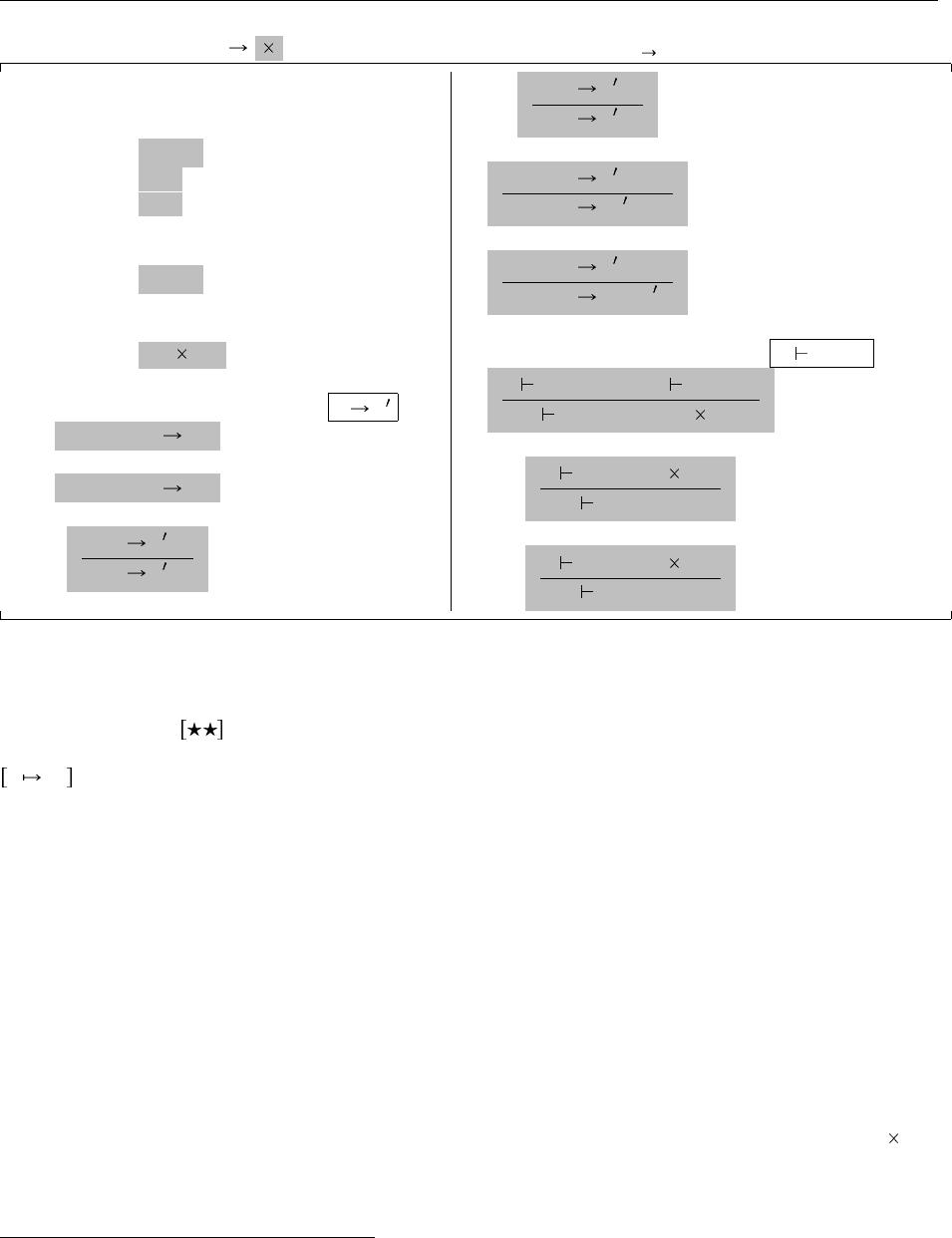
Рис. 11.5. Пары
Упражнение 11.5.2 : Можно попытаться определить удаление сахара в форме let через ее немед-
ленное «вычисление» — т. е., рассматривать let x=t
1
in t
2
как сокращение для подстановки в тело
x t
1
t
2
. Насколько хороша эта идея?
11.6. Пары
В большинстве языков программирования имеются различные способы построения составных струк-
тур данных. Простейший из таких способов – пары, или, в более общем случае, кортежи. В этом
разделе мы рассматриваем пары, а более общие конструкции — кортежи и записи с метками полей, —
откладываем до §11.7 и §11.8.
3
Формальное определение пар едва ли стоит подробного обсуждения — для читателя, добравшегося
до этого места в книге, чтение правил на Рис. 11.5 должно быть едва ли не проще, чем текст на
естественном языке, содержащий ту же самую информацию. Давайте, однако, рассмотрим вкратце
различные детали определения, чтобы подчеркнуть общую структуру.
Чтобы добавить пары к простому типизированному лямбда-исчислению, требуется два новых вида
термов: порождение пары, записываемое {t
1
,t
2
}, и проекция, записываемая t.1 в случае, если это
первая проекция, и t.2, если это вторая проекция, — а также новый конструктор типов T
1
T
2
,
называемый произведение (или, иногда, декартово произведение) типов T
1
и T
2
. Пары записываются в
фигурных скобках,
4
чтобы подчеркнуть их связь с записями из §11.8.
В правилах вычисления нужно указать, как ведут себя пары и их проекции. Правила E-PairBeta1
3
В интерпретаторе fullsimple синтаксис пар, приводимый здесь, не поддерживается, поскольку кортежи все равно
являются более общим решением.
4
Способ записи с фигурными скобками не вполне удачен для пар и кортежей, поскольку напоминает стандартное
математическое обозначение множеств. Чаще используются круглые скобки, как в популярных языках вроде ML, так и в
исследовательской литературе. Встречаются также и другие виды нотации, например, квадратные или угловые скобки.
rev. 104
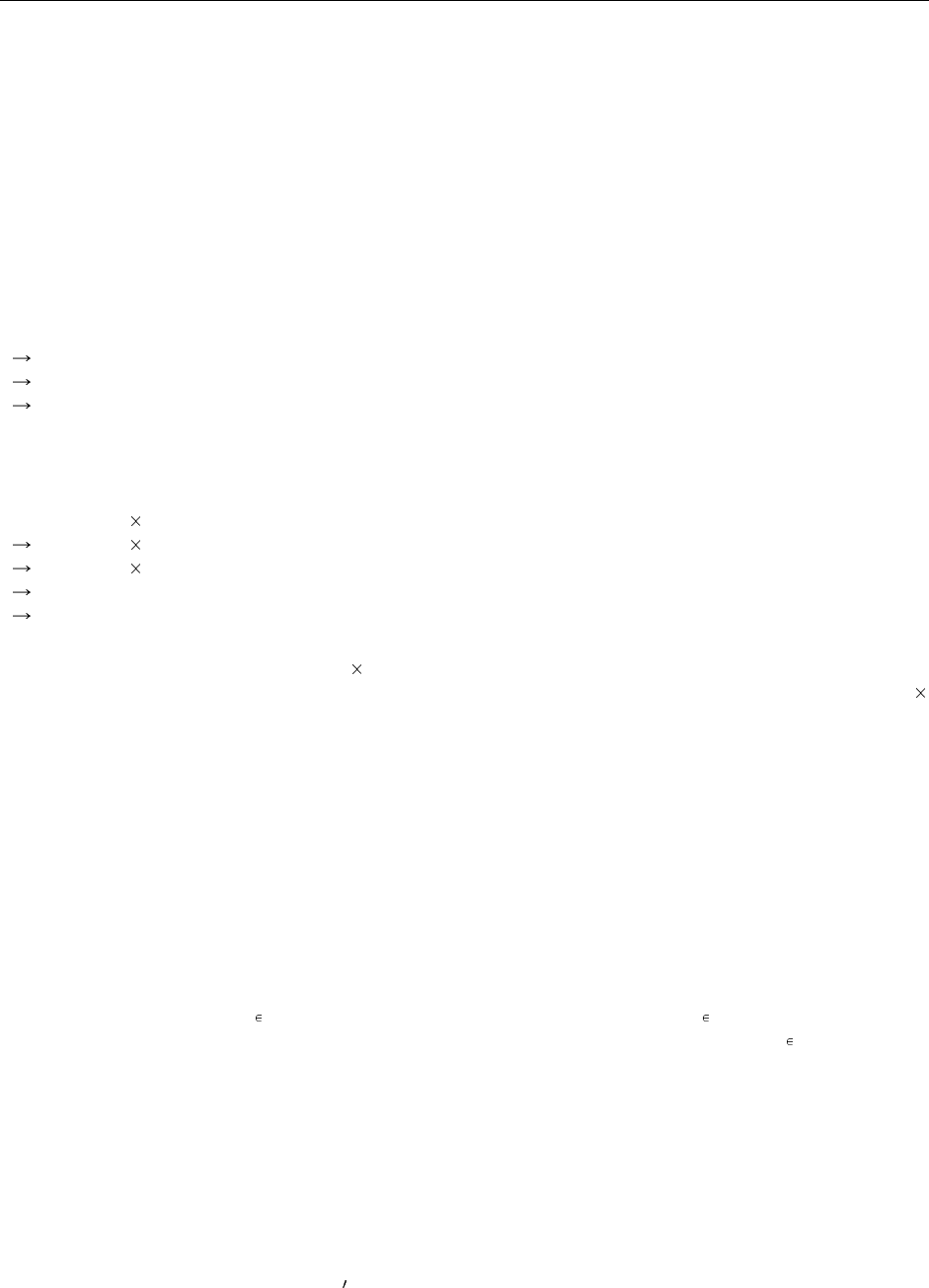
104 11.7. Кортежи
и E-PairBeta2 указывают, что при сочетании полностью вычисленной пары с первой или второй
проекцией результатом является соответствующая компонента пары. E-Proj1 и E-Proj2 позволяет
производить вычисления внутри проекций, если терм, из которого производится проекция, еще не
полностью вычислен. E-Pair1 и E-Pair2 вычисляют части пары: сначала левую, а затем — когда
слева окажется значение, — правую часть.
Порядок, возникающий из использования метапеременных v и t в этих правилах, обеспечивает для
пар стратегию вычисления слева направо. Например, составной терм
{pred 4, if true then false else false}.1
вычисляется (только) так:
{pred 4, if true then false else false}.1
{3, if true then false else false}.1
{3, false}.1
3
Кроме того, нам нужно добавить новый вариант к определению значений, и указать, что {v
1
, v
2
}
является значением. То, что компоненты пары-значения сами обязаны быть значениями, обеспечивает
полное вычисление пары, передаваемой как аргумент функции, прежде чем начнет выполняться тело
функции. Например:
(λx:Nat Nat. x.2) {pred 4, pred 5}
(λx:Nat Nat. x.2) {3, pred 5}
(λx:Nat Nat. x.2) {3,4}
{3,4}.2
4
Правила типизации для пар и их проекций не представляют сложности. Правило введения T-Pair
указывает, что {t
1
, t
2
} имеет тип T
1
T
2
, при условии, что t
1
имеет тип T
1
, а t
2
— тип T
2
. Соответ-
ственно, правила удаления T-Proj1 и T-Proj2 говорят, что, если t
1
имеет тип-произведение T
11
T
12
(т. е., если этот терм даст в качестве значения пару), то типами проекций этой пары будут T
1
и T
2
.
11.7. Кортежи
Понятие двухаргументного произведения типов из предыдущего раздела нетрудно расширить до
n-местных произведений, называемых кортежами. Например, {1,2,true} — 3-х местный кортеж, со-
держащий два числа и булевское значение. Его тип записывается как {Nat,Nat,Bool}.
Единственная трудность при таком обобщении состоит в том, что требуется придумать способ за-
писи, единообразно описывающий структуры произвольного размера; такие соглашения всегда пред-
ставляют некоторую сложность из-за неизбежного компромисса между точностью и читаемостью. Мы
используем обозначение {t
i
i 1..n
} для кортежа из n членов, от t
1
до t
n
, и {T
i
i 1..n
} для его типа. Заме-
тим, что при этом n может равняться нулю; в таком случае, диапазон 1..n пуст, а {t
i
i 1..n
} равняется
{}, пустому кортежу. Кроме того, обратите внимание на различие между простым значением вроде 5 и
одноэлементным кортежом вроде {5}: единственная операция, которую можно произвести с последним
— извлечение первой компоненты.
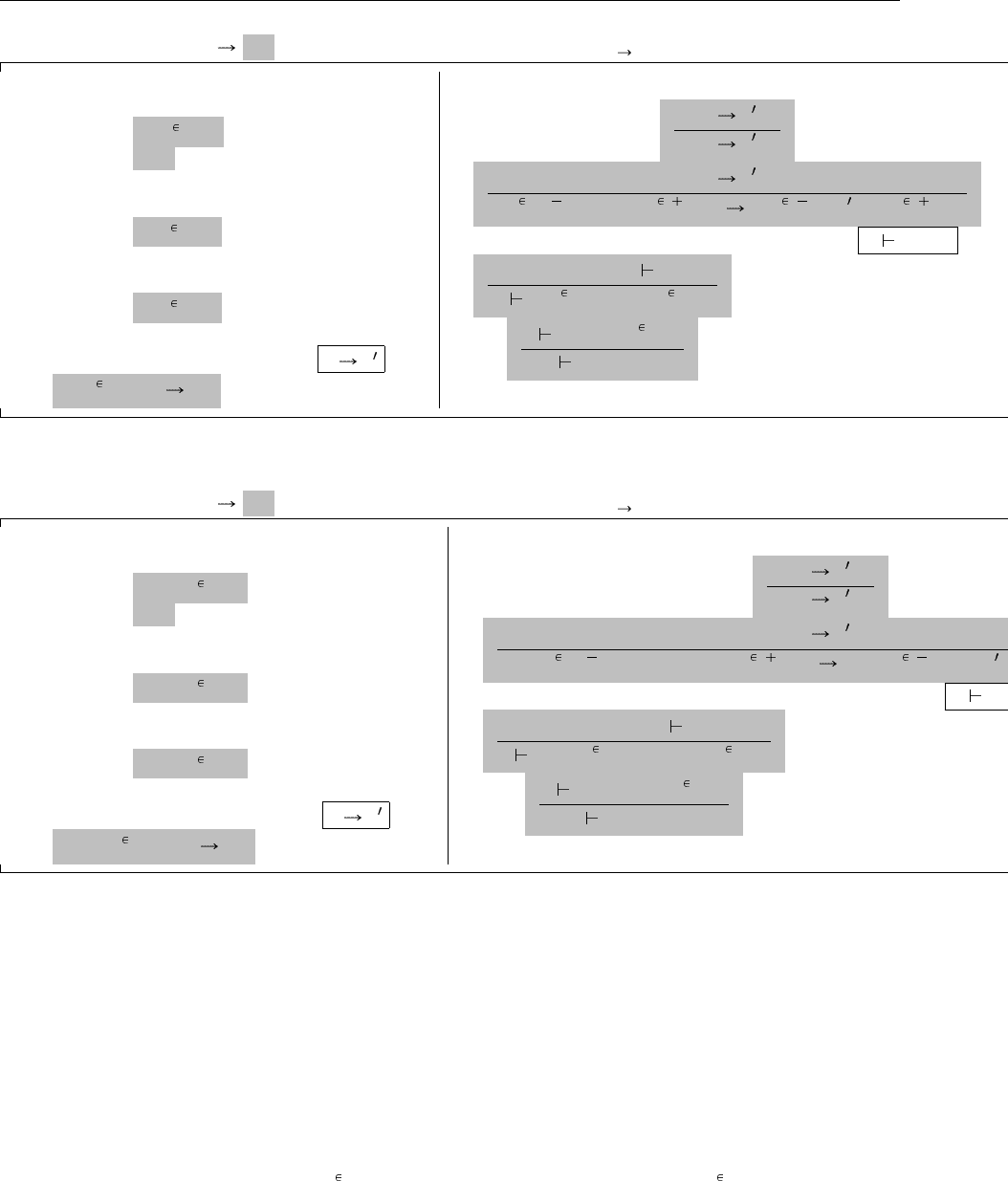
Рис. 11.6 дает формальное определение кортежей. Оно похоже на определение типов-произведений
(Рис. 11.5), только каждое правило для пар обобщено до случая с n членами, и каждая пара правил для
первой и второй проекции превращается в единственное правило для произвольной проекции кортежа.
Единственное правило, заслуживающее отдельного внимания – E-Tuple, сочетающее и обобщающее
правила E-Pair1 и E-Pair2 на Рис. 11.5. На естественном языке его смысл выражается так: если
имеется кортеж, где все поля слева от поля j уже преобразованы в значения, то можно проделать один
шаг вычисления этого поля, из t
j
в t
j
. Как и раньше, при помощи метапеременных мы обеспечиваем
стратегию вычисления слева направо.
rev. 104
11.8. Записи 105
{} Расширяет λ (9.1)
Новые синтаксические формы
t ::= . . . термы:
{t
1
i 1..n
} кортеж
t.i проекция
v ::= . . . значения:
{v
i
i 1..n
} кортеж-значение
T ::= . . . типы:
{T
i
i 1..n
} тип записей
Новые правила вычисления t t
{v
i
i 1..n
}.j v
j
(E-ProjTuple)
t
1
t
1
t
1
.i t
1
.i
(E-Proj)
t
j
t
j
{v
i
i 1..j 1
, t
j
, t
k
k j 1..n
} {v
i
i j 1
, t
j
, t
k
k j 1..n
}
(E-Tuple)
Новые правила типизации Γ t : T
для каждого i, Γ t
i
: T
Γ {t
i
i 1..n
} : {T
i
i 1..n
}
(T-Tuple)
Γ t
1
: {T
i
i 1..n
}
Γ t
1
.j : T
j
(T-Proj)
Рис. 11.6. Кортежи
{} Расширяет λ (9.1)
Новые синтаксические формы
t ::= . . . термы:
{l
i
=t
i
i 1..n
} запись
t.l проекция
v ::= . . . значения:
{l
i
=v
i
i 1..n
} запись-значение
T ::= . . . типы:
{l
i
:T
i
i 1..n
} тип записей
Новые правила вычисления t t
{l
i
=v
i
i 1..n
}.l
j
v
j
(E-ProjRcd)
t
1
t
1
t
1
.l t
1
.l
(E-Proj)
t
j
t
j
{l
i
=v
i
i 1..j 1
, l
j
=t
j
, l
k
=t
k
k j 1..n
} {l
i
=v
i
i j 1
, l
j
=t
j
, l
k
=t
k
k j 1..n
}
(E-Rcd)
Новые правила типизации Γ t : T
для каждого i, Γ t
i
: T
i
Γ {l
i
=t
i
i 1..n
} : {l
i
:T
i
i 1..n
}
(T-Rcd)
Γ t
1
: {l
i
:T
i
i 1..n
}
Γ t
1
.l
j
: T
j
(T-Proj)
Рис. 11.7. Записи
11.8. Записи
Переход от n-местных кортежей к записям с помеченными полями также не представляет тру-
да. Мы просто снабжаем каждое поле t
i
меткой, выбираемой из некоторого заранее заданного мно-
жеста L. Например, {x=5} и {partno=5524,cost=30.27} — записи-значения; их типы — {x:Nat} и
{partno:Nat,cost:Float}. Мы требуем, чтобы все метки полей в каждом данном терме-записи или
типе записи были различны.
Правила для записей сведены в таблицу на Рис. 11.7. Единственное из них, достойное отдельного
упоминания, — E-ProjRcd, где мы опираемся на не вполне формальное соглашение. Правило следует
понимать так: если есть запись {l
i
=v
i
i 1..n
} с меткой j-того поля codel
j
, то {l
i
=v
i
i 1..n
}.l
j
за один шаг
переходит в j-ое значение поля, v
j
. От этого соглашения (и от подобного ему соглашения для кортежей
в правиле E-ProjTuple) можно было бы избавиться и переформулировать правило в более явном
виде; однако при этом мы слишком сильно проиграли бы в читабельности.
rev. 104
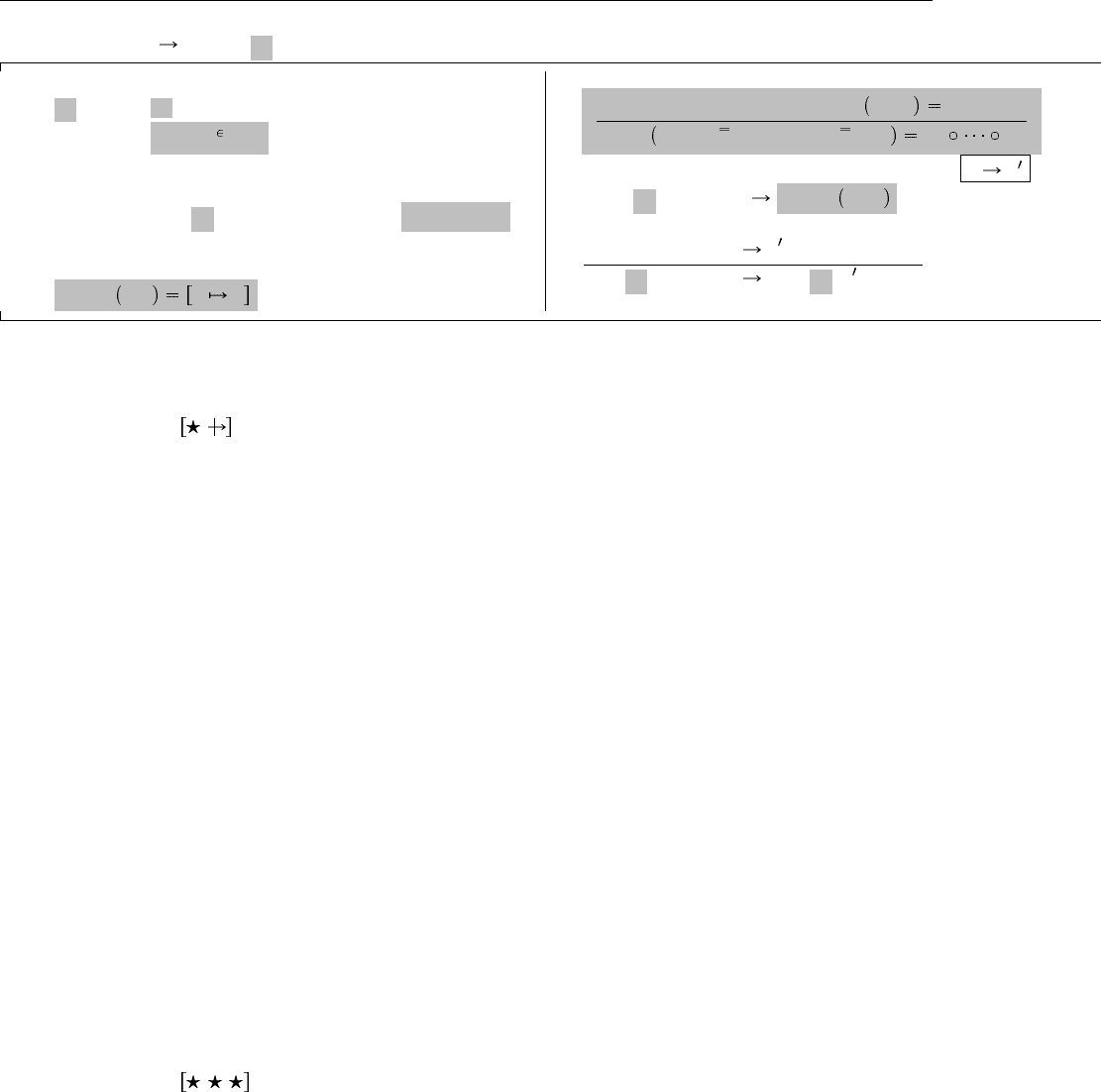
106 11.8. Записи
{} let p (бестиповое) Расширяет 11.7 и 11.4
Новые синтаксические формы
p ::= x образец-переменная
{l
i
=p
i
i 1..n
} образец для записи
t ::= . . . термы:
let p in t связывание с образцом
Правила сопоставления
match x, v x v (M-Var)
для каждогоi, match p
i
, v
i
σ
i
match {l
i
=p
i
i 1..n
},{l
i
=v
i
i 1..n
} σ
1
σ
n
(M-Rcd)
Новые правила вычисления t t
let p =v
1
in t
2
match p, v
1
t
2
(E-LetV)
t
1
t
1
let p =t
1
in t
2
let p =t
1
in t
2
(E-Let)
Рис. 11.8. (Бестиповые) образцы для записей
Упражнение 11.8.1 : Запишите, для сравнения, E-ProjRcd в явном виде.
Обратите внимание, что в верхнем углу блока правил, определяющих кортежи и записи, стоит од-
на и та же «метка конструкции» {}. В самом деле, кортежи можно считать особым случаем записей,
просто разрешив в качестве меток полей натуральные числа, наряду со словами-идентификаторами.
В случае, когда i-ое поле записи имеет метку i, мы эту метку опускаем. Например, {Bool,Nat,Bool}
будет считаться сокращенной записью для {1:Bool,2:Nat,3:Bool}. (Такое соглашение разрешает да-
же смешивать именованные поля с нумерованными, и писать {a:Bool.Nat,c:Bool} как сокращение
{a:Bool,2:Nat,c:Bool}, однако такая вольность на практике вряд ли будет полезна.) Во многих язы-
ках кортежи и записи считаются разными типами из более практических соображений: они по-разному
реализуются компилятором.
Языки программирования различаются в том, как они относятся к порядку полей в записях.
Во многих языках порядок полей как в значениях-записях, так и в определениях их типов никак
не влияет на значение — т. е., термы {partno=5524,cost=30.27} и {cost=30.27,partno=5524} зна-
чат одно и то же и имеют один и тот же тип, записываемый либо {partno:Nat,cost:Float}, либо
{cost:Float,partno=Nat}. Мы приняли другое решение: в этом тексте {partno=5524,cost=30.27} и
{cost=30.27,partno=5524} представляют собой разные значения, с типами {partno:Nat,cost:Float}
и {cost:Float,partno=Nat}, соответственно. В Главе 15 мы примем новую, менее строгую, точку зре-
ния на порядок полей, и введем отношение наследования, в котром типы {partno:Nat,cost:Float} и
{cost:Float,partno=Nat} будут эквивалентны — каждый из них будет наследником другого, — так
что термы одного типа можно будет всегда использовать там, где ожидается значение другого из них.
(В присутствии наследования выбор между неупорядоченными и упорядоченными записями серьез-
но влияет на производительность; это обсуждается в дальнейшем, в §15.6. Однако когда мы решим,
как получить неупорядоченииые записи, выбор, иметь ли записи неупорядоченными с самого начала
или считать поля на низком уровне упорядоченными, а затем ввести правила, позволяющие этот по-
рядок игнорировать, становится делом вкуса. Мы выбрали второй вариант для того, чтобы получить
возможность обсудить оба.)
Упражнение 11.8.2 : В нашем описании записей операция проекции позволяет извлечь поля
записи по одному. Многие высокоуровневые языки программирования обладают альтернативной син-
таксической конструкцией сопоставления с образцом, где все поля записи можно извлечь одновремен-
но. Такая конструкция позволяет сильно сократить многие программы. Как правило, образцы могут
вкладываться друг в друга, и таким образом можно легко извлекать данные из сложных вложенных
структур данных.
Можно добавить простую разновидность сопоставления с образцом к бестиповому лямбда-
исчислению, введя новую синтаксическую категорию образцов, а также новый вариант (для самой
конструкции соспоставления) к синтаксису термов. (См. Рис. 11.8.)
Правило вычисления для сопоставления с образцом является обобщенным случаем для правила
let-связывания с Рис. 11.4. Оно опирается на вспомогательную «сопоставляющую» функцию, кото-
rev. 104

11.9. Типы-суммы 107
рая, принимая образец p и значение v, либо терпит неудачу (что означает, что значение v пе со-
ответствует образцу), либо выдает в качестве результата подстановку, переводящую переменные,
содержащиеся в p, в соответствующие части v. Например, match {x, y}, {5, true} порождает
подстановку x 5, y true , сопоставление match x, {5, true} порождает x {5, true} , а
match {x}, {5, true} терпит неудачу. Правило E-LetV с помощью match вычисляет подстановку
для переменных в p.
Сама функция match определяется отдельным набором правил вывода. Правило M-Var утвержда-
ет, что сопоставление с переменной всегда завершается успешно, и возвращает подстановку, пере-
водящую переменную в значение, с которым производится сопоставление. Правило M-Rcd говорит,
что, для того, чтобы сопоставить образец-запись {l
i
=p
i
i 1..n
} со значением-записью {l
i
=v
i
i 1..n
}
(при этом у них должна быть одинаковая длина и одинаковые метки полей), нам нужно по отдель-
ности сопоставить каждый подобразец p
i
с соответствующим подзначением v
i
, получая при этом
подстановку σ
i
, и построить окончательный результат в виде композиции всех таких подстано-
вок. (Мы требуем, чтобы ни одна переменная не встречалась в образце более одного раза, так что
композиция подстановок будет просто их объединением.)
Покажите, как к этой системе добавить типы.
1. Введите правила типизации для новых конструкций (при этом Вы можете делать любые нуж-
ные Вам изменения в синтаксисе).
2. Постройте план доказательства теорем о сохранении и продвижении для всего полученного ис-
числения. (Строить полные доказательства необязательно; достаточно сформулировать тре-
буемые леммы и расположить их в правильном порядке.)
11.9. Типы-суммы
Во многих программах требуется работать с гетерогенными наборами данных. К примеру, вершина
в бинарном дереве может быть либо концевой, либо внутренней вершиной с двумя дочерними; подобным
образом, список может быть либо пустым (nil), либо cons-ячейкой, состоящей из головы и хвоста,
5
вершина абстрактного синтаксического дерева внутри компилятора может представлять переменную,
абстракцию, применение функции и т. д. Механизм теории типов, поддерживающий программирование
такого рода, называется вариантные типы.
Прежде чем ввести варианты в общем случае (§11.10), рассмотрим сначала более простой случай
бинарных типов-сумм. Тип-сумма описывает множество значений, выбираемых ровно из двух данных
типов. Допустим, например, что у нас есть типы
ФизАдрес
= фио{: String , адрес: String };ВиртАдрес
= имя{: String , email : String };
представляющие различные виды записей в адресной книге. Если мы хотим обрабатывать оба вида за-
писей единообразно (например, если нам требуется построить список, содержащий записи обоих видов),
можно ввести тип-сумму
6
Адрес
= ФизАдрес + ВиртАдрес;
каждый из элементов которого представляет собой либо ФизАдрес, либо ВиртАдрес.
Элементы этого типа создаются путем постановки тегов на элементы типов-компонент ФизАдрес
и ВиртАдрес. Например, если pa имеет тип ФизАдрес, то inl pa будет иметь тип Адрес. (Имена тегов
inl и inr помогают представить их как функции
inl : ФизАдрес -> ФизАдресВиртАдрес+;
inr : ВиртАдрес -> ФизАдресВиртАдрес+;
5
Эти примеры, подобно большинству случаев реального использования вариантных типов, используют также рекур-
сивные типы — хвост списка сам является списком, и т. д. К рекурсивным типам мы вернемся в Главе 20.
6
Интерпретатор fullsimple на самом деле не поддерживает описанные здесь конструкции с бинарными суммами —
вместо этого есть более общая конструкция с вариантами, описанная ниже.
rev. 104
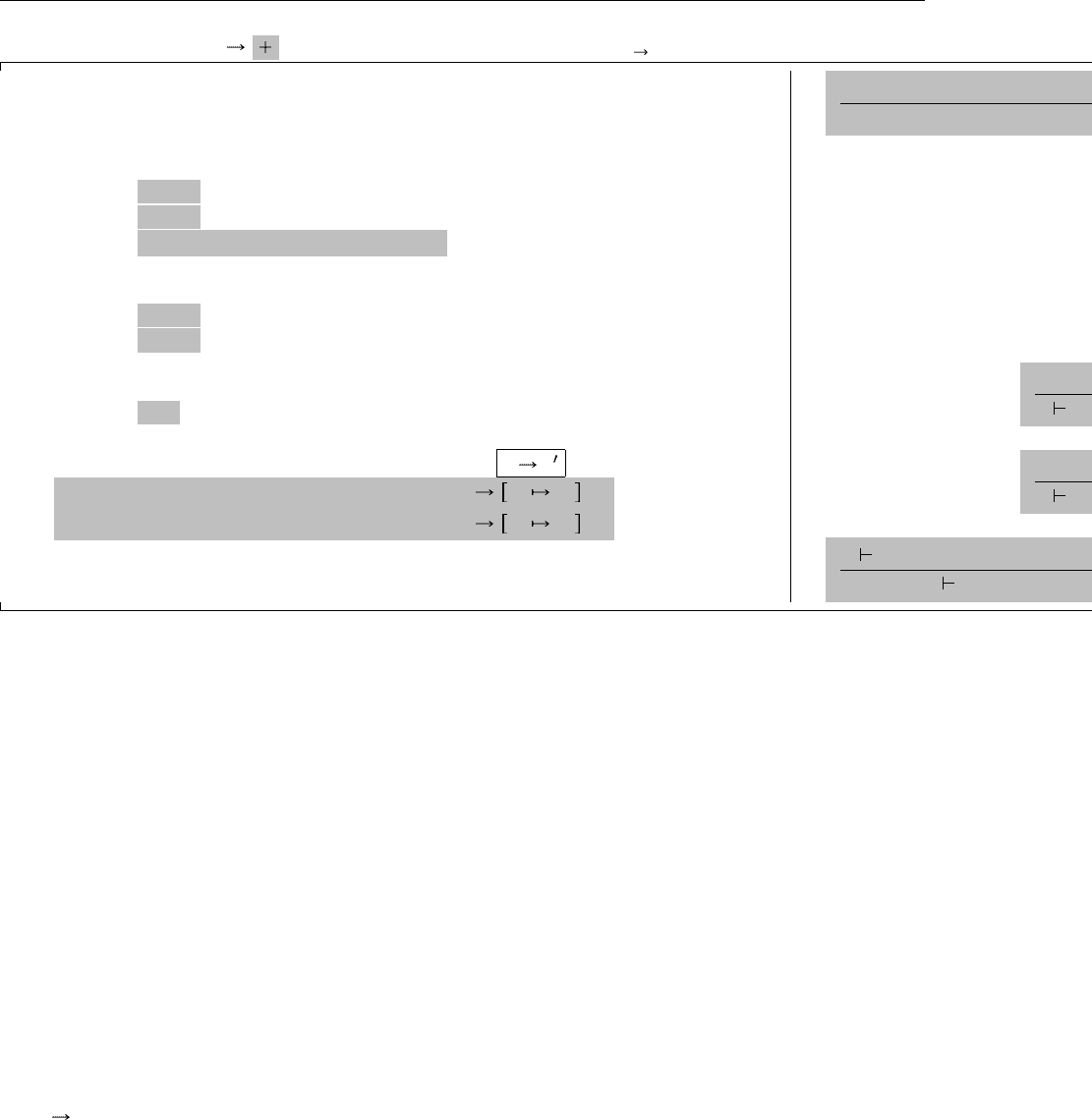
108 11.9. Типы-суммы
Расширяет λ (9.1)
Новые синтаксические формы
t ::= . . . термы:
inl t постановка тега (левого)
inr t постановка тега (правого)
case t of inl x=>t | inr x=>t case
v ::= . . . значения:
inl v значение с тегом (левым)
inr v значение с тегом (правым)
T ::= . . . типы:
T+T тип-сумма
Новые правила вычисления t t
case (inl v
0
) of inl x
1
=>t
1
| inr x
2
=>t
2
x
1
v
0
t
1
(E-CaseInl)
case (inr v
0
) of inl x
1
=>t
1
| inr x
2
=>t
2
x
2
v
0
t
2
(E-CaseInr)
t
0
t
0
case t
0
of inl x
1
=>t
1
| inr x
2
=>t
2
case t
0
of inl x
1
=>t
1
| inr x
2
=>t
2
(E-Case)
t
1
t
1
inl t
1
inl t
1
(E-Inl)
t
1
t
1
inr t
1
inr t
1
(E-Inr)
Новые правила типизации Γ t : T
Γ t
1
: T
1
Γ inl t
1
: T
1
+ T
2
(T-Inl)
Γ t
1
: T
2
Γ inr t
1
: T
1
+ T
2
(T-Inr)
Γ t
0
: T
1
+ T
2
Γ, x
1
:T
1
t
1
: T Γ, x
2
:T
2
t
2
: T
Γ case t
0
of inl x
1
=>t
1
| inr x
2
=>t
2
: T
(T-Case)
Рис. 11.9. Суммы
производящие «инъекцию» элементов ФизАдрес или ВиртАдрес в левую или правую компоненту типа-
суммы Адрес. Заметим, однако, что в в нашем формальном описании они функциями не являются.)
В общем случае, элементы типа T
1
+ T
2
состоят из элементов T
1
, снабженных тегом inl, и элементов
T
2
, снабженных тегом inr.
Для использования типов-сумм мы вводим конструкцию case, позволяющую нам различать, про-
исходит ли данное значение с левой или правой ветви суммы. Например, имя из значения типа Адрес
можно извлечь так:
получитьИмя
= $\ L$aАдрес:.
case a of
inl x = > xфио.
| inr y = > yимя.;
Когда в виде параметра a выступает ФизАдрес с тегом inl, выражение case выполнит первую ветвь
и свяжет переменную x со значением типа ФизАдрес; тело первой ветви извлекает из x поле фио и
возвращает его. Подобным образом, если a есть ВиртАдрес с тегом inr, будет выбрана вторая ветвь
и возвращено поле имя в значении типа ВиртАдрес. Таким образом, тип всей функции получитьИмя —
Адрес String.
Описанные нами конструкции формально представлены на Рис. 11.9. Мы добавляем левую и правую
инъекции, а также конструкцию case, к синтаксису термов; к типам мы добавляем конструктор суммы.
К правилам вычисления мы добавляем два варианта «бета-редукции» для конструкции case — один
для случая, когда первый подтерм сведен к значению v
0
с тегом inl, второй для значения v
0
с тегом inr.
В обоих случаях мы выбираем соответствующую ветвь и выполняем ее тело с подстановкой v
0
вместо
связанной переменной. Остальные правила вычисления проводят шаг в первом подтерме выражения
case либо внутри тегов inl или inr.
Правила типизации для тегов не представляют ничего сложного: чтобы показать, что inl t
1
имеет
rev. 104
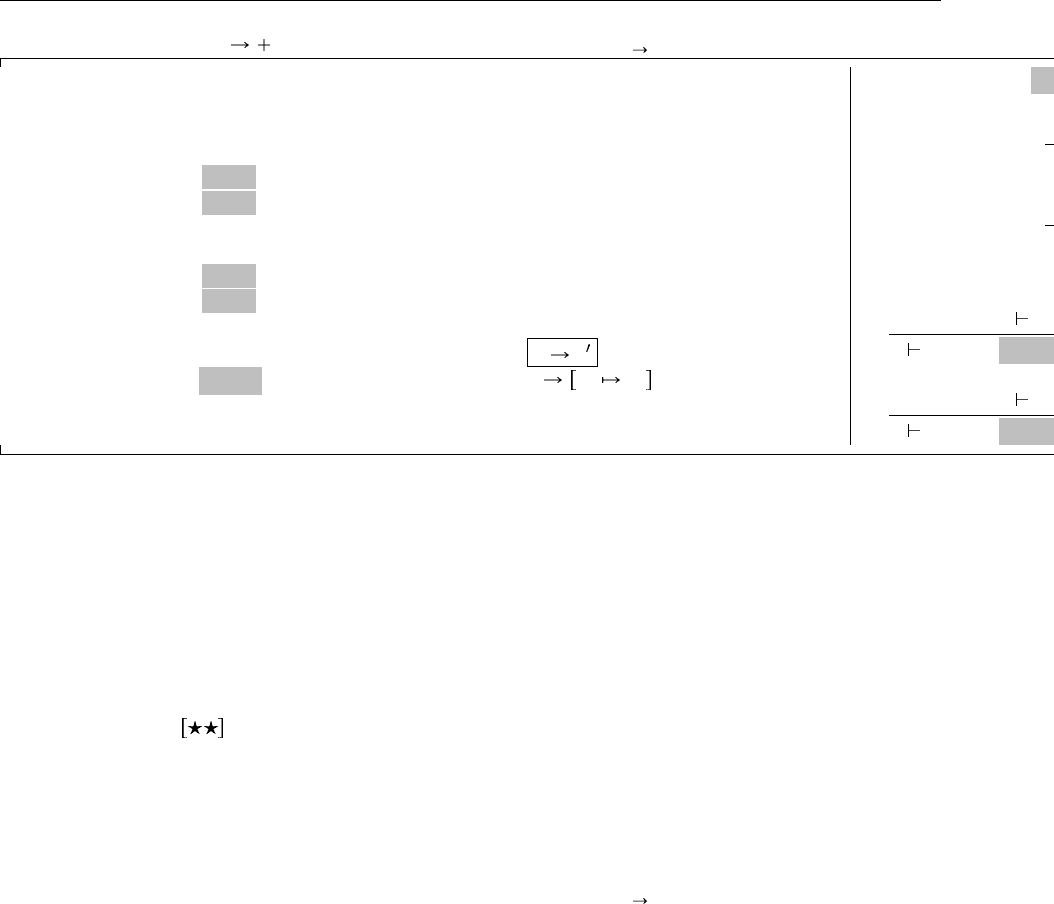
11.9. Типы-суммы 109
Расширяет λ (11.9)
Новые синтаксические формы
t ::= . . . термы:
inl t as T постановка тега (левого)
inr t as T постановка тега (правого)
v ::= . . . значения:
inl v as T значение с тегом (левым)
inr v as T значение с тегом (правым)
Новые правила вычисления t t
case (inl v
0
) as T
0
of inl x
1
=>t
1
| inr x
2
=>t
2
x
1
v
0
t
1
(E-CaseInl)
case (inr v
0
) as T
0
of inl x
1
=>t
1
| inr x
2
=>t
2
x
2
v
0
t
2
(E-CaseInr)
t
1
t
1
inl t
1
as T
2
inl t
1
as T
2
(E-Inl)
t
1
t
1
inr t
1
as T
2
inr t
1
as T
2
(E-Inr)
Новые правила типизации Γ t : T
Γ t
1
: T
1
Γ inl t
1
as T
1
+ T
2
: T
1
+ T
2
(T-Inl)
Γ t
1
: T
2
Γ inr t
1
as T
1
+ T
2
: T
1
+ T
2
(T-Inr)
Рис. 11.10. Суммы (с единственностью типизации)
тип-сумму T
1
+ T
2
, достаточно показать, что t
1
принадлежит первому суммируемому типу, T
1
, и точно
так же для inr. В случае конструкции case нам надо проверить, что первый подтерм имеет тип T
1
+ T
2
, а также что тела обеих ветвей t
1
и t
2
имеют один и тот же тип T. Следуя соглашениям из
предыдущих определений, Рис. 11.9 не утверждает явно, что область видимости переменных x
1
и x
2
ограничена телами ветвей t
1
и t
2
, но это можно понять по тому, как расширяются контексты в правиле
типизации T-Case.
Упражнение 11.9.1 : Обратите внимание на подобие между правилом типизации для case и
правилом для if на Рис. 8.1: можно рассматривать if как своего рода вырожденную форму case,
когда в ветви не передается никакая информация. Сделайте эту интуицию формальной, определив
true, false и if в виде производных форм на основе сумм и Unit.
11.9.1. Суммы и единственность типов
Большинство полезных свойств отношения типизации чистого λ (см. §9.3) сохраняются и в си-
стеме с типами-суммами, но одно важное свойство теряется: Теорема о единственности типов (9.3.3).
Сложность возникает из-за конструкций постановки тегов inl и inr. Например, правило типизации
T-Inl говорит, что, зная, что t
1
является элементом T
1
, мы можем вывести утверждение, что inl t
1
является элементом T
1
+ T
2
, для любого типа T
2
. Например, можно вывести inl 5 : Nat+Nat и inl
5 : Nat+Bool (и бесконечное число других типов). Несоблюдение единственности типов означает, что
невозможно построить алгоритм проверки типов путем «считывания правил снизу вверх», как мы это
делали для всех конструкций, рассмотренных до сих пор. Мы можем выбрать один из нескольких
вариантов:
1. Можно усложнить алгоритм проверки типов, чтобы он как-то «догадывался», какое значение T
2
требуется. А именно, можно сохранять T
2
неопределенным и пытаться впоследствии определить,
что за тип должен быть на этом месте. Такие методы будут подробно рассмотрены, когда мы
будем изучать реконструкцию типов (Глава 22).
2. Можно расширить язык типов и единообразно представлять все типы T
2
одновременно. Этот
вариант будет изучен в рамках разговора о наследовании (Глава 15).
3. Можно требовать, чтобы программист предоставлял явную аннотацию, указывая, какой тип T
2
имеется в виду. Эта альтернатива самая простая — и, на самом деле, не настолько непрактичная,
rev. 104
110 11.10. Варианты
как может показаться, поскольку в полноценных проектах языков явные аннотации часто можно
«прицепить» к другим конструкциям и сделать почти невидимыми (мы вернемся к этому вопросу
в следующем разделе). Пока что мы выбираем именно этот вариант.
На Рис. 11.10 показаны требуемые расширения языка по отношению к Рис. 11.9. Вместо простого
inl t или inr t мы пишем inl t as T или inr t as T, где T изображает целиком тот тип-сумму,
к которому мы намереваемся отнести снабженный тегом элемент. Правила типизации T-Inl и T-Inr
используют указанный тип-сумму как тип результата инъекции, проверяя предварительно, что терм,
подъвергаемый инъекции, действительно лежит на соответствующей ветви суммы (чтобы не повторять
в правилах T
1
+ T
2
по многу раз, синтаксические правила позволяют при инъекции указывать любой
тип как аннотацию. Правила типизации позаботятся о том, чтобы этот тип всегда был типом-суммой,
при условии, что инъекция правильно типизируется.) Синтаксис аннотаций типов устроен так, чтобы
напоминать конструкцию приписывания типов из §11.4: в сущности, эти аннотации можно рассматри-
вать как синтаксически обязательные приписывания типов.
11.10. Варианты
Бинарные типы-суммы являются частным случаем типов-вариантов с метками так же, как би-
нарные типы-произведения являются частным случаем записей с метками полей. Вместо T
1
+T
2
мы
будем писать <l
1
:T
1
, l
2
:T
2
>, где l
1
и l
2
— метки полей. Вместо inl t as T
1
+T
2
будем писать <l
1
=t>
as <l
1
:T
1
, l
2
:T
2
>. А вместо обозначений inl и inr в вариантах конструкции case мы будем исполь-
зовать те же метки, что и в соответствующем типе-сумме. С такими обобщениями пример функции
получитьИмя из предыдущего раздела начинает выглядеть так:
Адрес
= физическийФизАдрес <: , виртуальныйВиртАдрес: >;
a = физический <:pa > as Адрес;
a: АдресполучитьИмя
= λaАдрес:.
case a ofфизический
<=x > = > xфио.
| виртуальный <=y > = > yимя.;
получитьИмя : Адрес -> String
Формальное определение типов-вариантов приводится на Рис. 11.11. Обратите внимание, что, как и в
записях в §11.8, порядок меток в вариантном типе считается существенным.
11.10.1. Опции
Одна из весьма полезных идиом с использованием вариантов — опциональные значения. Например,
элементом типа
Optiona l N a t = <none : Unit , some : Nat >;
может быть либо тривиальное значение unit с тегом none, либо целое число с тегом some — другими
словами, тип OptionalNat изоморфен типу Nat с добавлением отдельного выделенного значения none.
Тип
Table = Nat - > Option a l N a t ;
представляет конечные отображения чисел в числа: областью определения такого отображения служит
множество входов, на которых результат имеет вид <some=n> для некоторого n. Пустая таблица
empt y T a b l e = $\ L$n : Nat . < none = unit > as OptionalNat ;
empt y T a b l e : Table
— это константная функция, возвращающая none в ответ на любое входное значение. Конструктор
rev. 104
