Пирс Б. Типы в языках программирования

Подождите немного. Документ загружается.

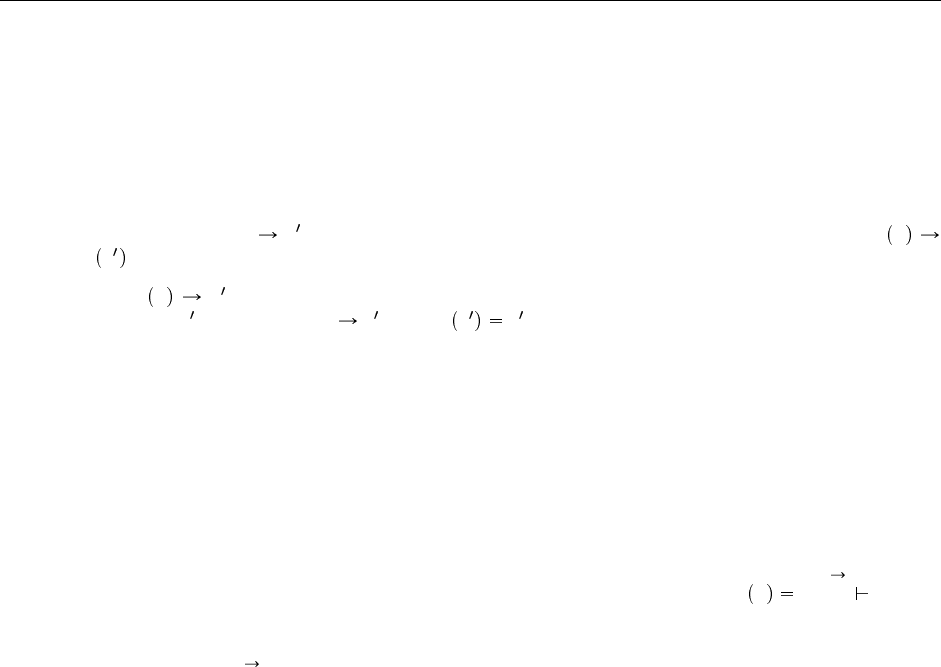
9.6. Стиль Карри и стиль Чёрча 91

Разумеется, мы ожидаем, что два способа представления семантики простого типизированного

лямбда-исчисления совпадут: не должно иметь значения, вычисляем ли мы типизированный терм на-

прямую, или проводим стирание типов и затем вычисляем получившийся бестиповый терм. Это наше

ожидание формализуется в следующей теореме, которая воплощает лозунг «вычисление коммутирует

со стиранием», в смысле, что эти операции можно проводить в любом порядке — вычислив, и потом сте-

рев типы, мы получаем тот же самый результат, как если бы сначала стерли типы, а потом вычислили

терм:

Теорема 9.5.2 1. Если t t согласно типизированному отношению вычисления, то erase t

erase t .

2. Если erase t m согласно бестиповому отношению вычисления, то существует типизиро-

ванный терм t , такой, что t t и erase t m .

Доказательство: Несложная индукция по деревьям вывода вычисления.

Поскольку рассматриваемая нами «компиляция» настолько проста, Теорема 9.5.2 очевида до три-

виальности. Однако для более интересных языков и более интересных компиляторов она становится

важным свойством: она утверждает, что «высокоуровневая» семантика, напрямую выраженная на язы-

ке, используемом программистом, совпадает с альтернативной низкоуровневой стратегией вычисления,

реально используемой в реализации языка.

Еще один интересный вопрос, связанный с функцией стирания, таков: если у нас есть бестиповый

терм m, можем ли мы найти простой типизированный терм t, дающий при стирании типов m?

Определение 9.5.3 Терм m бестипового лямбда-исчисления называется типизируемым в λ если име-

ется простой типизированный терм t типа T и контекст Γ, такой, что erase t m и Γ t : T.

К этому вопросу мы вернемя в Главе 22, когда рассмотрим близкородственную проблематику ре-

конструкции типов для λ .

9.6. Стиль Карри и стиль Чёрча

Как мы видели, семантику простого типизированного лямбда-исчисления можно определить двумя

способами: как отношение вычисления, определенное прямо на синтаксисе простого типизированного

исчисления, либо как компиляцию в бестиповое исчисление в сочетании с отношением вычисления на

бестиповых термах. Существенное общее свойство обоих стилей состоит в том, что можно говорить о

поведении терма t вне зависимости от того, правильно он типизирован или нет. Такая форма опреде-

ления языка называется стилем Карри. Сначала мы задаем грамматику термов, затем определяем их

поведение, и, наконец, добавляем систему типов, отвергающую некоторые термы, чье поведение нам не

нравится. Семантика возникает раньше типизации.

Существенно другой способ организации определения языка состоит в том, чтобы сначала опреде-

лить термы, затем выбрать из них правильно типизированные термы, и, наконец, определить семан-

тику только на них. В таких системах, называемых системами в стиле Чёрча, типизация идет прежде

семантики: невозможно даже задать вопрос «каково поведение неверно типизированного терма?». В

сущности, строго говоря, в системах, построенных по Чёрчу, мы вычисляем не термы, а деревья вывода

типов для них. (Пример можно найти в §15.6.)

Исторически сложилось, что неявно типизированные представления лямбда-исчислений часто опи-

сываются в стиле Карри, а представления Чёрча в основном встречаются для явно типизированных

систем. Отсюда происходит некотрая путаница в терминологии: иногда «стилем Чёрча» называют явно

типизированный синтаксис, а «стилем Карри» неявно типизированный.

9.7. Дополнительные замечания

Простое типизированное лямбда-исчисление изучается в книге Хиндли и Селдина (Hindley and

Seldin 1986), и, еще более подробно, в монографии Хиндли (Hindley 1997).

rev. 104

92 9.7. Дополнительные замечания

Правильно типизированные

программы не могут

«сломаться».

Робин Милнер (Milner 1978)

rev. 104

Глава 10

Реализация простых типов на ML

Конкретная реализация λ в виде программы на ML следует той же схеме, что и реализация

бестипового лямбда-исчисления в Главе 7. Основная новая деталь — функция typeof для вычисления

типа данного терма в данном контексте. Впрочем, прежде чем мы до нее доберемся, нам требуется

ввести несколько низкоуровневых процедур для работы с контекстами.

10.1. Контексты

Напомним (Глава 7, стр. 72), что контекст (context) представляет собой просто список имен пере-

менных и связываний:

type contex t = ( string * binding ) list

В Главе 7 контексты использовались исключительно для преобразования между именованной и безы-

мянной формами термов при их считывании и распечатке. Для этого нам было лостаточно знать толь-

ко имена переменных; binding определялся как тривиальный тип данных с одним конструктором, не

несущим никакой информации:

type bindin g = NameB ind

При реализации процедуры проверки типов нам понадобится использовать контекст для хранения

сведений о типах переменных. Ради этого мы добавляем к типу binding новый конструктор VarBind:

type bindin g =

Nam eBind

| VarBind of ty

Каждый экземпляр с конструктором VarBind содержит сведения о типе соответствующей переменной.

Мы сохраняем старый конструктор NameBind ради удобства функций чтения и распечатки, которым

сведения о типе не нужны. (При другой стратегии реализации можно было бы определить два различ-

ных типа context — один для чтения и распечатки, а другой для проверки типов.)

Функция typeof вызывает функцию addbinding, чтобы расширить контекст ctx новым связыва-

нием переменной (x,bind); поскольку контексты у нас представляются в виде списков, addbinding, в

сущности, работает просто как cons:

let addbinding ctx x bind = (x , bind ):: ctx

Функция getTypeFromContext, наоборот, используется для поиска сведений о типе, связанном с некото-

рой переменной i в контексте ctx (информация fi о позиции в файле служит для распечатки сообщения

об ошибке, когда i оказывается вне контекста):

Интерпретатор, описанный в этой главе, соответствует простому типизированному лямбда-исчислению (Рис. 9.1) с

булевскими значениями (8.1). Код из этой главы можно найти в репозитории под именем simplebool.

94 10.2. Термы и типы

let g e t Ty p e Fr o m C on t e xt fi ctx i =

match g e t b i nding fi ctx i with

Va rBind ( tyT ) -> tyT

| _ -> error fi

(" g e t T yp e F r om C o nt e x t :␣ Wrong ␣ kind ␣ of ␣ bindi ng ␣ for ␣ var iable ␣ "

^ ( index2 n a m e fi ctx i ))

Оператор match производит проверку на непротиворечивость: в нормальных условиях,

getTypeFromContext всегда должна вызываться, когда i-е связывание образовано конструктором

VarBind. Однако в последующих главах у нас будут другие типы связываний (в частности, связы-

вания для типовых переменных), и может случиться так, что getTypeFromContext будет вызвана

с переменной неправильного вида. В этом случае, она печатает сообщение об ошибке при помощи

низкоуровневой функции error, передавая ей info, чтобы та могла сообщить о позиции в файле, где

произошла ошибка.

val error : info -> string -> ’a

Тип результата функции error — типовая переменная ’a, и она может принимать значение любого

типа ML (что имеет смысл, так как error все равно никогда не возвращается: она печатает ошибку и

останавливает программу). В данном случае нам нужно предполагать, что результат error имеет тип

ty, так как именно его возвращает другая ветвь match.

Заметим: что информацию о типах мы ищем по индексу, поскольку внутри программы термы пред-

ставляются в безымянной форме, и переменные в них представляются числовыми индексами. Функция

getbinding ищет i-ое связывание в данном контексте:

val getbinding : info -> cont ext -> int -> bi nding

Ее определение можно найти в реализации simplebool на веб-сайте книги.

10.2. Термы и типы

Синтаксис типов прямо переводится из абстрактного синтаксиса на Рис. 8.1 и 9.1 в определение

ML-ского типа.

type ty =

Ty Bool

| TyArr of ty * ty

Представление термов такое же, как было у нас при реализации бестипового лямбда-исчисления

(стр. 71), только к варианту TmAbs добавляется аннотация типа.

type term =

Tm True of info

| TmFalse of info

| TmIf of info * term * term * term

| TmVar of info * int * int

| TmAbs of info * st ring * ty * term

| TmApp of info * term * term

10.3. Проверка типов

Функцию проверки типов typeof можно рассматривать как простой перевод правил типизации для

λ (Рис. 8.1 и 9.1), или, вернее, как перевод леммы об обращении (9.3.1). Второй способ описания

точнее, поскольку именно лемма об обращении говорит нам для каждой синтаксической формы, какие

условия должны выполняться, чтобы терм считался правильно типизированным. Правила типизации

говорят нам, что некоторые термы правильно типизированы при некоторых условиях, но при взгляде

на каждое конкретное правило типизации мы никогда не можем заключить, что некоторый терм не

типизирован правильно, поскольку всегда остается возможность, что для типизации терма достаточно

rev. 104

10.3. Проверка типов 95

применить какое-то другое правило. (Пока что может казаться, что разницы все равно никакой нет,

поскольку лемма об обращении непосредственно следует из правил типизации. Однако различие стано-

вится существенным в последующих системах, где для доказательства леммы об обращении требуется

больше работы, чем в λ .)

let rec type of ctx t =

match t with

Tm True ( fi ) ->

Ty Bool

| TmFalse ( fi ) ->

Ty Bool

| TmIf ( fi ,t1 , t2 , t3 ) ->

if (=) ( typeo f ctx t1 ) TyBool then

let tyT2 = typeof ctx t2 in

if (=) tyT2 ( typeof ctx t3 ) then tyT2

else err or fi " arms ␣ of ␣ conditio n a l ␣ have ␣ d i f ferent ␣ types "

else err or fi " guard ␣ of ␣ co n d i t i o n a l ␣ not ␣a ␣ b oolean "

| TmVar ( fi , i ,_) -> getT y p e Fr o m C on t e xt fi ctx i

| TmAbs ( fi , x , tyT1 , t2 ) ->

let ctx ’ = ad d b i n ding ctx x ( VarBin d ( tyT1 )) in

let tyT2 = typeof ctx ’ t2 in

TyArr ( tyT1 , tyT2 )

| TmApp ( fi , t1 , t2 ) ->

let tyT1 = typeof ctx t1 in

let tyT2 = typeof ctx t2 in

( match tyT1 with

TyArr ( tyT11 , tyT12 ) ->

if (=) tyT2 tyT11 then tyT12

else err or fi " par a meter ␣ type ␣ misma tch "

| _ -> error fi " arrow ␣ type ␣ ex p ected ")

Здесь полезно сделать несколько замечаний о языке OCaml. Во-первых, мы пишем OCaml-овскую

операцию проверки на равенство в скобках, потому что она используется в префиксной позиции, а не в

нормальной инфиксной. Это делается для того, чтобы легче было сравнивать наш код с последующими

версиями typeof, где операция сравнения типов будет более изощренной, чем простое сравнение. Во-

вторых, операция сравнения проверяет структурное равенство составных значений, а не равенство

указателей. А именно, выражение

let t = TmApp (t1 , t2 ) in

let t ’ = TmApp (t1 , t2 ) in

(=) t t ’

всегда возвращает true, несмотря на то, что два экземпляра TmApp, именуемые переменными t и t’,

порождаются в разное время и имеют разные адреса в памяти.

rev. 104

96 10.3. Проверка типов

rev. 104

Глава 11

Простые расширения

Простое типизированное лямбда-исчисление обладает достаточной структурой, чтобы его теорети-

ческие характеристики было интересно исследовать, но как язык программирования, само по себе, его

рассматривать нельзя. В этой главе мы начинаем покрывать разрыв с более привычными языками, и

добавляем к исчислению несколько хорошо знакомых конструкций, которые без труда можно описать

на уровне типов. Важной темой на протяжении всей главы являются производные формы.

11.1. Базовые типы

Всякий язык программирования предоставляет набор базовых типов — множеств простых, неструк-

турированных значений, например, числа, булевские значения или символы, — и соответствующие

элементарные операции для работы с этими значениями. Мы уже детально рассмотрели рассмотре-

ли натуральные числа и булевские значения; проектировщик языка без труда может добавить в него

столько дополнительных типов, сколько захочет.

Помимо Bool и Nat, в оставшейся части книги мы иногда будем для оживления примеров исполь-

зовать базовые типы String (строки, с элементами вроде "hello") и Float (числа с плавающей точкой,

с элементами вроде 3.14159).

В теоретических целях часто бывает удобно абстрагироваться от свойств конкретных базовых типов

и их операций, и вместо этого полагать, что язык снабжен некоторым множеством A неинтерпрети-

руемых, или неизвестных, базовых типов, для которых не определено вообще никаких элементарных

операций. Этого можно достигнуть, попросту включив A в множество типов (с метапеременной A, при-

нимающей значения из A), как показано на Рис. 11.1. Для базовых типов мы используем букву A, а не

B, чтобы избежать путаницы с символом B, с помощью которого мы указываем на присутствие булев-

ских значений в данной системе. Можно считать, что буква A отсылает к атомарным типам — это еще

одно имя, которое часто используют для базовых типов, поскольку с точки зрения системы типов, у

них нет никакой внутренней структуры. В качестве имен базовых типов мы будем употреблять A. B, C и

т. д. Заметим, что, как и ранее с именами переменных и именами типовых переменных, A используется

и как имя базового типа, и как метапеременная, принимающая базовые типы в качестве значений, и

что имеется в виду в каждом конкретном случае, следует понимать из контекста.

В этой главе рассматриваются различные расширения чистого типизированного лямбда-исчисления (Рис. 9.1). Соот-

ветствующий интерпретатор на OCaml, fullsimple, содержит все эти расширения.

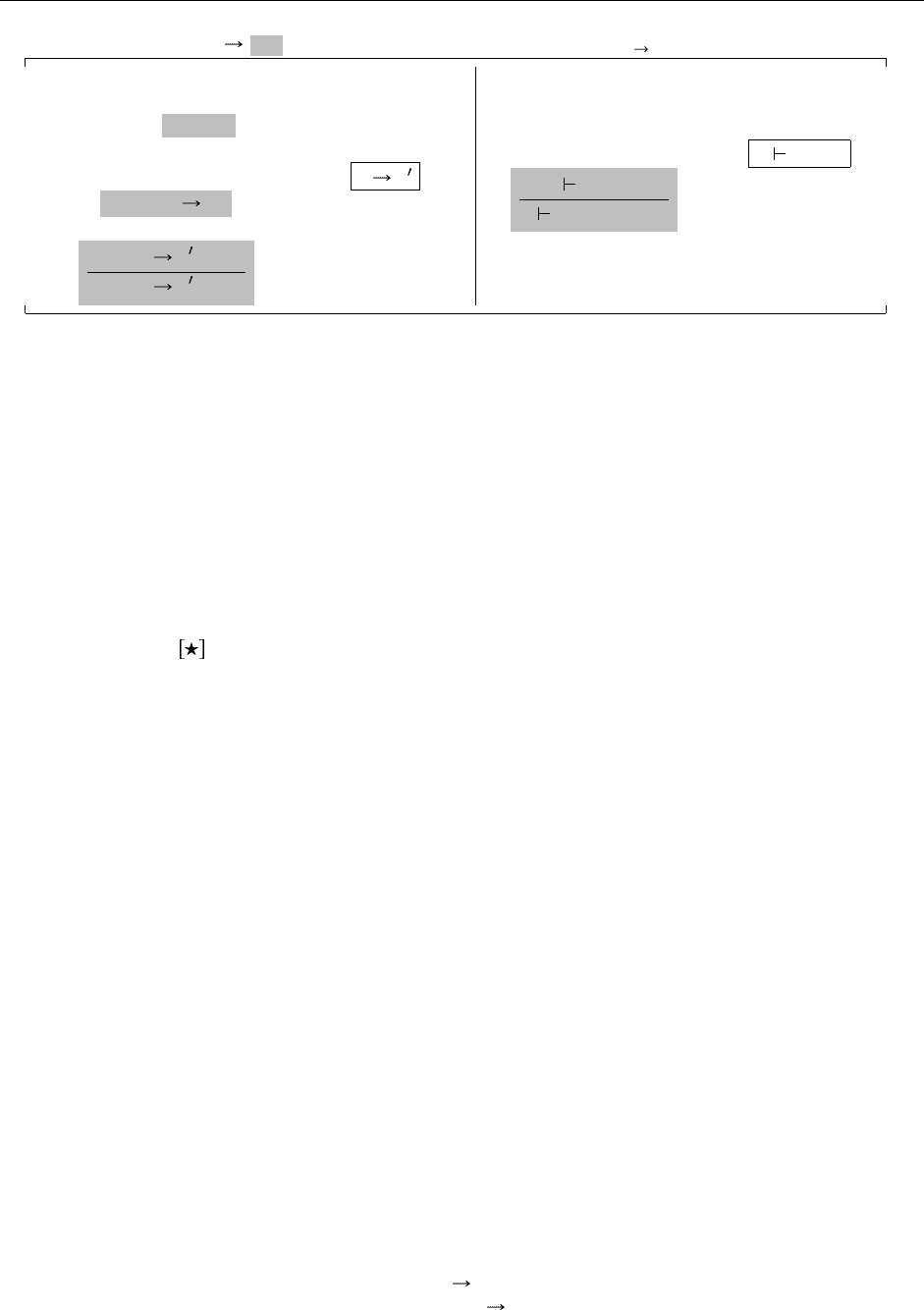
A Расширяет λ (9.1)

Новые синтаксические формы

T ::= . . . типы:

A базовый тип

Рис. 11.1. Неинтерпретируемые базовые типы

98 11.2. Единичный тип

Unit Расширяет λ (9.1)

Новые синтаксические формы

t ::= . . . термы:

unit константа unit

v ::= . . . значения:

unit константа unit

T ::= . . . типы:

Unit единичный тип

Новые правила типизации Γ t : T

Γ unit : Unit (T-Unit)

Новые производные формы

def

(λx:Unit.t

) t

где x F V t

Рис. 11.2. Единичный тип

Правда ли, что от неинтерпретируемого типа нет никакой пользы? Вовсе нет. Хотя мы никак не

можем прямо назвать его элементы, мы можем вводить переменные, принимающие значения этого

типа. Например, функция

λx :A. x;

<fun >: A -> A

— функция тождества для элементов A, каковы бы они ни были. Подобным образом,

λx :B. x;

<fun >: B -> B

— функция тождества для B, а

λf :A ->A , λx : A . f (f(x ));

<fun > : (A ->A ) -> A -> A

— функция, дважды производящая действие некоторой данной функции f над аргументом x.

11.2. Единичный тип

Еще один полезный базовый тип, встречающийся в основном в языках семейства ML — единичный

тип Unit, описанный на Рис. 11.2. В отличие от неинтерпретируемых базовых типов из предыдущего

раздела, этот тип интерпретируется наипростейшим возможным образом: мы явно вводим единствен-

ный его элемент, термовую константу unit (пишется с маленькой буквы u), и правило типизации,

делающее unit элементом Unit. Кроме того, мы добавляем unit к списку значений, могущих слу-

жить результатом вычисления: в сущности, unit — единственный возможный результат вычисления

выражения типа Unit.

Даже в чисто функциональном языке тип Unit не лишен некотрого интереса,

однако в основном

он применяется в языках с побочными эффектами, вроде присваивания ссылочным ячейкам — к этой

теме мы еще вернемся в Главе 13. В таких языках нас часто интересует в выражении не разультат

вычисления, а его побочный эффект; для подобных выражений Unit служит подходящим типом ре-

зультата.

Unit играет ту же роль, что тип void в языках вроде C и Java. Имя void наводит на мысли о пустом

типе Bot (см. §15.4), но используется он скорее как наш Unit.

Начиная с этого места, при выводе результатов вычислений мы будем экономить место и заменять тела λ-абстракций

на запись <fun>.

Мы надеемся, что читателям доставит удовольствие следующая небольшая загадка:

Упражнение 11.2.1 : Есть ли способ построить последовательность термов t

, t

, . . . на языке простого ти-

пизированного лямбда-исчисления с Unit в качестве единственного базового типа, так, чтобы для каждого n терм t

имел размер не более O n , но для достижения нормальной формы требовал по меньшей мере O 2

шагов вычисле-

ния?

rev. 104

11.3. Производные формы: последовательное исполнение и связывания-пустышки 99

11.3. Производные формы: последовательное исполнение и

связывания-пустышки

В языках с побочными эффектами часто бывает полезно вычислить два выражения одно за другим.

Конструкция последовательного исполнения t

; t

приводит к вычислению t

, игнорированию его

тривиального результата, и затем вычислению t

Формализовать последовательное исполнение можно двумя способами. Прежде всего, можно сле-

довать той же стратегии, что мы использовали для других синтаксических форм: добавить t

; t

качестве новой альтернативы к синтаксису термов, затем ввести два правила вычисления

; t

(E-Seq)

(E-SeqNext)

и правило типизации

Γ t

: Unit Γ t

: T

Γ t

; t

: T

(T-Seq)

и таким образом зафиксировать требуемое значение ;.

Альтернативный способ формализации последовательного исполнения состоит в том, чтобы рас-

сматривать t

; t

просто как сокращенную запись для терма (λx:Unit.t

) t

, где для переменной

x выбирается новое имя — то есть, такое, которое не совпадает ни с одной из свободных переменных

Интуитивно достаточно ясно, что с точки зрения программиста оба способа ввести последовательное

исполнение в язык приводят к одним и тем же результатам: высокоуровневые правила типизации и

вычисления можно вывести, если рассматривать t

; t

как сокращение для (λx:Unit.t

) t

. Это

соответствие можно доказать более формально, продемонстрировав, что и типизацию, и вычисление

можно «менять местами» с раскрытием сокращения.

Теорема 11.3.1 Последовательное испольнение как производная форма : Обозначим про-

стое типизированное лямбда-исчисление, дополненное типом Unit, конструкцией последовательного

исполнения и правилами E-Seq, E-SeqNext и T-Seq, символом λ

(где буква E взята из выраже-

ния external language, «внешний язык»), а простое типизированное лямбда-исчисление, куда добавлен

только тип Unit, обозначим символом λ

( internal language, «внутренний язык»). Пусть имеется

e λ

, функция раскрытия сокращений, которая переводит выражения внешнего языка на

внутренний, заменяя каждое вхождение конструкции t

; t

на (λx:Unit.t

) t

с новой перемен-

ной x. Тогда для каждого терма t языка λ

имеем

• t

t тогда и только тогда, когда e t

e t

• Γ

t : T тогда и только тогда, когда Γ

e t : T

где отношения вычисления и типизации языков λ

и λ

помечены, соответственно, символами E и

Доказательство: каждое направление в обоих “тогда и только тогда” доказывается с помощью пря-

молинейной индукции по структуре t.

Теорема 11.3.1 оправдывает применение термина производная форма, поскольку она показывает, что

поведение конструкции последовательного исполнения с точки зрения вычисления и типизации может

быть выведено на основе более базовых операций — абстракции и применения. Преимущество введения

конструкций вроде последовательного исполнения в виде производных форм состоит в том, что мы

таким образом расширяем внешний синтаксис (т. е., язык, реально используемый программистами при

написании программ), но при этом избегаем усложнения внутреннего языка, для которого нам нужно

доказывать теоремы вроде типовой безопасности. Такой метод борьбы со сложностью при описании

языковых конструкций можно найти уже в Сообщении об Алголе 60 (Naur et al. 1963), и он широко

применяется во многих более современных языковых описаниях, таких, как Определение Стандартного

ML (Milner, Tofte and Harper 1990; Milner, Tofte, Harper and MacQueen 1997).

rev. 104

100 11.4. Приписывание типа

as Расширяет λ (9.1)

Новые синтаксические формы

t ::= . . . термы:

t as T приписывание типа

Новые правила вычисления t t

as T v

(E-Ascribe)

t t

t as T t as T

(E-Ascribe1)

Новые правила типизации Γ t : T

Γ t

: T

Γ t

as T : T

(T-Ascribe)

Рис. 11.3. Приписывание типа

Часто производные формы называют синтаксическим сахаром, вслед за Ландином. Замена произ-

водной формы ее низкоуровневым определением называется удалением сахара.

Еще одна производная форма, которой мы часто будем пользоваться впоследствии — соглашение о

«связываниях-пустышках» в конструкциях, связывающих переменные. Часто бывает нужно (например,

в термах, создаваемых при удалении сахара из конструкций последовательного исполнения) записать

лямбда-абстракцию как «заглушку», где связываемая переменная нигде не встречается в теле. В таких

случаях бывает утомительно каждый раз придумывать новое имя; вместо этого мы будем заменять его

связыванием-пустышкой, которое выглядит как _. А именно, мы будем пользоваться записью λ_:S.t

в качестве сокращения λx:S.t, где x — некоторая переменная, не встречающаяся в t.

Упражнение 11.3.2 : Запишите правила вычисления и типизации для абстракций со связыванием-

пустышкой и докажите, что их можно вывести из правил расширения сокращений, приведенных

выше.

11.4. Приписывание типа

Еще одна простая конструкция, которая позднее часто будет нам помогать — явное приписыва-

ние определенного типа определенному терму (т. е., в программе явно записывается утверждение, что

данный терм имеет данный тип). Мы записываем «t as T», имея в виду «терм t, которому мы припи-

сываем тип T». Правило типизации T-Ascribe для этой конструкции (см. Рис. 11.3) просто-напросто

проверяет, что T и вправду является типом терма t. Правило вычисления E-Ascribe столь же очевид-

но: оно отбрасывает as-конструкцию, и t может после этого вычисляться обычным путем.

Приписывание типов может быть полезно в нескольких видах ситуаций. Часто оно служит для

документации. Иногда читателю бывает трудно уследить за типами всех подвыражений в сложном

составном выражении. Разумное использование явных приписываний типа может заметно облегчить

задачу. Подобным образом, в особенно больших выражениях даже автору может быть неясно, каковы

типы подвыражений. Приписывание типов нескольким из них может служить хорошим способоми

прояснить собственные мысли. И в самом деле, иногда явное приписывание типов помогает найти

источник трудноуловимых ошибок типизации.

Еще одно использование явного приписывания типов — управление распечаткой сложных типов.

Программы проверки типов, которыми протестированы примеры в этой книге, — а также вспомогатель-

ные интерпретаторы, чьи имена начинаются с full («полный»), — обладают простым механизмом для

введения сокращений вместо длинных выражений типов. (В остальных реализациях механизм сокра-

щений опущен, чтобы интерпретаторы легче было читать и модифицировать.) Например, объявление

UU = Unit -> Unit ;

превращает имя UU в сокращение для типа Unit Unit в оставшейся части программы. Где бы мы

ни встретили имя UU, его следует понимать как Unit Unit. Например, можно написать

rev. 104