Пирс Б. Типы в языках программирования

Подождите немного. Документ загружается.

5.3. Формальности 61

• Термы scc и prd представляют арифметические операции succ и pred, в том смысле, что, если

t является представлением числа n, то scc t дает при вычислении представление числа n + 1, а

prd t дает представление n - 1 (или 0, если n равно 0).

• Терм iszro представляет операцию iszero, в том смысле, что, если t является представлением 0,

то iszro t дает при вычислении true,

а если t представляет ненулевое число, то iszro t дает

false.

Собирая все эти утверждения вместе, представим, что у нас есть программа, которая проделывает

некоторые сложные численные вычисления и выдает булевский результат. Если мы заменим все чис-

ла и арифметические операции лямбда-термами, которые их представляют, и запустим получившуюся

программу, мы получим тот же самый результат. Таким образом, с точки зрения воздействия на оконча-

тельные результаты программ, нет никакой разницы между настоящими числами и их представлениями

по Чёрчу.

5.3. Формальности

В оставшейся части главы мы даем точное определение синтаксиса и операционной семантики

лямбда-исчисления. Большая часть необходимой структуры устроена так же, как в Главе 3 (чтобы

не повторять всю эту структуру заново, мы здесь определяем только чистое лямбда-исчисление, не до-

полненние булевскими значениями и числами). Однако операция подстановки терма вместо переменной

связана с неожиданными сложностями.

5.3.1. Синтаксис

Как и в Главе 3, абстрактная грамматика, определяющая термы (на стр. 63) должна рассматри-

ваться как сокращенная запись индуктивно определенного множества абстрактных синтаксических

деревьев.

Определение 5.3.1 Термы : Пусть имеется счетное множество имен переменных V. Множество

термов — это наименьшее множество T , такое, что

1. x T для всех x V;

2. Если t

T и x V, то λx.t

T ;

3. Если t

T и t

T , то t

T .

Размер терма t можно определить точно так же, как мы это сделали для арифметических вы-

ражений в Определении 3.3.2. Кроме того, можно дать простое индуктивное определение множества

свободных переменных, встречающихся в терме.

Определение 5.3.2 Множество свободных переменных терма t (записывается F V t ) определяется

так:

F V x x

F V λx. t

F V t

Упражнение 5.3.3 : Постройте строгое доказательство утверждения: F V t size t для лю-

бого терма t.

Строго говоря, по нашему определению, iszro t дает представление true в виде терма, но давайте, для простоты,

забудем сейчас про это различие. Можно аналогичным образом выстроить объяснение, как именно Чёрчевы булевские

константы представляют настоящие значения.

rev. 104

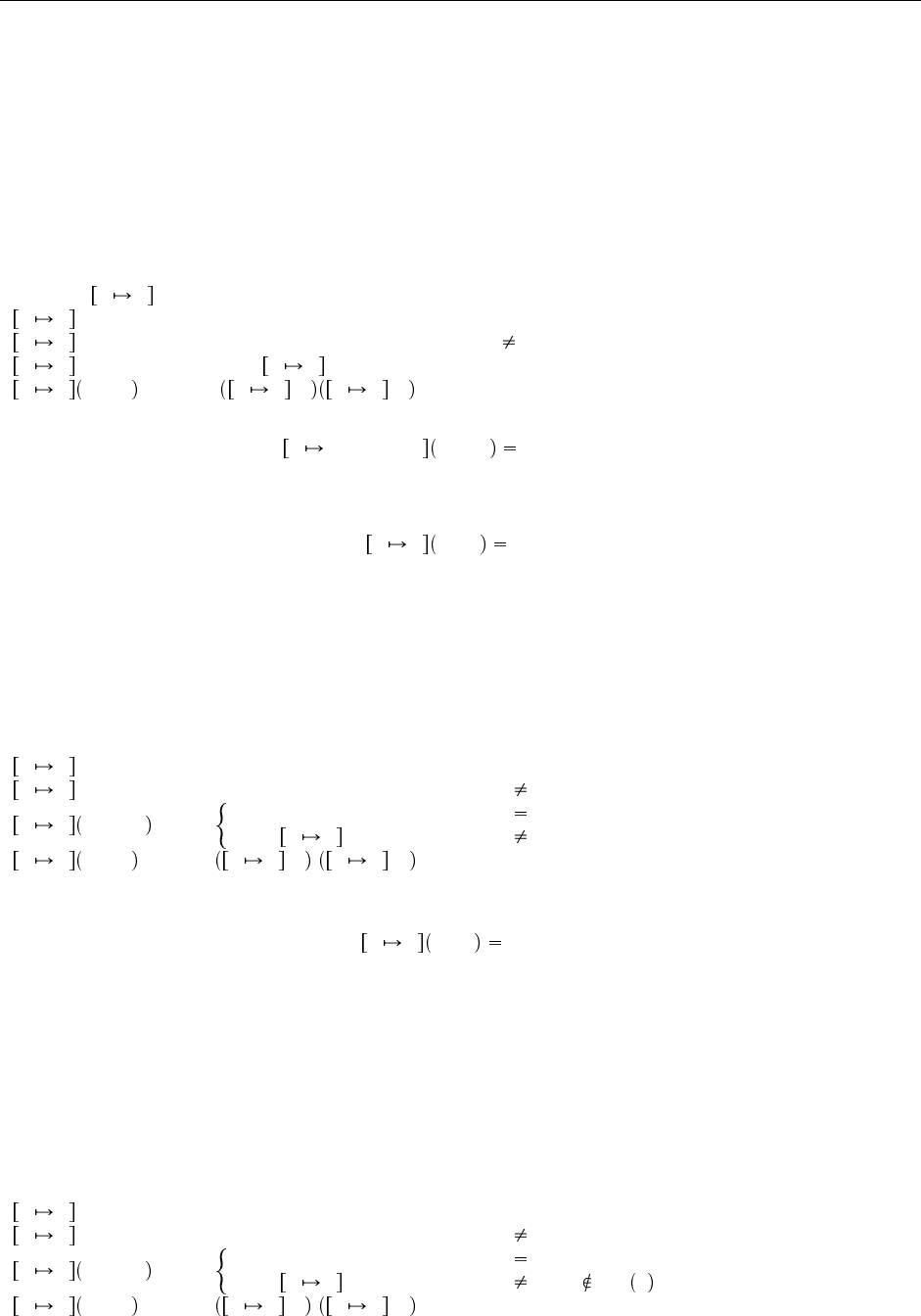
62 5.3. Формальности

5.3.2. Подстановка

Операция подстановки, когда ее требуется строго определить, оказывается довольно хитроумной. В

этой книге мы будем использовать два разных определения, каждое из которых удобно для своих целей.

Первое, вводимое нами в этом разделе, краткое и интуитивно понятное, хорошо работает в примерах,

в математических определениях и доказательствах. Второе, рассматриваемое в Главе 6, использует

более сложную нотацию и зависит от альтернативного «представления де Брауна» для термов, где

именованные переменные заменяются на числовые индексы, но оно оказывается более удобным для

конкретных реализаций ML, которые обсуждаются в последующих главах.

Поучительно придти к определению подстановки, пройдя через пару неудачных попыток. Попро-

буем сначала самое наивное рекурсивное определение. (С формальной точки зрения, мы определяем

функцию x s индукцией по аргументу t.):

x s x = s

x s y = y если y x

x s (λy. t

) = λy. x s t

x s t

= x s t

x s t

Такое определение в большинстве случаев работает правильно. Например, оно дает

x (λz. z w) λy. x λy. λz. z w

что соответствует нашей интуиции о том, как должна себя вести подстановка. Однако при неудачном

выборе имен связанных переменных это определение ломается. Например:

x y λx.x λx.y

Это противоречит базовой интуиции по поводу функциональной абстракции: имена связанных пере-

менных не должны ни на что влиять — функция тождества остается собой, запишем мы ее в виде

λx.x, λy.y или λfranz.franz. Если эти термы ведут себя по-разному при подстановке, они себя по-

разному поведут и при редукции, а это кажется неправильным.

Ясно, что первая ошибка, которую мы допустили при наивном определениии подстановки, состоит

в том, что мы не стали отличать свободное вхождение переменной x в терм t (которое при подстановке

нужно заменять) от связанного (которое не нужно). Когда мы достигаем абстракции, связывающей

имя x внутри t, операция подстановки должна останавливаться. Это ведет к следующей попытке:

x s x = s

x s y = y если y x

x s λy. t

λy. t

λy. x s t

если y x

x s t

= x s t

x s t

Такой вариант работает лучше, но, опять-таки, не всегда. Посмотрим, например, что получается, когда

мы пытаемся подставить терм z вместо переменной x в терме λz.x:

x z λz.x λz. z

В этот раз мы совершили, в сущности, противоположную ошибку: превратили функцию-константу λz.

x в функцию тождества! Это снова случилось оттого, что мы выбрали z в качестве имени связанной

переменной в функции-константе, так что что-то мы до сих пор делаем не так.

Ситуация, когда свободные переменные терма s становятся связанными, будучи наивно подстав-

ленными в терм t, называется захват переменных. Чтобы избежать его, нужно убедиться, что имена

связанных переменных в t отличаются от имен свободных переменных в s. Операция подстановки,

которая этого умеет правильно добиваться, называется подстановка, свободная от захвата. (Обычно,

когда просто говорят «подстановка», именно такую подстановку и имеют в виду.) Мы можем добиться

требуемого эффекта, если добавим еще одно условие ко второму варианту при подстановке в терм-

абстракцию:

x s x = s

x s y = y если y x

x s λy. t

λy. t

λy. x s t

если y x

если y x и y F V s

x s t

= x s t

x s t

rev. 104

5.4. Операционная семантика 63

(бестиповое)

Синтаксис

t ::= термы:

x переменная

λx.t абстракция

t t применение

v ::= значения:

λx.t значение-абстракция

Вычисление t t

(E-App1)

(E-App2)

(λx.t

) v

x v

(E-AppAbs)

Рис. 5.3. Бестиповое лямбда-исчисление (λ)

Теперь почти все правильно: наше определение подстановки делает то, что требуется, когда оно вообще

что-то делает. Проблема в том, что последнее изменение превратило подстановку из полной функции

в частичную. Например, новое определение не выдает никакого результата для x y z λy. x y :

связанная переменная y терма, в который производится подстановка, не равна x, но она встречается

как свободная в терме (y z), и ни одна строка определения не применима.

Распространенное решение этой проблемы в литературе по системам типов и лямбда-исчислению

состоит в том, что термы рассматриваются «с точностью до переименования переменных». (Чёрч назы-

вал операцию последовательного переименования переменных в терме альфа-конверсией. Этот термин

употребляется и до сих пор — мы могли бы сказать, что рассматриваем термы «с точностью до альфа-

конверсии».)

Соглашение 5.3.4 Термы, отличающиеся только именами связанных переменных, взаимозаменимы

во всех контекстах.

На пракике это означает, что имя любой λ-связанной переменной можно заменить на другое (после-

довательно проведя это переименование в теле λ) всегда, когда это оказывается удобным. Например,

если мы хотим вычислить x y z λy. x y , мы сначала переписываем (λy. x y) в виде, скажем,

(λw. x w). Затем мы вычисляем x y z λw. x w , что дает нам (λw. y z w).

Это соглашение делает наше определение «все равно что полным», поскольку каждый раз, как мы

пытаемся его применить к аргументам, к которым оно неприменимо, мы можем исправить дело пе-

реименованием, так, чтобы все условия выполнялись. В сущности, приняв это соглашение, мы можем

сформулировать определение подстановки чуть короче. Мы можем отбросить первый вариант в опреде-

лении для абстракций, поскольку всегда можно предположить (применяя, если надо, переименование),

что связанная переменная y отличается как от x, так и от свободных переменных s. Определение при-

нимает окончательный вид.

Определение 5.3.5 Подстановка :

x s x = s

x s y = y если y x

x s λy. t

= λy. x s t

если y x и y F V s

x s t

= x s t

x s t

5.4. Операционная семантика

Операционная семантика лямбда-термов вкратце представлена на Рис. 5.3. Множество значений

в этом исчислении более интересно, чем было в случае арифметических выражений. Поскольку вы-

числение (с вызовом по значению) останавливается, когда достигает лямбды, значениями являются

произвольные лямбда-термы.

rev. 104

64 5.5. Дополнительные замечания

Отношение вычисления показано в правом столбце рисунка. Как и в случае арифметических вы-

ражений, имеется два типа правил: рабочее правило E-AppAbs и правила соответствия E-App1 и

E-App2.

Обратите внимание, как выбор метапеременных в этих правилах помогает управлять порядком

вычислений. Поскольку v

может относиться только к значениям, левая сторона правила E-AppAbs

соотвтествует всем применениям термов, где терм-аргумент является значением. Точно так же, E-App1

относится к тем применениям, где левая часть не является значением, поскольку t

может обозначать

любой терм, но предпосылка правила требует, чтобы t

был способен совершить шаг вычисления. На-

против, E-App2 не срабатывает, пока левая часть не станет значением, которое может быть обозначено

метапеременной v. Взятые вместе, эти правила полностью определяют порядок вычисления терма вида

): сначала работает E-App1, пока t

не сведется к значению, затем E-App2 применяется до тех

пор, пока значением не окажется t

, и, наконец, само применение обрабатывается правилом E-AppAbs.

Упражнение 5.4.1 :

Модифицируйте эти правила, чтобы описать три другие стратегии вычисления: полную бета-

редукцию, нормальный порядок и ленивое вычисление.

Заметим, что в чистом лямбда-исчислении единственные возможные значения — это лямбда-

абстракции, так что, если E-App1 доводит t

до значения, это значение должно быть лямбда-

абстракцией. Разумеется, это утверждение перестает работать, как только мы добавляем в язык другие

конструкции, скажем, элементарные булевские значения, поскольку при этом у нас появляются новые

виды значений.

Упражнение 5.4.2 , :

В Упражнении 3.5.16 дается альтернативное представление операционной семантики булевских и

арифметических выражений, где тупиковые термы дают при вычислении особую константу wrong.

Распространите эту семантику на λNB.

Упражнение 5.4.3 :

В Упражнении 3.5.17 вводится стиль вычисления арифметических выражений «с большим шагом»,

где базовое отношение вычисления означает «терм t при вычислении дает окончательный результат

v». Покажите, как сформулировать правила вычисления лямбда-термов в этом стиле.

5.5. Дополнительные замечания

Бестиповое лямбда-исчисление было разработано Чёрчем и его коллегами в 20-е и 30-е годы (Church

1941). Стандартный текст по всем вопросам бестипового лямбда-исчисления – книга Барендрегта

(Barenddregt 1984); Хиндли и Селдин (Hindley and Seldin 1986) уже по охвату, но легче для чтения.

Статья Барендрегта (Barendregt 1990) в Справочнике по теоретической информатике представляет

собой краткий обзор. Сведения о лямбда-исчислении можно найти также во множестве учебников по

функциональным языкам программирования (Abelson and Sussman 1985; Friedman, Wand and Haynes

2001; Peyton Jones and Lester 1992) и по семантике языков программирования (напр., Schmidt 1986;

Gunter 1992; Winskel 1993; Mitchell 1996). Систематический метод кодирования различных структур

данных в виде лямбда-термов описан в статье Бёма и Берардуччи (B¨ohm and Berarducci 1985).

Несмотря на название, Карри не признавал за собой чести быть изобретателем каррирования. Часто

ее приписывают Шёнфинкелю (Sch¨onﬁnkel 1924), однако основная идея была уже известна нескольким

математикам 19-го века, включая Фреге и Кантора.

Возможно, у системы найдутся

приложения не только в роли

логического исчисления.

Алонсо Чёрч, 1932

rev. 104

Глава 6

Представление термов без

использованиия имен

В предыдущей главе мы работали с термами «с точностью до переименования связанных пере-

менных». У нас действовало общее соглашение, что связанные переменные можно в любой момент

переименовать, чтобы провести подстановку или если новое имя по каким-то другим причинам ока-

зывается удобнее. В сущности, «внешний вид» имени связанной переменной можно задать какой нам

понравится. Такое соглашение отлично работает при обсуждении основных идей лямбда-исчисления,

оно помогает понятно записывать доказательства, однако при реализации исчисления в виде програм-

мы нам нужно иметь для каждого терма единое представление; в частности, требуется решить, как

будут представлены вхождения переменных. Есть несколько способов решить эту задачу:

1. Можно представлять переменные символически, как мы это до сих пор делали, но заменить со-

глашение о молчаливом переименовании операцией, которая явным образом заменяет при под-

становке связанные переменные «свежими» именами по необходимости, чтобы избежать захвата.

2. Можно представлять переменные символически, но ввести общее условие, что имена всех связан-

ных переменных должны отличаться друг от друга и от всех где-либо встречающихся свободных

переменных. Такое соглашение (иногда его называют соглашение Барендрегта) более строго, чем

наше, поскольку не разрешается «на ходу» переименовывать переменные когда угодно. Однако это

правило не безопасно относительно подстановки (или бета-редукции): поскольку подставляемый

терм копируется, нетрудно построить примеры, где в результате подстановки получается терм

с одинаковыи именами у нескольких λ-абстракций. Следовательно, после каждого шага вычис-

ления, включающего подстановку, должен следовать шаг переименования, восстанавливающий

инвариант.

3. Можно сконструировать «каноническое» представление переменных и термов, при котором пере-

именование не нужно.

4. Можно вообще избежать понятия подстановки с помощью механизмов вроде явных подстановок

(Abadi, Cardelli, Curien and L´evy, 1991a).

5. Можно избежать переменных, если работать в языке, основанном на комбинаторах, например,

комбинаторной логике (Curry and Feys 1958; Barendregt 1984) — варианте лямбда-исчисления, где

вместо процедурной абстракции используются комбинаторы, — или на языке Бэкуса FP (Backus

1978).

Каждая из этих схем имеет свои преимущества, и выбор между ними до некоторой степени дело вкуса

(в серьезных реализациях компиляторов действуют еще соображения производительности, но нас они

В этой главе изучается бестиповое лямбда-исчисление, λ (Рис. 5.3). Соответствующая реализация на OCaml называ-

ется fulluntyped.

66 6.1. Термы и контексты

сейчас не волнуют). Мы выбираем третий вариант, который, по нашему опыту, будет лучше масшта-

бироваться, когда нам потребуется работать с некоторыми более сложными интерпретаторами из этой

книги. Одна из причин этого в том, что, будучи реализован с ошибками, он обычно завершается аварий-

но, а не выдает неверные ответы. Это позволяет нам обнаруживать и исправлять ошибки достаточно

быстро. Напротив, известны случаи, когда в реализациях, основанных на именованных переменных,

неправильное поведение длилось месяцы и годы. Наша реализация использует хорошо известный метод,

изобретенный Николасом де Брауном (de Bruijn 1972).

6.1. Термы и контексты

Идея де Брауна состояла в том, чтобы представлять термы более естественным — пусть и менее

читабельным, — образом, заставив вхождения переменных прямо указывать на их связывающие опре-

деления, всесто того, чтобы называть их по имени. Для этого можно заменить именованные переменные

натуральными числами, где число k означает «переменная, связанная k-й охватывающей λ». Напри-

мер, обыкновенный терм λx.x соответствует безымянному терму λ.0, а λx.λy. x (y x) соответствует

λ.λ. 1 (0 1). Безымянные термы иногда еще называют термами де Брауна, а нумерованные пере-

менные в них называются индексами де Брауна.

Разработчики компиляторов для того же понятия

используют термин «статические расстояния».

Упражнение 6.1.1 : Для каждого из следующих комбинаторов

= λs. λz . z ;

= λs. λz . s ( s z );

plus = λm . λn . λs. λz. m s (n s z );

fix = λf . (λx. f(λy . ( x x ) y )) (λx. f(λy . ( x x ) y ));

foo = (λx . (λx. x )) (λx . x );

запишите соответствующий безымянный терм.

Формально мы определяем синтаксис безымянных термов почти так же, как определялся синтаксис

обыкновенных термов (5.3.1). Единственная разница состоит в том, что требуется внимательно следить,

сколько свободных переменных может содержать каждый терм. То есть, требуется отличать множества

термов без свободных переменных (называемых 0-термами), термов, где максимум одна свободная

переменная (1-термы), и так далее.

Определение 6.1.2 Термы : Пусть T — наименьшее семейство множеств T

, T

, . . . , такое,

что

1. k T

, если 0 k n;

2. если t

и n 0, то λ.t

n 1

;

3. если t

и t

, то (t

) T

(Заметим, что мы имеем здесь стандартное индуктивное определение, только определяем семейство

множеств, индексируемое числами, а не одно множество.) Элементы каждого T

называются n-

термами.

Элементы T

— это термы с не более, чем n переменных, пронумерованных от 0 до n 1: каждый

данный элемент T

не обязан содержать свободные переменные со всеми этими номерами, и вообще не

обязан иметь какие-либо свободные переменные. В частности, если t замкнут, он является элементом

для любого n.

Заметим, что всякий (замкнутый) обыкновенный терм имеет ровно одно представление де Брауна,

и что два обыкновенных терма эквивалентны с точностью до переименования связанных переменных

тогда и только тогда, когда у них одинаковые представления де Брауна.

Фамилия de Bruijn читается «де Браун». В русскоязычной литературе встречаются варианты транслитерации «де

Брейн», «де Брюйн» и «де Бройн». — прим. перев.

rev. 104

6.1. Термы и контексты 67

Чтобы работать с термами, содержащими свободные переменные, нам потребуется понятие контек-

ста именования. Например, допустим, нам нужно представить в виде безымянного терма λx. y x. Мы

знаем, что делать с x, но не знаем, как вести себя с y, поскольку неизвестно, как «далеко» эта пере-

менная будет определена, и какой ей сопоставить номер. Решение состоит в том, чтобы выбрать, раз

и навсегда, присвоение (называемое контекстом именования) индексов де Брауна свободным перемен-

ным, и последовательно использовать это присвоение, когда требуется выбрать номер для свободной

переменной. Например, предположим, что мы решили работать в следующем контексте именования:

Γ x 4

y 3

z 2

a 1

b 0

Тогда x (y z) будет представлен как 4 (3 2), в то время как λw. y w будет представлен как λ. 4 0,

а λw.λa.x как λ.λ.6.

Поскольку порядок, в котором переменные следуют в Γ, однозначно определяет их числовые ин-

дексы, мы можем кратко записать контекст в виде последовательности.

Определение 6.1.3 Допустим, x

, . . . x

— имена переменных из V. Контекст именования Γ

, x

n 1

, . . . x

, x

присваивает каждой x

индекс де Брауна i. Заметим, что самая правая переменная

в контексте получает индекс 0; это соответствует тому, как мы считаем λ-связывания — справа

налево, — когда преобразуем именованный терм в безымянный. Множество x

, . . . , x

переменных,

упомянутых в Γ, мы обозначаем dom Γ .

Упражнение 6.1.4 , : Постройте альтернативную конструкцию множеств n-термов в сти-

ле Определения 3.2.3, и покажите (как в Утверждении 3.2.6), что ваше определение эквивалентно

имеющемуся.

Упражнение 6.1.5 Рекомендуется, :

1. Определите функцию removenames

t , которая принимает контекст именования Γ и обыкно-

венный терм t (где F V t dom Γ ), и порождает соответствующий безымянный терм.

2. Определите функцию restorenames

t , которая принимает безымянный терм t и контекст Γ,

и порождает обыкновенный терм. (В процессе вам придется «выдумывать» имена переменных,

связанных абстракциями в t. Можете предположить, что имена в V попарно различаются,

и что множество имен переменных V упорядочено, так что имеет смысл говорить «возьмем

первое имя переменной, которое еще не содержится в dom Γ ».)

Эта пара функций должна иметь свойство

removenames

restorenames

t t

для всякого безымянного терма t, а также

restorenames

removenames

t t

с точностью до переименования связанных переменных, для всякого обыкновенного терма t.

Строго говоря, нельзя говорить о «каком-то t T » — всегда нужно указывать, сколько свободных

переменных t разрешено иметь. На практике, впрочем, у нас всегда будет в распоряжении некоторый

заранее заданный контекст именования Γ; мы будем несколько вольно обращаться с нотацией и писать

t T , имея в виду t T

, где n – длина Γ.

rev. 104

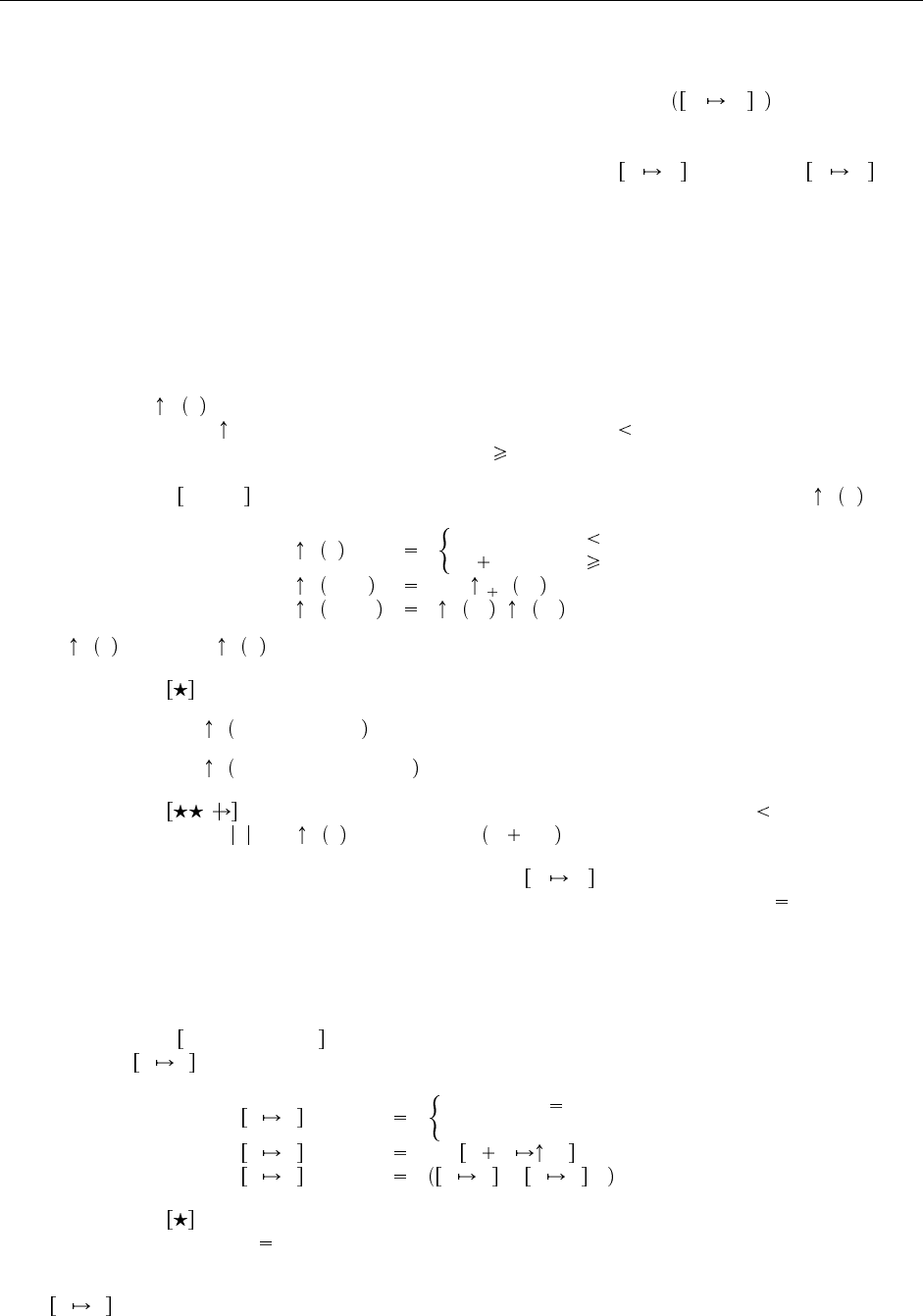
68 6.2. Сдвиг и подстановка

6.2. Сдвиг и подстановка

Нашей следующей задачей будет определить операцию подстановки k s t на безымянных

термах. Для этого потребуется вспомогательная операция, называемая «сдвиг», перенумеровывающая

индексы свободных переменных в терме.

Когда подстановка проникает внутрь λ-абстракции, к примеру, 1 s (λ.2) (т. е., t s λy.x,

если предположить, что 1 – индекс переменной x во внешнем контексте), контекст, в котором проис-

ходит подстановка, становится на одну переменную длиннее исходного; требуется увеличить индексы

свободных переменных в s, чтобы в новом контексте они ссылались на те же переменные, что и раньше.

Однако делать это нужно осторожно: нельзя просто увеличить на единицу все индексы переменных s,

потому что при этом сдвинулись бы и связанные переменные внутри s. Например, пусть s = 2 (λ.0)

(т. е., s = z (λw.w), если 2 — индекс z во внешнем контексте). В этом случае нам требуется сдвинуть

2, но не 0. Функция сдвига, описанная ниже, принимает параметр «отсечения» c, управляющий тем,

какие переменные сдвигаются. Он может быть 0 (что означает, что сдвигать надо все переменные),

и увеличивается каждый раз, когда функция сдвига пересекает границу абстракции. Таким образом,

при вычислении

t мы знаем, что терм t происходит изнутри c слоев абстракции по отношению

к исходному аргументу

. Получается, что все идентификаторы k c внутри t связаны в исходном

аргументе и сдвигу не подлежат, а идентификаторы k c свободны, и их нужно сдвинуть.

Определение 6.2.1 Сдвиг : Сдвиг терма t на d позиций с отсечением c, обозначаемый

t , опре-

деляется так:

k если k c

k d если k c

λ.t

λ.

c 1

Запись

t означает

t .

Упражнение 6.2.2 :

1. Чему равняется

λ.λ. 1 (0 2) ?

2. Чему равняется

λ. 0 1 (λ. 0 1 2) ?

Упражнение 6.2.3 , : Покажите, что, если t является n-термом и, если d 0, все свободные

переменные t не меньше d , то

t является max n d, 0 -термом.

Теперь мы готовы определить оператор подстановки j s t. Когда мы используем подстанов-

ку, обычно нас интересует подстановка последней переменной в контексте (т. е., j 0), поскольку

именно этот случай нам нужен, чтобы определить операцию бета-редукции. Однако для того, чтобы

подставить значение переменной 0 в терме, который является лямбда-абстракцией, требуется уметь

подставить значение переменной 1 в теле этой абстракции. Таким образом, определение подстановки

должно работать с произвольной переменной.

Определение 6.2.4 Подстановка :Подстановка терма s вместо переменной номер j в терме t, что

записывается j s t, определяется следующим образом:

j s k

s если k j

k в противном случае

j s (λ.t

) λ. j 1

s t

j s (t

) j s t

j s t

Упражнение 6.2.5 : Переведите следующие примеры подстановок в безымянную форму, предпола-

гая глобальный контекст Γ a, b, и вычислите результаты подстановки по Определению 6.2.4. Со-

ответствуют ли ответы исходному определению подстановки на обыкновенных термах из §5.3.5?

1. b a (b (λx.λy.b))

rev. 104

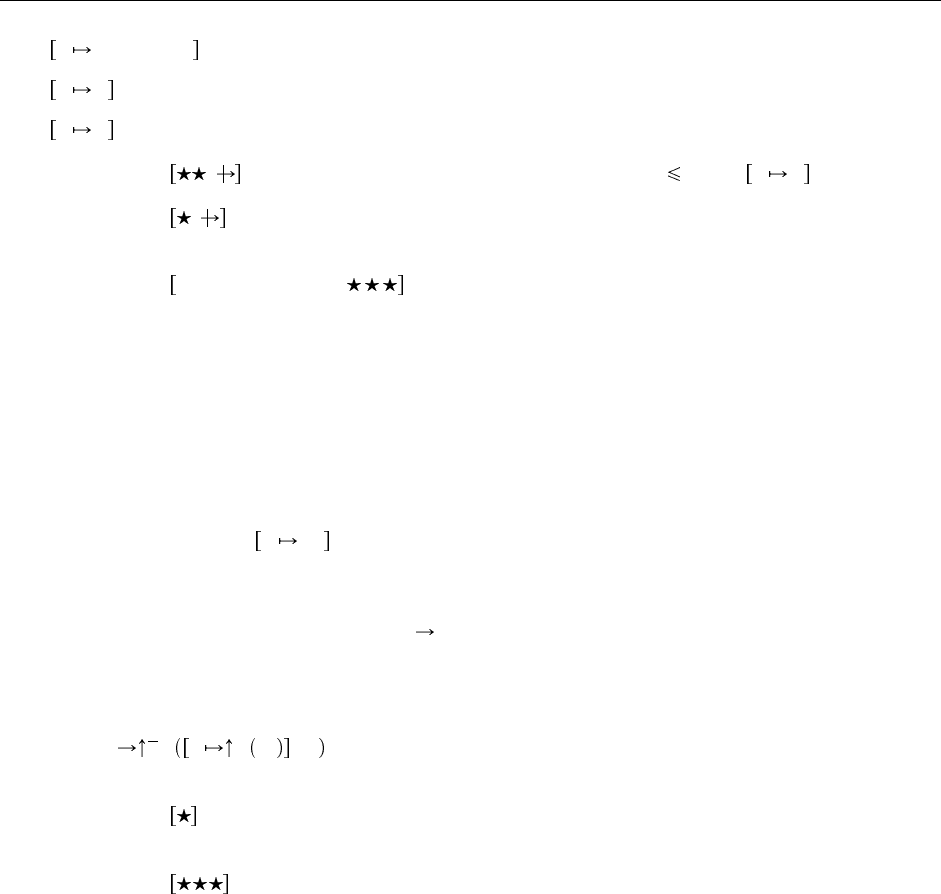
6.3. Вычисление 69

2. b a (λz. a) (b (λx.b))

3. b a (λb. b a)

4. b a (λa. b a)

Упражнение 6.2.6 , : Покажите, что если s и t — n-термы, и j n, то j s t — n-терм.

Упражнение 6.2.7 , : Возьмите лист бумаги и, не глядя на определения подстановки и сдвига,

сочините их заново.

Упражнение 6.2.8 Рекомендуется, : Определение подстановки на безымянных термах долж-

но быть согласовано с нашим неформальным определением подстановки на обыкновенных термах. (1)

Какую теорему нужно доказать, чтобы строго обосновать это утверждение? (2) Докажите ее.

6.3. Вычисление

Единственное, что нам требуется сделать, чтобы определить отношение вычисления на безымянных

термах — изменить правило бета-редукции, чтобы оно использовало нашу новую операцию подстановки

(это единственное правило в старой системе, которое упоминает имена переменных).

Нетривиальная деталь состоит в том, что редукция редекса «съедает» связанную переменную: при

редукции из ((λx.t

в x v

связанная переменная x исчезает. Таким образом, переменные

в результате подстановки надо перенумеровать, чтобы отразить тот факт, что x больше не является

частью контекста. Например:

(λ. 1 0 2) (λ. 0) 0 (λ.0) 1 (а не 1 (λ.0) 2)

Точно так же, требуется сдвинуть переменные в v

перед подстановкой в t

, поскольку терм t

определен в более крупном контексте, чем v

. Собирая все эти соображения вместе, получаем правило

бета-редукции такого вида:

(λ.t

) v

(E-AppAbs)

Остальные правила остаются такими же, как и раньше (Рис. 5.3).

Упражнение 6.3.1 : Нужно ли нам волноваться, что отрицательный сдвиг в правиле создаст

неправомерные термы с отрицательными индексами переменных?

Упражнение 6.3.2 : В исходной статье де Брауна содержалось два способа добиться безымянно-

го представления термов: индексы де Брауна, которые нумеруют связывающие выражения «изнутри

наружу», и уровни де Брауна, которые нумеруют связывающие выражения «снаружи внутрь». На-

пример, терм λx. (λy. x y) x представляется индексами де Брауна в виде λ. (λ. 1 0) 0, а уровня-

ми де Брауна в виде λ. (λ. 0 1) 0. Определите этот вариант с должной строгостью, и покажите,

что представления термов с использованием индексов и уровней изоморфны (т. е., каждое из них

можно однозначно восстановить, исходя из другого).

rev. 104

70 6.3. Вычисление

rev. 104