Пирс Б. Типы в языках программирования

Подождите немного. Документ загружается.

8.3. Безопасность = продвижение + сохранение 81

что t

. Если t

— значение, то, как следует из леммы о канонических формах, t

равняется

либо true, либо false, а следовательно, к t можно применить либо E-IfTrue, либо E-IfFalse. С

другой стороны, если t

, то, по правилу E-If, t if t

then t

else t

Вариант T-Succ: t succ t

: Nat

Согласно предположению индукции, либо t

является значением, либо существует какой-то t

, та-

кой, что t

. Если t

является значением, то, по лемме о канонических формах, это должно

быть числовое значение, а тогда t — тоже значение. С другой стороны, если t

, то, по правилу

E-Succ, succ t

succ t

Вариант T-Pred: t pred t

: Nat

Согласно предположению индукции, либо t

является значением, либо существует какой-то t

, та-

кой, что t

. Если t

является значением, то, по лемме о канонических формах, это должно

быть числовое значение, либо 0, либо succ nv

для некоторого nv

, и тогда к t применимо одно из

правил E-PredZero или E-PredSucc. Если, с другой стороны, t

, то, по правилу E-Pred,

pred t

Вариант T-IsZero: t iszero t

: Nat

Доказывается аналогичным образом.

Доказательство, что типы сохраняются при вычислении, в этой системе также не представляет

труда.

Теорема 8.3.3 Сохранение : Если t : T и t t , то t : T.

Доказательство: Индукция по дереву вывода t : T. На каждом шаге индукции мы предполагаем, что

требуемое свойство выполняется для всех поддеревьев (т. е., если s : S и s s , то s : S, когда s

: S доказано в поддереве текущего вывода), и рассматриваем варианты последнего правила в выводе

типа (мы демонстрируем лишь некоторые варианты; остальные устроены аналогично).

Вариант T-True: t true T Bool

Если последнее правило вывода T-True, то из формы этого правила нам известно, что t — кон-

станта true, а T — тип Bool. Но в таком случае, t является значением, невозможно, чтобы для

какого-либо t имелось t t , и требования теоремы просто не могут нарушаться.

Вариант T-If: t if t

then t

else t

: Bool t

: T t

: T

Если последнее правило в выводе типа было T-If, то из формы этого правила нам известно, что t

имеет вид if t

then t

else t

, для некоторых t

, t

и t

. Кроме того, должны существовать

деревья вывода с заключениями t

: Bool, t

: T и t

: T. При взгляде на правила вычисления, где

левая сторона представляет собой условное выражение, мы видим три правила, которые могут при-

вести к заключению t t : E-IfTrue, E-IfFalse и E-If. Рассмотрим их по отдельности (за выче-

том E-IfFalse, которое аналогично E-IfTrue):

Подвариант E-IfTrue: t

true t t

Если t t выводится по правилу E-IfTrue, то из формы этого правила мы видим, что

должен равняться true, а результат t должен равняться подвыражению t

. Следова-

тельно, требуемое утверждение доказано, так как нам известно (из предположений для

варианта T-If), что t

: T, чего нам и надо.

Подвариант E-If: t

t if t

then t

else t

Из предположений для варианта T-If нам известно, что в исходном дереве вывода есть

поддерево с заключением t

: Bool. К этому поддереву мы можем применить предпо-

ложение индукции и получить t

: Bool. В сочетании с известными нам (из предполо-

жений для варианта T-If) утверждениями, что t

: T и t

: T, это дает нам право

применить правило T-If и заключить, что if t

then t

else t

: T, или, что то же

самое, t : T.

Вариант T-Zero: t 0 T Nat

Невозможно (по тем же причинам, что и T-True).

Вариант T-Succ: t succ t

T Nat t

: Nat

Рассматривая правила вычисления на Рис. 3.2, мы видим, что есть только одно правило, E-Succ,

годное для вывода t t . Из формы этого правила ясно, что t

. Поскольку мы знаем, что

rev. 104

82 8.3. Безопасность = продвижение + сохранение

: Nat, мы можем по предположению индукции заключить, что t

: Nat, а отсюда, по правилу

T-Succ, succ t

: Nat, т. е., t : Nat.

Упражнение 8.3.4 : Перестройте доказательство так, чтобы индукция велась не по деревьям

вывода типизации, а по деревьям вывода для отношения вычисления.

Теорема о сохранении часто называется теоремой о редукции субъекта (или вычислении субъекта).

Интуиция здесь такова, что утверждение о типизации t : T можно представлять как предложение

«t имеет тип T». Терм t является подлежащим (субъектом) этого предложения, и свойство редукции

субъекта говорит в таком случае, что истинность предложения сохраняется при редукции субъекта.

В отличие от единственности типов, которая присутствует в одних системах и отсутствует в других,

продвижение и сохранение останутся важнейшими требованиями для всех систем типов, которые нам

предстоит рассмотреть.

Упражнение 8.3.5 : Правило вычисления E-PredZero (Рис. 3.2) не совсем согласуется с интуи-

цией: кажется, что было бы естественней считать, что предшественник нуля не определен, а не

определять его как ноль. Можно ли исправить это, просто убрав правило E-PredZero из определе-

ния одношагового вычисления?

Упражнение 8.3.6 Рекомендуется, : Поскольку есть свойство редукции субъекта, можно заду-

маться, насколько выполняется обратное свойство — расширение субъекта. Всегда ли, если t t

и t : T, верно, что t : T? Если да, докажите; если нет, приведите контрпример.

Упражнение 8.3.7 Рекомендуется, : Допустим, наше отношение вычисления определено в сти-

ле с большим шагом, как в Упраженении 3.5.17. Как в таком случае нужно формализовать интуи-

тивное свойство типовой безопасности?

Упражнение 8.3.8 Рекомендуется, : Допустим, наше отношение вычисления расширено так,

чтобы бессмысленные термы сводились к явному состоянию wrong, как в Упраженении 3.5.16. Как

теперь определить типовую безопасность?

Дорога от бестипового мира к

типизированному была

пройдена многократно, в

различных областях знания, и

во многом по одним и тем же

причинам.

Лука Карделли и Питер Вегнер

(Cardelli and Wegner 1985)

Существуют языки, где эти свойства не выполняются, притом, что языки все же можно считать безопасными с точки

зрения типов. Например, при формализации операционной семантики Java в стиле с малым шагом (Flatt, Krishnamurthi

and Felleisen 1998a; Igarashi, Pierce and Wadler 1999) сохранение типов в данной нами здесь форме отсутствует (подробно-

сти см. в Главе 19). Однако это следует рассматривать как недостаток конкретного подхода к формализации, а не самого

языка, поскольку он исчезает, например, при переходе к семантике с большим шагом.

rev. 104

Глава 9

Простое типизированное

лямбда-исчисление

В этой главе вводится самое простое из семейства типизированных исчислений, которые мы будем

изучать в оставшейся части книги: простое типизированное лямбда-исчисление Чёрча (Church 1940) и

Карри (Curry 1958).

9.1. Типы функций

В Главе 8 мы определили простую статическую систему типов для арифметических выражений с

двумя типами: Bool, относящимся к термам, чье вычисление дает булевское значение, и Nat, отно-

сящимся к термам, при вычислении которых получается число. «Плохо типизированные» термы, не

попадающие ни в один из этих типов, включают как все термы, которые при вычисление попадают

в тупиковое состояние (напр., if 0 then 1 else 2), так и некоторые термы, которые на самом деле

при вычислении ведут себя как надо, но по отношению к которым наша статическая классификация

оказывается чересчур осторожной (скажем, if true then 0 else false).

Допустим, нам нужно построить подобную систему типов для языка, где булевские значения (для

краткости в этой главе мы забудем про числа) сочетаются с примитивами чистого лямбда-исчисления.

А именно, мы хотим ввести правила типизации для переменных, абстракций и применений, которые

(а) поддерживают типовую безопасность — т. е., удовлетворяют теоремам о продвижении (8.3.2) и

сохранении (8.3.3), — и при этом (б) не слишком консервативны, — т. е., они должны уметь присваивать

типы большинству программ, которые нам на самом деле хотелось бы написать.

Разумеется, поскольку чистое лямбда-исчисление полно по Тьюрингу, нет даже надежды дать точ-

ный типовый анализ для всех примитивов. Например, нет никакого надежного способа понять, возвра-

щает ли программа

if <долгое и сложное вычисление> then true else (λx.x)

булевское значение или функцию, не запустив сначала долгое и сложное вычисление и не посмотрев,

выдало ли оно истину или ложь. В общем случае, долгое и сложное вычисление может вообще не

завершиться, и тогда всякий вычислитель, который попытается предсказать его исход, тоже никогда

не выдаст результата.

Ясно, что, если мы хотим расширить систему типов с булевскими значениями и добавить к ней

функции, нам нужно ввести тип, относящийся к термам, чье вычисление дает в результате функцию.

В качестве первого приближения, давайте назовем этот тип . Если мы введем правило типизации

λx.t :

В этой главе изучается простое типизированное лямбда-исчисление (Рис. 9.1) с булевскими значениями (Рис. 8.1).

Реализация на OCaml называется fullsimple.

84 9.2. Отношение типизации

дающее всякой абстракции тип , то как простые термы, вроде λx.x, так и сложные, вроде if true

then (λx.true) else (λx.λy.y), будут отмечены как дающие функции при вычислении.

Однако такой простой анализ явно чересчур консервативен: например, функции λx.true и λx.λy.y

попадают в одну группу и получают один и тот же тип. При этом игнорируется, что применение одной

функции к аргументу дает булевское значение, а применение другой дает снова функцию. В общем

случае, чтобы сообщить осмысленный тип результату применения, нам нужно знать о его левой части

нечто большее, чем просто то, что это функция; нужно знать, что за тип эта функция возвращает.

Более того, чтобы быть уверенными, что функция поведет себя правильно при вызове, нужно следить,

какого типа аргументы она ожидает. Ради отслеживания этой информации мы заменяем простой тип

бесконечным семейством типов вида T

, каждый из которых описывает функции, принимающие

аргументы типа T

и возвращающие результаты типа T

Определение 9.1.1 Множество простых типов на основе типа Bool порождается следующей грам-

матикой:

T ::= типы:

Bool тип булевских значений

T T тип функций

Конструктор типов право-ассоциативен — то есть, выражение T

обозначает T

Например, Bool Bool — тип функций, переводящих булевские аргументы в булевские резуль-

таты. (Bool Bool) (Bool Bool), или, что то же самое, (Bool Bool) Bool Bool —

тип функций, принимающих функции, переводящие булевские значения в булевские значения, и воз-

вращающих такие же функции.

9.2. Отношение типизации

Чтобы присвоить тип абстракции вида λx.t, нужно понять, что случится, когда эта абстракция

будет применена к какому-либо аргументу. Немедленно возникает вопрос: откуда мы знаем, какого

типа аргументов следует ожидать? На этот вопрос возможны два ответа: либо мы просто помечаем λ-

абстракцию типом ожидаемого аргумента, либо анализируем ее тело, смотрим, как используется в нем

аргумент, и пытаемся определить, какого типа он должен быть. Сейчас мы выбираем первый вариант.

Вместо выражения λx.t мы будем писать λx:T

, так что аннотация при связанной переменной будет

нам говорить, что аргумент имеет тип T

Языки, где для помощи процедуре проверки типов используются аннотации на термах, называются

явно типизированными. Языки, где программа проверки типов пытается вывести или реконструиро-

вать эту информацию, называются неявно типизированными. (В литературе по λ-исчислению исполь-

зуется также термин системы присвоения типов.) По большей части в этой книге рассматриваются

явно типизированные языки; неявной типизации посвящена Глава 22.

Когда известен тип аргумента, ясно, что тип результата функции совпадает с типом тела t

, полу-

ченным исходя из предположения, что вхождения x внутри t

обозначают термы типа T

. Эта интуиция

выражается следующим правилом типизации:

x:T

λx:T

: T

(T-Abs)

Поскольку в термах может содержаться по несколько λ-абстракций, в общем случае нам придется гово-

рить о нескольких подобных предположениях. Таким образом, отношение типизации из двухместного,

t : T, становится трехместным, Γ t : T, где Γ — множество предположений о типах свободных

переменных в t.

Формально, контекст типизации (также называемый окружение типизации) Γ представляет со-

бой последовательность переменных и их типов, а операция «запятая» расширяет Γ, добавляя к нему

справа новое связывание. Пустой контекст иногда изображается символом , однако чаще всего мы

просто его опускаем, получая запись t : T «Замкнутый терм t имеет тип T, исходя из пустого

множества предположений».

Чтобы избежать конфликтов между новым связыванием и связываниями, уже присутствующими

в Γ, мы требуем, чтобы имя x отличалось от переменных, связанных в Γ. Поскольку у нас действует

rev. 104

9.2. Отношение типизации 85

соглашение, что переменные, связанные λ-абстракциями, разрешается переименовывать, это требова-

ние всегда можно выполнить, переименовав, если надо, связанную переменную. Таким образом, всегда

можно представлять Γ как конечную функцию, переводящую переменные в их типы. Согласно этой

интуиции, мы пишем dom Γ для обозначения множества переменных, присутствующих в Γ.

Правило для типизации абстракций в общем случае имеет вид

Γ, x:T

Γ λx:T

: T

(T-Abs)

то есть, предпосылка имеет на одно или более предположение больше, чем заключение правила.

Правило типизации для переменных также немедленно следует из этого обсуждения: тип перемен-

ной таков, как мы сейчас предполагаем.

x : T Γ

Γ x : T

(T-Var)

Предпосылка x:T Γ читается «Согласно Γ, предполагается, что x имеет тип T».

Наконец, нам нужно иметь правило типизации для применений.

Γ t

: T

Γ t

: T

Γ t

: T

(T-App)

Если t

дает при вычислении функцию, переводящую аргументы типа T

в результаты типа T

(исходя

из предположения, что значения, обозначаемые его свободными переменными, имеют типы, предписан-

ные им в Γ), и если t

дает при вычислении результат типа T

, то результат применения t

к аргументу

будет иметь тип T

Правила типизации для булевских констант и условных выражений остаются такими же, как прежде

(Рис. 8.1). Заметим, однако, что метапеременная T в правиле для условных выражений

: Bool t

: T t

: T

if t

then t

else t

: T

(T-If)

теперь может замещаться любыми функциональными типами. Это позволяет нам строить условные

выражения с результатами-функциями:

if true then (λx: Bool . x) else (λx : Bool . not x );

(λx : Bool . x) : Bool -> Bool

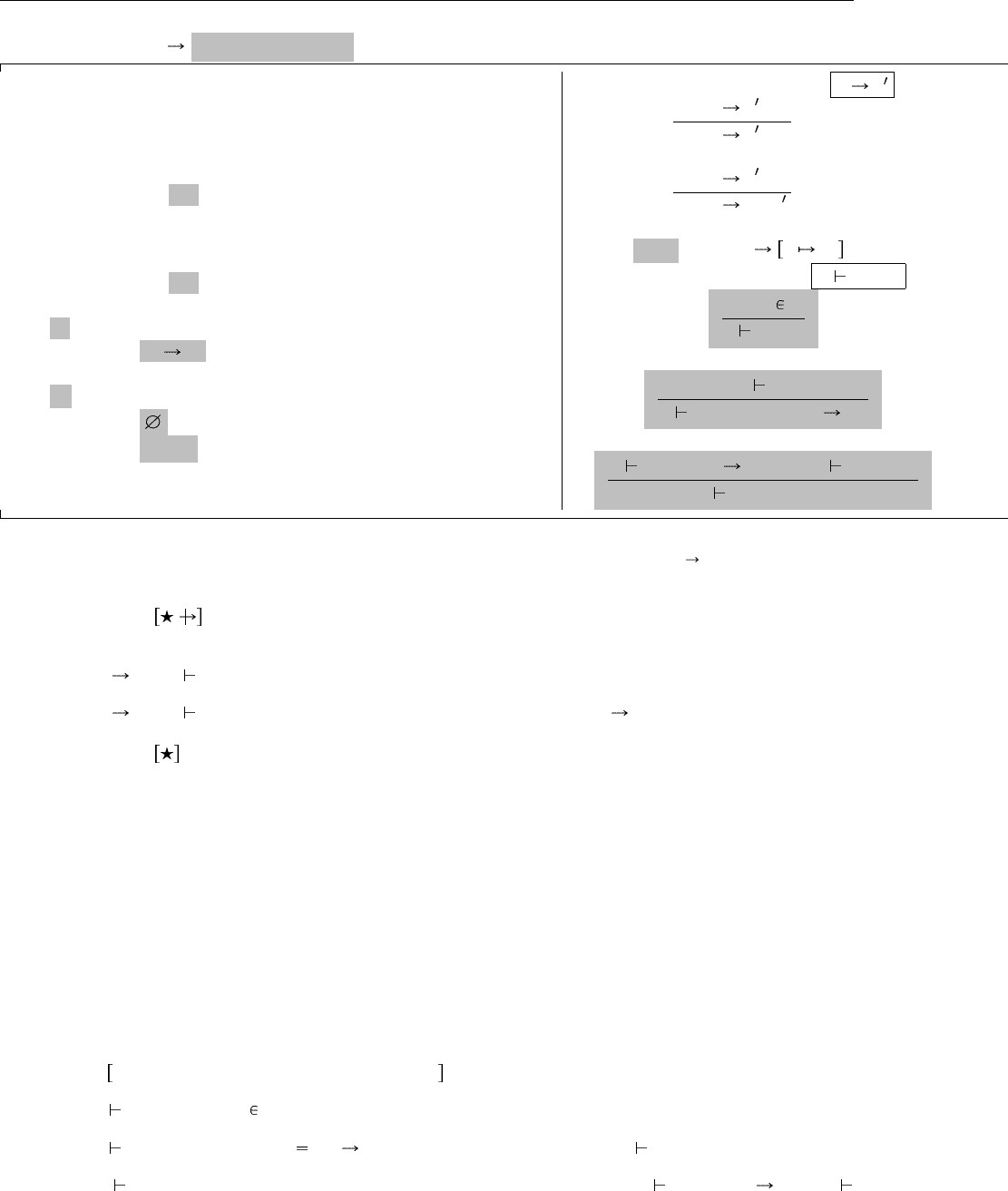
Все эти правила типизации сведены вместе на Рис. 9.1 (для полноты они дополнены описанием

синтаксиса и правил вычисления). Серым цветом на рисунке выделен материал, который отличает

новую систему от бестипового лямбда-исчисления — как новые правила, так и фрагменты, добавляемые

к старым. Как и в случае с булевскими значениями и числами, мы разбили определение исчисления на

две части: чистое простое типизированное лямбда-исчисление, где вообще нет никаких базовых типов

(оно изображено на этом рисунке), и отдельный набор правил для булевских значений, который мы

уже видели на Рис. 8.1 (разумеется, к каждому правилу типизации на этом рисунке нужно добавить

контекст Γ).

Часто для обозначения простого типизированного лямбда-исчисления мы будем использовать сим-

вол λ (им же мы будем обозначать системы с другим набором базовых типов).

Упражнение 9.2.1 : На самом деле, чистое простое типизированное лямбда-исчисление без базовых

типов является вырожденным, поскольку в нем нет ни одного правильно типизированного терма.

Почему?

Из экземпляров правил типизации для λ можно конструировать деревья типизации, как мы уже

делали для арифметических выражений. Например, вот вывод, показывающий, что терм (λx:Bool.x)

true имеет тип Bool в пустом контексте.

x:Bool x:Bool

T-Var

λx:Bool.x : Bool Bool

T-Abs

true : Bool

T-True

(λx:Bool.x) true : Bool

T-App

Начиная с этого момента, примеры простого взаимодействия с интерпретаторами обычно будут показывать не только

результаты, но и их типы (мы будем их иногда пропускать, если они очевидны).

rev. 104

86 9.3. Свойства типизации

(типизированное) Основано на λ(5.3)

Синтаксис

t ::= термы:

x переменная

λ x :T .t абстракция

t t применение

v ::= значения:

λ x :T .t значение-абстракция

T ::= типы:

T T тип функций

Γ ::= контексты:

пустой контекст

Γ, x:T связывание термовой переменной

Вычисление t t

(E-App1)

(E-App2)

(λ x :T

) v

x v

(E-AppAbs)

Типизация Γ t : T

x : T Γ

Γ x : T

(T-Var)

Γ, x:T

: T

Γ λx:T

: T

(T-Abs)

Γ t

: T

Γ t

: T

Γ t

: T

(T-App)

Рис. 9.1. Чистое простое типизированное лямбда-исчисление (λ )

Упражнение 9.2.2 : Покажите (построив деревья вывода), что следующие термы имеют заяв-

ленные типы:

1. f:Bool Bool f (if false then true else false) : Bool

2. f:Bool Bool λx:Bool. f (if x then false else x) : Bool Bool

Упражнение 9.2.3 : Найдите контекст Γ, в котором терм f x y имеет тип Bool. Можете ли

вы кратко охарактеризовать множество всех таких контекстов?

9.3. Свойства типизации

Как и в Главе 8, прежде, чем доказывать типовую безопасность, нам нужно установить несколько

простых лемм. Большинство из них подобны тем, что мы уже видели ранее — нужно просто доба-

вить к отношению типизации контексты и в каждое доказательство ввести пункты, относящиеся к

λ-абстракциям, применениям и переменным. Единственное утверждение, которое действительно ново

— это лемма о подстановке (9.3.8).

Прежде всего, лемма об обращении содержит набор наблюдений о том, как строятся деревья вывода

типов: пункт, относящийся к каждой синтаксической форме терма, говорит «если терм данной формы

правильно типизирован, то его подтермы должны иметь такие-то типы. . . ».

Лемма 9.3.1 Обращение отношения типизации :

1. Если Γ x : R, то x:R Γ.

2. Если Γ λx:T

: R, то R T

для некоторого R

, и Γ, x:T

: R

3. Если Γ t

: R, то имеется некоторый тип T

, такой, что Γ t

: T

R и Γ

: T

rev. 104

9.3. Свойства типизации 87

4. Если Γ true : R, то R Bool.

5. Если Γ false : R, то R Bool.

6. Если Γ if t

then t

else t

: R, то Γ t

: Bool и Γ t

, t

: R.

Доказательство: Лемма непосредственно следует из определения отношения типизации.

Упражнение 9.3.2 Рекомендуется, : Существуют ли такие контекст Γ и тип T, что Γ

x x : T? Если да, то приведите пример Γ и T, и постройте дерево вывода Γ x x : T; если нет, то

докажите это.

В §9.2 мы выбрали для нашего исчисления представление с явной типизацией, чтобы облегчить за-

дачу проверки типов. При этом нам пришлось добавить аннотации типов — но только в определениях

связанных переменных и больше нигде. В каком смысле этого «достаточно»? Один из ответов на этот

вопрос дает теорема о единственности типов, которая сообщает нам, что правильно типизированные

типы находятся в однозначном соответствии со своими деревьями вывода типов: по терму можно одно-

значно восстановить дерево его вывода (и, разумеется, наоборот). В сущности, соответствие настолько

близкое, что нет почти никакой разницы между термом и его деревом вывода.

Теорема 9.3.3 Единственность типов : В любом заданном контексте типизации Γ терм t (где

все свободные переменные лежат в области определения Γ) имеет не более одного типа. То есть, если

терм типизируем, то тип у него только один. Более того, существует только одно дерево вывода

на основе правил, порождающих отношение типизации.

Доказательство: Упражнение. Доказательство, в сущности, настолько прямолинейно, что почти

не о чем говорить; однако выписывание всех деталей служит хорошей тренировкой по «выстраива-

нию» доказательств, касающихся отношения типизации.

Во многих системах типов, с которыми мы встретимся позднее в книге, такое простое соответствие

между термами и деревьями вывода отсутствует: один и тот же терм может обладать несколькими

типами, и каждый из них можно обосновать несколькими деревьями вывода. В этих системах часто

будет требоваться нетривиальная работа, чтобы показать, что из термов можно эффективно получить

деревья вывода типов.

Следующая лемма, о канонических формах, показывает, какой вид могут иметь значения различных

типов.

Лемма 9.3.4 Канонические формы :

1. Если v — значение типа Bool, то v равно либо true, либо false.

2. Если v — значение типа T

, то v = λx:T

Доказательство: Не представляет сложности. (Подобно доказательству леммы о канонических фор-

мах для арифметических выражений, 8.3.1.)

С помощью леммы о канонических формах мы можем доказать теорему о продвижении, подобную

Теореме 8.3.2. Утверждение теоремы нуждается в небольшой поправке: нас интересуют только за-

мкнутые термы, без свободных переменных. Для незамкнутых термов теорема неверна: терм f true

является нормальной формой, но не значением. Однако отсутствие такой теоремы не означает, что

язык чем-то плох, поскольку полные программы — термы, вычисление которых нас на самом деле

интересует, — всегда замкнуты.

Теорема 9.3.5 Продвижение : Допустим, t — замкнутый, правильно типизированный терм (т. е.,

для некоторого типа T, t : T). Тогда либо t является значением, либо имеется терм t , такой,

что t t .

Доказательство: Прямолинейная индукция по деревьям вывода типов. Варианты с булевскими кон-

стантами и условными выражениями точно повторяют доказательство теоремы о продвижении

rev. 104

88 9.3. Свойства типизации

для типизированных арифметических выражений (8.3.2). Вариант с переменной не может возник-

нуть (поскольку t замкнут). Вариант с абстракцией следует непосредственно, поскольку абстракции

— значения.

Единственный интересный вариант — применение, где t t

, причем t

: T

. По предположению индукции, либо t

является значением, либо он может произвести

шаг вычисления, и то же самое верно для t

. Если t

может сделать шаг, то к t применимо правило

E-App1. Если t

— значение, а t

может сделать шаг, то к t применимо E-App2. Наконец, если t

и t

оба значения, то лемма о канонических формах говорит нам, что t

имеет вид λx:T

, так

что к t применимо правило E-AppAbs.

Нашей следующей задачей будет доказать, что вычисление сохраняет типы. Для начала мы сформу-

лируем парочку «структурных лемм» об отношении типизации. Сами по себе они не особенно интерес-

ны, но в последующих доказательствах они помогут нам проводить некоторые полезные преобразования

с деревьями вывода типов.

Первая структурная лемма утверждает, что мы можем переставлять элементы контекста, как нам

удобно, не изменяя при этом множество утверждений о типах, выводимых из этого контекста. Напом-

ним (стр. 84), что все связывания в контексте должны иметь различные имена, и что каждый раз,

добавляя к контексту новое связывание, мы молчаливо предполагаем, что новое имя отличается от

уже присутствующих в контексте (в случае необходимости мы можем применить Соглашение 5.3.4 и

переименовать новую переменную).

Лемма 9.3.6 Перестановка : Если Γ t : T, и ∆ представляет собой перестановку Γ, то ∆

t : T. Более того, глубина дерева вывода остается неизменной.

Доказательство: Несложная индукция по деревьям вывода типов.

Лемма 9.3.7 Ослабление : Если Γ t : T, и x dom Γ , то Γ, x:S t : T. Более того, глубина

дерева вывода остается неизменной.

Доказательство: Несложная индукция по деревьям вывода типов.

При помощи этих вспомогательных лемм мы можем доказать ключевое свойство отношения ти-

пизации: правильная типизированность сохраняется, когда вместо переменных подставляются термы

соответствующих типов. Подобные леммы играют настолько большую роль в доказательствах коррект-

ности языков программирования, что часто их просто называют «леммами о подстановке».

Лемма 9.3.8 Сохранение типов при подстановке : Если Γ, x:S t : T и Γ s : S, то Γ x

s t : T.

Доказательство: Индукция по глубине вывода утверждения Γ, x:S t : T. Для каждого данного

вывода мы рассматриваем варианты последнего использованного правила типизации.

Наиболее ин-

тересные варианты — переменная и абстракция.

Вариант T-Var: t = z

где z:T Γ, x:S

Требуется рассмотреть два подварианта, в зависимости от того, совпадает ли z с x или это разные

переменные. Если z = x, то x s z s. Требуемый результат тогда Γ s : S, а это одна из

предпосылок леммы. В противном случае, x s z z, и результат следует непосредственно.

Вариант T-Abs: t = λy:T

T = T

Γ, x:S, y:T

: T

По соглашению 5.3.4, мы можем считать, что x y и y F V s . Согласно лемме о перестановке для

одного из поддеревьев, получаем Γ, y:T

, x:S t

: T

. По лемме об ослаблении для другого поддерева

(Γ s : S) получаем Γ, y:T

s : S. Согласно предположению индукции, получается Γ, y:T

x s t

: T

. По правилу T-Abs, Γ λy:T

. x s t

: T

. Но это именно то утверждение,

которое нам нужно, поскольку, по определению подстановки, x s t λy:T

. x s t

Или, что равносильно, варианты возможной формы t, поскольку для каждого синтаксического конструктора у нас

ровно одно правило типизации.

rev. 104

9.4. Соответствие Карри-Ховарда 89

Вариант T-App: t = t

Γ, x:S t

: T

Γ, x:S t

: T

T = T

Согласно предположению индукции, Γ x s t

: T

и Γ x s t

: T

. По правилу

T-App, Γ x s t

x s t

: T, т. е., Γ x s t : T.

Вариант T-True: t = true

T = Bool

В этом случае x s t true, и требуемый результат Γ x s t : T следует непосредственно.

Вариант T-False: t = false

T = Bool

Аналогично.

Вариант T-If: t = if t

then t

else t

Γ, x:S t

: Bool

Γ, x:S t

: T

Γ, x:S t

: T

Три раза применяя предположение индукции, имеем

Γ x s t

: Bool

Γ x s t

: T

Γ x s t

: T,

и утверждение леммы следует по правилу T-If.

Используя лемму о подстановке, мы можем доказать вторую половину теоремы о типовой безопас-

ности — то, что вычисление сохраняет типизацию.

Теорема 9.3.9 Сохранение : Если Γ t : T и t t , то Γ t : T.

Доказательство: Упражнение Рекомендуется, . Структура доказатетельства очень

похожа на доказательство теоремы о сохранении для арифметических выражений (8.3.3), за исклю-

чением обращения к лемме о подстановке.

Упражнение 9.3.10 Рекомендуется, : В Упражнении 8.3.6 мы исследовали свойство расшире-

ния субъекта для простого исчисления, работающего с арифметическими выражениями. Выполня-

ется ли это свойство для «функциональной части» протого типизированного лямбда-исчисления?

А именно, допустим, что t не содержит условных выражений. Можно ли, исходя из t t и

Γ t : T, сделать вывод Γ t : T?

9.4. Соответствие Карри-Ховарда

Конструктору вроде « » соответствуют два вида правил:

1. Правило введения (T-Abs), показывающее, как элементы типа могут создаваться, и

2. правило удаления (T-App), показывающее, как элементы типа могут использоваться.

В случае, когда форма, вводящая элемент типа (λ) служит непосредственным подтермом формы, ис-

пользующей его (применение), получается редекс — место, где может произойти вычисление.

Рассуждения о правилах введения и удаления часто оказываются полезными при исследовании

систем типов. Позднее, когда мы доберемся до более сложных систем, при каждом конструкторе типов

будут иметься правила введения и удаления, связанные между собой.

Упражнение 9.4.1 : Какие из правил для типа Bool на Рис. 8.1 являются правилами введения, а

какие правилами удаления? Что можно сказать о правилах для типа Nat на Рис. 8.2?

Терминология «правила введения/удаления» происходит из соответствия между теорией типов и

логикой, известного как соответствие Карри-Ховарда или изоморфизм Карри-Ховарда (Curry and

Feys 1958; Howard 1980). Вкратце, идея состоит в том, что в конструктивных логиках доказательство

rev. 104

90 9.5. Стирание типов и типизируемость

утверждения P состоит в демонстрации конкретного свидетельства в пользу P .

Карри и Ховард

заметили, что это свидетельство во многом похоже на вычисление. Например, доказательство утвер-

ждения P Q можно рассматривать как механическую процедуру, которая, получая доказательство

P , строит доказательство Q, — или, с другой точки зрения, доказательство Q, абстрагированное от

доказательства P . Подобным образом, доказательство P Q состоит из доказательства P в сочетании

с доказательством Q. Такое наблюдение ведет к следующему соответствию:

Логика Языки программирования

утверждения типы

утверждение P Q тип P Q

утверждение P Q тип P Q (см. §11.6)

доказательство утверждения P терм t типа P

утверждение P доказуемо тип P населен (т. е., существуют термы типа P)

С этой точки зрения, терм в простом типизированном лямбда-исчислении является доказательством

логического утверждения, соответствующего его типу. Вычисление — редукция на лямбда-термах, —

соответствует логической операции упрощения доказательств методом устранения сечений. Соответ-

ствие Карри-Ховарда называют также аналогией «утверждения как типы». Его подробные обсужде-

ния можно найти во многих источниках, в том числе в книге Жирара, Лафонта и Тейлора (Girard,

Lafont and Taylor 1989), у Галье (Gallier 1993), Сёренсена и Ужичина (Sørensen and Urzyczyn 1998),

Пфеннинга (Pfenning 2001), Губо-Ларрека и Макки (Goubault-Larrecq and Mackie 1997), а также у

Симмонса (Simmons 2000).

Красота соответствия Карри-Ховарда в том, что оно не ограничено какой-то одной системой типов

и одной логикой — напротив, его можно распространить на широкий спектр систем типов и логик. На-

пример, Система F (Глава 23), где параметрический полиморфизм связан с квантификацией по типам,

в точности соответствует конструктивной логике второго порядка, где разрешена квантификация по

утверждениям. Система F

(Глава 30) соответствует логике высших порядков. Более того, часто это

соответствие использовалось, чтобы переносить результаты из одной области в другую. Так, линейная

логика Жирара (Girard 1987) приводит к идее систем линейных типов (Wadler 1990; Wadler 1991;

Turner, Wadler and Mossin 1995; Hodas 1992; Mackie 1994; Chirimar, Gunter and Riecke 1996; Kobayashi,

Pierce and Turner 1996, и многие другие), в то время как модальные логики использовались при разра-

ботке систем частичного вычисления и порождения кода во время выполнения (см. Davies and Pfenning

1996; Wickline, Lee, Pfenning and Davies 1998, и другие источники, цитируемые в указанных трудах).

9.5. Стирание типов и типизируемость

На Рис. 9.1 мы определили отношение вычисления прямо на просто типизированных термах.

Несмотря на то, что аннотации типов не играют при вычислении никакой роли — во время выпол-

нения мы не проводим никаких проверок, чтобы убедиться, что функции применяются к аргументам

подходящих типов, — мы таскаем эти аннотации за собой внутри вычисляемых термов.

Большинство компиляторов промышленных языков программирования избегают сохранять анно-

тации во время выполнения: они используются при проверке типов (и, в более сложно устроенных

компиляторах, во время порождения кода), однако в скомпилированной форме программы их нет. В

сущности, перед выполнением программы преобразуются обратно в бестиповую форму. Такой стиль се-

мантики можно формализовать при помощи функции стирания, переводящей типизированные термы

в соответствующие бестиповые термы.

Определение 9.5.1 Функция стирания просто типизированного терма t определяется так:

erase x x

erase λx:T

λx. erase t

erase t

Характерное различие между классическими и конструктивными логиками состоит в том, что в последних отстут-

ствует правило исключенного третьего, говорящее, что для всякого утверждения Q истинно либо само Q, либо Q.

Чтобы доказать Q Q в конструктивной логике, требуется предоставить свидетельство либо в пользу Q, либо в пользу

rev. 104