Пирс Б. Типы в языках программирования

Подождите немного. Документ загружается.

11.10. Варианты 111

<> Расширяет λ (9.1)

Новые синтаксические формы

t ::= . . . термы:

<l=t> as T постановка тега

case t of <l

>=>t

i 1..n

> case

v ::= . . . значения:

<l=v> as T значение с тегом

T ::= . . . типы:

i 1..n

> тип вариантов

Новые правила вычисления t t

case (<l

> as T) of <l

>=>t

i 1..n

(E-CaseVariant)

case t

of <l

>=>t

i 1..n

case t’

of <l

>=>t

i 1..n

(E-Case)

> as T <l

> as T

(E-Variant)

Новые правила типизации Γ t : T

Γ t

: T

Γ <l

> as <l

i 1..n

> : <l

i 1..n

(T-Variant)

Γ t

: <l

i 1..n

> для каждого i, Γ, x

Γ case t

of <l

> => t

i 1..n

: T

(T-Case)

Рис. 11.11. Варианты

extendT a b l e =

λt : Table . λm : Nat . λv: Nat .

λn : Nat :

if equal n m then < some =v > as OptionalNat

else t n;

extendT a b l e : Table -> Nat -> Nat -> Table

берет таблицу и добавляет в нее (или изменяет имеющуюся) ячейку, отображающую вход m в выход

<some=v>. (Функция equal определена в решении Упражнения 11.11.1 на стр. 393.)

Результат, полученный из поиска в таблице типа Table, можно использовать в выражении case.

Например, если у нас есть таблица t, и мы хотим получить значение, соответствующее числу 5, мы

можем написать

x = case t (5) of

< none =u > = > 999

| < some =v > = > v ;

выдавая 999 в качестве умолчательного значения x на случай, если t не определена в точке 5.

Во многих языках имеется встроенная поддержка опций. Например, в OCaml есть предопределен-

ный конструктор типов option, и многие функции в типичных программах на OCaml возвращают

опции. Значение null в языках вроде C, C++ и Java в сущности, представляет собой замаскированную

опцию. В этих языках переменная типа T (в случае, если T — «ссылочный тип», то есть, его значения

выделяются в куче) может содержать либо особое значение null, либо указатель на значение типа

T. То есть тип такой переменной на самом деле Ref(Option(T)), где Option(T)=<none:Unit,some:T>.

Конструкция Ref подробно обсуждается в Главе 13.

11.10.2. Перечисления

Два «вырожденных случая» типов-вариантов достаточно полезны, чтобы упомянуть их отдельно:

типы перечислений и варианты с одним полем.

Тип-перечисление — это вариантный тип, где с каждым полем ассоциирован тип Unit. Например,

тип, представляющий дни рабочей недели, можно определить так:

ДеньНедели

= понедельник <: Unit , вторник: Unit , среда: Unit ,четверг

: Unit , пятница: Unit >;

rev. 104

112 11.10. Варианты

Элементами этого типа являются термы вроде <понедельник:Unit> as ДеньНедели. Действительно,

поскольку в типе Unit всего один элемент, тип ДеньНедели имеет ровно пять значений, однозначно

соответствующих дням недели. При помощи конструкции case можно определять вычисления с ис-

пользованием перечислений.

следующийРабочийДень

= $\ L$wДеньНедели:.

case w of понедельник<=x > = > вторник<= unit > as ДеньНедели

| вторник <=x > = > среда<= unit > as ДеньНедели

| среда <=x > => четверг <= unit > as ДеньНедели

| четверг <=x > = > пятница<= unit > as ДеньНедели

| пятница <=x > = > понедельник<= unit > as ДеньНедели;

Разумеется, используемый нами конкретный синтаксис плохо приспособлен к написанию и чтению

таких программ. Некоторые языки (начиная с Паскаля) обладают особым синтаксисом для объявления

перечислений и работы с ними. Другие — например, ML, см. стр. 114, — представляют перечисления

как частный случай вариантных типов.

11.10.3. Варианты с одним полем

Еще один интересный частный случай представляют собой вариантные типы с единственной меткой

V = <l:T >;

На первый взгляд, такой тип не кажется особенно полезным: в конце концов, все элементы V находятся

во взаимно однозначном соответствии с элементами типа поля T, поскольку всякий элемент V имеет в

точности форму <l=t> для некоторого t : T. Существенно, однако, что стандартные операции над T

неприменимы к элементам V без распаковки: невозможно случайно перепутать V и T.

Предположим, например, что мы пишем программу для денежных расчетов в различных валютах.

В такой программе могут встретиться функции для перевода долларов в евро. Если и те, и другие

представлены как Float, эти функции могут выглядеть так:

долларыВевро

= λd: Float . timesf l o a t d 1.13 25;

долларыВевро : Float -> FloatевроВдоллары

= λe: Float . timesf l o a t e 0.8 83;

евроВдоллары : Float -> Float

(где функция timesfloat: Float->Float->Float служит для перемножения чисел с плавающей точ-

кой). Если мы начнем с долларовой суммы

мойБанковскийСчет

= 39.50;

то ее можно перевести в евро и затем обратно в доллары так:

евроВдолларыдолларыВевро

( мойБанковскийСчет)

39.4999 0 1 2 5 : Float

Все это вполне разумно выглядит. Но с такой же легкостью мы можем производить совершенно бес-

смысленные действия. Например, можно перевести сумму на счете в евро дважды:

долларыВевродолларыВевро

( мойБанковскийСчет);

50.660971875 : Float

Поскольку наши денежные суммы представлены просто как числа, система типов не может предотвра-

тить бессмыслицу такого рода. Однако, если мы определим доллары и евро как различные вариантные

типы (взяв числа с плавающей точкой в качестве внутреннего представления)

rev. 104

11.10. Варианты 113

СуммаВДолларах

= доллары <: Float >;СуммаВЕвро

= евро <: Float >;

мы сможем определить безопасные версии функций преобразования валют, в которых на вход непре-

менно должна подаваться сумма в правильной валюте:

долларыВевро

λdСуммаВДолларах:.

case d of доллары<=x > = >евро

< = timesfloat x 1.1325 > as СуммаВЕвро;

долларыВевро : СуммаВДолларах -> СуммаВЕвроевроВдоллары

λeСуммаВЕвро:.

case e of евро<=x > = >доллары

< = timesfloat x 0.883 > as СуммаВДолларах;

евроВдоллары : СуммаВЕвро -> СуммаВДолларах

Теперь процедура проверки типов способна следить, какие валюты используются у нас в вычислениях

и напоминать, как следует интерпретировать окончательный результат:

мойБанковскийСчет

= доллары <=39.50 > as СуммаВДолларах;евроВдолларыдолларыВевро

( мойБанковскийСчет);

доллары <=39.49990125 > as СуммаВДолларах : СуммаВДолларах

Более того, если мы напишем бессмысленное двойное преобразование, типы не сойдутся и программа

будет отвергнута (как и должно быть):

долларыВевродолларыВевро

( мойБанковскийСчет);

Ошибка : несоответствиетипапараметра

11.10.4. Варианты и типы данных

Вариантный тип <l

i 1..n

> приблизительно соответствует типу ML, который определяется так:

type T = l

of T

| l

of T

| ...

| l

of T

Однако стоит упомянуть несколько отличий.

1. Имеется несущественное, но, возможно, вносящее путаницу расхождение между нашими согла-

шениями по использованию больших букв и соглашениями, принятыми в OCaml. В OCaml имена

типов должны начинаться с маленькой буквы, а имена конструкторов (в нашей терминологии,

метки вариантов) — с большой, так что, строго говоря, объявление типа должно записываться

как

type t = L

of t

| ... | L

of t

Чтобы не смешивать термы t и типы T, мы будем в этом обсуждении игнорировать OCaml-овские

соглашения, и продолжать пользоваться собственными.

В этом разделе используется конкретный синтаксис типов данных OCaml, чтобы выдержать соответствие тем главам

книги, где обсуждается реализация интерпретаторов. Однако такие типы возникли в ранних диалектах ML, и их примерно

в такой же форме можно найти в Стандартном ML и в родственных языках вроде Haskell. Типы данных и сопоставление

с образцом — вероятно, самые большие преимущества этих языков в ежедневной работе.

rev. 104

114 11.10. Варианты

2. Наиболее интересное различие состоит в том, что OCaml не требует аннотации типа, когда

элемент типа T

с помощью конструктора l

переводится в тип T: можно просто писать l

(t).

OCaml добивается такой возможности (сохраняя при этом единственность типов) за счет требо-

вания, чтобы тип T объявлялся перед использованием. Более того, метки вариантов T не должны

использоваться никакими другими типами в той же области видимости. Таким образом, когда

процедура проверки типов встречает терм l

(t), она знает, что правильная аннотация может

быть только T. В сущности, аннотация «спрятана» внутрь метки варианта.

Такой трюк позволяет избавиться от множества глупых аннотаций, но вызывает и некоторое

недовольство пользователей, поскольку одну метку варианта нельзя использовать в нескольких

типах — по крайней мере, в рамках одного модуля. В Главе 15 мы рассмотрим другой способ

избежать аннотаций, лишенный этого недостатка.

3. Еще одна удобная хитрость OCaml заключается в том, что, когда тип данных, связанный с ва-

риантом, — просто Unit, его можно не указывать. В результате перечисления можно определять

так:

type Weekda y = monday | t uesday | w e dnesday | th ursday | friday

вместо такой записи:

type Weekda y = monday of Unit

| tuesday of Unit

| we d n esday of Unit

| th ursday of Unit

| friday of Unit

Кроме того, метка варианта monday сама по себе считается значением типа Weekday (а не метка

monday, примененная к вырожденному значению unit).

4. Наконец, типы данных OCaml увязывают вариантные типы с несколькими дополнительными

конструкциями, которые мы по отдельности будем исследовать в последующих главах.

• Определение типа данных может быть рекурсивным — т. е., имя определяемого типа может

встречаться в теле определения. Например, при стандартном определении списка натураль-

ных чисел значение с тегом cons — пара, второй элемент которой имеет тип NatList.

type NatLis t = nil

| cons of Nat * NatList

• Тип OCaml может быть параметризован типовой переменной, как, например, в общем опре-

делении типа списка List:

type ’a List = nil

| cons of ’a * ’a List

С точки зрения теории типов можно рассматривать List как особого рода функцию — назы-

ваемую типовым оператором, — переводящую каждый тип-аргумент ’a в конкретный тип

данных. . . Nat в NatList, и т. д. Типовые операторы обсуждаются в Главе 29.

11.10.5. Типы как неперекрывающиеся объединения

Типы-суммы и вариантные типы иногда называют неперекрывающимися объединениями. Тип T

— «объединение» T

и T

в том смысле, что элементы этого типа включают все элементы T

и T

. Это

объединение неперекрывающееся, поскольку множества элементов T

и T

перед собственно объедине-

нием помечены тегами, соответственно, inl и inr. Таким образом, всегда можно легко узнать, происхо-

дит ли определенный элемент из T

или из T

. Выражение тип-объединение, кроме того, применяется

к непомеченным (не-неперекрывающимся) типам объединений, описываемым в §15.7.

В тексте OCaml я использую англоязычные идентификаторы (в данном случае, названия дней недели). — прим.

перев.

rev. 104

11.11. Рекурсия общего вида 115

11.10.6. Динамика типов

Даже в языках со статической типизацией бывает необходимо иметь дело с данными, чей тип

невозможно определить на этапе компиляции. В частности, такое происходит, когда данные живут

на нескольких различных машинах или в течение нескольких запусков программы — например, когда

эти данные хранятся в базе данных или передаются по компьютерной сети. Чтобы безопасным образом

справляться с такими ситуациями, во многих языках присутствуют средства, позволяющие узнать тип

значений во время работы программы.

Один из привлекательных способов сделать это — добавить тип Dynamic, чьи значения представляют

собой пары из значения v и метки типа T, где v имеет тип T. Элементы типа Dynamic строятся при

помощи особой конструкции навешивания метки, а исследуются с помощью безопасной конструкции

typecase. В сущности, можно рассматривать Dynamic как бесконечного размера неперекрывающееся

объединение, где типы служат метками. См. работы Гордона (Gordon, ок. 1980), Майкрофта (Mycroft

1983), Абади, Карделли, Пирса и Плоткина (Abadi, Cardelli, Pierce and Plotkin 1983), Леруа и Мони

(Leroy and Mauny 1991), Абади, Карделли, Пирса и Реми (Abadi, Cardelli, Pierce and R´emy 1995), а

также Хенглейна (Henglein 1994).

11.11. Рекурсия общего вида

Еще одна возможность, доступная в большинстве языков программирования — определение ре-

курсивных функций. Мы уже видели (Глава 5, стр. 58), что в бестиповом лямбда-исчислении такие

функции можно определять при помощи комбинатора fix.

В типизированном языке рекурсивные функции можно определять подобным же образом. Напри-

мер, вот функция iseven, возвращающая true, будучи вызвана с четным аргументом, и false в про-

тивном случае:

λie :Nat - > Bool

λx : Nat .

if isze ro x then true

else if iszero ( pred x) then false

else ie ( pred ( pred x ));

ff : ( Nat -> Bool ) -> Nat -> Bool

is even = fix ff ;

is even : Nat -> Bool

is even 7;

false : Bool

Интуиция здесь такова: функция высшего порядка ff, передаваемая аргументом в fix, является гене-

ратором для функции iseven: если ff применяется к функции ie, чье поведение приближенно соот-

ветствует требуемому поведению iseven вплоть до некоторого числа n (то есть, к функции, возвраща-

ющей правильные результаты, когда ее аргумент меньше или равен n), то она возвращает более точное

приближение к iseven — функцию, выдающую правильные результаты вплоть до аргумента n 2.

Применение fix к этому генератору возвращает его неподвижную точку — функцию, возвращающую

правильный результат для любого входного значения n.

Есть, однако, одно важное отличие от бестипового языка: сама функция fix не может быть опреде-

лена в рамках простого типизированного лямбда-исчисления. Более того, в Главе 12 мы докажем, что

никакое выражение, способное привести к незавершающемуся вычислению, не может быть типизиро-

вано исключительно средствами простых типов.

Поэтому вместо того, чтобы определить fix как терм

нашего языка, мы просто добавляем его в качестве нового примитива, вместе с правилами вычисле-

ния, имитирующими поведение бестипового вомбинатора fix, и правилом типизации, отражающим его

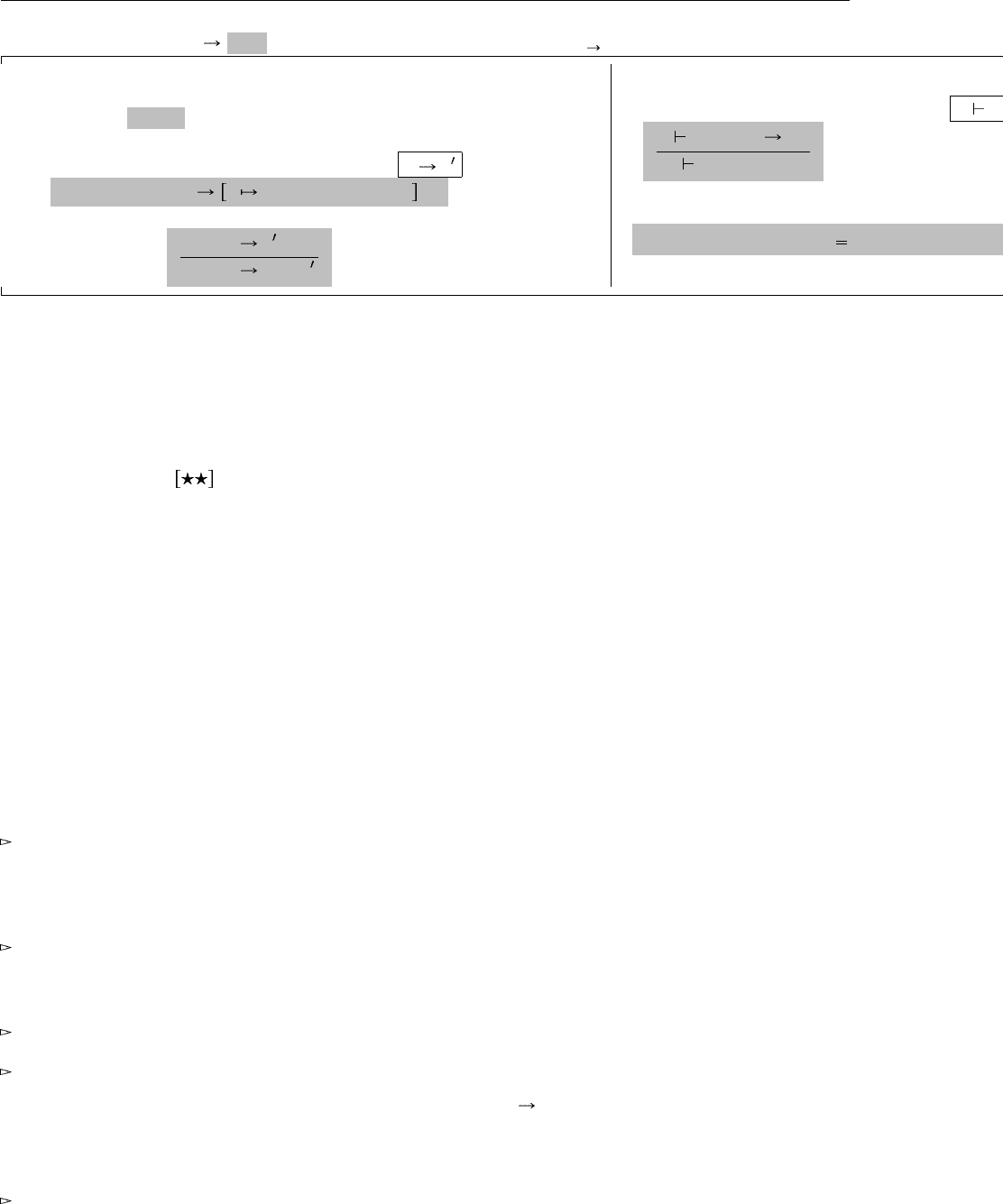
реальное использование. Эти правила изображениы на Рис. 11.12. (Сокращенная форма letrec будет

описана далее.)

Простое типизированное лямбда-исчисление с добавлением чисел и комбинатора fix давно уже

служит любимым объектом исследования для специалистов по языкам программирования, поскольку

В последующих главах — Главе 13 и Главе 20, — мы введем некоторые расширения в систему простых типов, возвра-

щающие нам способность определить fix средствами самой системы.

rev. 104

116 11.11. Рекурсия общего вида

fix Расширяет λ (9.1)

Новые синтаксические формы

t ::= . . . термы:

fix t неподвижная точка t

Новые правила вычисления t t

fix (λx:T

) x (fix (λx:T

)) t

(E-FixBeta)

fix t

(E-Fix)

Новые правила типизации Γ t : T

Γ t

: T

Γ fix t

: T

(T-Fix)

Новые производные формы

letrec x:T

in t

def

let x = fix (λx:T

) in t

Рис. 11.12. Общая рекурсия

это простейший язык, где имеет место множество тонких семантических явлений, например, полная

абстракция (Plotkin 1977, Hyland and Ong 2000, Abramsky, Jagadeesan and Malacaria 2000). Часто это

исчисление называют PCF .

Упражнение 11.11.1 : Определите при помощи fix функции equal, plus, times и factorial.

Как правило, конструкция fix используется для построения функций (в качестве неподвижных то-

чек функций, переводящих функции в функции), однако имеет смысл заметить, что тип T в правиле

T-Fix не обязательно должен быть функциональным. Иногда эта дополнительная гибкость оказы-

вается полезной. Например, она позволяет определить запись, состоящую из взаимно рекурсивных

функций, как неподвижную точку функции, работающей с записями (содержащими функции). Следу-

ющая реализация iseven использует вспомогательную функцию isodd; две эти функции определяются

как поля в записи, причем определение этой записи абстрагируется от записи ieio, и ее компоненты

используются для рекурсивных вызовов изнутри тел полей iseven и isodd.

ff = λieio :{ isev en : Nat -> Bool , isodd : Nat -> Bool }.

{ is even = λx: Nat .

if isze ro x then true

else ieio . isodd ( pred x),

isodd = λx : Nat .

if isze ro x then false

else ieio . is even ( pred x )};

ff : { isev en : Nat -> Bool , isodd : Nat -> Bool } ->

{ is even : Nat - >Bool , isodd : Nat - > Bool }

Неподвижная точка функции ff — запись из двух функций

r = fix ff ;

r : { i seven : Nat -> Bool , isodd : Nat -> Bool }

и обращение к первой из них дает нам саму функцию iseven:

is even = r . iseven ;

is even : Nat -> Bool

is even 7;

false : Bool

Способность породить неподвижную точку функции типа T T для любого T приводит к некоторым

неожиданным последствиям. В частности, оказывается, что каждый тип имеет хотя бы один терм-член.

Чтобы показать это, заметим, что для каждого типа T мы можем определить функцию diverge

di verge

= λ_: Unit . fix (λx: T .x );

di verge

: Unit -> T

rev. 104

11.12. Списки 117

Каждый раз, когда diverge

применяется к аргументу unit, мы получаем бесконечную последова-

тельность вычислений, где правило E-FixBeta применяется раз за разом, всегда давая один и тот же

терм. Получается, что для каждого типа T терм diverge

служит неопределенным элементом.

Последнее улучшение, которое мы рассмотрим — более удобный конкретный синтаксис для часто

встречающейся ситуации, когда требуется связать переменную с результатом рекурсивного определе-

ния. В большинстве высокоуровневых языков первое приведенное нами определение iseven было бы

записано примерно так:

le trec i seven : Nat -> Bool

λx : Nat .

if isze ro x then true

else if iszero ( pred x) then false

else iseven ( pred ( pred x))

is even 7;

false : Bool

Конструкцию рекурсивного связывания letrec несложно определить в качестве производной формы:

letrec x:T

in t

def

let x = fix (λx:T

) in t

Упражнение 11.11.2 : Перепишите свои определения функций plus, times и factorial из Упраж-

нения 11.11.1 через letrec вместо fix.

Более подробную информацию об операторах неподвижной точки можно найти у Клопа (Klop 1980)

и Винскеля (Winskel 1993).

11.12. Списки

Рассмотренные нами конструкции можно разделить на базовые типы, вроде Bool и Unit, и кон-

структоры типов вроде и , которые строят новые типы на основе старых. Еще один полезный

конструктор — List. Для каждого типа T, тип List T описывает списки конечной длины, состоящие

из элементов типа T.

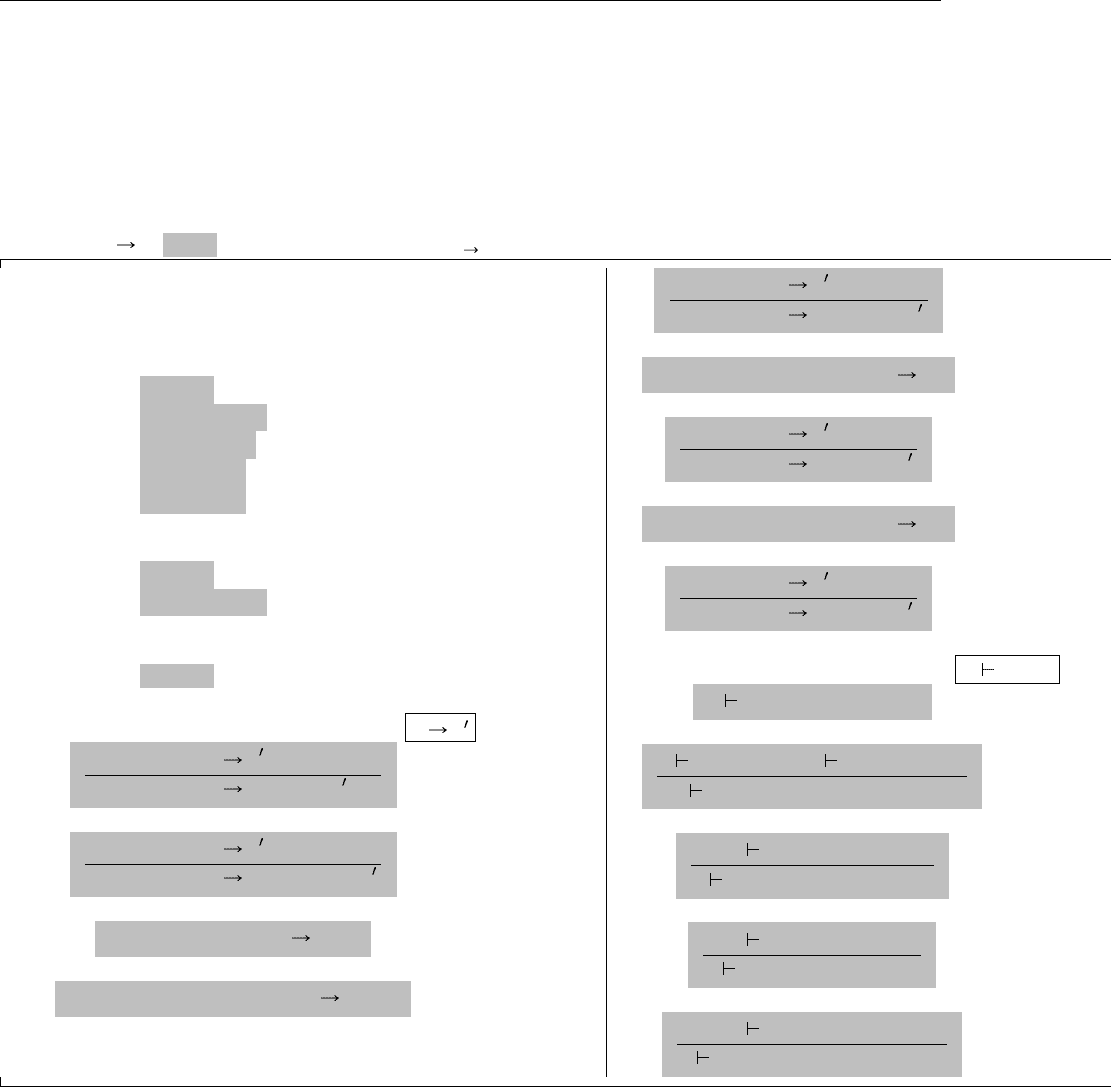
На Рис. 11.13 показаны синтаксис, семантика и правила типизации для списков. С точностью до

синтаксических расхождений (List T вместо T list и т. п.), а также того, что в нашем варианте все

синтаксические формы требуют явной аннотации типов, наши списки по существу совпалдают с име-

ющимися в ML и других функциональных языках. Пустой список (с элементами типа T) записывается

в виде nil[T]. Список, порождаемый при добавлении нового элемента t

(типа T) в начало списка t

записывается cons[T] t

. Голова и хвост списка t записываются head[T] t и tail[T] t. Булевский

предикат isnil[T] t выдает true тогда и только тогда, когда список t пуст.

Упражнение 11.12.1 : Убедитесь, что в простом типизированном лямбда-исчислении с булев-

скими значениями и списками выполняются теоремы о продвижении и сохранении.

Упражнение 11.12.2 : Представленный здесь синтаксис списков включает множество аннота-

ций, которые на самом деле не нужны, поскольку правила типизации легко могли бы вывести нужный

тип из контекста. (Эти аннотации предназначены для сравнения с кодированием списков в §23.4).

Можно ли избавиться от всех аннотаций?

Мы приняли «представление списков через head/tail/isnil» ради простоты. С точки зрения проектирования языков,

вероятно, правильнее было бы рассматривать списки как тип данных и обращаться к их компонентам через выражения

case, поскольку при этом больше программистских ошибок становятся ошибками типизации.

rev. 104

118 11.12. Списки

B List Расширяет λ (9.1) с булевскими значениями (8.1)

Новые синтаксические формы

t ::= . . . термы:

nil[T] пустой список

cons[T] t t конструктор списка

isnil[T] t проверка на пустой список

head[T] t голова списка

tail[T] t хвост списка

v ::= . . . значения:

nil[T] пустой список

cons[T] v v конструктор списка

T ::= . . . типы:

List T тип списков

Новые правила вычисления t t

cons[T] t

(E-Cons1)

cons[T] v

(E-Cons2)

isnil[T] (nil[T]) true

(E-IsnilNil)

isnil[T] (cons[T] v

) false

(E-IsnilCons)

isnil[T] t

(E-Isnil)

head[T] (cons[T] v

) v

(E-HeadCons)

head[T] t

(E-Head)

tail[T] (cons[T] v

) v

(E-TailCons)

tail[T] t

(E-Tail)

Новые правила типизации Γ t : T

Γ nil[T

] : List T

(T-Nil)

Γ t

: T

Γ t

: List T

Γ cons[T

] t

: List T

(T-Cons)

Γ t

: List T

Γ isnil[T

] t

: Bool

(T-Isnil)

Γ t

: List T

Γ head[T

] t

: T

(T-Head)

Γ t

: List T

Γ tail[T

] t

: List T

(T-Tail)

Рис. 11.13. Списки

rev. 104

Глава 12

Нормализация

В этой главе мы рассматриваем еще одно фундаментальное теоретическое свойство чистого про-

стого типизированного лямбда-исчисления: то, что вычисление правильно типизированной программы

гарантированно останавливается за конечное число шагов — т. е., каждый правильно типизированный

терм нормализуем.

В отличие от свойств типовой безопасности, рассмотренных нами ранее, свойство нормализации

не распространяется на полноразмерные языки программирования, поскольку эти языки почти всегда

расширяют простое типизированное лямбда-исчисление конструкциями вроде рекурсии общего вида

(§11.11) или рекурсивных типов (Глава 20), с помощью которых можно создавать незавершающиеся

программы. Однако понятие нормализации снова возникнет, уже на уровне типов, когда в §30.3 мы

будем обсуждать метатеорию Системы F

: в этой системе язык типов, по существу, содержит копию

простого типизированного лямбда-исчисления, и завершимость алгоритма проверки типов будет осно-

вываться на том, что операция «нормализации» на выражениях типов гарантированно завершается.

Еще одна повод изучать доказательства нормализации заключается в том, что это едва ли не самые

изящные — и захватывающие, — математические конструкции в литературе по теории типов, часто

(как в данном случае) с использованием базового метода доказательств через логические отношения.

Некоторым читателям будет проще пропустить данную главу; в последующих главах никаких слож-

ностей из-за этого не возникнет. (Полная таблица зависимостей между главами приведена на стр. 5.)

12.1. Нормализация для простых типов

Рассматриваемый здесь язык — простое типизированное лямбда-исчисление с единственным ба-

зовым типом A. Нормализация для этого исчисления не вполне тривиальна, поскольку при каждой

редукции терма могут создаваться множественные редексы в подтермах.

Упражнение 12.1.1 : В каком месте терпит неудачу попытка доказать нормализацию при помощи

простой индукции по размеру правильно типизированного терма?

Основная сложность здесь (как и во многих других доказательствах по индукции) в том, чтобы

найти достаточно сильное индуктивное предположение. С этой целью мы для каждого типа T опре-

деляем множество R

замкнутых термов типа T. Эти множества мы рассматриваем как предикаты и

пишем R

t вместо t R

Определение 12.1.2 • R

t тогда и только тогда, когда t завершается.

• R

t тогда и только тогда, когда t завершается, и, для всякого s, такого, что R

s ,

выполняется R

t s .

В этой главе изучается язык простого типизированного лямбда-исчисления (Рис. 9.1) с одним базовым типом A (11.1).

Иногда множества R

называют насыщенными множествами или множествами кандидатов на редуцируемость.

119

120 12.1. Нормализация для простых типов

Это определение дает нам требуемое усиление индуктивного предположения. Нам нужно доказать,

что завершаются все программы — т. е., все замкнутые термы базового типа. Однако замкнутые термы

базового типа могут содержать подтермы функционального типа, так что и об этих термах нужно кое-

что знать. Более того, недостаточно знать, что эти подтермы завершаются, поскольку при применении

нормализованной функции к нормализованному аргументу происходит подстановка, и эта подстановка

может привести к новым шагам вычисления. Таким образом, для термов функционального типа нам

нужно более сильное условие: они не только сами должны завершаться, но, будучи примененными к

завершающимся аргументам, они должны давать завершающиеся результаты.

Форма Определения 12.1.2 характерна для метода доказательств через логические отношения. (По-

скольку сейчас мы работаем только с одноместными отношениями, правильнее было бы сказать логи-

ческие предикаты.) Если мы хотим доказать, что некоторое свойство P выполняется для всех замкну-

тых термов типа A, мы с помощью индукции на типах доказываем, что все термы типа A обладают

свойством P , что все термы типа A A сохраняют свойство P , что все термы типа (A A) (A A)

сохраняют свойство сохранения свойства P , и так далее. Мы добиваемся этого через определение се-

мейства предикатов, проиндексированных типами. Для базового типа A этот предикат – просто P . Для

функциональных типов предикат говорит, что функция должна переводить значения, удовлетворяю-

щие предикату для входного типа, в значения, удовлетворяющие предикату для типа-результата.

При помощи этого определения мы проводим доказательство нормализации в два шага. Сначала

мы убеждаемся, что каждый элемент каждого множества R

нормализуем. Затем мы показываем, что

каждый правильно типизированный терм типа T является элементом R

Первый шаг непосредственно следует из определения R

Лемма 12.1.3 Если R

t , то t завершается.

Второй шаг разбит на две леммы. Сначала мы замечаем, что членство в R

сохраняется при вычис-

лении.

Лемма 12.1.4 Если t : T и t t , то R

t тогда и только тогда, когда R

t .

Доказательство: Индукция по структуре типа T. Во-первых, заметим, что t завершается тогда и

только тогда, когда завершается t . Если T A, доказывать больше нечего. С другой стороны, предпо-

ложим, что T T

для некоторых T

и T

. Для направления «слева направо» ( ) предположим,

что R

t , и что R

s для некоторого произвольного s : T

. По определению, имеем R

t s . Од-

нако t s t s, и отсюда, по предположению индукции для типа T

, получаем R

t s . Поскольку

это верно для любого s, определение R

дает нам R

t . Рассуждение в направлении «справа налево»

( ) проводится аналогично.

Теперь нам нужно доказать, что каждый терм типа T принадлежит множеству R

. Здесь индукция

будет проводиться по деревьям вывода типов (было бы странно, если бы какое-либо доказательство,

касающееся правильно типизированных термов, не содержало бы индукцию по деревьям вывода ти-

пов!). Единственная сложность здесь заключается в обработке варианта с λ-абстракцией. Поскольку

мы проводим индукцию, доказательство, что терм λx:T

принадлежит множеству R

, должно

сослаться на предположение индукции, утверждая, что t

принадлежит множеству R

. Однако R

определяется как множество замкнутых термов, в то время как переменная x может быть свободна в

, так что такая ссылка не работает.

Эта проблема решается с помощью стандартного приема: нужно найти подходящее обобщение пред-

положения индукции. Вместо того, чтобы доказывать утверждение о замкнутых термах, мы доказы-

ваем его обобщенную форму, включающую все замкнутые экземпляры открытого терма t.

Лемма 12.1.5 Если x

, . . . , x

t : T, а v

, . . . , v

— замкнутые значения типов T

, . . . , T

для каждого i, то R

, . . . x

t .

Доказательство: Индукция по дереву вывода утверждения x

, . . . , x

t : T. (Наиболее ин-

тересен вариант с абстракцией.)

Вариант T-Var: t x

T T

Утверждение леммы следует немедленно.

rev. 104