Пирс Б. Типы в языках программирования

Подождите немного. Документ загружается.

14.3. Исключения, сопровождаемые значениями 141

ра строк, если объявить T

exn

как тип-вариант:

exn

= <divideByZero: Unit,

overflow: Unit,

fileNotFound: String,

FileNotReadable: String,

...>

Такая схема позволяет обработчику различать виды исключений при помощи выражения case.

Кроме того, различные виды исключений могут нести различные типы дополнительной инфор-

мации: в исключениях вроде divideByZero ничего лишнего не требуется, вместе с fileNotFound

можно передать стрку, указывающую, что за файл пытались открыть, когда возникла ошибка, и

т. д.

Проблема с этой альтернативой в том, что она недостаточно гибкая, и требует, чтобы мы заранее

установили множество исключений, которые может породить любая программа (т. е., множество

тегов вариантного типа T

exn

). Программисты не могут определять исключения, тип которых от-

носится к конкретной программе.

4. Эту идею можно улучшить и дать возможность созадавать пользовательские типы исключений,

если объявить T

exn

расширяемым вариантным типом. Так поступает ML, где имеется един-

ственный расширяемый вариантный тип exn.

Объявление exception l of T в языке ML можно,

в нашей терминологии, понимать так: «убедиться, что l отличается от всех тегов, уже имею-

щихся в вариантном типе T

exn

и, начиная с этого момента, считать, что T

exn

равен <l

...l

,l:T>, где варианты от l

до t

были возможны до данного объявления».

Синтаксис ML для порождения исключений выглядит как raise l(t), где l — тег исключения,

определенный в текущей области видимости. Эту конструкцию можно понимать как сочетание

оператора навешивания тега и нашего обычного raise:

raise l(t)

def

raise (<l=t> as T

exn

)

Подобным образом, ML-евская конструкция try может быть без сахара записана как наша про-

стая try в сочетании с case.

try t with l(x)

def

try t with

λe:T

exn

. case e of

<l=x> => h

| _ => raise e

Конструкция case проверяет, помечено ли возникшее исключение тегом l. Если да, то она связы-

вает значение, переданное с исключением, с переменной x, и выполняет обработчик h. В против-

ном случае управление получает умолчательный вариант, который перезапускает исключение.

Исключение продолжит распространяться (возможно, при этом будучи несколько раз поймано и

перезапущено), пока оно либо не достигнет обработчика, желающего иметь с ним дело, либо не

окажется на самом верхнем уровне, и тогда вся программа завершается.

5. В Java вместо расширяемых вариантов для поддержки исключений, определяемых программи-

стом, используются классы. В языке есть встроенный класс Throwable; экземпляр Throwable или

любого из его подклассов можно употребить в предложении throw (аналогично нашему raise) или

try ...catch (как наше try ...with). Новые исключения можно объявлять, просто определяя

новые подклассы Throwable.

Существует ясное соответствие между таким механизмом обработки исключений и тем, который

принят в ML. Грубо говоря, объект-исключение в Java во время исполнения представляется через

тег, указывающий его класс (что прямо соответствует тегу расширяемого варианта в ML) плюс

запись переменных экземпляра (что соответствует дополнительной информации, помеченной этим

тегом).

Можно пойти дальше и сделать расширяемые вариантные типы вообще разрешенной языковой конструкцией, но

проектировщики ML предпочли просто считать exn особым случаем.

Поскольку форма exception связывает идентификатор, мы всегда можем сделать так, чтобы l отличался от уже

используемых в T

exn

тегов, произведя над ним при необходимости альфа-конверсию.

rev. 104

142 14.3. Исключения, сопровождаемые значениями

Исключения Java в некоторых отношениях идут дальше, чем в ML. Во-первых, существует есте-

ственный частичный порядок тегов исключений, определяемый порядком наследования подклас-

сов. Обработчик для исключения l будет перехватывать все исключения, имеющие класс l или

любой из подклассов l. Кроме того, Java различает исключения (подклассы встроенного класса

Exception — подкласса Throwable), которые программа может пожелать перехватывать и исправ-

лять, и ошибки (подклассы Error — это другой подкласс Throwable), обозначающие серьезные

неполадки, как правило, ведущие к остановке программы. Главное различие между ними состоит

в правилах проверки типов, которые требуют, чтобы методы явно объявляли, какие исключения

(но не ошибки) они могут породить.

Упражнение 14.3.1 : Описание расширяемых вариантных типов в альтернативе номер 4 недо-

статочно формально. Покажите, как сделать его точным.

Упражнение 14.3.2 : Мы упомянули, что исключения в Java (те, которые являются подклас-

сами Exception) отслеживаются несколько строже, чем исключения в ML (или те, что мы опре-

делили здесь): каждое исключение, которое может быть порождено методом, должно указываться

в типе этого метода. Расширьте свое решение Упражнения 14.3.1 так, чтобы тип, указываемый

для функции, содержал не только типы ее аргументов и результата, но и множество исключений,

которые в ней могут возникнуть. Докажите, что Ваша система соблюдает типовую безопасность.

Упражнение 14.3.3 : С помощью методов, подобных обсуждаемым в этой главе, можно фор-

мально определить многие другие конструкции. Читатели, знакомые с оператором «вызов с те-

кущим продолжением» (call-with-current-continuation, call/cc) из языка Scheme (см. Clinger,

Friedman and Wand 1995; Kelsey, Clinger and Rees 1998; Dybvig 1996; Friedman, Wand and Haynes

2001), могут получить удовольствие, попытавшись сформулировать правила типизации для типа

T-продолжений Cont T — т. е., типа продолжений, ожидающих аргумент типа T.

rev. 104

Часть III

Наследование

143

Глава 15

Наследование

Последние несколько глав мы занимались исследованием типового поведения нескольких языко-

вых конструкций в рамках простого типизированного лямбда-исчисления. В этой главе вводится более

существенное расширение: наследование (иногда называемое полиморфизмом через наследование). В

отличие от конструкций, изученных нами до сих пор, которые можно было сформулировать более или

менее независимо друг от друга, наследование существенно расширяет язык и затрагивает большинство

других языковых элементов нетривиальным образом.

Наследование, как правило, встречается в объектно-ориентированных языках, и часто рассматри-

вается как существенный элемент объектно-ориентированного стиля. Эта связь исследуется в Главе 18;

однако пока что мы описываем наследование в более экономном окружении, содержащем только функ-

ции и записи, поскольку уже здесь возникает большинство интересных вопросов, связанных с ним.

В §15.5 описывается сочетание наследования с некоторыми другими конструкциями, рассмотренными

нами в предыдущих главах. В последнем разделе главы (§15.6) мы исследуем более утонченную семан-

тику наследования, где его использование соответствует вставке преобразований типа в исполняемый

код.

15.1. Включение

Без наследования правила простого типизированного лямбда-исчисления могут быть раздражающе

жесткими. Требование системы типов, чтобы типы аргументов точно совпадали с областями определе-

ния функций, ведет к тому, что при проверке отвергаются многие программы, которые программисту

кажутся очевидно правильными. Вспомним, например, правило для применения функций:

Γ t

: T

Γ t

: T

Γ t

: T

(T-App)

Согласно этому правилу, правильно себя ведущий терм

(λr :{ x : Nat }. r . x) { x=0 ,y =1}

не поддается типизации, поскольку тип аргумента {x:Nat,y:Nat}, в то время как функция принимает

{x:Nat}. Ясно, однако, что для функции существенно только то, чтобы аргумент был записью с полем

x; имеются ли другие поля и каковы они, ей безразлично. Более того, это требование можно распознать

по типу функции — не нужно проверять ее тело и убеждаться, что поля помимо x не используются.

Передача аргумента типа {x:Nat,y:Nat} в функцию, ожидающую тип {x:Nat}, всегда безопасна.

Цель наследования в языке — улучшить правила типизации, так, чтобы термы вроде этого стали

разрешенными. Мы добиваемся этого, формализуя интуицию, что некоторые типы содержат больше

информации, чем другие: мы говорим, что S является подтипом T (записывается S<:T), имея в виду,

В оригинале используется слово subtyping, производное от термина subtype («подтип»), а не inheritance («наследова-

ние»). — прим. перев.

В этой главе изучается λ

, простое типизированное лямбда-исчисление с наследованием (Рис. 15.1) и записями

(Рис. 15.3); соответствующий интерпретатор на OCaml называется rcdsub. (В некоторых примерах также используются

числа; для их проверки требуется fullsub.)

145

146 15.2. Отношение наследования

что всякий терм типа S можно безопасно использовать в контексте, где ожидается тип T. Такую точку

зрения на наследование часто называют принципом безопасной подстановки.

Более простое интуитивное объяснение — считать, что S<:T означает «каждое значение, описы-

ваемое термином S, описывается также термином T», то есть, «элементы S являются подмножеством

элементов T». В §15.6 мы увидим, что иногда полезны другие, более сложные, интерпретации наследо-

вания, но такая семантика подмножеств достаточна в большинстве ситуаций.

Связь между отношением типизации и нашим новым отношением наследования обеспечивается

новым правилом типизации — так называемым правилом включения:

Γ t : S S <: T

Γ t : T

(T-Sub)

Это правило говорит, что, если S<:T, то всякий элемент S является также элементом T. Например,

если мы определим отношение наследования так, чтобы {x:Nat,y:Nat} <: {x:Nat}, то при помощи

правила T-Sub мы сможем вывести {x=0,y=1} : {x:Nat}, и, таким образом, присвоить тип нашему

исходному примеру.

15.2. Отношение наследования

Отношение наслодования формально описывается через набор правил вывода, заключением кото-

рых служат утверждения вида S<:T, что читается «S — подтип T» (или «T — надтип S»). Мы рассмотрим

каждую разновидность типов (типы функций, типы записей и т. д.) отдельно; для каждой из них мы

сформулируем правила, формализующие ситуации, когда можно разрешить использовать элементы

одного типа данной разновидности, при том, что ожидается другой тип.

Прежде, чем мы приступим к правилам для конкретных разновидностей типов, мы сделаем два

общих предположения: во-первых, отношение наследования должно быть рефлексивным:

S<:S (S-Refl)

а во-вторых, оно должно быть транзитивным:

S<:U U<:T

S<:T

(S-Trans)

Эти правила прямо следуют из нашей интуиции о безопасности подстановки.

Для типов записей мы уже убедились, что хотелось бы считать тип S { k

...k

} подти-

пом T { l

...l

}, если T содержит меньше полей, чем S. В частности, безопасно «забывать»

некоторые поля в конце типов записей. Эта интуиция отражена в так называемом правиле наследова-

ния в ширину:

i 1..n k

} <: {l

i 1..n

} (S-RcdWidth)

Может показаться странным, что «меньший» тип — подтип – содержит больше полей. Проще всего

это усвоить, если принять более либеральную точку зрения на типы записей, чем в §11.8, и считать,

что тип {x:Nat} описывает «множество записей, имеющих, по крайней мере, поле x типа Nat». Эле-

ментами этого типа являются значения вроде {x=3} и {x=5}, но, кроме того, еще и значения вроде

{x=3,y=100} и {x=3,a=true,b=true}. Подобным образом, тип {x:Nat,y:Nat} описывает записи, име-

ющие, по крайней мере, поля x и y, оба типа Nat. Значениями этого типа являются записи вроде

{x=3,y=100} и {x=3,y=100,z=true}, но не {x=3} и не {x=3,a=true,b=true}. Таким образом, множе-

ство значений, принадлежащих второму типу, является строгим подмножеством множества значений,

принадлежащих первому типу. Более длинный тип-запись представляет собой более жесткую — т. е.,

более информативную, — спецификацию, и, таким образом, описывает меньшее множество значений.

Правило наследования в ширину применимо только к типам записей, где типы общих полей совпа-

дают. Можно также позволить различаться типам отдельных полей, если типы каждого соответству-

ющего поля находятся в отношении наследования. Эту интуицию выражает правило наследования в

глубину:

для каждого i, S

<:T

i 1..n

} <: {l

i 1..n

}

(S-RcdDepth)

Следующее дерево вывода наследования показывает, с использованием правил S-RcdWidth

и S-RcdDepth, что тип вложенных записей {x:{a:Nat,b:Nat},y:{m:Nat}} является подтипом

rev. 104

15.2. Отношение наследования 147

{x:{a:Nat},y:{}}:

{a:Nat,b:Nat} <: {a:Nat}

S-RcdWidth

{m:Nat} <: {}

S-RcdWidth

{x:{a:Nat,b:Nat},y:{m:Nat}} <: {x:{a:Nat},y:{}}

S-RcdDepth

Если мы хотим с помощью S-RcdDepth уточнить тип только одного поля записи (а не всех полей, как

в предыдущем примере), для остальных полей можно получить тривиальные отношения наследования

через правило S-Refl:

{a:Nat,b:Nat} <: {a:Nat}

S-RcdWidth

{m:Nat} <: {m:Nat}

S-Refl

{x:{a:Nat,b:Nat},y:{m:Nat}} <: {x:{a:Nat},y:{m:Nat}}

S-RcdDepth

При сочетании наследования в ширину и в глубину можно также использовать правило транзитивности.

Например, можно получить надтип, повысив тип одного поля и отбросив другое:

{x:{a:Nat,b:Nat}, y:{m:Nat}} : {x:{a:Nat,b:Nat}}

S-RcdWidth

{a:Nat,b:Nat} <: {a:Nat}

S-RcdWidth

{x:{a:Nat,b:Nat}} <: {x:{a:Nat}}

S-RcdDepth

{x:{a:Nat,b:Nat},y:{m:Nat}} <: {x:{a:Nat}}

S-Trans

Последнее наше правило для наследования записей происходит из наблюдения, что порядок

полей в записи не оказывает никакого влияния на то, какое ее использование безопасно, поскольку

единственная операция, которую мы можем производить с записью, когда она создана — т. е., проекция

ее полей, — нечувствительна к порядку полей.

j 1..n

}является перестановкой{l

i 1..n

}

j 1..n

} <: {l

i 1..n

}

(S-RcdPerm)

Например, согласно правилу S-RcdPerm, тип {c:Top,b:Bool,a:Nat} является подтипом

{a:Nat,b:Bool,c:Top}, и наоборот. (Отсюда следует, что отношение наследования не будет ан-

тисимметрично.)

С помощью S-RcdPerm совместно с S-RcdWidth и S-Trans можно отбрасывать поля в середине

записи, не только в конце.

Упражнение 15.2.1 : Нарисуйте дерево вывода, показывающее, что {x:Nat,y:Nat,z:Nat} является

подтипом {y:Nat}.

Каждое из правил S-RcdWidth, S-RcdDepth и S-RcdPerm дает нам отдельную степень свободы

при работе с записями. В целях обсуждения имеет смысл оставить их в виде отдельных правил. В

частности, существуют языки, где разрешается только часть из них. Например, большинство вариантов

исчисления объектов Абади и Карделли (Abadi and Cardelli 1996) опускают наследование в глубину.

Однако в целях реализации полезно сочетать эти правила в одном макроправиле, которое обрабатывает

все три вида наследования сразу. Это правило обсуждается в следующей главе (см. стр. 168).

Поскольку мы работаем с языком высшего порядка, где в качестве аргументов в функцию могут

передаваться не только числа и записи, но и другие функции, требуется также дать правило насле-

дования для функциональных типов — т. е., мы должны указать, в каких обстоятельствах можно без

опаски использовать функцию одного типа там, где ожидается функция другого типа.

<: S

<: T

(S-Arrow)

Заметим, что смысл отношения наследования обращен (контравариантен) для типов аргументов в ле-

вой предпосылке, но имеет одно и то же направление (ковариантен) для типов результатов и для самих

функциональных типов. Интуиция состоит в том, что, имея функцию f типа S

, мы знаем, что

f принимает аргументы типа S

; ясно, что f может также принять аргумент типа T

, где T

— любой

подтип S

. Тип f сообщает нам также, что она возвращает элементы типа S

; мы имеем право считать,

rev. 104

148 15.2. Отношение наследования

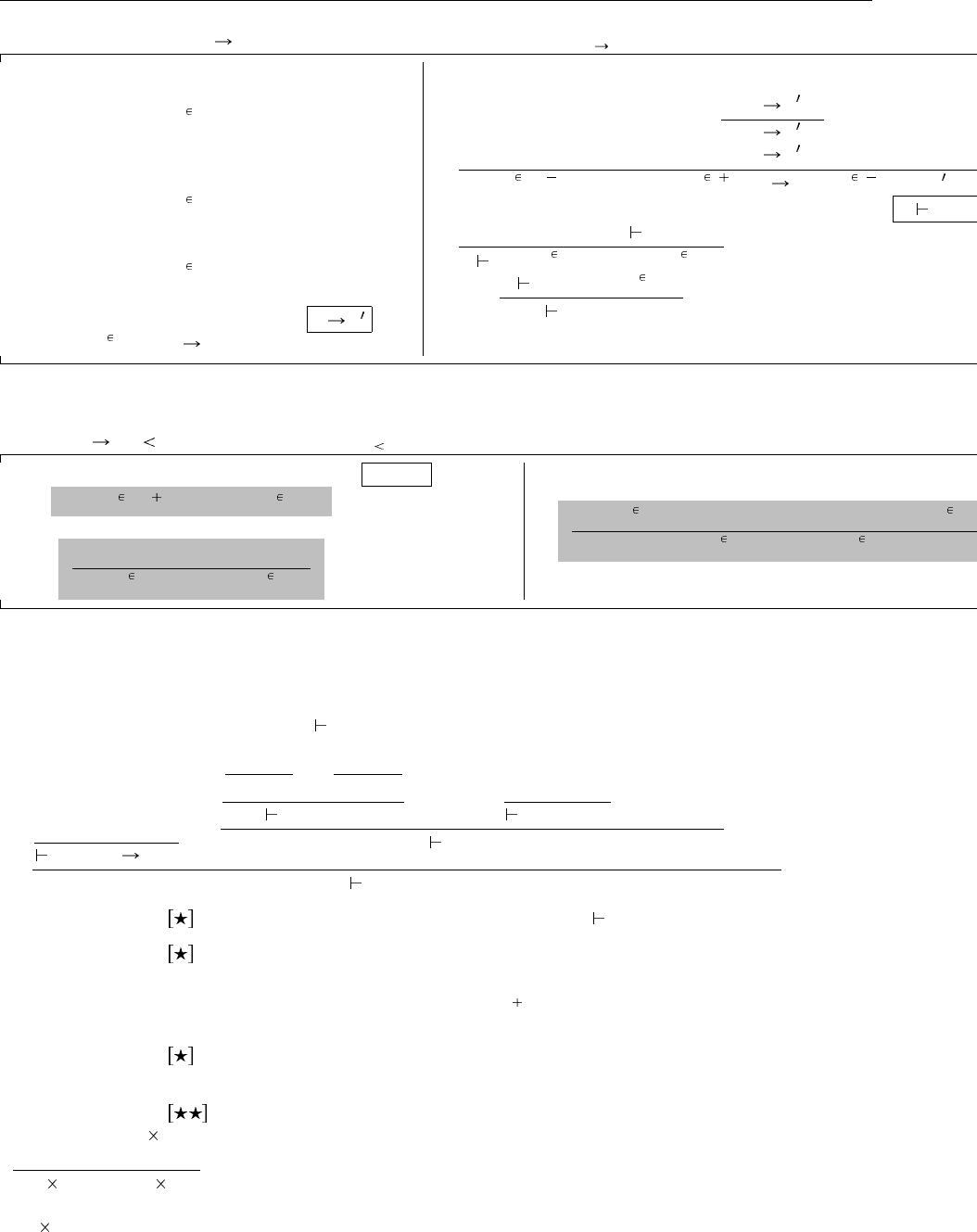
<: Top Основано на λ (9.1)

Синтаксис

t ::= термы:

x переменная

λx:T.t абстракция

t t применение

v ::= значения:

λx:T.t значение-абстракция

T ::= типы:

Top максимальный тип

T T тип функций

Γ ::= контексты:

пустой контекст

Γ, x:T связывание термовой переменной

Вычисление t t

(E-App1)

(E-App2)

(λ x:T

) v

x v

(E-AppAbs)

Наследование S <: T

S<:S (S-Refl)

S<:U U<:T

S<:T

(S-Trans)

S <: Top (S-Top)

<: S

<: T

(S-Arrow)

Типизация Γ t : T

x : T Γ

Γ x : T

(T-Var)

Γ, x:T

Γ λx:T

: T

(T-Abs)

Γ t

: T

Γ t

: T

Γ t

: T

(T-App)

Γ t : S S <: T

Γ t : T

(T-Sub)

Рис. 15.1. Простое типизированное лямбда-исчисление с наследованием (λ

)

что они принадлежат также T

, где T

— любой надтип S

. То есть, любая функция f типа S

может также рассматриваться как функция типа T

Другая возможная точка зрения состоит в том, что безопасно разрешить использовать функцию

типа S

в любом контексте, где ожидается тип T

, если ни один аргумент, который может

быть передан в функцию, ее не смутит (T

<: S

), и ни один ее результат не окажется неожиданным

для контекста вызова (S

<: T

Наконец, удобно иметь тип — надтип всех остальных типов. Мы вводим новую типовую контанту

Top и правило, делающее Top наибольшим элементом в отношении наследования:

S <: Top (S-Top)

Тип Top подробнее обсуждается в §15.4.

С формальной точки зрения, отношение наследования есть наименьшее отношение, замкнутое от-

носительно данных нами правил. Для удобства ссылок, на Рис. 15.1, 15.2 и 15.3 приведено полное опре-

деление простого типизированного лямбда-исчисления с записями и наследованием, причем синтакси-

ческие формы и правила, введенные нами в этой главе, выделены серым. Заметим, что присутствие

правил рефлексивности и транзитивности означает, что отношение наследования является предпоряд-

ком, однако, из-за правила перестановки полей в записи, частичным порядком оно не является: имеется

много пар различных типов, где каждый член — подтип другого.

Завершая обсуждать отношение наследования, давайте убедимся, что теперь мы можем присвоить

тип терму-примеру, с которого началась эта глава. Воспользуемся следующими сокращениями, чтобы

поместиться на странице:

def

λr:{x:Nat}. r.x Rx

def

{x:Nat}

def

{x=0,y=1} Rxy

def

{x:Nat,y:Nat}

rev. 104

15.2. Отношение наследования 149

{} Расширяет λ (9.1)

Новые синтаксические формы

t ::= . . . термы:

i 1..n

} запись

t.l проекция

v ::= . . . значения:

i 1..n

} запись-значение

T ::= . . . типы:

i 1..n

} тип записей

Новые правила вычисления t t

i 1..n

}.l

(E-ProjRcd)

.l t

(E-Proj)

i 1..j 1

, l

k j 1..n

} {l

i j 1

, l

k j 1..n

}

(E-Rcd)

Новые правила типизации Γ t : T

для каждого i, Γ t

: T

Γ {l

i 1..n

} : {l

i 1..n

}

(T-Rcd)

Γ t

: {l

i 1..n

}

Γ t

: T

(T-Proj)

Рис. 15.2. Записи (совпадает с Рис. 11.7)

{} : Расширяет λ

(15.1) и правила для простых записей (15.2)

Новые правила наследования S <: T

i 1..n k

} <: {l

i 1..n

} (S-RcdWidth)

для каждого i, S

<:T

i 1..n

} <: {l

i 1..n

}

(S-RcdDepth)

j 1..n

} является перестановкой {l

i 1..n

}

j 1..n

} <: {l

i 1..n

}

(S-RcdPerm)

Рис. 15.3. Записи и наследование

Предполагая обычные правила типизации для числовых констант, мы можем построить такое дерево

вывода для утверждения типизации f xy : Nat:

f : Rx Nat

0 : Nat 1 : Nat

xy : Rxy

T-Rcd

Rxy <: Rx

S-RcdWidth

xy : Rx

T-Sub

f xy : Nat

T-App

Упражнение 15.2.2 : Является ли приведенное дерево вывода для f xy : Nat единственным?

Упражнение 15.2.3 : (1) Сколько различных подтипов имеет {a:Top,b:Top}? (2) Можете ли Вы

найти бесконечную нисходящую цепочку в отношении наследования — то есть, бесконечную последо-

вательность типов S

, S

, и т. д., такую, что каждый S

i 1

является подтипом S

? (3) Возможно

ли найти бесконечную восходящую цепочку?

Упражнение 15.2.4 : Существует ли тип, являющийся подтипом любого другого типа? Суще-

ствует ли функциональный тип, являющийся надтипом любого другого функционального типа?

Упражнение 15.2.5 : Допустим, что мы расширили наше исчисление конструктором типов-

произведений T

, как описано в §11.6. Естественно добавить правило наследования

<: T

(S-ProdDepth)

соответствующее S-RcdDepth для записей. Правильно ли будет добавить также S-ProdWidth?

<: T

(S-ProdWidth)

rev. 104

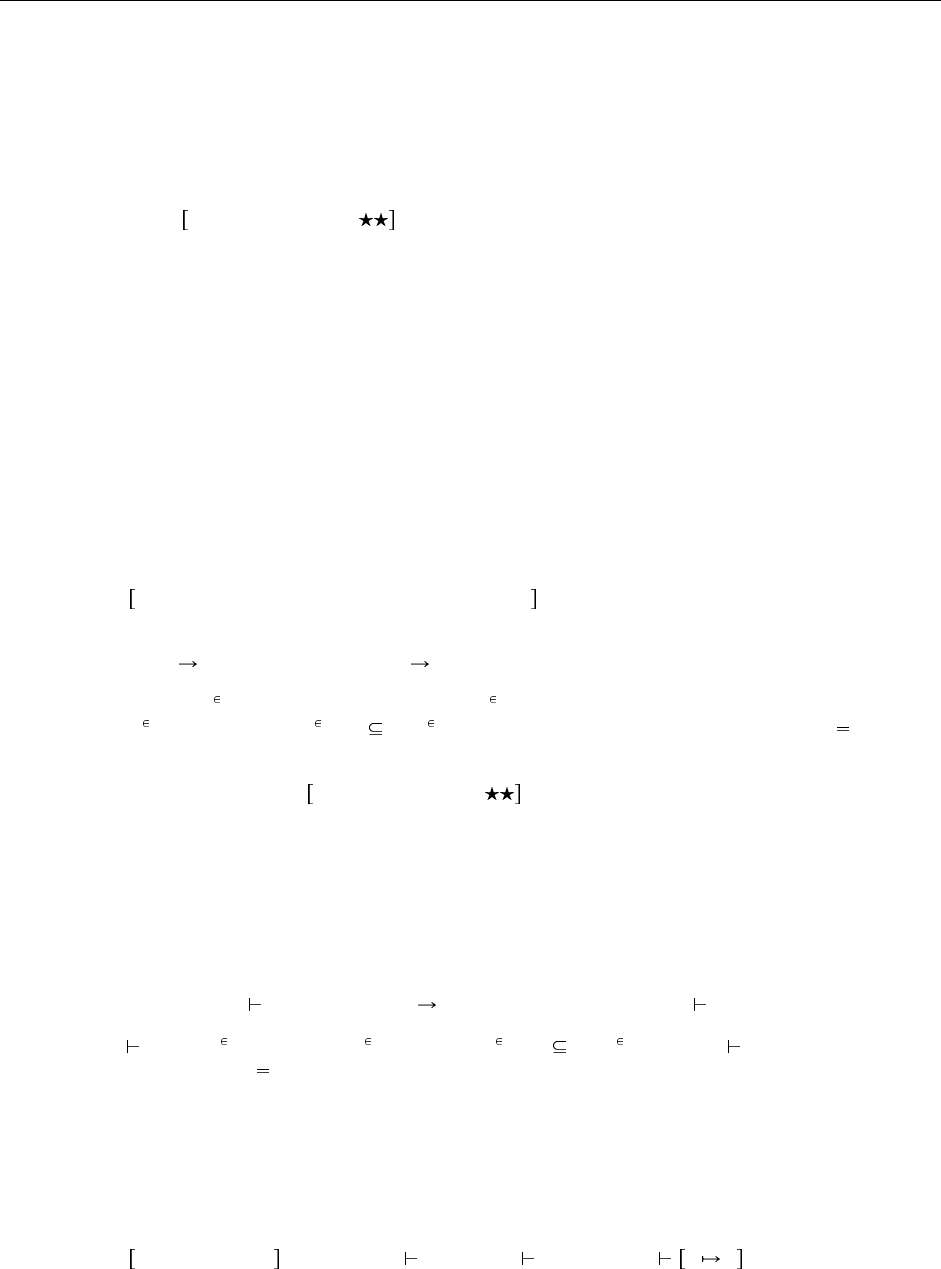
150 15.3. Свойства наследования и типизации

15.3. Свойства наследования и типизации

Определив формально лямбда-исчисление с наследованием, мы должны теперь проделать некото-

рую работу, чтобы убедиться, что это определение имеет смысл — в частности, что теоремы о сохра-

нении и продвижении для простого типизированного лямбда-исчисления продолжают выполняться,

когда в язык добавлено наследование.

Упражнение 15.3.1 Рекомендуется, : Прежде, чем читать дальше, попробуйте предсказать,

где в доказательствах могут возникнуть сложности. В частности, представим, что мы ошиблись

при определении наследования и добавили к имеющимся у нас еще одно, неверное правило наследова-

ния. Какие свойства системы могут при этом потеряться? С другой стороны, предположим, что

мы забыли определить одно из правил наследования — могут ли при этом исчезнуть какие-либо

свойства?

Вначале мы формулируем одно ключевое свойство отношения наследования — аналог леммы об об-

ращении для отношения типизации в простом типизированном лямбда-исчислении (Лемма 9.3.1). Если

нам известно, что S является подтипом функционального типа, то лемма об обращении с наследовани-

ем говорит, что и сам S должен быть функциональным типом; более того, она утверждает, что левые

параметры двух типов должны быть (контравариантно) родственны, а также и правые параметры

(ковариантно). Подобные соображения работают и в случае, когда известно, что S является подти-

пом типа записей: мы знаем, что S содержит больше полей (S-RcdWidth) в произвольном порядке

(S-RcdPerm), и типы общих полей должны быть связаны отношением наследования (S-RcdDepth).

Лемма 15.3.2 Обращение отношения наследования :

1. Если S <: T

, то S имеет вид S

, причем T

<: S

и S

<: T

2. Если S <: {l

i 1..n

}, то S имеет вид {k

j 1..m

}, причем содержит по крайней мере метки

полей {l

i 1..n

} — т. е., {l

i 1..n

} {k

j 1..m

}, и для каждой общей метки поля l

, S

Доказательство: Упражнение Рекомендуется, .

Чтобы доказать, что типы сохраняются при вычислении, мы начинаем с леммы об обращении от-

ношения типизации (ср. с Леммой 9.3.1 для простого типизированного лямбда-исчисления). Вместо

того, чтобы сформулировать эту лемму в самой общей форме, мы здесь приводим только те частные

случаи, которые оказываются необходимы для доказательства теоремы о сохранении, (Общую фор-

му можно получить путем исследования алгоритмического отношения типизации в следующей главе,

Определение 16.2.2).

Лемма 15.3.3 1. Если Γ λx:S

. s

: T

, то T

<: S

, и Γ, x:S

: T

2. Если Γ {k

a 1..m

} : {l

i 1..n

}, то {l

i 1..n

} {k

a 1..m

}, и Γ s

: T

для каждой

общей метки поля k

Доказательнство: Несложная индукция по деревьям вывода типов, с использованием Леммы 15.3.2

для правила T-Sub.

Затем нам требуется лемма о подстановке для отношения типизации. Формулировка леммы от-

стается неизменной по сравнению с простым типизированным лямбда-исчислением (Лемма 9.3.8), и

доказательство также почти совпадает.

Лемма 15.3.4 Подстановка : Если Γ, x:S t : T и Γ s : S, то Γ x s t : T.

Доказательство: Индукция по деревьям вывода типов. Требуется рассмотреть новые варианты для

правил T-Sub и для правил типизации записей T-Rcd и T-Proj, где очевидным образом используется

предположение индукции. В остальном доказательство такое же, как для 9.3.8.

rev. 104