Пирс Б. Типы в языках программирования
Подождите немного. Документ загружается.


16.2. Алгоритмическое отношение типизации 171
Более интересный случай представляет собой правило применения T-App. Здесь у нас имеется два
подвывода, и каждый из них может кончаться на T-Sub. Сначала рассмотрим случай, когда правило
применения встречается в конце левого подвывода.
.
.
.
Γ s
1
: S
11
S
12
.
.
.
S
11
S
12
<: T
11
T
12
Γ s
1
: T
11
T
12
T-Sub
.
.
.
Γ s
2
: T
11
Γ s
1
s
2
: T
12
T-App
Учитывая результаты из предыдущего раздела, мы имеем право предположить, что последним прави-
лом в выводе S
11
S
12
<: T
11
T
12
не будет ни S-Refl, ни S-Trans. А исходя из вида его заключения,
таким правилом может быть только S-Arrow.
.
.
.
Γ s
1
: S
11
S
12
.
.
.
T
11
<: S
11
.
.
.
S
12
<: T
12
S
11
S
12
<: T
11
T
12
S-Arrow
Γ s
1
: T
11
T
12
T-Sub
.
.
.
Γ s
2
: T
11
Γ s
1
s
2
: T
12
T-App
Перестройка правил с уничтожением T-Sub приводит к интересному результату.
.
.
.
Γ s
1
: S
11
S
12
.
.
.
Γ s
2
: T
11
.
.
.
T
11
<: S
11
Γ s
2
: S
11
T-Sub
Γ s
1
s
2
: S
12
T-App
.
.
.
S
12
<: T
12
Γ s
1
s
2
: T
12
T-Sub
Правый подвывод исходного экземпляра S-Arrow сдвинут вниз в корень дерева, где новый экземпляр
T-Sub повышает тип всего терма-применения. С другой стороны, левый подвывод передвинут вверх
по дереву, туда, где определяется тип аргумента s
2
.
Предположим теперь, что экземпляр T-Sub, подлежащий перестройке, расположен в конце правого
подвывода дерева, завершающегося правилом T-App.
.
.
.
Γ s
1
: T
11
T
12
.
.
.
Γ s
2
: T
2
.
.
.
T
2
<: T
11
Γ s
2
: T
11
T-Sub
Γ s
1
s
2
: T
12
T-App
Единственное, что мы можем сделать с таким экземпляром T-Sub — передвинуть его в левый подвывод,
отчасти обращая при этом предыдущее преобразование.
.
.
.
Γ s
1
: T
11
T
12
.
.
.
T
2
<: T
11
T
12
<: T
12
S-Refl
T
11
T
12
<: T
2
T
12
S-Arrow
Γ s
1
: T
2
T
12
T-Sub
.
.
.
Γ s
2
: T
2
Γ s
1
s
2
: T
12
T-App
rev. 104

172 16.2. Алгоритмическое отношение типизации
Итак, как мы видим, экземпляр правила включения, который повышает тип результата терма-
применения, может быть передвинут вниз через правило T-App, но экземпляр, где включение исполь-
зуется для согласования между типом аргумента функции и типом области ее определения, уничтожить
нельзя. Можно передвинуть его из одной предпосылки в другую — мы можем повысить тип аргумента,
чтобы он соответствовал типу области определения, либо мы можем повысить тип функции (понизив
тип ее аргумента) так, чтобы она ожидала аргумент, который мы на самом деле собираемся ей скор-
мить, — но вообще избавиться от правила включения здесь невозможно. Это наблюдение в точности
соответствует нашей интуиции, что такое использование T-Sub существенно увеличивает мощность
системы.
Еще один случай, требующий рассмотрения — когда последним правилом в дереве вывода служит
включение, а его непосредственный подвывод также завершается правилом включения. В этом случае
два подряд экземпляра включения можно слить в один — т. е., всякий вывод вида
.
.
.
Γ s : S
.
.
.
S <: U
Γ s : U
T-Sub
.
.
.
U <: T
Γ s : T
T-Sub
можно переписать как
.
.
.
Γ s : S
.
.
.
S <: U
.
.
.
U <: T
S <: T
S-Trans
Γ s : T
T-Sub
Упражнение 16.2.1 : Для завершения эксперимента, покажите, как производить подобное пе-
реупорядочение правил в выводах, где правило T-Sub используется перед T-Rcd либо перед T-Proj.
Применяя эти преобразования раз за разом, мы можем привести произвольное дерево вывода типа
к форме особого вида, где T-Sub встречается только в двух местах: в конце правого подвывода для
термов-применений, и в самом конце дерева. Более того, если мы просто отбросим экземпляр T-Sub в
самом конце, никакого особенного вреда это не принесет: у нас по-прежнему останется дерево вывода,
присваивающее тип тому же самому терму — единственная разница, что тип, присваиваемый терму,
будет меньше (то есть лучше!). Остается только одно место, термы-применения, где все еще могут
встречаться экземпляры правила включения. Чтобы учесть эти случаи, мы заменяем правило для
применений несколько более мощной версией,
Γ t
1
: T
11
T
12
Γ t
2
: T
2
T
2
<: T
11
Γ t
1
t
2
: T
12
уже содержащей использование включения как одну из предпосылок. Каждый подвывод вида
применение-с-включением-перед-ним можно заменить на экземпляр этого правила, и в результате у
нас никаких случаев использования T-Sub не останется. Более того, расширенное правило применения
управляется синтаксисом: форма терма в его заключении не перекрывается с остальными правилами.
Такое преобразование дает нам набор правил типизации, управляемый синтаксисом, и при этом при-
сваивающий типы тем же самым термам, что и исходные правила типизации. Новые правила сведены в
следующее определение. Как и в случае с алгоритмическими правилами наследования, мы записываем
алгоритмическое отношение типизации с измененным знаком штопора, Γ t : T, чтобы не путать
его с декларативным отношением.
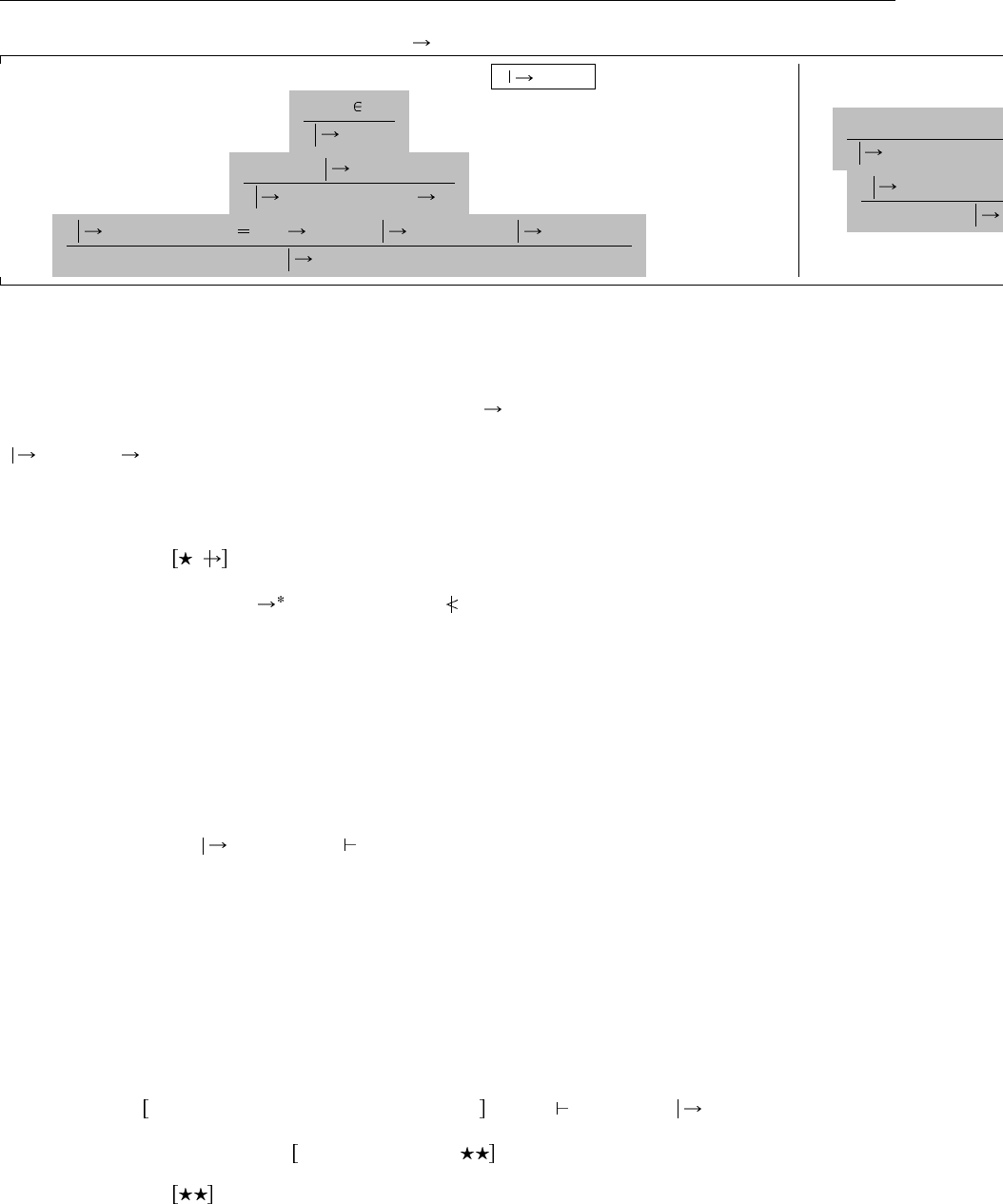
Определение 16.2.2 Отношение алгоритмической типизации есть наименьшее отношение, замкнутое
относительно правил с Рис. 16.3. Предпосылка T
1
T
11
T
12
в правиле для применений — просто
rev. 104
16.2. Алгоритмическое отношение типизации 173
{} <:
Алгоритмическая типизация Γ t : T
x:T Γ
Γ x : T
(TA-Var)
Γ, x:T t
2
: T
2
Γ λx:T
1
.t
2
: T
1
T
2
(TA-Abs)
Γ t
1
: T
1
T
1
T
11
T
12
Γ t
2
: T
2
T
2
<: T
11
Γ t
1
t
2
: T
12
(TA-App)
для каждого i Γ t
i
: T
i
Γ {l
1
=t
1
...l
n
=t
n
} : {l
1
:T
1
...l
n
:T
n
}
(TA-Rcd)
Γ t
1
: R
1
R
1
{l
1
:T
1
...l
n
:T
n
}
Γ t
1
.l
i
: T
i
TA-Proj
Рис. 16.3. Алгоритмическая типизация
явное напоминание о последовательности операций при проверке типов: мы сначала вычисляем тип
T
1
для t
1
; затем проверяем, что t
1
имеет вид T
11
T
12
, и т. д. Правило работало бы точно в
тех же случаях, если бы мы исключили эту предпосылку, а вместо первой предпосылки написали бы
Γ t
1
: T
11
T
12
. То же замечание верно и для TA-Proj. Кроме того, предпосылка о наследовании
в правиле для применений записана с измененным знаком штопора; поскольку мы знаем, что алго-
ритмическое представление наследования эквивалентно декларативному, такой выбор — дело вкуса.
Упражнение 16.2.3 : Покажите, что тип, присваиваемый терму алгоритмическими прави-
лами, может уменьшиться при вычислении, т. е., найдите два терма s и t с алгоритмическими
типами S и T, такие, что s t и T <: S, но S : T.
Нам еще нужно формально проверить, что алгоритмические правила типизации соответствуют ис-
ходным декларативным правилам. (Преобразования деревьев вывода, перечисленные нами выше, слиш-
ком неформальны, чтобы считаться доказательством. Их можно превратить в такое доказательство, но
такая работа будет слишком долгой и трудоемкой: проще, как обычно, построить индукцию по деревьям
вывода.) Как и в случае с наследованием, мы доказываем, что алгоритмические правила корректны и
полны по отношению к исходным декларативным правилам.
Свойство корректности имеет прежний вид: каждое утверждение о типизации, выводимое алгорит-
мическими правилами, выводимо также и декларативными.
Теорема 16.2.4 Если Γ t : T, то Γ t : T
Доказательство: Прямолинейная индукция по алгоритмическим деревьям вывода типов.
С другой стороны, полнота выглядит немного иначе. Обыкновенное отношение типизации способно
присвоить терму множество типов, в то время как алгоритмическое присваивает не более одного (это
нетрудно проверить). Таким образом, прямой аналог Теоремы 16.1.5 явно неверен. Вместо этого мы
можем показать, что когда терм t имеет по обыкновенным правилам типизации тип T, по алгоритми-
ческим правилам у него всегда есть тип S, который лучше T, в смысле, что S <: T. Другими словами,
алгоритмические правила присваивают каждому терму его наименьший (минимальный) тип. Теорему
о полноте часто называют теоремой о Наименьшем Типе, поскольку (вместе с Теоремой 16.2.4) она
означает, что всякий типизируемый терм в декларативной системе имеет минимальный тип.
Теорема 16.2.5 Полнота, или Наименьшие Типы Если Γ t : T, то Γ t : S для некоторого
S <: T.
Доказательство: Упражнение Рекомендуется, .
Упражнение 16.2.6 : Если мы отбросим правило наследования для функций S-Arrow, а осталь-
ные декларативные правила наследования и типизации оставим как есть, будет ли система по-
прежнему обладать свойством наименьшего типа? Если да, докажите. Если нет, приведите пример
типизируемого терма, у которого отсутствует минимальный тип.
rev. 104

174 16.3. Пересечения и объединения
16.3. Пересечения и объединения
Проверка типов выражений с несолькими возможными результатами, скажем, условных выражений
или case, в языке с наследованием требует некоторых дополнительных хитростей. Вспомним, например,
декларативное правило типизации для условных выражений:
Γ t
1
: Bool Γ t
2
: T Γ t
3
: T
Γ if t
1
then t
2
else t
3
: T
(T-If)
Правило требует, чтобы тип обеих ветвей был одинаков, и присваивает этот тип условному выражению
в целом. Однако когда в системе имеется правило включения, может быть много способов дать обеим
ветвям один и тот же тип. Например,
if true then {x= true ,y = false } else { x = false , z= true }
имеет тип {x:Bool}, поскольку ветвь then имеет минимальный тип {x:Bool,y:Bool}, который можно
поднять до {x:Bool} с помощью T-Sub, а ветвь else подобным же образом имеет минимальный тип
{x:Bool,z:Bool}, поднимаемый также до {x:Bool}. Тот же самый терм имеет и типы {x:Top} и {}
— в сущности, любой тип, одновременно являющийся надтипом {x:Bool,y:Bool} и {x:Bool,z:Bool}.
Следовательно, минимальным типом всего условного выражения является минимальный общий надтип
{x:Bool,y:Bool} и {x:Bool,z:Bool} — т. е., {x:Bool}. В общем случае, чтобы вычислить минимальный
тип произвольного условного выражения, мы должны найти минимальные типы его ветвей then и else,
а затем найти их минимальный общий надтип. Такой тип часто называется объединением типов ветвей,
поскольку он соответствует обычному объединению (точной верхней грани) двух элементов в частичном
порядке.
Определение 16.3.1 Тип J называется объединением пары типов S и T, что записывается S T J,
если S <: J, T <: J, и для всех типов U, если S <: U и T <: U, то J <: U. Подобным образом, тип M
называется пересечением S и T, что обозначается S T M, если M <: S, M <: T, и для всякого типа
L, если L <: S и L <: T, то L <: M.
В зависимости от того, как в конкретном языке с наследованием определено отношение наследова-
ния, может быть или не быть верно, что для всякой пары типов существует объединение. Говорят, что
отношение наследования обладает объединениями, если для всяких S и T существует некоторый тип J,
являющийся объединением S и T. Подобным образом, отношение наследования обладает пересечениями
если для каждого S и T имеется некоторый M — пересечение S и T.
Отношение наследования, рассматриваемое нами в этом разделе,
1
обладает объединениями, но не
пересечениями. Например, у типов {} и Top Top вообще нет общих подтипов, так что нет и наибольше-
го общего подтипа. Однако выполняется несколько более слабое условие. Мы говорим, что пара типов
S и T ограничена снизу, если имеется какой-либо тип L, такой, что L <: S и L <: T. Отношение насле-
дования обладает ограниченными пересечениями, если для каждой пары ограниченных снизу типов S
и T имеется M — пересечение S и T.
Объединения и пересечения не обязательно уникальны. Например, {x:Top,y:Top} и {y:Top,x:Top}
оба являются объединениями пары типов {x:Top,y:Top,z:Top} и {x:Top,y:Top,w:Top}. Однако два
раличных объединения (или пересечения) одной и той же пары типов всегда являются подтипами друг
друга.
Утверждение 16.3.2 1. Для каждой пары типов S и T имеется тип J, такой что S T J.
2. Для каждой пары типов S и T, имеющих общий подтип, имеется тип M, такой, что S T M.
Доказательство: Упражнение Рекомендуется, .
С помощью операции объединения мы можем задать алгоритмическое правило для выражений if
в системе с наследованием:
Γ t
1
: T
1
T
1
Bool Γ t
2
: T
2
Γ t
3
: T
3
T
2
T
3
T
Γ if t
1
the t
2
else t
3
: T
(TA-If)
1
А именно, отношение, определенное на Рис. 15.1 и 15.3, и расширенное типом Bool. В отношении наследования Bool
ведет себя просто: в декларативное отношение наследования никаких связанных с ним правил не добавляется, так что
его единственным надтипом является Top.
rev. 104
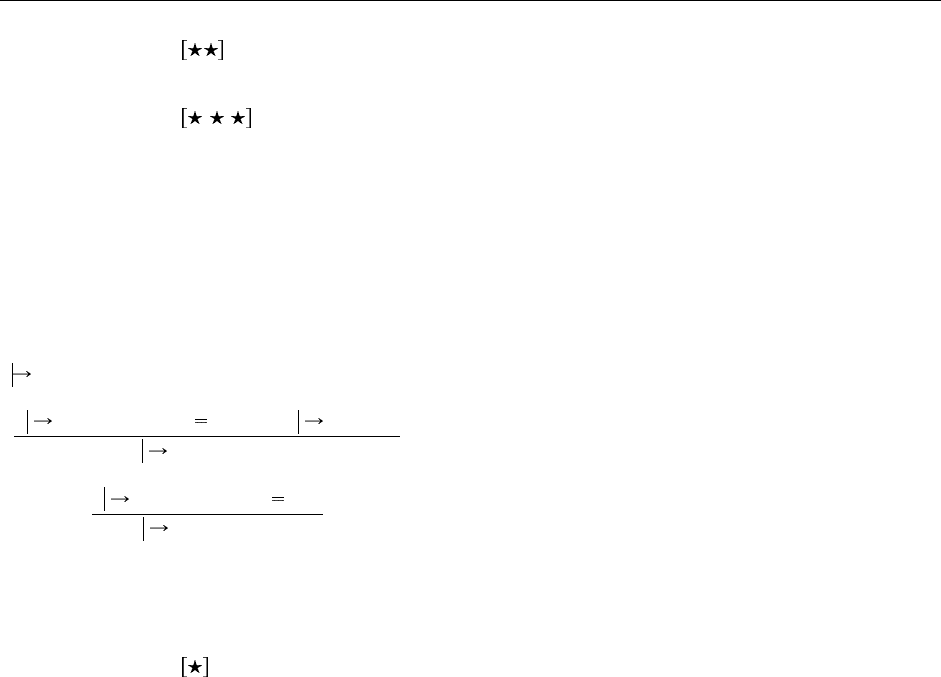
16.4. Алгоритмическая типизация и тип BOT 175
Упражнение 16.3.3 : Каков минимальный тип выражения if true then false else {}? Хоро-
шо ли это?
Упражнение 16.3.4 : Легко ли расширить алгоритмы для вычисления типов-объединений и
типов-пересечений на императивный язык со ссылками, как описано в §15.5.4 (на стр. 156)? А если
принять подход к ссылкам из §15.5.6 (стр. 157), где мы разделяем инвариантный конструктор типов
Ref на ковариантный Source и контравариантный Sink?
16.4. Алгоритмическая типизация и тип Bot
Если в отношение наследования добавляется минимальный тип Bot (§15.4), требуется несколько
расширить алгоритмы для наследования и типизации. Добавляется одно (очевидное) правило в отно-
шение наследования
Bot <: T (SA-Bot)
и два несколько более сложных правила в отношение типизации:
Γ t
1
: T
1
T
1
Bot Γ t
2
: T
2
Γ t
1
t
2
: Bot
(TA-AppBot)
Γ t
1
: R
1
R
1
Bot
Γ t
1
.l
i
: Bot
(TA-ProjBot)
Правило для наследования ясно без пояснений. Интуиция, стоящая за правилами типизации, такова: в
декларативной системе мы можем применить объект типа Bot к чему угодно (при помощи включения
продвинув Bot до любого интересующего нас функционального типа), и предположить, что получается
результат любого другого типа. Подобным образом можно рассуждать и в случае с проекцией.
Упражнение 16.4.1 : Допустим, у нас в языке имеются также условные выражения. Нужно ли
добавить еще одно алгоритмическое правило для if?
Усилия, требуемые для поддержки Bot в этом языке, не слишком обременительны. Однако в §28.8 мы
увидим, что при сочетании Bot с ограниченной квантификацией возникают более серьезные сложности.
rev. 104

176 16.4. Алгоритмическая типизация и тип BOT
rev. 104
Глава 17
Реализация наследования на ML
В этой главе интерпретатор для простого типизированного лямбда-исчисления, разработанный в
Главе 10, расширяется дополнительными механизмами, необходимыми для поддержки наследования —
в частности, функцией для проверки отношения наследования.
17.1. Синтаксис
Определения типов данных для типов и термов следуют абстрактному синтаксису с Рис. 15.1 и 15.3.
type ty =
TyR ecord of ( string * ty ) list
| TyTop
| TyArr of ty * ty
type term =
| Tm Record of info * ( string * term ) list
| TmProj of info * term * strin g
| TmVar of info * int * int
| TmAbs of info * st ring * ty * term
| TmApp of info * term * term
По сравнению с чистым простым типизированным лямбда-исчислением, добавились тип TyTop, кон-
структор типов TyRecord и конструкторы термов TmRecord и TmProj. Записи и их типы представляются
простейшим способом, в виде списка полей и связанных с ними термов либо типов.
17.2. Наследование
Представление алгоритмического отношения наследования в виде псевдокода со стр. 169 прямо
переводится на OCaml:
let rec subtyp e tyS tyT =
(=) tyS tyT ||
match ( tyS , tyT ) with
( TyRe c ord ( fS ), TyRecord ( fT )) ->
List . f or_all
( fun (li , tyTi ) ->
try let tySi = List . assoc li fS in
su btype tySi tyTi
with N ot_found -> false )
fT
| (_ , TyTop ) ->
true
| ( TyArr ( tyS1 , tyS2 ), TyArr ( tyT1 , tyT2 )) ->
177

178 17.3. Типизация
( sub type tyT1 tyS1 ) && ( subtype tyS2 tyT2 )
| (_ ,_) ->
false
По сравнению с псевдокодом мы внесли в алгоритм небольшое изменение, добавив в начало проверку на
рефлексивность. (Операция (=) — обыкновенная проверка на равенство; здесь она записана в префикс-
ной нотации потому, что в некоторых других реализациях наследования равенство заменяется другой
функцией. Операция || — булевское «или» с оптимизацией: если первая ветвь дает значение «истина»,
вторая не вычисляется). Строго говоря, эта проверка не нужна. Однако в реальных компиляторах это
очень важная оптимизация. В большинстве настоящих программ наследование используется довольно
редко — то есть, в большинстве случаев, когда вызывается проверка на наследование, сравниваемые
типы на самом деле одинаковы. Более того, если типы представляются так, чтобы структурно одина-
ковые типы всегда имели физически идентичные представления — скажем, через cons с хэшированием
(Goto 1974; Appel and Gon¸calves 1993), — то эта проверка проводится одной машинной командой.
Естественно, что проверка наследования для записей требует некоторой возни со списками. Функция
List.for_all применяет предикат (свой первый аргумент) к каждому члену списка, и возвращает true,
если все эти применения дают результат true. Выражение List.assoc li fS ищет метку li в списке
полей fS и возвращает соответствующий тип tySi; если же li не встречается среди меток fS, возникает
исключение Not_found, которое мы отлавливаем и превращаем в возвращаемое значение false.
17.3. Типизация
Функция проверки типов — прямолинейное расширение функции typeof из предыдущих интерпре-
таторов. Основное изменение коснулось ветки с применением, поскольку требуется провести проверку
на наследование между типом аргумента и типом, ожидаемым функцией. Кроме того, мы добавляем
две новых ветви для построения записей и их проекции.
let rec type of ctx t =
match t with
TmR ecord ( fi , fiel ds ) ->
let fieldty s =
List . map ( fun (li , ti ) -> ( li , typeof ctx ti )) fields in
TyR ecord ( fieldty s )
| TmProj ( fi , t1 , l ) ->
( match ( typeof ctx t1 ) with
TyR ecord ( fieldty s ) ->
( try List . assoc l fi e ldtys
with N ot_found -> error fi ( " label ␣ " ^ l^"␣ not ␣ found " ))
| TyBot -> TyBot
| _ -> error fi " Expected ␣ re cord ␣ type " )
| TmVar ( fi , i ,_) -> getT y p e Fr o m C on t e xt fi ctx i
| TmAbs ( fi , x , tyT1 , t2 ) ->
let ctx ’ = ad d b i n ding ctx x ( VarBin d ( tyT1 )) in
let tyT2 = typeof ctx ’ t2 in
TyArr ( tyT1 , tyT2 )
| TmApp ( fi , t1 , t2 ) ->
let tyT1 = typeof ctx t1 in
let tyT2 = typeof ctx t2 in
( match tyT1 with
TyArr ( tyT11 , tyT12 ) ->
if subtype tyT2 tyT11 then tyT12
else err or fi " par a meter ␣ type ␣ misma tch "
| TyBot -> TyBot
| _ -> error fi " arrow ␣ type ␣ ex p ected ")
В ветвях, относящихся к записям, вводятся новые конструкции OCaml, прежде нами не виденные. В
ветви TmRecord мы вычисляем список имен полей с их типами fieldtys из списка полей с термами
fields, с помощью List.map применяя функцию
rev. 104
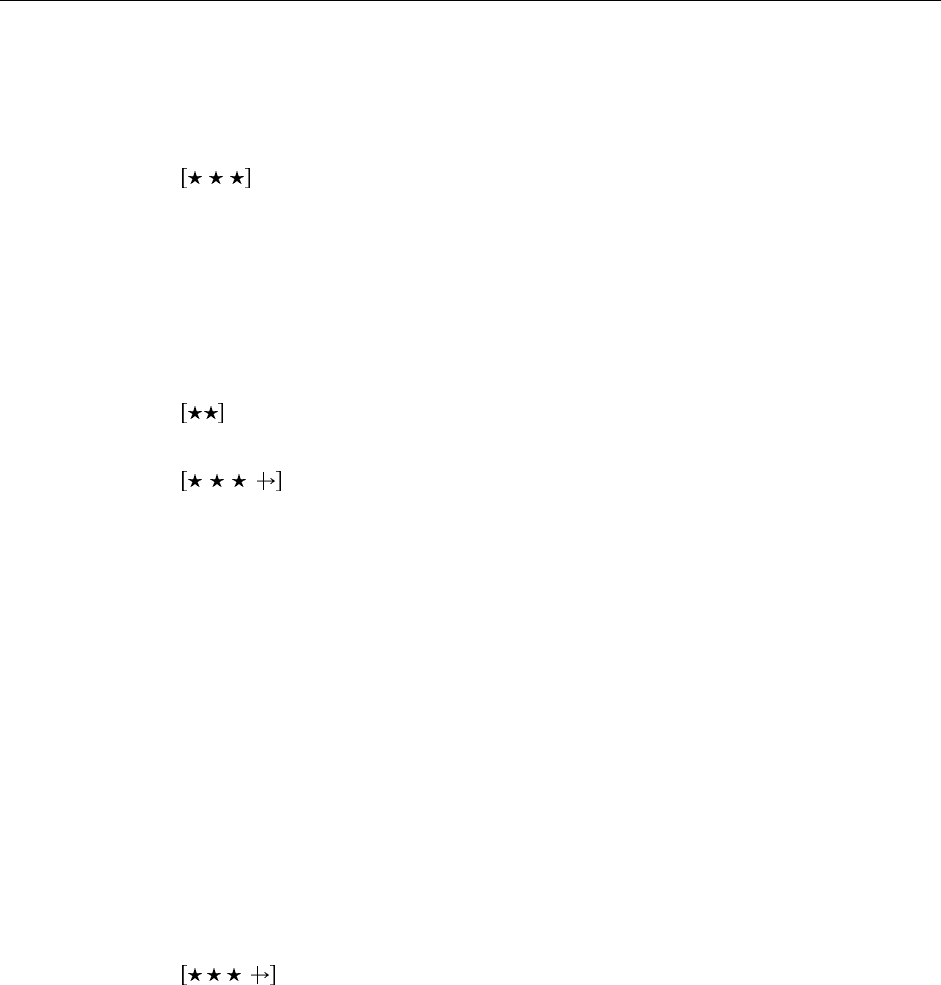
17.3. Типизация 179
fun ( li , ti ) -> ( li , typeo f ctx ti )
по очереди к каждой паре имя/терм. В ветви TmProj мы снова используем List.assoc, на этот раз
чтобы найти тип выбираемого поля. Если возникает исключение Not_found, мы порождаем наше соб-
ственное сообщение об ошибке (ˆ — конкатенация строк).
Упражнение 17.3.1 : В §16.3 показано, как при добавлении в язык с наследованием условных
выражений возникает нужда в дополнительных вспомогательных функциях для вычисления наи-
меньшей верхней грани данной пары типов. В доказательстве Утверждения 16.3.2 (см. стр. 402)
дается математическое описание требуемых алгоритмов.
Программа проверки типов joinexercise — неполная реализация простого типизированного
лямбда-исчисления с наследованием, записями и условными выражениями: даны основные функции
для синтаксического анализа и распечатки, но в функции typeof отсутствует вариант для TmIf.
Нет также функции join, от которой этот вариант зависит. Добавьте в этот интерпретатор
булевские значения и условные выражения (а также объединения и пересечения).
Упражнение 17.3.2 : Добавьте в интерпретатор rcdsub минимальный тип Bot, основываясь на
описании в §16.4.
Упражнение 17.3.3 , : Если проверка на наследование в правиле применения завершается
неудачей, печатаемое нашим интерпретатором сообщение об ошибке может быть неудобно для
пользователя. Можно его улучшить, распечатывая в составе сообщения об ошибке ожидаемый тип
параметра и реально имеющийся, но даже такую запись может быть трудно понять. Например,
если ожидается тип
{x :{} , y :{} , z :{} , a:{} , b :{} , c :{} , d :{} , e :{} , f :{} , g :{}}
а реально получен
{y :{} , z :{} , f :{} , a:{} , x :{} , i :{} , b :{} , e :{} , g :{} , c:{} , h :{}}
далеко не сразу можно сообразить, что пропущено поле d. Можно значительно улучшить диагности-
ческие сообщения, если заставить функцию subtype вместо значений true и false либо возвращать
тривиальное значение (значение () типа unit), либо порождать исключение. Поскольку исключение
порождается в том месте типа, где что-то на самом деле не складывается, можно более точно
реагировать на конкретную ошибочную ситуацию. Заметим, что это изменение не затрагивает
наблюдаемое извне поведение программы проверки: если проверка наследования возвращает false, в
этом месте процедура проверки типов все равно бы породила другое исключение (через вызов функции
error).
Перепишите функции typeof и subtype, чтобы все сообщения об ошибках были как можно более
информативны.
Упражнение 17.3.4 , : В §15.6 мы определили семантику на основе преобразования типов для
языка с записями и наследованием, используя перевод выводов типизации и наследования в термы чи-
стого простого типизированного лямбда-исчисления. Реализуйте эти преобразования, модифицируя
функцию subtype из этой главы, так, чтобы она порождала и возвращала функцию преобразования
(выраженную в виде терма), а также изменяя функцию typeof, чтобы она возвращала как тип, так
и переведенный терм. Переведенный терм тогда должен быть выполнен (вместо исходно введенного
терма), а результаты, как обычно, распечатаны.
rev. 104

180 17.3. Типизация
rev. 104
