Peube J-L. Fundamentals of fluid mechanics and transport phenomena

Подождите немного. Документ загружается.

General Properties of Flows 273

The nature of the quadratic form can be easily obtained by a geometric

interpretation. Consider the vector



321

DDD

OA . Equation [6.24] can be

written in the form:



[6.25]

This equality shows that the projection of

must be equal to OA. The

existence of the non-zero vectors

OA is possible only if cVM is greater than 1,

in other words if the flow is supersonic. We recover the result already obtained in

section 5.3.2.3. We deduce from [6.25] the value of the angle

between the normal

to the characteristic surface and the velocity direction:

MVc 1cos

The velocity thus makes the complementary angle

T

with the characteristic

surface; and so the result of section 5.3.2.3 is recovered (

M1sin

6.2.5. Elementary solutions in irrotational flows

6.2.5.1. Introduction

We will now examine some elementary solutions in simple examples of potential

equations. We will first consider the case of an incompressible fluid. The velocity

potential satisfies Laplace’s equation. Subsonic flows verifying an elliptic equation

have similar properties, but are modified by the compressibility of the fluid

([YIH 77]).

The second case studied is the acoustic wave equation, which can be obtained

via linearization and a suitable referential change in equation [6.18] and which

represents the local properties of all second order hyperbolic equations.

6.2.5.2.

Irrotational 2D plane flow of an incompressible fluid

6.2.5.2.1.

Introduction

The problem comes down to the solution of Laplace’s equation with free-slip

conditions imposed at the solid boundaries. The best adapted means for the study of

these flows involves the use of complex variables. In effect, relations [6.26] defining

the velocity potential

 and the stream function

274 Fundamentals of Fluid Mechanics and Transport Phenomena



[6.26]

are Cauchy relations between the derivatives of the real and imaginary parts,

and

, of an analytic function



zF of the complex variable

jyxz



 



[6.27]

The function



zF is the complex potential of the flow considered. Its derivative



zF ' with respect to z is the complex velocity of the expression:



jvuzF  '  [6.28]

If the function



zF is analytic, the function



zjF is also. The velocity

potential and the stream function of



zjF are, respectively,

\

and 

. The flows

associated with the two potentials



zF and



zjF are known as conjugated flows.

Any analytical function of complex variables thus provides two solutions to the

Laplace equation corresponding to two conjugated flows where the curves of

potential lines of one flow are streamlines of the other.

Consider the integral



dzzF' taken once counter-clockwise on a closed path

of the complex plane (x, y). It can be written as a function of the velocity circulation

* and of the volume flow rate

(section 4.2.1.2.2):

  

CCC

ddvdxudy

vdyudxdz

*  

³³³

 [6.29]

If the closed path C does not surround any poles of the function



zF ' , then the

function



zF is uniform: it takes on the same value after any excursion of the

variable z on the contour C. The flow across C and the circulation of the velocity on

C are zero. If C contains a pole of



zF ' , then the value of the function



increases by

jq* with each excursion around C (see an example of the vortex in

section 6.2.5.2.2).

As the velocity field is determined by the Laplace equation, the pressure is given

by Bernoulli’s second theorem [6.14].

The simplest example of an irrotational flow is a uniform velocity field

corresponding to the complex potential







where U and B are complex

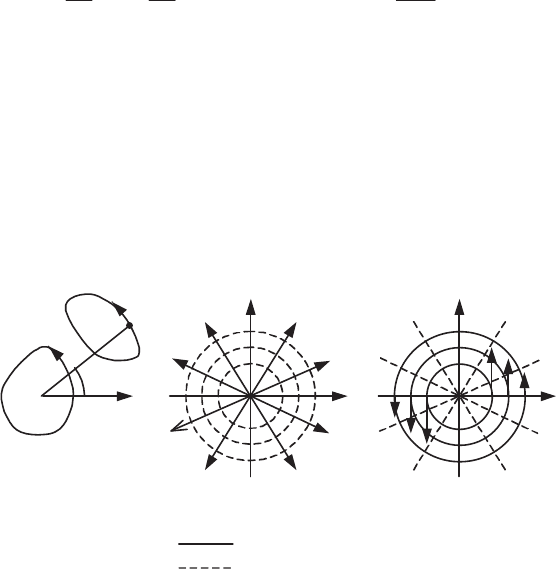
General Properties of Flows 275

constants. The velocity Cartesian components Re( ) and Im( )

uUv U





can be

immediately obtained from the complex velocity



UzF '.

NOTE

–

Time is not a variable in Laplace’s equation, but it can be a parameter

present in the boundary conditions and the coefficients of the solution. The result of

this is that initial conditions do not have any meaning for this equation.

6.2.5.2.2.

Source and vortex

A source and a vortex centered at the origin of the coordinate system are

conjugated flows corresponding to the complex potential



zF and to the complex

velocity



zF ' expressed in plane polar coordinates (with

rez ):

 

zFjr

')ln(

 [6.30]

The application of formula [6.29] to a closed contour C

(Figure 6.5a) which

does not contain the origin leads to zero volume flow rate and circulation, since after

one path counter clockwise, the variation of the polar angle

is zero. On the other

hand, if the closed contour C

(Figure 6.5a) contains the origin, the variation of the

angle

T

is equal to 2

and the integral



dzzF' is equal to j A:



jAjqdzzF

*

' [6.31]

(b) source (or sink) (c) vortex

streamlines

potential lines

T

(a)

Figure 6.5.

(a) Integral of complex velocity on a closed path,

(b) flow of a source and (c) of a vortex

276 Fundamentals of Fluid Mechanics and Transport Phenomena

When the quantity A is real, application of formula [6.31] over a closed contour

containing the origin leads to a volume flow rate Aq

, while the circulation

of the velocity is zero on all closed curves. The function



zF represents the radial

flow caused by a source (positive A) or a sink (negative A) of volume flow rate q

The potential



zF and the complex velocity



zF ' can be written:

 

zFjr

vvv

')ln(

 [6.32]

We deduce from this the velocity potential

, the stream function

and the

radial and tangential components, u

and u

, of the velocity vector:

[6.33]

The potential lines are circles centered on the origin O and the streamlines

( const)

# 

are straight lines lying on radii from the origin O (Figure 6.5b).

If the constant A is imaginary, application of formula [6.31] to a closed contour

containing the origin leads to the circulation jA

, or,

 jA . The volume

flow rate is zero across any closed surface C. The function



zF therefore

represents the flow of an irrotational point vortex centered on the origin (Figure

6.5c). The potential



zF and the complex velocity



zF ' can be written:

 

zFrjz

')ln(

 

 [6.34]

We can deduce from this the velocity potential

, the stream function

\

and the

radial and tangential components, u

and u

, of the velocity vector:

;0;ln

;

2 rr



[6.35]

The potential lines are straight radii coming from the origin and the streamlines

are circles centered on the origin.

General Properties of Flows 277

NOTES

–

1) The values of the volume flow rate and circulation can be easily found from

the components of the velocity by direct calculation; we will leave it to the reader to

verify this.

2) The vorticity

of the irrotational point vortex is zero at all points, except at

the origin where it takes on the value of a Dirac impulse, a multiplying factor

excepted. The circulation * can be alternatively written as the flux of the rotation

vector across the surface S enclosed by the curve C. The flux is only non-zero for

surfaces containing the vorticity impulse.

3) When the source, the sink or the vortex are placed at z



and not at the origin,

the variable z in the functions



zF and



zF ' is replaced by

zz  .

6.2.5.2.3.

Superposed flows

Any linear combination of harmonic functions or of analytic functions of

complex variables is also a harmonic or an analytic function. We can therefore

construct new solutions from known solutions. While the velocity fields can be

superposed, the same is not true for the pressure fields, as Bernoulli’s theorem is not

linear. Let us consider some common simple examples.

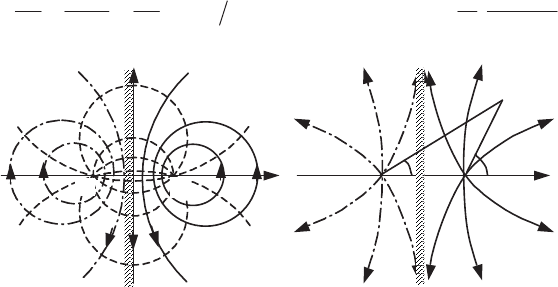
The potential and the complex velocity of the superposition of a source and a

sink with the same flow rate or of two vortices of opposite circulation positioned at

the points A and A’ of coordinates (0, ± a) (Figure 6.6a) can be obtained from

equation [6.30]:



.';'ln

zFjrr

azK









[6.36]

A' x

(a) (b)



Figure 6.6.

Flow of a vortex (a),

of a source (b)

placed near a solid wall

278 Fundamentals of Fluid Mechanics and Transport Phenomena

Similarly, the potential and complex velocity of the superposition of two

identical sources or of two vortices of the same circulation positioned at A and A’

can be written:





..';''ln

zFjrr



 

with (Figure 6.6b):









MAAxAMAxMArAMr ',';,;'';

The constant A takes on the value q

(respectively j*) for the sources or sinks

(respectively two vortices of identical or opposite circulation). The other quantities

(

and the velocity components) of these flows can also be obtained by taking the

difference or sum of the corresponding values of the base flows.

When the axis Oy is a streamline which can be “solidified” (solid boundary with

free-slip condition) we have a representation of the flow associated with a vortex or

a source in the presence of a plane wall. These interesting specific cases (Figure 6.6)

are obtained respectively with:

 two vortices of opposite circulation whose stream functions derived from

[6.35] are equal to

2 r

 and for which we obtain the axis Oy for

;

 two sources of equal flow rate whose stream function (derived from [6.33]) is:





and for which we obtain the axis Oy for



doublet

is a combination of a source and a sink of the same strength, in terms

of their absolute value, of which the distance

tends to zero such that the quantity

is equal to

(moment of the doublet). A series development in

in formula

[6.36] leads immediately to an expression for the complex potential of the doublet:

zCzF

2)(



The velocity potential

, the stream function

and the radial and tangential

components,

and

of the velocity vector can be derived:

sin1

;

cos

sin

cos



The potential lines (respectively the streamlines) are circles centered on the axis

Ox (respectively Oy) and tangent to the axis Oy (respectively Ox).

General Properties of Flows 279

6.2.5.2.4.

Flow around a circular cylinder

Consider a straight circular cylinder of radius R, of unit extent, placed in a flow

(Figure 6.7) whose velocity at infinity is equal to xU

(U is a constant or a function

of time). Let us use polar coordinates and consider the complex potential, a

superposition of a uniform flow and a doublet at the origin:

( ) with:

i

Fz U z z re

¬







 











®

[6.37]

The circulation of the velocity vector on a curve surrounding the cylinder is

zero. The velocity potential

, the stream function

and the radial u

and tangential

components of the velocity vector in polar coordinates can be derived from

[6.37]:

T\TM

sin)1(

cos)1(

sincos







We can verify that for

we have cte 0

and 0

u : the circle of

radius

R is a streamline.

Some particular values of the velocity components allow us to outline the form

of the streamlines. In particular, on the circle

, we have:



sin2URu 

and on the axis Ox (

= 0 or S), u

is positive (negative) for r > R ( R

 ): there

exist two points A and A’ of zero velocity stagnation points, (section 6.2.5.2.5) of

the flow on the cylinder (Figure 6.7a).

When

z tends to infinity, F (z) tends to U

z, the complex potential of a uniform

flow. The velocity field presents a symmetry with respect to the axes Ox and Oy

(between upstream and downstream).

We obtain an

irrotational flow with circulation * around the cylinder of radius R

by superposing the preceding flow and a point vortex, whose streamlines are circles

centered on the origin. The complex potential and the complex velocity of this flow

are:

UzFz

zUzF

)1()(';ln

)()(



 [6.38]

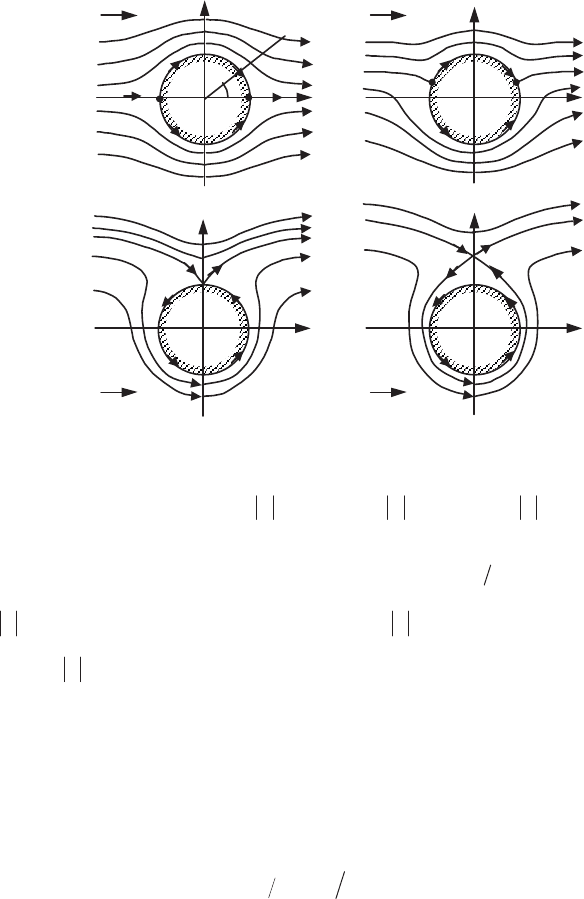
280 Fundamentals of Fluid Mechanics and Transport Phenomena

A'O

T

A'O

(a) (b)

Figure 6.7.

Flow of an inviscid fluid around a circle:

0; 4; 4; 4RU RU RU** * *  (a) circulation (b) (c) (d)



The expression for the velocity



RURu

2sin2 * on the circle of

radius R indicates that two stagnation points A and A’ are found on the circle if

4* (Figure 6.7b). These are joined for RU

4 * (Figure 6.7c).

For

4!*

, the points of zero velocity are the solutions of the equation



0' zF ; letting

yjz , we find for y

two roots, only one of which is external

to the circle of radius R (Figure 6.7d).

Bernoulli’s second theorem allows us to calculate the pressure p

on the cylinder

from the velocity distribution on this one. We here limit ourselves to the case of a

steady flow, as unsteadiness introduces secondary effects due to the added mass

([YIH 77]). We have:



constant22sin2

* RUp

STU

[6.39]

The force

exerted by the fluid on the cylinder (per unit extent) can be

decomposed into the drag D and the lift L (

yPxTF



). These can be calculated

from expression [6.39] for the pressure. We find immediately:

General Properties of Flows 281

³³

*  

UTTTT

.sin;0.cos URdpLRdpD

Regardless of the form of the obstacle, these results are true for the drag

(d’Alembert’s paradox) and for the lift (Kutta-Joukowski theorem [YIH 77], [PAR

98]).

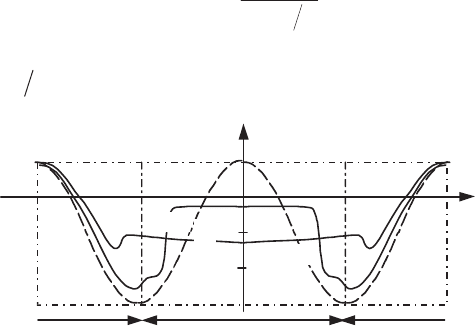
Comparisons with experiment

In the case where * = 0, this theoretical pressure distribution on the cylinder

(Figure 6.8, curve a) can be compared with experimental results. In Figure 6.8, we

have shown pressure variations





(difference between the wall

pressure p and the pressure

p in the uniform flow normalized by the dynamic

pressure

) as a function of the angle T (defined in Figure 6.7a).

SS S

–

S T

-3

-2

-1

downstream face

upstream faceupstream face

Figure 6.8.

Distribution of the pressure coefficient on a circular cylinder

(

= 0):

(a)

irrotational

flow

;

(b) laminar separation

;

(c)

turbulent separation



The values of the preceding calculation are relatively close to those measured on

the upstream side of the cylinder, up to the angular position where a separation of

the flow from the cylinder occurs and a wake is formed (section 6.5.3.7). The

pressure measurements at locations situated on the wall where the flow has

separated illustrate a strong flow dissymmetry between the upstream and

downstream faces, which leads to a non-zero value for the drag (whence

d’Alembert’s paradox given to the “theoretical” result). The difference, which is

quite small, between the calculation and the measurement on the upstream face of

the cylinder comes from the fact that an inviscid fluid flow is not produced about the

cylinder, rather it is produced about the ensemble constituted by both the cylinder

and its wake.

282 Fundamentals of Fluid Mechanics and Transport Phenomena

The non-zero drag force D exerted by the fluid on the cylinder can be explained

by the presence of the wake on the downstream face, on which a pressure force is

exerted which is greater than that exerted on the upstream face. This force, known as

pressure drag, is obviously proportional to the dynamic pressure

. The value

of the separation angle D (and therefore of the drag) is different ([SCH 99], [YIH

77]), depending on where the boundary layer (section 6.5.3) is laminar (subcritical

flow, Figure 6.8, curve b) or has become turbulent (supercritical flow, Figure 6.8,

curve c).

The lift due to the circulation (Kutta-Joukowski theorem) is indeed observed for

wing profiles and for cylinders in rotation. However, the question as to the

mechanism by which the circulation has been created has not been discussed. The

latter is created by the beginning of the fluid movement about the airfoil as a result

of viscous stresses on the wall (see section 6.6.4.1). However, the Kutta-Joukowski

theorem is satisfied, and the effect of the lift is a curved trajectory for bodies being

in rotation (the Magnus effect); this phenomenon is used in games with balloons and

balls (the balls are “cut”).

The lift of a stationary circular cylinder can also result from actions which

generate dissymmetries of the wake by modification of viscous effects in the vicinity

of the wall (dissymmetric sucking of the boundary layer).

6.2.5.2.5.

potential flows

Consider the plane polar coordinate system (r,

) and flows whose potentials and

complex velocities are given by:



111

sincos





njnn

nnn

enKrnKzzF

nrjKnrKKzzF

The straight lines

are streamlines terminating at, or issuing from, the

zero velocity point 0 z (for negative n). The case 2 n corresponds to the usual

stagnation point of a flow (points A and A’ of Figures 6.7a, Figure 6.7b and point A

in Figure 6.7d). The case 3 n corresponds to a higher order stagnation point

(point A in Figure 6.7c). Taking viscosity into account in these flows is possible

with self-similar solutions of the boundary layer where n can take on any value

([SCH 99], [YIH 77]).

A ship with “sails”, “l’Alcyon”, has been built using this principle by Y. Cousteau and L.

Malavard.