Peube J-L. Fundamentals of fluid mechanics and transport phenomena

Подождите немного. Документ загружается.

Transport and Propagation 243

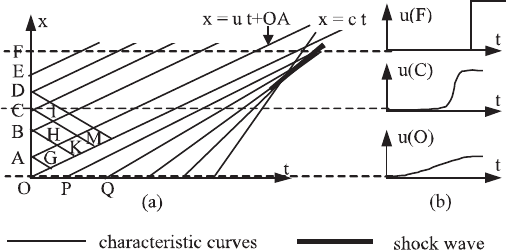
Figure 5.9.

(a) Application of the characteristics method and evolution of

the characteristic straight lines for a positive and growing variation of pressure

(or velocity); (b) evolution of the velocity t the points O, C and F

On the other hand, when the pressure and velocity variations are positive and

increasing (compression), the slope of the characteristic lines is an increasing

function of time (Figure 5.9a). They thus form a beam of straight lines which tighten

and finally intersect. This situation leads to a compression of the wave front as it

propagates, which eventually leads to a discontinuity. Indeed, we note in this last

case that it is impossible (equation [5.44]) to have more than one characteristic curve

of each family at a given point. The result of this is that a continuous solution cannot

exist everywhere in the influence domain of the boundary conditions which are

specified. A discontinuity thus appears (a shock wave) downstream of which the

calculation of the solution can only be achieved using the conditions which result

from the shock wave. Figure 5.9b shows the form of temporal variation at the origin

O, and then at points C and F.

The formation of a shock wave can be physically explained in the following

elementary manner: the increasing pressure can be decomposed into a succession of

elementary (acoustic) waves which propagate at the speed of sound. Each of these

elementary waves corresponds to an isentropic compression which increases the

temperature, and thence the speed of sound. Each elementary wave will thus travel

slightly faster than its predecessor, which it will finally catch. These waves are thus

concentrated at a point where they form a discontinuity. It is clear that when the

pressure decreases, an inverse process occurs: the elementary waves are spread out.

244 Fundamentals of Fluid Mechanics and Transport Phenomena

5.5.3. Plane steady supersonic flow

We have already studied this flow in section 5.3.2.3, and so we will limit

ourselves here to a qualitative discussion. Consider a uniform homentropic flow next

to a wall in a semi-infinite medium (Figure 5.10).

Figure 5.10.

Plane supersonic flow around (a) a convex wall

and (b) a concave wall

Bernoulli’s first theorem is valid everywhere in the flow, as are the Saint-Venant

and Hugoniot relations (section 4.3.2.3). The characteristic curves form an angle

with the streamlines, defined by

M1sin r

If the wall is convex (Figure 5.10a), the streamlines spread and the density

decreases while the velocity V

increases (supersonic expansion, section 4.3.2.3.4).

The velocity (direction and modulus) propagates from the wall along the

characteristic of a positive slope, and which is the only characteristic of consequence

here (straight line C

, C

,… … from A, B, etc.); the Mach number thus increases

and the angle D decreases in the downstream direction. Similar to the previous

example, we see divergent characteristics straight lines.

In the presence of a concave wall, an inverse situation occurs: the streamlines

tighten up, leading to a reduction in the velocity associated with a compression; the

Mach number decreases, and the characteristic lines intersect. Thus, a shock wave is

formed (Figure 5.10b).

5.5.4. Flow in a nozzle

A nozzle is a truncated conduit comprised of a convergent section followed by a

divergent section (Figure 5.11). When it separates two independent gaseous spaces,

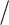
Transport and Propagation 245

it supports a flow between an upstream region at pressure p

and a downstream

region at pressure p

< p

). We will assume that viscous friction effects at the

nozzle walls are small enough to be negligible up to the exit. The flow exiting from

the nozzle is thus in the form of a jet; the main viscous dissipation corresponds to

the energy loss due to the pressure difference; this dissipation occurs in the jet

downstream of the nozzle exit. Experience shows that we can consider that the

pressure in the exit plane is equal to p

as long as the jet is subsonic.

Assuming that the quantities associated with the gas are constant in a normal

section, the Saint-Venant relation (section 4.3.2.3.3) provides an expression for the

velocity as a pressure function using the generation conditions (initial conditions at

zero velocity in the upstream domain) and in particular the velocity V

in the exit

section S

. The isentropic transformation relation (

const



) determines the

density

in the exit plane. From this we can deduce the mass flow

EEEm

SVq

in the nozzle.

However, we have shown (section 4.3.2.3.4) that a stream tube resulting from a

given set of generation conditions has a maximum flow rate

cccm

SVq

max

which occurs when the speed of sound c is attained in the smallest cross-section. We

are thus faced with the following alternative:

– either the flow rate q

evaluated at the exit plane is less than or equal to q

m max

and we can calculate the continuous flow in the nozzle;

– or the flow rate q

evaluated at the exit plane is greater than q

m max

and the

problem thus posed does not have a solution.

In the first case, the Hugoniot relation [4.39] in its differential form (section

4.3.2.3.4) shows that the velocity increases in the convergent part of the nozzle up to

a value which is at most equal to the speed of sound c

at the throat, and which then

decreases such that its value at the exit plane V

is that previously predicted. The

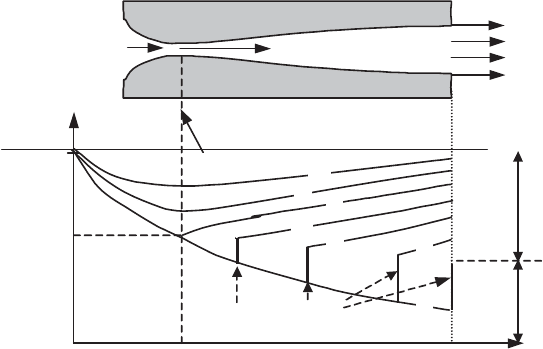
flow is then everywhere subsonic (V < c). Figure 5.11 shows the pressure variations

(contrary to the velocity variations) in the nozzle for regimes 1, 2 and 3 which are

entirely subsonic. For pressures p

and p

, the velocity at the throat V

max

is less

than the speed of sound, while for the pressure at the exit p

the throat velocity is

equal to the speed of sound c

246 Fundamentals of Fluid Mechanics and Transport Phenomena

upstrea

p = p

downstream:

p = p

nozzle throat

jet

subsonic

turbulent jet

supersonic jet

shock waves

max

or c

E sup

Figure 5.11.

Flow regimes in a nozzle

In the second case, the flow in the convergent part of the nozzle is subsonic, then

it becomes supersonic after passing through the throat where the velocity magnitude

is equal to the speed of sound c

and the critical conditions (p

and

) are attained.

However the continuous supersonic solution, calculated using the Saint-Venant

relation in the exit plane using the generation conditions, is unique. It provides the

value p

Esup

for the exit pressure, which is not equal to the exit pressure imposed p

However, the supersonic flow in the nozzle must match the exit conditions. This

adaptation is achieved by means of a shock wave. So long as the shock wave

remains within the nozzle, it is plane (from p

to p

in Figure 5.11). For lower

pressures (p

E sup

< p

) we have a more or less complex system of shock

waves in the jet (under-expanded jet). For p

less that p

E sup

, the adaptation is

achieved by means of expansion waves (over-expanded jet).

The idea of characteristic curves and of propagation do not hold for the

differential equation of the 1D model nozzle. We note only the non-existence of a

continuous solution which verifies the boundary conditions at the exit. In fact, the

flow in the nozzle is governed by the models outlined in section 5.3.2.3:

– for the subsonic part of the flow, the system of partial differential equations is

elliptic and the flow is determined by the boundary conditions on all boundaries. Its

solution assumes Neumann conditions which are here known in the upstream region,

Transport and Propagation 247

on the walls and in the exit section of the subsonic flow: depending on the regime,

this is either at the nozzle exit or at the throat;

– from the throat of nozzle in the sonic regime, and up to the shock, the subsonic

flow is governed by the 2D plane mode discussed in section 5.3.2.3, the fluid being

assumed to be isentropic. The supersonic zone of flow belongs to the influence

domain of the “upstream” conditions (section 5.4.5.3) which are here situated at the

sonic throat. An exit condition cannot influence the supersonic flow, as the

information cannot move upstream due to the characteristic curves which all have

slopes

212

)1(



r M . In these conditions no continuous supersonic solution can

account for the conditions at the exit.

The specific characteristics of the plane 2D supersonic model also generally

correspond to the 1D model whose behavior is appropriate but without explaining

the difficulties: we observe that data given at two conditions, one at the throat and

the other at the exit, leads to an impossibility because of the existence of a singular

point for M = 1 in [4.38] and [4.39]. Such difficulties are often encountered in fluid

mechanics, where a global model can lead to contradictions (or to “paradoxes”) that

only a more refined model can explain.

The shock wave is a boundary between two spaces which cannot communicate

completely, the upstream space not being able to receive information regarding the

pressure at the exit. However, matter crosses the shock wave and the balance

equations for the extensive quantities must be satisfied through the shock.

In conclusion, a continuous solution of the 1D equations does not usually exist in

isentropic compressible fluid, for a nozzle whose throat velocity is sonic (critical

velocity). From a physical point of view, we could also consider that the shock wave

comprises an accumulation of pressure waves which travel from the downstream

and which stop when they can no longer do so.

The shock wave is a dissipative structure which leads to an increase in entropy

([LAN 89], [YIH 77]), viscosity playing an important role at the scale of the mean

free molecular path, for which a continuous viscous model is appropriate for the

shock wave.

Let us finish by highlighting a particularly useful application for nozzles

operating in the supersonic regime whose mass flow is fixed and depends only on

the upstream conditions. Such a nozzle, placed upstream of an installation, perfectly

regulates the flow if the upstream generation conditions are fixed, which is often the

case in laboratory situations: downstream perturbations can have no influence on the

mass flow of the device. The pressure loss of such a nozzle is relatively small (| 10

pascal).

248 Fundamentals of Fluid Mechanics and Transport Phenomena

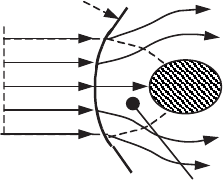
5.5.5. Separated shock wave

A problem of the same kind is posed by a supersonic flow around an obstacle

which imposes boundary conditions which cannot travel upstream in the supersonic

flow. In particular, upstream of the obstacle there exists the stagnation point A,

where the velocity is zero, and therefore a subsonic zone of flow in the region near

the surface.

shock wave

supersonic zone subsonic zone

Figure 5.12.

Detached shock wave in front of a body in a supersonic flow

Similar to the case of the nozzle, the adaptation of the supersonic flow to

downstream conditions occurs by means of the shock wave.

5.5.6. Other discontinuity categories

Combustion phenomena in gaseous flows obey the fluid dynamics equations

which we have already discussed in Chapter 4. We must however introduce the

properties of chemical reactions using the methods of chemical thermodynamics

which must be applied to the moving matter. Without containing new physical

phenomena, the formalism obtained combines the difficulties of the two domains.

We cannot address these questions in detail in this book (see [BOR 00], [KIR 67],

[OPP 06], [WIL 65], [WIL 85]). Schematically, the possibility of a chemical

reaction amounts to the introduction of a heat source associated with a local increase

in temperature: we thus notice that a shock wave can trigger a chemical reaction

which can augment its effects considerably, transforming the shock wave into a

detonation wave.

Other domains of fluid mechanics also involve hyperbolic equations. Such is the

case for flows including a free surface (see section 6.2.6) in which we observe the

propagation of surface waves (swell in the sea) and flows of stratified fluids (vertical

distribution of density) which present similar properties. We encounter analogous

Transport and Propagation 249

phenomena to those discussed for a gas, and in particular the possibility of

discontinuities called hydraulic jumps [YIH 77] or tidal bores in estuaries which

propagates against flowing water.

5.5.7. Balance equations across a discontinuity

A velocity discontinuity undergone by a material body in movement assumes

infinite external forces and (finite) inertial effects associated with non-Galilean

reference frames are therefore neglected. The equations for the shocks and collisions

can be written in any reference frame, both in particle or solid body mechanics and

in the dynamics of continuous media.

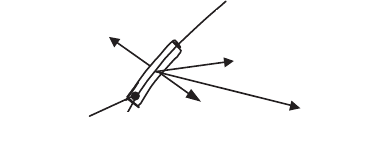
We will consider a discontinuous surface which is crossed by matter in

movement and we will designate by the indices 1 and 2 the upstream and

downstream quantities of the discontinuity. We apply the balance equations in

global form in a thin volume D comprised of two parallel surfaces at the

discontinuity S, of area ds and with normals oriented towards the exterior (Figure

5.13). The indices n and t designate the velocity components normal and tangent to

the surface of the discontinuity.

1 2

1

2



Figure 5.13.

Balance on a discontinuity surface (shock)

We now write the balance equations for the extensive quantities in global form

(section 4.5) in the domain D for the following quantities:

– mass (section 4.5.2):

2211

U U [5.53]

– momentum (section 4.5.4):

ntnt

VVVV

VpVp

222111

222

111

U U

U U

[5.54]

250 Fundamentals of Fluid Mechanics and Transport Phenomena

– total energy (enthalpic form) (section 4.5.6):

U

222

111

[5.55]

– chemical species (i =1,2 …):

niinii

2211

[5.56]

We can immediately deduce the continuity of the tangential velocity components

across the shock:

[5.57]

NOTE

–

In the presence of a chemical reaction on the surface S (detonation or

deflagration wave), balances [5.55] and [5.56] take the following form:

niiminiir

VQV

2211

 

[5.58]

where, Q

and Q

denote the mass of species i and thermal surface power released

by the chemical reaction for the mass flux

crossing the shock S, the

enthalpies h

being taken as equal to C

for perfect gases (“sensible enthalpy”).

5.6. Some comments on methods of numerical solution

5.6.1. Characteristic curves and numerical discretization schemes

The numerical resolution of a system of first order differential equations with

initial conditions (Cauchy) given at a point can be achieved from place to place: by

discretizing the first derivatives, we calculate the value of the unknown vector

function at a point using the values at the previous point. However, we often have

conditions on either extremity of an interval instead of Cauchy conditions, in

particular when the system is associated with a flow between solid boundaries. We

therefore often use a shooting method: the missing initial values are determined by

successive approximations so as to obtain suitable values at the other extremity of

the interval.

Such an iterative procedure presents the advantage of not involving the inversion

of a large matrix.

Transport and Propagation 251

A numerical solution consists of replacing equations of a differential kind with

finite difference algebraic equations obtained by means of a discretization of the

derivatives which can be performed in many different ways which we will quickly

evoke further. By way of a simple example, consider the transport equation in which

the velocity u is constant:



[5.59]

The axes Ox and Ot are discretized with step-sizes

x and

t such that 'x = u.'t.

We will here approximate the derivatives by formulae using the values at two points.

We calculate the partial temporal derivative using the formula:

  



nnnnnn

txftxf

[5.60]

We approximate the spatial derivative

at the point x

by its value at the

instant t

n-1





such that we have a simple, explicit scheme for the

discussion. Take as an approximation of





one of the following

schemes, which are apparently locally equivalent:

– upwind scheme:

  

1111





nnnnnn

txftxf

;

– downwind scheme:

 

1111





nnnnnn

txftxf

;

– centered scheme:

 

11111





nnnnnn

txftxf

Substituting these expressions into [5.59] we can calculate the value of the

function



txf , as a function of its values at the instant t

n-1

at the points next to

the axis Ox. We obtain for the different schemes:

– upwind scheme:

 



nnnn

txftxf ;

– downwind scheme:

  

111

,,2,





nnnnnn

txftxftxf ;

252 Fundamentals of Fluid Mechanics and Transport Phenomena

– centered scheme:

 

11111





nnnnnnnn

txftxftxftxf

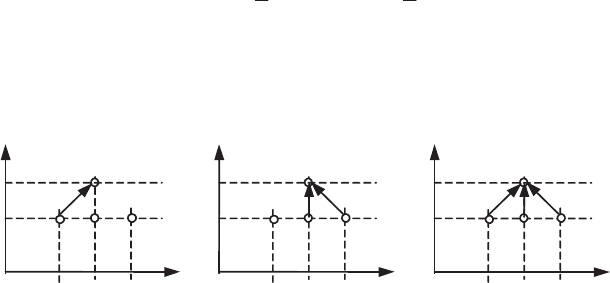
Figure 5.14 schematically shows the transmission of numerical information

between the points of the discretized network for the three numerical schemes.

n+1

n-1

n+1

n-1

n+1

n-1

(c): centered scheme

(

)

: downwind scheme (a): upwind scheme

Figure 5.14.

Transmission of information in the numerical resolution

following different discretization schemes

Now, equation [5.59] is hyperbolic and its characteristics are the straight lines

,xut const

which are trajectories of the uniform velocity field u. To simplify

matters, the discretization ('x = u.'t) was chosen such that these straight

characteristics pass through the points of the computation. Let us examine a

particular case of the problem, defined by the boundary conditions which

corresponds to transport at velocity u of a unit step function from the origin in a field

with zero initial values:

0, 0: ( ,0) 0

0, 0: (0, ) 1

txfx

txft

 

p 

[5.61]

Table 5.1 indicates, on each line, the numerical values obtained by means of the

three numerical schemes for the six points on the axis Ox at the six first instants (0,

't, 2't, 3't, etc. from the bottom of the table).