Peube J-L. Fundamentals of fluid mechanics and transport phenomena
Подождите немного. Документ загружается.

General Properties of Flows 263
For
an inviscid fluid which is homentropic or with constant specific mass, the
preceding equations are simplified:
°
°
¯
°
°
®
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
ZH
U
Z
UZ
Z
Z
Z
G
G
G
G
G
G
G
.
0
dt
d
Vdiv
t
Vrot
t
[6.7]
6.1.2.2.
Interactions between vorticity and strain rates
We will characterize the effects of the volume source term
ZH
G
. (
ijj
H
Z
.
) which
translates an interaction between vorticity and the strain-rate tensor. In order to
simplify matters let us consider equation [6.7] for a constant specific mass:
. ... or: . ...
i
ij j
d$
d$
%$ % $
dt dt
G
G
Let us first of all examine the effect of the first component
1
Z
of the rotation
vector on itself. The corresponding equation can be written:
1
1. 11
...
d$
$%
dt
This demonstrates the creation of
1
Z
if the source term
111
.
H
Z
is positive, for
example if
1
Z
and
11
H
are positive; thus,
11
H
is the rate of increase of the
component u
1
of the velocity in the x
1
direction (section 3.3.4), and it leads to a
stretching of the matter along this axis: a stretching of the matter along a given
direction increases the corresponding component of the rotation vector (Figure
6.2a). This result is in fact analogous to the intensity conservation of a vortex tube,
the stretching rate being inversely proportional to the variation velocity of the tube
cross-section.
Now consider the source term
211
H
Z
in the equation for the component
Z
2
:
2
1. 21
...
d$
$%
dt
The strain-rate
21
H
amounts to a shearing of the type
2
1
x
u
w
w
(section 3.3.4). We
therefore see here the creation of the component
2
Z
, along the axis Ox
2
, by the
264 Fundamentals of Fluid Mechanics and Transport Phenomena
component
1
Z
(Figure 6.2b), in other words a tilting of the rotation vector (a
gyroscopic effect).
x
1
Z
1
Z
1
(a)
x
2
(b)
x
1
u
1
Z
1
Z
2
Z
u
1
u
1
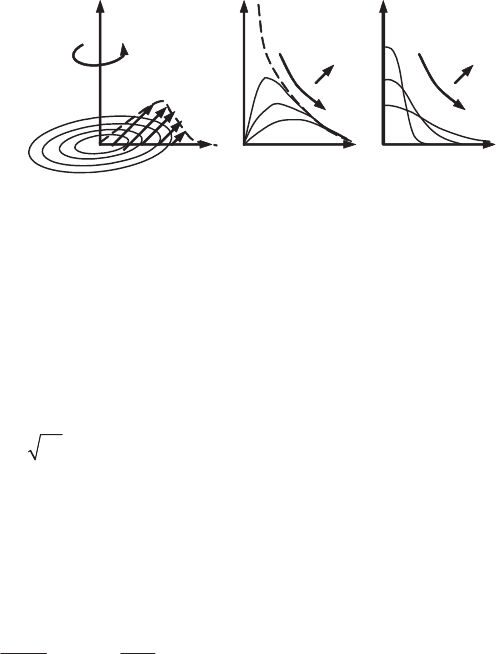
Figure 6.2. Deformation of a vortex: (a) stretching in a lengthening velocity;
(b)
tilting in a shear velocity
These properties are true for the three spatial directions; their effect is the
creation and maintenance of the 3D character of rotational flows.
If the fluid is compressible, the second term of material derivative [6.3] contains
the term
Vdiv
G
G
.
Z
which translates a reduction of
Z
G
proportional to the
expansion
,
G
divV
leaving the angular velocity constant in a
material volume. This
term is contained in the first term of vorticity equation [6.5] written with the mass
quantity
U
Z
G
.
6.1.2.3.
The 2D plane flow
The vorticity source term
ijj
HZ
.
presents a marked 3D character but disappears
in a 2D plane flow, because the rotation vector has only a component
Z
perpendicular to the velocity plane, and so we have:
0.0
0
000
0
0
.
2221
1211
¸
¸
¸
¹
·
¨
¨
¨
©
§
¸
¸
¸
¹
·
¨
¨
¨
©
§
Z
HH
HH
HZ
ijj
In the 2D case, the rotation vector (or the vortex) satisfies the scalar equation:
ZQ
Z
'
td
d
[6.8]

General Properties of Flows 265
In a 2D plane flow,
the vorticity equation is a convection-diffusion equation
which ensures the conservation of the rotation in all space (see definitions of
diffusion terms in Chapter 2).
For an inviscid fluid, scalar equation [6.8] for the vorticity is an equation
describing the transport of vorticity by the matter:
0
dt
d
Z
[6.9]
6.1.2.4.
Diffusion of the vorticity in a viscous fluid
By way of an example, consider equation [6.8] of an incompressible Newtonian
fluid in plane two-dimensional flow. It has the form of a heat convection equation
(section 4.3.4.1.6) or of the equation for the diffusion of chemical species (in weak
concentration) with source terms and diffusion terms: vorticity is diffused by viscous
action.
Let us examine the case of a vortex system of revolution about the axis Oz and
whose velocity field, parallel to the plane Oxy and of zero radial component, has a
tangential component equal to
(
)
t
r
V
,
T
. The vortex vector field
tr,
Z
, parallel to
Oz, is a function of r and t. Equation [6.8] can be written:
Z
Q
Z
'
w
w
t
[6.10]
or, in plane polar coordinates:
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
r
r
rrt
ZQZ
[6.11]
The reader can easily verify that equation [6.11] has a class of solutions
2
in the
form
K
ft
n
where we have introduced the new variable tr
QK
4
2
. The
function
K
f satisfies a differential equation which depends on the parameter
n.
The circulation
tr,* of the velocity vector along the circle centered on the
origin and of radius r is equal to the flux of the vector 2
Z
across this circle:
2
These solutions are “self-similar” like solution [5.52] (see footnote 5 in section 5.4.5.4).

266 Fundamentals of Fluid Mechanics and Transport Phenomena
dvvftdvvftrdr
t
u
fttr
n
tr
n
r
n
³³³
¸
¸
¹
·
¨
¨
©
§
*
KQ
QSQSS
Q
0
1
4
0
1
0
2
882
4
2,
2
Suppose that after the initial instant t = 0, there is no source of vorticity
anywhere in space; the circulation on the circle whose radius tends to infinity
remains constant, and this leads to the choice 1 n . Substituting this expression
for
Z
into [6.11] we obtain the differential equation satisfied by the function
K
f :
0''' ff
K
K
A first integration gives:
const
'
ff
Integrating a second time, taking the constant of integration to be zero such that
the circulation remains constant for infinite
K
, the vorticity tending therefore to zero.
This immediately gives the desired solution:
const A
4
exp exp ,
2
¹
·
¨
¨
©
§
t
r
t
A
t
A
tr
Q
K
Z
The circulation
tr,* of the velocity vector along a circle of radius r can be
expressed as:
»
»
¼
º
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
*
t
r
Atr
Q
QS
4
exp18,
2
Its value is constant and equal to
Q
S
A8
for sufficiently large r. The velocity
V
T
(r,t) can be calculated from the circulation:
»
»
¼
º
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
*
t
r
r
A
r
tr
trV
Q
Q
S
T
4
exp1
4
2
),(
),(
2
This solution represents the diffusive spreading of a Dirac impulse of vorticity
placed at the origin (Figure 6.3). The velocity distribution decays as 1/r outside the
viscous zone (section 6.1.1.4) which contains the vorticity. The velocity gradient
General Properties of Flows 267
diminishes under the effect of viscosity which has no further real effect for a radius
a little greater than that at which the maximum is located.
r
Z
V
G
r
V
t
r
Z
t
(a) (b) (c)
Figure 6.3.
(a) Vorticity zone, (b) diffusion of the velocity and (c) of the vorticity
For a fixed radius r, when t increases, the circulation and the velocity decay so as
to tend to zero as time tends to infinity: the rotation initially concentrated on the axis
diffuses over time across the entire fluid under the action of viscosity. Defining the
radius
tR
v
of the viscous core using the condition that this contains 99% of the
circulation of the velocity vector (exp( ) = 0.01Ș
or
K
= 4.605), we have:
4.29
v
R t
.
6.1.2.5.
Lagrange’s theorem
Consider an inviscid fluid whose entropy is uniform if it is compressible. Taking
account of vorticity equation [6.8], material derivative [6.2] of the circulation of the
velocity on a closed curve C enclosing the surface S can be written:
³
¸
¸
¹
·
¨
¨
©
§
w
w
*
S
C
dsnVtor
ttd
d
0.2
G
G
G
G
G
Z
Z
Lagrange’s theorem: the circulation of the velocity vector on a material curve,
or the flux of a vorticity vector across a material surface, is conserved during
movement. In particular, if the flux of the vorticity vector across a material surface S
is zero at an instant t, it will remain zero thereafter.
As we are dealing with a material derivative, the surface S is constituted of fluid
particles. It should not contain any singularity leading to the creation of vorticity (for
example, a vortex whose intensity varies with time). We can deduce the following
very important consequences:
268 Fundamentals of Fluid Mechanics and Transport Phenomena
– if, at a given instant, the flux
S
M
is zero in a domain D of a flow regardless of
the surface S, the flow is irrotational in the domain D (it suffices to take three
elementary orthogonal surfaces to verify that the vector
Z
G
is necessarily zero).
From Lagrange’s theorem we thus see that the flow remains irrotational afterwards
in the material domain D. This situation is encountered when a flow issues from a
fluid region at rest or of uniform velocity;
– a vortex surface (or rotation surface) is a surface to which the vorticity vector
is tangent at an instant t; it moves whilst remaining a vortex surface (the flux of the
vortex remains zero on all elementary surface of rotation). In particular, a vortex
tube remains a vortex tube during any displacement of the matter of which it is
constituted. Considering the circulation of the velocity along a curve situated on the
tube and which encircles it once, we see that the intensity of a vortex tube remains
constant during its displacement: the vortex tube transports its circulation; this can
be easily seen in a rotational smoke ring (a closed rotation tube) in which smoke
makes the motion of the matter and its rotation visible;
– a vortex line (or rotation line) at instant t can be considered as an intersection
of two vortex surfaces: it therefore remains a vortex line. This results in vortex lines
being displaced with the matter.
NOTES
–
1) The notion of circulation on a closed material curve C is essential: in effect, it
deforms during its displacement with the matter. It can eventually be divided into
two curves C
1
and C
2
when passing an obstacle (Figure 6.4), but it cannot be
transformed into a third curve C
3
(Figure 6.4). The sum of the circulations
12
ī and ī
CC
over the curves C
1
and C
2
is equal to the circulation
C
* over the
curve C, whereas the circulation
3
C
* over the curve C
3
can take on any other value.
We will use an elementary example (section 6.2.5.2.2) for which the circulations
12
īī and ī
C, C C
are zero, whereas
3C
* is non-zero. This property is related to the
structure of the surface S interior to
3
C which is not simply connected (to put it
simply, it contains a “hole”) and the vector field is not continuously differentiable on
the interior of
3
C .
2) Lagrange’s theorem does not express the transport of the vorticity vector by
the matter; it only expresses a more global property. For the reasons given above, we
say that the vector field
Z
G
which satisfies equation [6.7] is “frozen in the moving
medium”.

General Properties of Flows 269
C
C
2
C
1
C
3
P
Figure 6.4.
Evolution of closed material curves in the flow around an obstacle
3) The reader will note that once again we recover here a property of flow-
information transfer over characteristic curves associated with convection.
6.2. Potential flows
6.2.1. Introduction
Lagrange’s theorem expresses the property of transport of circulation of the
velocity over any curve C in the flow of an inviscid, homentropic fluid if the fluid is
compressible. When the circulation is zero, we can perform a partial integration of
the equations of fluid mechanics over the family of characteristic curves constituted
by the trajectories: the flow is therefore irrotational and the velocity field derives
from a potential:
M
M
gradV
x
u
i
i
w
w
G
:or [6.12]
6.2.2. Bernoulli’s second theorem
Dynamic equation [4.19] can be written in the form:
0
2
2
¸
¸
¹
·
¨
¨
©
§
w
w
hU
V
grad
t
V
G
with: h the specific enthalpy (for a perfect gas:
TCh
p
) and U the potential of the
gravitational forces ( gzU
, height z being taken on a vertically ascending axis).
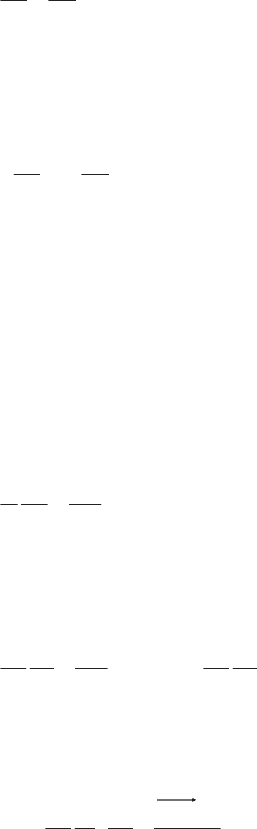
270 Fundamentals of Fluid Mechanics and Transport Phenomena
The existence of a velocity potential
M
allows the immediate integration of the
above equation with respect to the space variables, giving Bernoulli’s second
theorem:
2
const
2
! V
gz h
t
s
s
[6.13]
We note that equation [6.13] is valid everywhere in the domain of study and for
an unsteady flow, contrary to Bernoulli’s first theorem, which can only be applied in
a steady flow over a streamline. For an incompressible fluid, it can be written:
2
const
2
! V
gz p
t
¬
s
s
®
[6.14]
6.2.3. Flow of compressible inviscid fluid
The partial differential equation satisfied by the velocity potential
M
is a quasi-
linear second order equation and is derived from the Euler equations. As integration
has already been performed on the trajectories, the equation has only two families of
real or imaginary characteristic curves or surfaces which we have already seen
(section 5.4.2).
The mass conservation equation in the form [4.7] can be written:
0
1
w
w
i
i
x
u
dt
d
U
U
[6.15]
For a divariant fluid in homentropic flow, we have
U
dcdp
2
and dhdp
U
.
Replacing
U
d
as a function of dh in equation [6.15] gives:
¸
¸
¹
·
¨
¨
©
§
w
w
0
1
0
1
22
Vdiv
dt
dh
c
x
u
dt
dh
c
i
i
G
[6.16]
The potential equation can therefore be obtained by replacing the enthalpy h in
equation [6.16] by its expression as obtained from equation [6.13]:
0
2
1
2
2
¹
·
¨
¨
¨
©
§
w
w
'
M
gz
g
rad
tdt
d
c
M
M
[6.17]

General Properties of Flows 271
For the flow of a compressible fluid, we can in general neglect the gravitational
term and potential equation [6.17] becomes:
0
2
1
2
2
¹
·
¨
¨
¨
©
§
w
w
'
M
M
M
g
rad
tdt
d
c
[6.18]
or, by developing:
0
1
2
1
22
2
2
2
2
2
ww
w
ww
w
w
w
w
w
¹
·
¨
¨
©
§
w
w
ww
w
w
w
ii
j
i
j
i
j
j
x
x
x
x
x
x
c
x
x
t
tc
M
M
M
M
M
M
M
[6.19]
where, by introducing the usual notation for the velocity components
wvu ,, along
the axes
zyx ,,:
0222
1
2
22111
22222
222
2
2
2
2
2
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
tztytxttzx
yzxyzzyyxx
c
w
c
v
c
u
cc
wu
c
vw
c
uv
c
w
c
v
c
u
MMMMM
MMMMM
[6.20]
The potential equation for the flow of an incompressible fluid which can be
obtained by letting the velocity sound tend to infinity in [6.17] reduces to Laplace’s
equation:
0
2
'
ww
w
M
M
ii
x
x
[6.21]
6.2.4. Nature of equations in inviscid flows
Equation [6.19] or [6.20] is of the type studied in section 5.4. Writing explicitly
the velocity components
ii
x
u
ww
M
and the Mach number cVM , equation
[6.19] can be written:
02
1
2
2
2
2
2
2
'
ww
w
¸
¸
¹
·
¨
¨
©
§
ww
w
w
w
M
MMM
ji
ji
j
j
xx
c
uu
xt
u
tc
272 Fundamentals of Fluid Mechanics and Transport Phenomena
The characteristic directions are given by equation [5.37] which corresponds to
the preceding equation. Letting
ii
xww
1
[
D
and t
t
ww
1
[
D
(section 5.3.4), we
obtain:
02
1
2
2
2
iiij
ji
jtjt
c
uu
u
c
DDDDDDD
This characteristic equation can be written in the reduced form:
0
1
2
2
iijjt
u
c
DDDD
This form is hyperbolic
3
and the potential equation of a compressible fluid is in
general of hyperbolic character.
In the situation involving acoustic perturbations in a medium at rest, which is
obtained when the Mach number approaches zero in equation [6.19] or [6.20], the
wave equation is obtained:
0
1
2
2
2
w
w
'
tc
M
M
[6.22]
Considering now only steady solutions, the potential equation can be written:
0
1
2
2
2
ww
w
w
w
w
w
ww
w
j
i
j
iii
x
x
x
x
c
x
x
M
M
M
M
[6.23]
Its characteristic equation can be obtained as before:
0
2
¸
¸
¹
·
¨
¨
©
§
ii
j
j
c
u
DDD
or, writing the indices explicitly:
0
2
3
2
2
2
1
2
3
3
2
2
1
1
¸
¸
¹
·
¨
¨
©
§
DDDDDD
c
u
c
u
c
u
[6.24]
3
Letting
cu
jjtT
DDD
and
2
r
ii
DD
, the previous equation can be written
0
22
r
T
D
; it represents a cone of revolution around axis
T
O
D
in a 4D space.
