Peube J-L. Fundamentals of fluid mechanics and transport phenomena
Подождите немного. Документ загружается.


General Properties of Flows 283
6.2.5.3.
The wave equation
While the use of characteristics allows in principle the solution step by step of
the acoustic wave equation, writing a complete solution in this way is generally
difficult. We can immediately verify that a progressive plane wave is an elementary
solution of [6.22]:
ctnxfctnOMftx
iii
.,
M
[6.40]
(n
i
: direction cosines of the unit vector n
G
normal to the plane wave (
1 n
G
)).
The velocity and the pressure fluctuation p' can be found from solution [6.40]
and from a linearized version of Bernoulli’s second theorem [6.13]:
cVctnxcf
t
pfuuVctnxfnu
iiiiiiii
UU
M
U
w
w
'';';'
Taking the axis OX parallel to the normal
n
G
, the quantity
ii
nx of the problem of
the function f is equal to X, and the function f can be written
ctXftx
i
,
M
.
This form reveals the transmission without signal deformation (velocity potential,
velocity or pressure). We note that if
ctXf is a solution of [6.40], the same is
true of
ctXg which propagates in the opposite direction.
The superposition of certain waves can eventually lead to the disappearance of
the propagative character, and we obtain stationary waves in which all points in
space are in phase, as shown by the following simple example:
kXtkXtkXt coscos2coscos
Z
Z
Z
Conversely, any suitable superposition of harmonic stationary waves can lead to
one progressive harmonic wave:
The ensemble of progressive plane waves is thus equivalent to the ensemble of
stationary plane waves.
The equation for spherical waves
tr,
M
can be immediately obtained (the
expression for the divergence can be obtained by applying Ostrogradski’s theorem
between two spheres of radius r and r + dr). It is written:

284 Fundamentals of Fluid Mechanics and Transport Phenomena
0
111
2
2
22
2
2
2
2
¹
·
¨
¨
©
§
w
w
w
w
w
w
'
t
r
cr
r
r
tc
M
M
M
M
[6.41]
Its solution is analogous to that of the plane wave equation:
ctr
g
r
ctr
f
r
tr
11
,
M
In the case where 0{g , the expressions for the pressure and the velocity are:
ctr
f
r
ctr
f
rr
uctr
f
r
c
t
p
w
w
w
w
2
1
'
1
;'
M
U
M
U
The expression for the velocity of spherical waves differs from the expression
for plane waves by the term
ctrf
r
2
1
, which dominates in the vicinity of the
origin 0 r (nearfield term). We have, for the volume flow rate q
v
:
>@
ctr
f
ctrrf
r
rtrq
v
w
w
'44,
2
S
M
S
We see that the flow rate at the origin
tQ is equal to
ctftqtQ
v
S
4,0.
The velocity potential
M
and the pressure p can be thus be written:
¹
·
¨
¨
©
§
¹
·
¨
¨
©
§
c
r
tQ
r
p
c
r
tQ
r
'
4
U
c
;
4
1
S
S
M
6.2.6. Surface waves in shallow water
6.2.6.1.
2D equation for potential
We will now consider a problem governed by an elliptic partial differential
equation in space
zyx ,, , but whose boundary conditions induce propagative
phenomena in the plane
yx,.
Consider a horizontal plane Oxy, on which a layer of liquid is subjected to a
vertical gravitational action. Let
yx,
]
]
be the height of the free surface of the
General Properties of Flows 285
liquid. If the movement of the liquid is considered irrotational, the velocity potential
t
z
y
x
,,,
M
satisfies Bernoulli’s equation:
const
g
z
p
V
t
w
w
U
M
2
2
[6.42]
z
w
v
u
x
y
]
Figure 6.9.
Flow with free surface in shallow water
As the liquid is inviscid, the velocity is horizontal at the bottom z = 0 where w is
zero (slip condition). We will consider the case of shallow water: the flow is locally
uniform (the horizontal components u and v are independent of z), and the thickness
e is small compared with the horizontal distance L characteristic of variations of the
velocity .
G
V The volume conservation equation:
0
w
w
w
w
w
w
z
w
v
v
x
u
[6.43]
allows the magnitude of the w component to be determined: the first two terms being
of order V/L, we obtain
LVew | . The vertical component of the velocity w is of
second order with respect to the velocity .
G
V The component w can be calculated by
integration following z of equation [6.43]:
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
v
v
x
u
zw [6.44]
The velocity potential
M
is thus the sum of two terms:
– a function
I
(x,y,t) whose gradient comprises the u and v components of the
velocity;
286 Fundamentals of Fluid Mechanics and Transport Phenomena
– a small term of order
'
2
2
z
I
associated with the w component which can be
written using [6.44] by expressing u and v as a function of
I
:
'
I
z
w
[6.45]
The free surface is a material surface; its vertical velocity
]
z
w
is the material
derivative of the height
]
of the fluid particle being on this surface (kinematic
condition):
y
v
x
u
tdt
d
w
z
w
w
w
w
w
w
]]]]
]
Substituting into [6.45] gives:
M
]
]
'
dt
d
[6.46]
As this
w
component is small compared with
u
and
v
, Bernoulli’s theorem leads
to a
z
-distribution of the hydrostatic pressure, over a vertical section, which depends
on the height
tyx
,,
]
of the free surface on which the atmospheric pressure
p
a
acts:
]
U
U
gpgzp
a
[6.47]
Relation [6.42] can thus be written:
22
const
2
* uv
g
t
s
s
[6.48]
We replace
]
in [6.46] with its expression taken from [6.48] in order to obtain
the potential
I
:
0
2
1
2
¹
·
¨
¨
©
§
w
w
'
V
tdt
d
g
I
]
I
[6.49]
6.2.6.2.
Analogy with a compressible fluid
Letting
]
gc
2
, we see that equation [6.49] can be written in a form identical
to equation [6.18] for the potential of a compressible fluid with two spatial

General Properties of Flows 287
dimensions. This equation, which is hyperbolic, represents the propagation of
surface waves of velocity amplitude
V
and height
]
Comparison between the corresponding equations [6.15] and [6.46] of these two
problems shows that the height
]
is analogous to the density
U
. However, the
expression for the velocity of sound
12
J
UUJ
kpc
of the compressible fluid
and that
]
gc
2
of the free surface indicates an exponent
J
equal to 2 for the
equivalent compressible fluid.
In physical terms, compressing a gas or elevating the free surface of a fluid
creates a reactive force in the form of a pressure increase (section 5.3.6) or of driving
pressure corresponding to the “elastic” energy of an oscillator. The hyperbolic
character of equation [6.49] leads to the existence of shock waves in the form of a
hydraulic jump ([YIH 77]).
6.2.6.3.
Influence of surface tension
We have previously assumed (section 6.2.6.1) the continuity of pressure across
the free surface. However, waves of small wavelength require surface tension
V
to
be taken into account. The pressure difference
V
G
p
due to surface tension is given
by Laplace’s law (section 2.2.1.4.2) which can be written by expressing the average
curvature, accurate to second order:
]V
]]
VVG
V
'
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
2
2
2
2
'
11
yx
RR
ppp
a
Condition [6.47] is replaced by:
]
V
]
U
G
]
U
U
V
' gppgpgzp
aa
Substituting into Bernoulli’s equation [6.42] gives the relation:
22
const
22
! Vp ! V
gz g
t t
'
ss
ss
which, associated with [6.46], gives a complex system which we will not study here
(see [YIH 77]).

288 Fundamentals of Fluid Mechanics and Transport Phenomena
6.3. Orders of magnitude
6.3.1. Introduction and discussion of a simple example
The mathematical variable properties of a continuous medium are relatively
regular. The equations governing a continuous medium assume the continuity and
the derivability to at least second order in the physical quantities, with the exception
of regions where shocks or discontinuities occur. The validity of physical models
(axioms of the continuous medium or models obtained from kinetic gas theory)
implies that the physical quantities observed are solutions of ordinary or partial
differential equations whose behavior is locally regular.
It is thus reasonable to admit that a quantity
f
undergoing
variations in the order
of
'
f on an interval of a time or space variable of length L
, possesses temporal or
spatial derivatives of the order of
Lf'
and that their second derivatives under the
same conditions are in order
2
Lf'
. Such a hypothesis should be subsequently
verified in discussing the results which can thence be obtained. The scale L
corresponds to the interval over which the function
f
varies. For example, for an
exponential function L is the characteristic dimension of the exponential variation
(space or time constant).
The preceding considerations result from the fact that a derivative is the ratio
limit of finite increases of the function and the variable, when the latter tends to
zero. It is clear that to within a factor of at most a few units, this derivative is equal
to the ratio of the finite increases in the region considered.
A partial differential equation (or an ordinary differential equation) is a
numerical balance between a certain number of terms containing derivatives. If this
equation only contains two terms, the absolute values of these are equal. On the
other hand, if the equation contains a sufficiently large number of terms, certain of
these are dominant in a given part of the domain, other terms being more important
in other regions. Each zone of the domain can thus be characterized by the locally
dominant physical phenomena.
Take the elementary example of the mass-spring oscillator with one degree of
freedom:
[6.50]
Suppose that we do not know the solution. We search first of all if a
characteristic time
W
exists for the phenomena described by this equation and
corresponding to a movement of amplitude
x
m
.
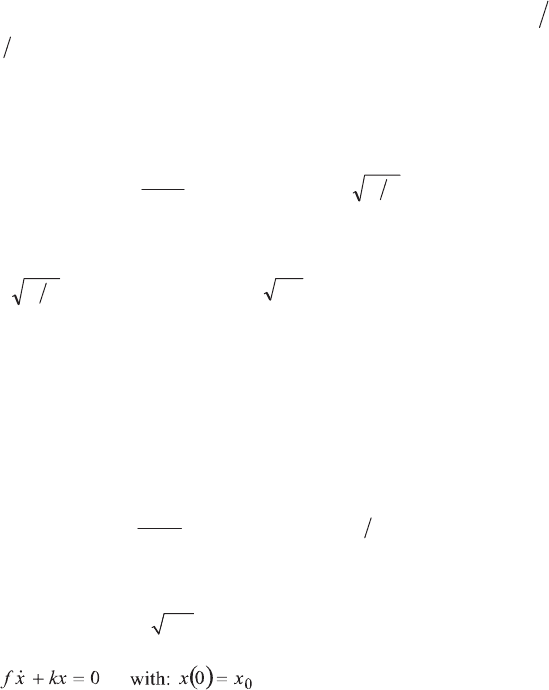
General Properties of Flows 289
The term
kx
of given order of magnitude
kx
m
is in the same order as at least one
of the other two terms of the equation which are, respectively:
2
W
m
mx
O and
W
m
xf
O .
Let us first suppose that
xf
is small compared to
kx
m
which is then of the same
order as
xm
:
kmxk
mx
xkxm
m
m
|
|
|
W
W
2
The characteristic time
W
necessary for the amplitude to vary from zero to
x
m
is
of order
km
and we also have
mkf
.
To first approximation, equation [6.50] can be written:
00 ;0 with: 0
x
x
x
kx
x
m
0
[6.51]
If, on the other hand, xm
is small, then it is the term xf
which balances kx ; we
thus have:
kfxk
xf
kxxf
m
m
|
|
|
W
W
The characteristic time
W
necessary for the amplitude to vary from zero to x
m
is of
order
/ , with ; fk f mkx
equation [6.50] thus reduces to:
[6.52]
The preceding order of magnitude analysis allows us to define the characteristic
time
W
for the phenomena described by the initial equation and to obtain an
approximate equation for this particular time scale. Simple general considerations
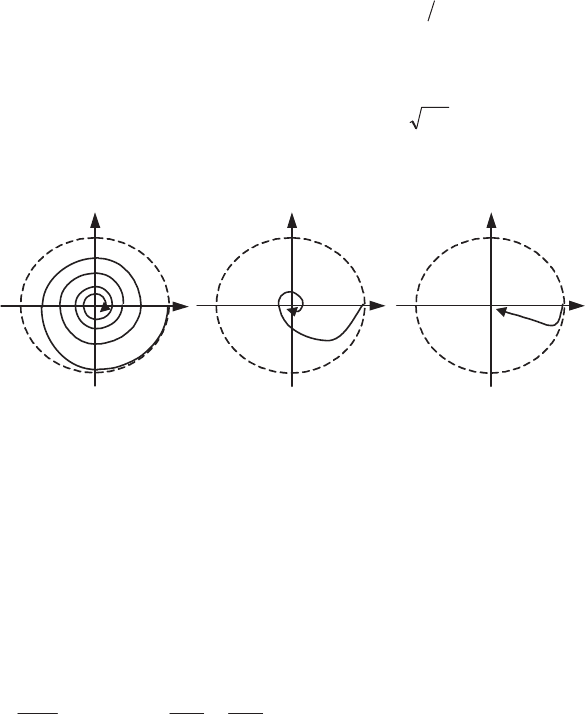
allow us to show that equation [6.51] represents an oscillatory movement, at least at
the scale
W
. For example, it is useful to discuss the equation in the plane (x, x
), often
referred to as the phase-plane. The trajectory [
txtx
, ] is there a curve
parameterized by the time and a simple qualitative discussion using equation [6.51]
allows us to easily see the form of this (Figure 6.10a), based on the fact that x
is the
derivative of x
, and its sign indicates the direction of the variation x
.
290 Fundamentals of Fluid Mechanics and Transport Phenomena
Equation [6.52] corresponds to a damped aperiodic movement. The trajectory in
the phase-plane is therefore a straight line with slope
fk . We will later discuss
the effect of the second initial condition
00 x
which obviously had to be
abandoned for the first order differential equation.
If we have equality in the orders of magnitude
mkf | , the three terms of the
equation must be conserved, but we will pass gradually from the form of Figure
6.10a to that of Figure 6.10c.
x
x
x
x
O
(a) (b)
x
x
O
(c)
Figure 6.10.
Evolution of the oscillator in the plane (x, x
): (a) oscillator with a small
damping; (b) damped oscillator; (c) aperiodic motion
(strong damping)
It then remains to study the influence of the small term neglected in each case:
this is a perturbation problem which we will discuss a little later (section 6.4). In the
first oscillatory case, we study the influence of friction with the balance equation for
the mechanical energy derived from [6.50] by multiplying by
x
and integrating
between 0 and t. We have, taking account of the initial conditions:
222
2
0
2
0
2
2
kx
kx
dtxf
xm
t
³
[6.53]
Equation [6.53] immediately shows the following properties:
1) kinetic energy is localized in the vicinity of the origin x=0;
2) potential energy is localized in the vicinity of the extrema of the stretching
motion;
3) kinetic energy can be transformed into potential energy such that the total
mechanical energy decays with time;
General Properties of Flows 291
4) dissipated energy
³
t
dtxf
0
2
is an increasing function of time; the result of this
is that the velocity must tend to zero if the integral is to remain finite; we can write
equation [6.53] in the form:
t
t
kx
x
m
dt
x
f
0
22
0
2
22
¹
·
¨
¨
©
§
³
[6.54]
Let
W
a
be the damping time of the oscillations; let
m
x
denote the maximum of
the velocity at the beginning of the movement which is considered only lightly
damped; this leads to the following orders of magnitude:
2
2
0
22
m
t
ma
xm
xfdtxf
||
³
W
From this we can derive the order of magnitude of the damping time:
f
m
a
|
W
.
It should be noted that the preceding considerations are concerned with orders of
magnitude which do not require an exact expression of equation [6.50]; they are in
fact valid for any equation whose terms have the orders of magnitudes posed above.
Therefore,
an approximate knowledge of results do not require complex
mathematical procedures above and beyond the numerical discussion about
monomes
(“rule of three”). By this procedure, which needs to be completed by a
discussion of perturbation problems, we can identify the important terms in a system
of equations, in other words, the dominant physical phenomena in each of the zones
of the problem domain. The order of magnitude of the unknown quantities can also
be deduced from this analysis.
6.3.2.
Obtaining approximate values of a solution
6.3.2.1.
Principles
Most particular functions (called “elementary” or “special”) are solutions of
linear equations with simple algebraic coefficients. For linear partial differential
equations (Laplace equation, wave equation, heat equation, Maxwell’s equations,
etc.), these functions are often useful in the search for solutions with particular
boundary conditions. As the equations of fluid mechanics are not linear, the
elementary or special functions are rarely directly useful.
Having simplified the equations and qualitatively discussed the various
phenomena, we can obtain approximate values in a simple manner by searching for
a
global solution in each zone where the equations can be simplified
. The method
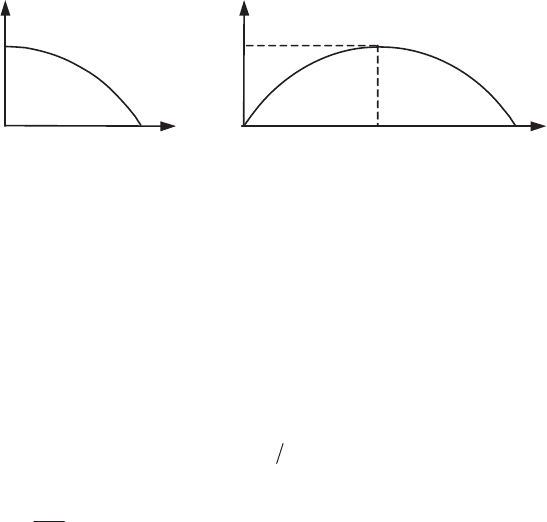
292 Fundamentals of Fluid Mechanics and Transport Phenomena
which we will use here can be generally applied, insofar as we suppose that we
ignore the exact solution of the equations, and that the particularities of the equation
linearity and the coefficient constancy are not used. The method consists in
searching for a global condition which can be obtained by integrating the equations
over each interval of the study. We then represent the form of the solution by a
plausible function in which the main unknown value is a parameter which we can
deduce from the preceding global condition. We will first apply this technique to the
preceding example of the oscillator.
6.3.2.2.
Global solution for the linear oscillator
Let us take for
W
the first instant where the abscissa
x
is zero (Figure 6.11a), the
velocity being then approximately maximum; this value
W
is more or less equal to a
quarter of the period
T
of the oscillatory movement. Let us consider equation [6.51]
with the conditions:
0;00;0
0
W
xxxx
[6.55]
t
x
(t)
O
W
x
0
t
tx
O
W
m
x
W
(a)
(b)
Figure 6.11.
(a) Law of motion during the first quarter of a period;
(b) variation of the velocity during half a period
Taking these conditions into account, the integration of equation [6.51] between
0 and
W
gives the global condition:
0
0
³
W
W
dttxkxm
[6.56]
First write the function
x
(
t
) which in the form
K
M
0
x
t
x
of a non-
dimensional function of the variable
W
K
t
satisfying [6.51] and conditions [6.55]:
2
0with 0 1, 1 0and 0 0
k
!! ! ! !
m
[6.57]
