Peube J-L. Fundamentals of fluid mechanics and transport phenomena

Подождите немного. Документ загружается.

General Properties of Flows 303

It is immediately verifiable from place to place that the functions

are variables

of separated functions and that they are proportional to the successive derivatives of

f(t):



)(

)

()

(

tfzygtzyu [6.71]

The functions )

( zyg

are solution of the system:

01021 1

1; ; ; ... , ...

ggggggg''' '



   

 

with the boundary conditions:

( , ) 0 ( , ) ; 0,1,..., ...

gyz yz C i n

 

The preceding equations can be solved successively with increasing i, and the

first equation corresponds to the Poiseuille flow (section 3.4.2.5). Let

= 1, which

amounts to taking

DT as a unit of time. The expression for the velocity

becomes:



)

(

)

(

)(

zygtfUtzyuUtzyu



The volume flow rate can thus be easily expressed as a function of the successive

derivatives of the pressure gradient:



sdzygtfUDsdtzyuUDq

)

(

)

(

)(22

Defining the dimensionless coefficients sdzygG

)

(

, it can be written in

the form:



)(2

tfGUDq

Let 'p(t) be the driving pressure loss for the length L; the pressure gradient can

be written in the form:



p '



and we have:



)(

304 Fundamentals of Fluid Mechanics and Transport Phenomena

From this we can derive an expression for the volume flow rate as a function of

the pressure loss and its temporal derivatives:

For example, in the case of a circular cross-section C (

) of

radius 1r



, we easily find:



113

1; ;

41644

119

3;...

256 9 9

gr r gr r

gr r r

¬







 











®

¬



















®



  





The physical interpretation of the series is not so simple, as the physical

significance of the higher order derivatives implies a long-term property. It suffices

to consider a function



tf and a polynomial approximation of this over an interval

of time. The higher order derivatives of these functions are very different, and so,

consequently, are the preceding corresponding series. In fact, we can easily verify

the convergence of the series for exponential or sinusoidal functions whose time or

frequency constants are relatively small, but the preceding representation is of

limited use for these particular cases.

For the example considered, we can show that we have convergence of the series

if the series of the general term



tf 4

converges. Recall, however, that, from

a mathematical point of view, the solutions established for the partial differential

equation does not require the existence of derivatives for the given function



tf .

The preceding results can equally be obtained by means of a Laplace transform

(Appendix 1) in the asymptotic approximation for large periods of time.

The regular perturbation of the solution to a non-linear partial differential

equation is more difficult (section 6.4.2.3), and in general we can only obtain the

first terms of the development. Examples of this kind of development (Blasius

series, Görtler series, etc.) are found for boundary layer equations ([SCH 99], [YIH

77]).

The method of regular perturbations can also be applied in acoustics and

energetics. Consider the geometry of Figure 6.13 in which the cylinder of base C is a

General Properties of Flows 305

solid, with constant physical properties, subjected to a heat release of volume power

P(t) and whose external wall is maintained at constant temperature T = 0.

The thermal conduction equation for this solid and the associated boundary

conditions:

;)( '

TtP

C OU

with: (,) : (,,) 0yz C T yzt

can be immediately reduced to equation and boundary conditions given in [6.69].

6.4.3. Singular perturbations

6.4.3.1. Introduction

In section 6.4.2 we assumed that the differential equation could be solved with

respect to the first derivative such that the unperturbed equation (

=0) possesses a

differentiable solution. This is not the case if the coefficient of the derivative tends

to zero with

faster than the other coefficients. Let us examine the elementary

example of the following differential equation in which the parameter

is now the

coefficient of the derivative )(tx



  

001)(' H xtxtx [6.72]

The solution is:

 

H ttx exp1.

For

to tend to zero, it is easy to follow the evolution of the solution towards its

discontinuous limit (Figure 6.12b) made up of the half-line (x = 1, t > 0) and the

origin O. Letting

H equal to zero in equation [6.72], we obtain the solution 1 x

which is valid nearly everywhere, and we can no longer satisfy the initial condition

posed at the origin for this part of the solution (called the external solution). We note

that the family of functions



,tx does not converge uniformly towards its limit for

= 0.

It is therefore necessary to perform a particular study over a small interval in the

neighborhood of the origin where the solution undergoes significant variations over

a small distance (internal solution) in order to recover the boundary condition which

is not satisfied.

The external solution can also undergo a regular perturbation due to the small

parameter

. For example, the solution of the following differential equation:



001 H  xxx



306 Fundamentals of Fluid Mechanics and Transport Phenomena

does only differs from the preceding equation by the coordinate 1 +

H of the

horizontal asymptote.

6.4.3.2.

Methods for studying singular perturbations

The existence of a singular perturbation is related to the presence of a singularity

for the limit solution of a system of differential equations. This phenomenon is

encountered in diverse circumstances and notably in the case of the lowering of the

order of a differential system in which we impose

as zero, or when the limit

solution or one of the derivatives involves a discontinuity on the interval of the

study. We will limit ourselves here to the study of a very simple case in order to

illustrate the general method by which we discuss such problems.

The direct numerical study of a problem involving singular perturbations often

presents difficulties on account of the very large disparity in the characteristic scales

found in different regions of the study. This point can obviously involve difficulties

for numerical methods in fluid mechanics. It is therefore particularly interesting to

directly obtain information independent of the exact solution (often very difficult) of

the differential problem which is posed. We will illustrate this using a very simple

case; the general analysis method involves a number of stages:

1) searching for the external solution: a study of the order of magnitude of the

solution which is assumed to vary regularly over the interval under study allows us

to obtain equations which are satisfied by the external solution;

2) we then try to identify a contradiction with respect to the data of the problem

in order to identify the singularity to study;

3) a new examination of the order of magnitudes of the terms of the equation

provides information pertaining to the scales of the singularity to be studied;

4) it is then possible to identify the equations of the differential problem in the

singular zone (internal solution), these resulting from simplifications of the

complete problem;

5) we then discuss the boundary conditions to be associated with the two

preceding problems for matching their solutions.

6.4.3.3.

An elementary example

The example of section 6.4.3.1 is too simple because the internal solution and the

exact solution are identical. Consider the following differential problem:

  

001)(   xttxtx



[6.73]

General Properties of Flows 307

Ignoring the results of the last example, let us apply the methodology described

above:

1) We first look for the external solution by supposing that the unknown function

has variations of the order of one on the intervals of the same order of magnitude.

), differential equation [6.73] reduces to:

ttx



1)(

The equation obtained is here an algebraic relation (a zero order differential

equation) which explicitly gives the external solution which is valid nearly

everywhere.

2) The condition that x(t) be zero at the origin is not fulfilled. We must therefore

complete the preceding solution by an internal solution on an interval with a

different scale to the interval where the external solution is valid, otherwise we will

only recover the latter. Let

be the order of magnitude of the length scale of the

interval over which the neglected term



must be taken into account.

The interval sought of scale

must be situated at the origin. In effect, if this was

not the case, we would have

between this interval

o(1)

and the origin a finite interval

on which the results of the external zone would be applicable; the function x would

be equal to 1+

t and would not therefore be zero at the origin, which would imply

that nothing had been solved. The only reasonable possibility is therefore to place

our small interval

in the neighborhood of the origin.

3) The order of magnitude of

can be obtained by supposing that the term

x' is

of the same order as that of the variations of x, i.e. of the order of 1:



|||

 

1)(

ttxtx



We can deduce from this that

H G

, and we need to study the behavior of the

solution in an interval of amplitude

close to the origin.

4) We perform the change of variable:

  

Xtx

Neglecting the terms of order

, equation [6.73] can be written:

 

001)(

 XXX



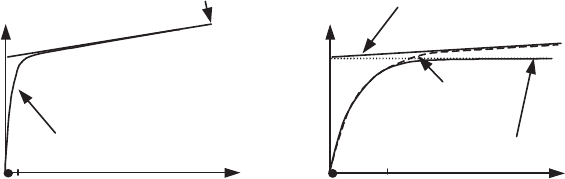
308 Fundamentals of Fluid Mechanics and Transport Phenomena

Its solution satisfying the condition at the origin can be written:









 eAX

It tends to A when

K

tends to infinity.

5) We now have two pieces of the solution (Figure 6.14b) which we need to

match. This procedure appears relatively empirical and we will consider only small

values of

. We see that as

tends to zero, the value

DH

1 of the external solution

for

tends to 1. We therefore adopt the following simple matching rule.

The limit of the internal solution

(

) for

becoming infinite is equal to the

limit of the external solution

(

t) when t tends to 0

 

t 0

limlim

ofo

(b)

internal solution:

1-exp(-t/

)

exact solution

external solution:

x = 1+



exact solution

H

(a)

H

asymptote: x = 1+



Figure 6.14.

(a) Exact solution of differential problem [6.73];

(b) matching of external and internal solutions

This rule provides the boundary conditions which were missing for the internal

solution and leads to a value of 1 being assigned to the constant

. We thus obtain

the internal solution:

( ) 1 with: /



X  e  t %



 

In fluid mechanics, the internal solution is called a

boundary layer

. Such

singularities are encountered in all domains of physics (skin effect in

electromagnetism, penetration depth of an evanescent electromagnetic or acoustic

wave, etc.). We will see other examples in problems of heat transfer or chemical

reactions with or without flow.

General Properties of Flows 309

The singularity can also consist of a discontinuity of the first or second

derivatives.

Perturbation problems can also present other characteristics. Consider for

example, the following lightly damped oscillator (section 6.3.1.1):

 xxx



The friction term



is a perturbation of the undamped equation. The

modification of the oscillatory solution due to a damping term

H

has an effect

of order



over a duration

O(1), but the final result is the suppression of the

movement. The perturbation effects due to friction are cumulative.

More complete developments on singular perturbations can be found in

specialized textbooks ([COL 68], [HIN 91], [NAY 81], [VAN 75]).

6.5. Quasi-1D flows

6.5.1. General properties

6.5.1.1.

Assumptions

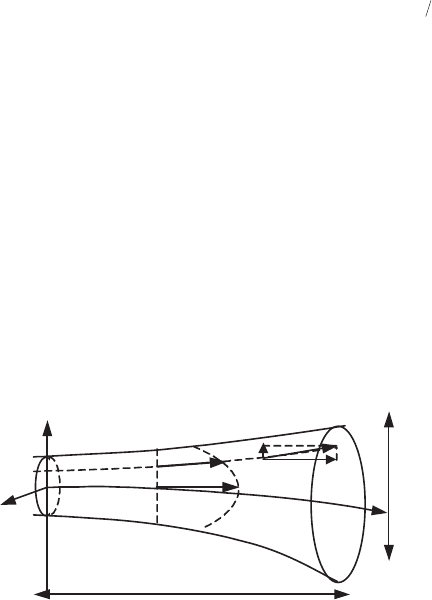
Many flows can present a quasi-1D character, in other words the evolution scales

of phenomena differ depending on whether we follow the principal direction of the

flow or the transverse directions.

Figure 6.15.

Quasi-1D flows

The basic assumption of a viscous quasi-1D flow is that the cross-section and

direction of a stream tube vary quite slowly (Figure 6.15). The thickness

of the

domain of study is small compared to its length

(

). We consider the

coordinate on a curve oriented along O

, more or less parallel to the stream tubes

(the axis of a pipe, jet or wall, etc.) and the orthogonal coordinates in cross-sections

310 Fundamentals of Fluid Mechanics and Transport Phenomena

orthogonal to O

. The local coordinates defined by the curvilinear abscissa

and the

orthogonal coordinates



, in cross-sections constitute a

coordinate system which

is locally Cartesian

. These assumptions allow us to write the

balance equations in

Cartesian form

in this zone.

We furthermore assume that the variations

G

of the quantities

studied are more

or less of the same order of magnitude over the distances

and

6.5.1.2.

Approximations

The following properties result from the preceding assumptions:

1) Partial derivatives of a quantity in the directions y or z are an order of

magnitude greater than the corresponding axial derivative in the direction Ox. In

effect

Lfxf

|ww

and

dfyf

|ww

lead to:

and

This results in vectors of the form k

fgrad (for example, the thermal or mass

flux densities

, etc.) are perpendicular to the axis Ox and that we only take into

account the two components k

yf ww and k zf ww of the flux density

2) The diffusion term

qdiv

 of the balance equation of a scalar quantity G is

therefore reduced to the sum of the transverse derivatives

ww

and

ww .

3) The transverse components v and w of the velocity are small compared with

the axial component u ( uv  and uw  ). In effect, assuming the flow to be

incompressible, the volume balance can be written:



If variations of the cross-section exist, the transverse velocity is not zero, but it is

very small, in order to ensure the inclination of the velocity with respect to the axis

Ox, of order d/L. Assuming the 2D problem (w = 0) in order to simplify matters, the

two derivatives

xu ww and yv ww have the same value (sign excepted). An order of

magnitude analysis shows that:

General Properties of Flows 311

i.e., sign excepted,

LUdv | .

No simplification is possible in the mass conservation equation.

The result of this evaluation of the velocity components is that the dominant

terms of the viscous stress tensor are the tangential components

yu ww

and

zu ww

(friction forces in the Ox direction).

4) The material derivative of a scalar quantity conserves its general expression

in the quasi-1D approximation.

Consider the material derivative



of the quantity g. The

two convection terms are of the same order:

GGG

5) On the other hand, an analogous order of magnitude calculation shows that the

small value of the transverse components of the velocity leads to the transverse

accelerations dv/dt and dw/dt

being negligible with respect to the axial acceleration

du/dt.

6.5.1.3.

Local balance equations

Taking account of the preceding approximations, balance equation [4.3] for the

volume quantity

g can be written:



gVdiv



 

[6.74]

By way of example, the dynamic equation following Ox [4.21], for a Newtonian

fluid, can be written:









PPUU

[6.75]

312 Fundamentals of Fluid Mechanics and Transport Phenomena

In a plane 2D flow, we obtain for a fluid with constant physical properties

(where p

is the driving pressure):







PUU

[6.76]

Finally, as the transverse accelerations dv/dt and dw/dt are negligible with

respect to the axial acceleration du/dt, the viscous stress terms of the transverse

equations are equally negligible with respect to the corresponding term in the axial

dynamic equation. The transverse equations reduce to:

The pressure (or driving pressure) distribution in a cross-section is hydrostatic,

but it depends on x and t.

Energy equation [4.51] can thus be written in the quasi-1D approximation:











OOVPP

[6.77]

Dissipation function [4.56] can be simplified by only considering the dominant

strain rates

yu ww and zu ww . We find immediately:



)

[6.78]

6.5.1.4.

Parabolic character of the quasi-1D equations

Consider first convection equation [6.74] in which the velocity field is assumed

to be given. This presents a structure analogous to the heat equation, i.e. it has a

dissymmetry in the order of the derivations with respect to the variables: second

derivatives with respect to y and z are encountered, the derivatives with respect to x

and t being only first order. This results in a parabolic behavior with respect to the

variables x and t: the temperature distribution in a cross-section of coordinate x at