Peube J-L. Fundamentals of fluid mechanics and transport phenomena
Подождите немного. Документ загружается.

General Properties of Flows 323
Finally, we must fix the initial upstream condition for the velocity distribution at
a given abscissa often taken as the origin
x
= 0. As we have explained in section
6.5.3.3, the stagnation point A of the flow of a inviscid fluid over the obstacle
(Figure 6.17) is the departure point of the boundary layer
that
can be easily
calculated in this zone where its thickness is quite small ([SCH 99], [YIH 77]).
If
the leading edge of the obstacle is of negligible thickness
(plane or wedge-
shaped wall), the thickness of the boundary layer is here taken to be zero.
6.5.3.6.
General properties of boundary layers
6.5.3.6.1.
Physical interpretation of the boundary layer
We can immediately note that
the condition of zero velocity on the wall also
leads to a condition of zero acceleration
. Conversely,
the viscous stress becomes
zero at the outer edge of the boundary layer
. This is therefore a zone where the
pressure gradient, which is constant, sees its action balanced by the acceleration in
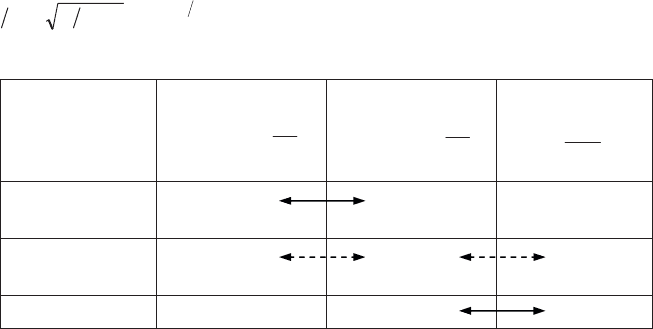
the outer region and by the viscous friction at the wall. This situation is shown
schematically in Table 6.1 which indicates the dominant terms following the height
in the boundary layer.
The solution previously obtained in section 5.4.5.4 for the heat equation is of the
same kind as that of the boundary layer, with time replaced by the
x
coordinate. The
zero-velocity condition imposed on the wall leads to
viscous diffusion of the viscous
stress and of the vorticity.
This results in an augmentation of the boundary layer
thickness as an abscissa function, as indicated by the order of magnitude
21
Re
|
L
ULL
UPG
found earlier [6.92].
height in the
boundary layer
acceleration
quantity
dt
du
U
pressure
gradient
dx
dp
viscous stress
2
2
y
u
w
w
P
outside (inviscid
fluid)
X X 0
inside boundary
layer
x X x
wall 0 X X
Table 6.1.
Balance of “forces” in the boundary layer
324 Fundamentals of Fluid Mechanics and Transport Phenomena
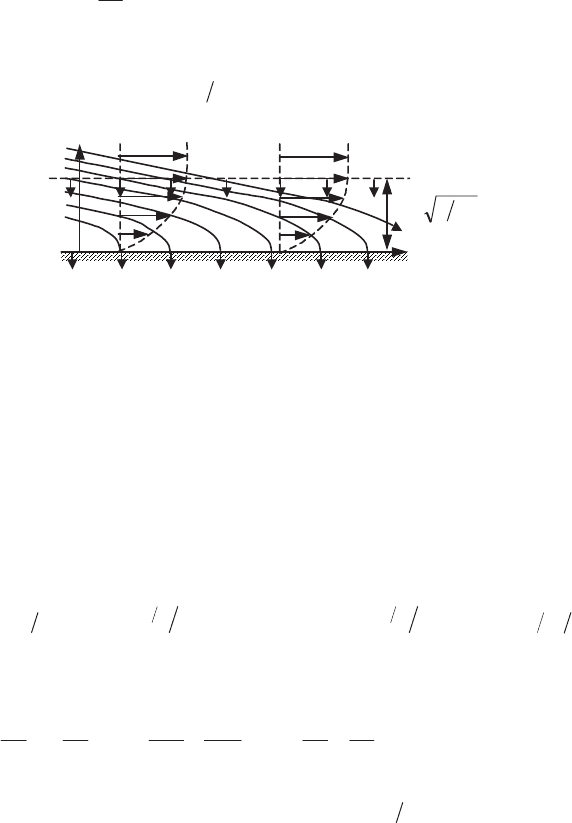
This diffusion can be counterbalanced by an aspiration of fluid across the wall.
Consider the simple case of a plane wall placed in a uniform flow of velocity
u
e
and
realize a suction of fluid across the wall at constant velocity
v
0
(Figure 6.18). We
see immediately that the solution:
¸
¸
¹
·
¨
¨
©
§
y
v
uu
e
Q
0
exp [6.96]
satisfies equations [6.91] of the boundary layer and corresponds to an established
solution where the thickness
0
v
Q
G
is constant. Figure 6.18 represents this flow.
x
u
e
0
v
QG
|
y
v
0
v
0
u
e
Figure 6.18.
Established boundary layer with suction
through a wall in an uniform flow
We note that in the case where we have blowing rather than suction (
v
0
positive), the solution is not acceptable: the boundary layer no longer exists if the
blowing is sufficiently strong ([SCH 99], [YIH 77]).
6.5.3.6.2.
Non-dimensional equations
Let us write equations [6.91] in non-dimensional form with the following change
of variables:
ULxuuLyReyLxxUvRevUuu
ee
~
~
/
~
~
~
2121
This gives:
0
~
~
~
~
;
~
~
~
~
~
~
~
~
~
~
~
2
2
w
w
w
w
w
w
w
w
w
w
y
v
x
u
y
u
xd
ud
u
y
u
v
x
u
u
e
e
[6.97]
Equations [6.97] do not contain the parameter
P
U
UL
Re . This results in the non-
dimensional solution
being independent of the Reynolds number
. So, all bodies which
have the same form have identical velocity distributions
xu
e
~
~
at the wall; they therefore

General Properties of Flows 325
have the same boundary layer development. We note however that the Reynolds number
comes into play as soon as we recast the problem using dimensional data for the
coordinate
y
and notably for the thickness of the boundary layer (formula [6.92]).
6.5.3.7.
Separation of steady flows
The preceding discussion shows that, in the external part of the boundary layer,
the flow is close to the flow of an inviscid fluid where the pressure gradient is
determined by Bernoulli’s theorem: the modulus of the velocity decreases if the
pressure increases.
Close to the wall, the weak kinetic energy no longer plays an appreciable role
and the variations of the viscous stresses are opposed to the pressure gradient in the
boundary layer equations. The flow which is nearly purely viscous close to the wall
results from two causes:
1) The
pressure gradient
leads to a tendency of the flow towards decaying
pressures as in a Poiseuille flow (section 3.4.2.5). The velocity curvature profile at
the wall is equal, according to [6.91] and [6.95] to:
dx
du
u
dx
dp
y
u
e
e
e
y
Q
U
P
w
w
1
0
2
2
2) The
external velocity
xu
e
imposed creates a viscous entrainment in the
boundary layer in a manner analogous to the corresponding phenomena in a Couette
flow (section 3.4.2.3).
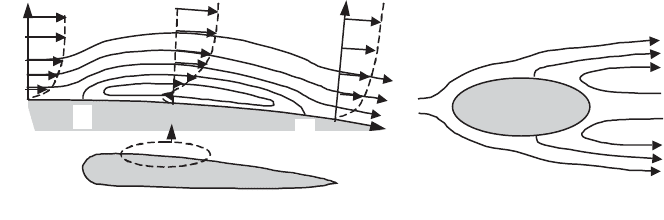
When the flow external to the boundary layer
xu
e
increases with the abscissa
x
, the longitudinal pressure gradient is negative and the velocity curvature profile
has a constant sign (Figure 6.19a). In the opposite case (Figure 6.19b), the sign of
the curvature of the profile changes, and this can lead, close to the wall, to a flow
which is reversed with respect to the external flow
xu
e
.
(a) dp/dx < 0
(b) dp/dx > 0
x
x
u
e
(x) increasing
u
e
(x) decreasing
Figure 6.19.
Velocity profile near the wall with a
(a) negative or
(b) positive pressure gradient
326 Fundamentals of Fluid Mechanics and Transport Phenomena
The appearance of a flow from downstream to upstream is in
contradiction with
the parabolic properties
of the boundary layer equations: the velocity distribution in
the zone of reversed flow no longer depends only on the upstream conditions the
external velocity
u
e
(x) considered, but also on the downstream conditions. The
boundary layer equations are thus no longer applicable in such a zone.
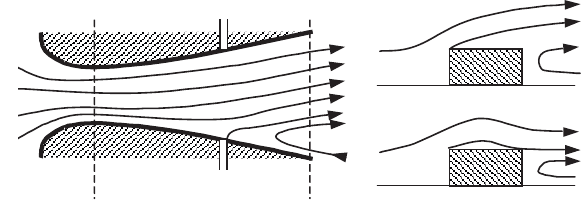
y
S
R
(a) (b)
wake
rotational
Figure 6.20.
(a)
Separation with reattachment in the boundary layer (profiled obstacle);
(b) separation and creation of an open wake (unprofiled obstacle)
There therefore exists a back stagnation point S in a viscous flow where the
friction stresses on the wall are zero (Figure 6.20a). In fact, the flow, which is
reversed with respect to the main flow, comes from a rotational zone which can be
manifested in two forms:
– either a relatively thin rotational zone is generated within the boundary layer,
but reattaches at point R (Figure 6.20a); following what was said above, this can
only happen if the effect of the pressure gradient is sufficiently weak for the viscous
entrainment to constitute the dominant effect. This is the case for
profiled obstacles
whose reducing section in the downstream direction is very gradual;
– or a completely open wake can be generated downstream of an obstacle which
is not profiled (Figure 6.20b).
Note that the
position of the separation point is independent of the Reynolds
number
, provided the velocity distribution of the inviscid fluid at the wall does not
depend on the Reynolds number either. This is the case for the irrotational inviscid
fluid around a profiled obstacle which is not modified (to second order) and
obviously does not depend on the viscosity. For the unprofiled obstacle, the real
velocity field is different from the field calculated in an inviscid fluid on account of
the presence of a rotational wake which is fed from downstream; however, if we
assume that the structure of this wake is independent of the Reynolds number, we
see that it is consistent to assume that the position of the separation point is also
General Properties of Flows 327
independent of this parameter: this is confirmed by experiments,
provided the
boundary layer is not turbulent
([SCH 99], [YIH 77]).
6.6. Unsteady flows and steady flows
6.6.1. Introduction
The temporal evolution of the properties of matter is fundamentally based on the
balance laws of the associated extensive quantities. We have already discussed in
Chapter 2 the difficulties of representing the continuous medium which we
encounter depending on whether we choose to use a Lagrangian (substantial)
description of the fluid particles or a Eulerian (spatial) representation of the flow.
We must now return to the fundamental difficulties which arise when we use
Eulerian variables.
The fields to which matter is subjected are furthermore always due to actions at a
distance performed by other material elements: a gravitational field is caused by the
presence of mass, an electric field results from the presence of charges, an
electromagnetic field is due to electric charges in movement at either the
macroscopic or the microscopic scale. A field is described by functions of space-
time variables in a reference frame (known as the laboratory reference frame)
associated with a flow device or an object moving with respect to a fluid (vehicle,
plane, etc.). There are numerous situations for this observer in which the velocity
fields and the material quantities are not functions of time, but only of space. The
corresponding phenomena are therefore steady. This
terminology only has meaning
in reference to this privileged reference frame, the quantities attached to the
material particles being always functions of time
(Lagrangian representation).
However, these steady phenomena, when they exist, always arise as a result of
the evolution of a transitional regime. Thus, in many situations, the transitional
regimes do not lead to steady flows and we observe complex phenomena which we
will describe very briefly here.
In order to simplify the discussion, we will consider in what follows
an inviscid
or Newtonian fluid of constant density
, unless otherwise stated. The variations of the
physical properties, if they are not too great, do not significantly modify the
structure of the phenomena which we will discuss.
We will leave aside questions related to the existence and to the uniqueness of
solutions of the Navier-Stokes equations, the understanding of which requires a
more advanced course in mathematical analysis. In this domain many questions

328 Fundamentals of Fluid Mechanics and Transport Phenomena
remain open, and the physical aspects of the phenomena which we describe in this
textbook demonstrate the formidable complexity of such an eventual theory.
6.6.2. The existence of steady flows
For a flow and the associated transfers to be steady, it is necessary for the
boundary conditions describing the corresponding problem to be steady; in
particular,
actions on the flow by fixed elements in this reference frame should be
independent of time. For example, the flow between upstream and downstream
infinite reservoirs at constant pressure and connected by a nozzle (section 5.5.4) can
be independent of time if the system is described in the reference frame of the
nozzle. However, before being observed at a given flow rate, the flow was created
from a zero pressure difference and it followed an evolution through the following
states: a subsonic regime with increasing velocity, then a sonic regime and finally a
supersonic regime with the progressive appearance of a shock wave which descends
in the divergent part of the pipe until the pressure gradient is stabilized.
The solution of the problem defined by the steady boundary conditions is not
always unique. The nature of the boundary conditions to be used is often a source of
considerable difficulty (section 5.6.3). Consider for example the flow between two
cross-sections
S
1
and S
2
(S
1
> S
2
) in a divergent pipe (Figure 6.21). Under the
assumption of an inviscid incompressible fluid and with the approximation of the
flow by slices, Bernoulli’s theorem can be written:
22
2
2
2
2
1
1
U
p
U
p
U
U
The flow rate
VSq
v
U
in this section of the pipe can be immediately
obtained:
p
2 1
B
p
q
v
r
U
22
21
11
with: .
22
B
SS
There exist two opposite flow rate values for this steady flow. We will see later
that only one of these is really acceptable in the context of the preceding
assumptions.
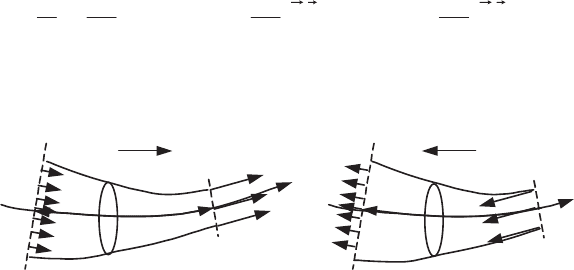
Let us now perform an experiment with a plane pipe whose divergent has a
sufficiently large angle (of the order to 10 degrees or so). Here we observe that the
steady flow follows one of the walls while it separates from the other. The flow
chooses the wall to follow as a result of particular circumstances of the transitional
General Properties of Flows 329
regime. For example, in the configuration in Figure 6.21a, we have included in the
walls two suction orifices A
1
and A
2
which are not activated in the steady regime
and which we can use in order to create a small additional transitional depression in
order to “suck” the flow towards a chosen wall. This suction does not need to be
constant: once the flow has attached to one of the walls, it will remain so after the
suction has been stopped. Such flows with two stable positions can be used to
control flows in fluid circuits (fluidics command and control).
suction orifice A
2
suction orifice A
1
S
2
S
1
p
1
p
2
(a) (b)
Figure 6.21.
Steady flows with two configurations
For the two preceding flows, the pressure is nearly constant in each of the
sections S
1
and S
2
. Writing the boundary conditions for the steady flow of a viscous
fluid leads to considerable difficulties, because there no longer exists a velocity
potential and we know that we cannot independently specify the entry and exit
conditions of a flow since the transport properties on the trajectories are dominant
(section 5.6).
Figure 6.21b shows another configuration where two flow structures in a pipe are
possible depending on whether the flow reattaches or not on an obstacle placed on
its wall. The existence of reattachment is also related to the transitional regime
which leads to the fully established flow. Examples of the same kind exist for sheets
of water over spillways, which may flow above cavities either ventilated (i.e. filled
with air) or not ([CHA 04] p. 399, [JAI 01] p. 264).
The preceding problems are examples of systems presenting hysteresis (the state
of a system depends on its history). From a physical point of view, we can note that
we have here a “retroaction” in the upstream direction which leads to the existence
of a memory for the flow.
330 Fundamentals of Fluid Mechanics and Transport Phenomena
In summary, a flow problem with steady boundary conditions does not
necessarily have a unique steady solution. We could also say that a steady problem
is not necessarily a well-posed problem.
6.6.3. Transitional regime and permanent solution
6.6.3.1.
Relation between pressure and flow rate in a fixed stream tube
Depending on the imposed conditions, pressure can be the cause or the
consequence of movement of a fluid. Aside from cases where the viscosity plays a
dominant role (low Reynolds number flows), the pressure (or the driving pressure
depending on the case) balances the acceleration, and for steady flow of an inviscid
fluid, Bernoulli’s first theorem treats the pressure (or the total enthalpy) as a
component of the total mechanical energy which is conserved for a fluid particle.
This local property no longer exists in unsteady flows.
Consider the flow of an inviscid fluid of constant density whose fluid trajectories
are fixed; they are thus coincident with the streamlines (and the emission lines). A
stream tube is therefore a surface on which the inflow and outflow of fluid occurs
over the cross-sections S
1
and S
2
with velocities V
1
and V
2
(Figure 6.22). The
assumption of incompressibility leads to a volume flow
SVtq
v
circulating in
the stream tube which is independent of the cross-section used to evaluate it; we will
treat it thus as a variable. Let us apply kinetic energy theorem [6.85] to the interior
domain D of the stream-tube element limited by the surfaces S
L
, S
1
and S
2
(Figure
6.22); we have:
³³³
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
w
w
DSS
dsnV
V
pdsnV
V
pdv
V
t
12
0.
2
.
22
222
UUU
where p designates the driving pressure by way of simplification.
A
q
v
q
v
S
1
S
1
S
2
S
2
p
1
p
1
p
2
p
2
B
>0
1
V
G
1
V
G
2
V
G
2
V
G
A
S
S
(a)
(b)
S
L
S
L
L
L
Figure 6.22.
Flow by slices inside a stream tube:
(a) convergent tube; (b) divergent tube
General Properties of Flows 331
In the slice approximation of the flow, the quantities are uniform in all cross-
sections, and after simplification by q
v
, we immediately obtain:
0
22
12
2
1
2
2
0
¸
¸
¹
·
¨
¨
©
§
³
pp
UU
S
d
dt
dq
L
v
UU
A
Let:
³
L
S
d
A
0
U
A
and
¸
¸
¹
·
¨
¨
©
§
2
1
2
2
11
2
1
SS
B
U
The relation between the flow rate q
v
and the pressure difference p
1
p
2
can be
written:
21
2
ppqB
dt
dq
A
v
v
[6.98]
This equation shows that the pressure is balanced by two acceleration terms, one
unsteady,
dt
dq
A
v
, and the other,
2
v
qB , corresponding to the steady flow,
proportional to the square of the flow rate and independent of the direction of the
flow. This separation is related to the Eulerian description of the phenomena, and
from a physical point of view there are not two kinds of acceleration for the fluid
particles. As we have already said (section 3.3.3.5), this description is always
associated with a favored reference frame resulting from the existence of boundary
conditions on the particular surfaces which are here the sides of the stream tube.
We should note that the coefficient A of equation [6.98] has an order of
magnitude proportional to the length, contrary to the coefficient B which only
depends on the values of the inflow and outflow sections. Furthermore, the 1/S
dependence of the integral A shows that a severe intermediate narrowing will not
modify the values S
1
and S
2
but will lead to a considerable increase of the coefficient
A, in other words to the pressure difference necessary for the transitional
acceleration in the Eulerian representation. The reason for this is the existence of a
strong acceleration in sections of small dimension where the velocity takes on high
values in order to conserve the flow rate.
6.6.3.2.
Properties of the solutions
Let us take B to be positive (
21
SS ! ), which does not restrict the generality of
the reasoning. Equation [6.98] can only therefore possess steady solutions if the
difference p
1
p
2
is positive. In this case, we have the two steady solutions
332 Fundamentals of Fluid Mechanics and Transport Phenomena
Bppq
v
21
r , corresponding to an established flow, either in the positive
direction, or in the negative direction of the axis
A
(section 6.6.2). However, the
possibility of realizing such a solution depends on the existence of a transitional
regime which can lead to this kind of situation.
In the unsteady regime, the pressure difference p
1
p
2
can be negative. However,
an examination of equation [6.98] shows that if it is always negative, the same goes
for the derivative
dt
dq
v
; we can thus see that the flow rate q
v
decays indefinitely,
which is physically unacceptable.
Suppose now that the difference p
1
p
2
is positive and let
BpptQ
21
; Q(t) is the positive value of the flow rate under the
assumption that the unsteady term is negligible. Equation [6.98] can be written:
22
v
v
qtQB
dt
dq
A [6.99]
We see that:
– if the instantaneous flow rate q
v
is greater than Q(t), the derivative
dt
dq
v
is
negative: the flow rate q
v
decays and approaches the value Q(t);
– if q
v
lies between – Q and + Q, it therefore increases, and approaches the value
Q(t) once again;
– if the instantaneous flow rate q
v
is less than Q(t), the derivative dtdq
v
is
negative: the flow rate q
v
decays and moves away from the value Q(t).
This property leads to the flow rate being bounded if the positive quantity Q is
bounded. If Q(t) tends to a limit for infinite t, the same goes for the instantaneous
flow rate q
v
if the latter remains always greater than – Q. Under the assumption of
constant pressure difference p
1
p
2
, we see that the transitional regime does not
allow the solution
BpptQq
v 21
to be attained.
The inviscid fluid model does not apply for negative flow rates, and the viscosity
must be introduced. The study of viscous fluid flow between two infinite divergent
planes can be performed (the Jeffery-Hamel exact solution of the Navier-Stokes
equations). We find that a separation occurs for a Reynolds number which tends to
