Peube J-L. Fundamentals of fluid mechanics and transport phenomena

Подождите немного. Документ загружается.

Measurement, Representation and Analysis of Temporal Signals 353



(answer:

s ''

 '

In the second case, we see that if b is equal to 2a, the measurement of a does not

cause any uncertainty in s (to second order). The function s thus presents an

extremum with respect to the variable a, making it stationary. The situation is thus

quite optimal for measuring the quantity s. In general, expression [7.1] shows that

the lower the sensitivity of the quantity measured to the variations of the

measurement parameters, the better the precision of the measurement. Note that

systems that are close to instability are particularly sensitive to perturbations and

that the measurement of associated quantities is thus particularly difficult.

These elementary ideas are sufficient in simple cases. However, they must be

completed in the case of complex measurements requiring a large number of

unknowns and of quantities to be measured.

7.2.7.3.

Errors and conditioning of a linear system

These ideas of errors and uncertainty have been broadly studied for the

numerical solution of linear systems of various sizes. The development of computer

technology has led to the possibility of measuring large numbers of quantities

simultaneously and of deducing interesting physical quantities by solving the

equations that characterize the measurement process. The problems posed here are

identical to those encountered in the numerical study of systems of equations

obtained from modeling.

Let us assume that the evaluation of a vector quantity X is performed via the

measurement of another vector quantity B of the same size. The vector of unknowns

X and the vector of given data B are assumed to be related by a linear system in

which the square matrix A models the measurement process:

[7.2]

As we are here interested in discussing errors that are assumed small, the linear

system can always be obtained by linearizing the equations about the experimental

conditions and the matrix

A is constant. It is invertible (otherwise the measurement

is not meaningful). The precision which can be obtained for the solution

1

depends on the sensitivity of the system: if a small variation in the right-hand side

B leads to a large variation of the solution, we must expect poor precision in

obtaining the solution. We quantify the idea of sensitivity by means defining the

condition number



of the matrix A by the relation:

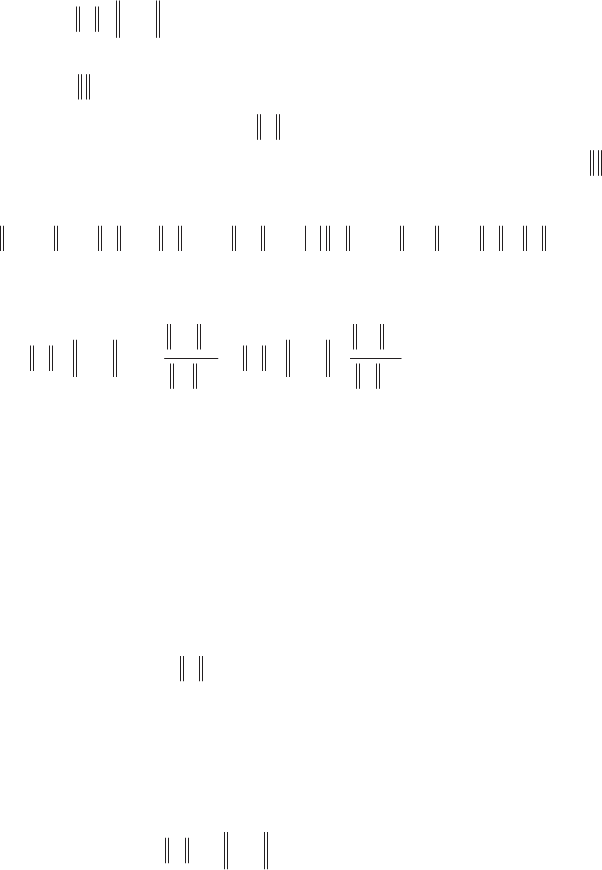
354 Fundamentals of Fluid Mechanics and Transport Phenomena



AAA

1

The symbol

. designates a matrix norm defined most often by means of a

vector norm. For example, the norm

of the matrix A is the maximum value

taken as the sum of absolute element values of each column of A. A norm

satisfies the conditions:

pppppppp

BAAAABABA .B.;.; dO Od

Using this condition, the reader can easily verify the following inequalities:

.;.1



This inequality shows that the condition number



constitutes an upper

bound of the relative amplification error between the data

B and the unknown X in

solution of system [7.2]. The greater this value, the greater the sensitivity of the

solution to variations in

B. The precise condition number value depends on the

choice of the norm.

A well-conditioned system (



of the order of 1) allows the

obtention of a good accuracy in the solution.

In order to illustrate the influence of the condition number we will consider a

rudimentary example where

X has two components. Consider the matrix A with

which we associate the norm

A (defined above):

A [7.3]

The reader can certify that we obtain:

  

1;1;

DND

 





AAAA

hence:



BAX

[7.4]

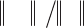
Measurement, Representation and Analysis of Temporal Signals 355

When D is equal to 0, the system is perfectly conditioned (



N A ). In this

case the solution is the identity (

), or: (



2211

, bxbx ). We thus directly

measure the unknowns, which is ideal.

On the other hand, for 100

D , we have an ill-conditioned system and small

variations of measurement

B can lead to large variations in solution X. The reader

can easily verify that, for the preceding example, changing the vector

B from:

100

will cause solution

X to change from

100

: a variation of

1% in the modulus of the inputs data

B leads to a variation of a factor of 100 in the

vector

X, which has also rotated by 90°. They can also calculate the relative

variation

XXG of the solution and that of the right-hand side, in addition to

the amplification factor of the relative error between

B and X.

These considerations show that the conditioning of a linear system of equations

deteriorates as its matrix becomes filled and its coefficients are large. A full matrix

of large size is thus very poorly conditioned.

Poor conditioning can be improved by a suitable change in the way the equation

is written. The system of the last example [7.3] is optimal. The system of the last

example [7.3] can be written in the solved form [7.4] whose conditioning is optimal.

The accuracy problem has not been resolved however, as we see that it is the

quantity

b b



which must be measured directly with good precision. Changing

the way the system of equations is written without changing the measurement

method clearly improves nothing.

In conclusion, this idea of conditioning is essential in order to appreciate the

quality of an experiment, a model or a numerical processing of information.

Considerable theoretical and practical progress has been made in this domain. We

refer the reader to [DEM 97], [PRE 07] and to manuals of computation tools

(MATLAB for example; instructions “cond” and “condest”).

7.2.7.4.

Consequences for measurement techniques

In general, the evaluation of a quantity is effected by measuring other quantities

that are related to the first by relations that characterize the measurement procedure.

The matrix

A of the corresponding system of equations must be well conditioned in

order that the uncertainty is as small as possible. In cases of poor conditioning of the

matrix

A, the very principle of the method of measuring the unknown quantities is

questionable and needs to be modified. In simple terms, the preceding example

amounts to saying that if two measurements are determined for the most part by

means of a single quantity, it will not be possible to obtain an indication of the value

356 Fundamentals of Fluid Mechanics and Transport Phenomena

of another quantity with good accuracy and it will be necessary to change the

measurement method.

For example, uncertainties always accumulate for independent measurements;

we should always avoid obtaining the value of a quantity

g by means of the

difference in measurements between two much larger quantities. Thus, the value for

a small air velocity is obtained using Bernoulli’s theorem from the pressure

difference

p between two cross-sections that are quite close together, but of

different sections. It is clear that

p should be directly measured by means of a

differential manometer which is directly sensitive to this pressure difference and not

from the independent measurement of two pressures.

In general, the quantities measured should be in the same order of magnitude as

the unknown. Let us take another example, the propagation velocity

c of sound

signals with respect to matter is large (about 340 m/s in air or 1,500 m/s in water). If

the matter is in movement at velocity U (a few m/s), a signal emitted at A (Figure

7.6) will arrive at B (AB parallel to the velocity;

dAB ) with a delay equal to



Ucd  , whereas a signal emitted at B will arrive at A with delay of



Ucd  .

The separation

between the propagation times of the two signals is thus equal to





2 UcUd  . In principle, the measurement of

allows the measurement of the

flow velocity

c+U

c-U



Figure 7.6.

Direct measurement of the delay between the arrival

of two synchronous signals in A and B

However, it is important not to measure the propagation times of the two signals,

but rather the time separation

W

; for this the two signals should be emitted

simultaneously, and the time difference can be measured for example by starting a

stopwatch when the first signal arrives. Proceeding in this way, errors of

discretization and digitization which are only concerned with a reduced value

rather than much larger values will be avoided (in accordance with the ratio c/U). If

the measurement were performed by means of analogous measurement devices, the

Measurement, Representation and Analysis of Temporal Signals 357

conclusion would be the same, as these have a relative accuracy, which is associated

with the scale of the measurement.

In general, methods which involve ensuring that the quantity measured is zero in

conditions very close to those in which we operate are known as zero methods. The

electric-bridge methods used (Wheatstone bridge, etc.) to measure impedance are

well-known zero methods.

7.3. Representation of signals

7.3.1. Objectives of continuous signal representation

7.3.1.1. Introduction

We have seen in the preceding chapters how a physical system can be

represented by a continuous medium or modeled by associating components in a

state of thermodynamic equilibrium. We have limited ourselves to thermodynamic

aspects without really discussing the “quantity of information” necessary for

knowledge of a system. This idea is quite difficult to define, as it depends in fact on

the complexity of the system, the degree of approximation which can be tolerated in

this knowledge, the sensitivity of the system towards perturbations and the way the

information is structured. We have only indicated that the number of variables

necessary is greater as the thermodynamic imbalances are more pronounced.

The continuous medium described in Chapter 2 is an indispensable mathematical

limit wherein the equations describe the observable macroscopic properties,

provided that the associated physical quantities have been included. In order to aid

the discussion, we will assume that the physical system and its appropriate model

(for example, the Navier-Stokes equations) are equivalent models: results obtained

from each should be identical (Figure 7.7). It is clearly an optimistic departure point,

but one which can afterwards be tempered by taking account of the errors associated

with the choice of models, the measurement procedures, the numerical methods of

calculation, etc.

The solutions of the theoretical model and the physical quantities of the

corresponding experiments possess the same properties of continuity and

differentiation. The representation of these solutions and quantities is the first

practical problem to be solved. In what follows, we will limit ourselves to a

function of one variable, which is for instance a temporal signal.

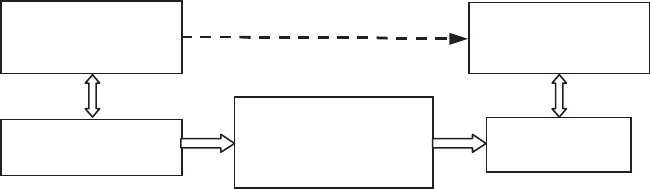
358 Fundamentals of Fluid Mechanics and Transport Phenomena

Boundaries conditions

of model

Continuum model

equations Hf=

(Navier-Stokes, for

example)

Solution f

Data

physical problem

(Inputs)

Results S of

physical problem

(Outputs)

Physical problem

Figure 7.7. Physical system and its mode

In a procedure adopted over many years, any solution to the equations of

continuous media, mechanical or electrical, are presented in the form of an

analytical representation from which it is possible to calculate the value of a

measurable global quantity, for example the flow rate in a pipe as a function of the

pressure difference applied, the value of an electrical resistance of a conductor of a

given form, the thermal flux resulting from a temperature difference imposed

between two external surfaces of a medium, etc.

Thus, experiments have for a long time consisted of measuring certain local or

global quantities which allow the validation of the model of the system studied. The

appearance of computer techniques has not really changed this manner of

proceeding, but it has allowed us to increase to an extraordinary extent the power of

the means by which we compute quantities in the model. Progress in analog and

numerical electronics has also allowed instantaneous measurements that were

previously unimaginable. We thus find ourselves today confronted with an

enormous quantity of information contained in the results of numerical

computations or measurements, which need to be processed in as rational a manner

as possible. These new technologies have radically changed both the way in which

results are represented and used. Beyond these practical aspects, the comprehension

of physical phenomena has been profoundly modified. An analogous mutation was

produced at the beginning of the 19

century with the introduction of the Fourier

series.

Finally, the problem representing a function arises both from the point of view

of analysis and storage of measurement data, and that of the analytical or numerical

resolution of modeling problems. The numerical calculation of solutions of

differential equations was obtained either by performing finite difference

calculations or by means of tables, these having been calculated for discrete values

of the variables. In practice, these procedures required important and careful effort;

only the use of numerical tables was familiar to the physicist or engineer who was

mostly happy to calculate a numerical value by interpolation between two values of

a table.

Measurement, Representation and Analysis of Temporal Signals 359

In this chapter, we will limit our discussion to general procedures for

representing signals; the problems of representation associated with modeling will

be discussed in Chapter 8.

7.3.1.2.

Objectives of signal representation

In these conditions, the first question to be considered concerns the practical

utility of a field of a continuous quantity

and the reasons for using it. The model of

Figure 7.7 is a

knowledge model, which allows us to know everything about the

problem that is posed. It contains variables which are continuous functions of time

and which represent quantities of the associated physical system.

A variety of different reasons lead to the representation of a temporal signal:

– we can firstly

analyze it, in other words obtain information which allows us to

understand the physical process and eventually to modify it;

– the signal can also be

recorded in its totality with a view to later use;

 we can also extract more or less condensed information from this signal that

we will keep for a later, significant, signal restoration;

– in certain cases, we would like later to construct physical synthetic signals:

music synthesizers, speech or image synthesizers, modeling of real devices by

numerical simulation on computers, active control of phenomena, etc.;

– finally, we can perform a signal transformation by applying to it an algorithm

with the objective of computing another signal.

Depending on the objective in mind, the nature and the quantity of the

“information” which we intend to conserve and use, we proceed differently. In fact, we

often find ourselves confronted by a double problem of storage and/or of interpreting

information contained in a physical signal. Conserving billions of numerical values

without understanding what they represent is not very helpful; this operation has a

certain associated cost, even if this is becoming less and less. In certain difficult and

expensive experimental cases, it is of interest to conserve large masses of data, which

is possible using modern equipment, in the hope that we will know how to extract

pertinent information which we do not know how to extract at the moment of the

experiment; but the difficulty is storing the data in a suitable form.

With the exception of measurements performed with a specific objective, any

representation of a function of time

s(t) should allow the signal to be recalculated. The

practical needs associated with the storage and reproduction of information concerns

all domains; beyond science and technology, the conservation of music, speech and

image (for historians, etc.) has a social interest. Signal processing is a complex

discipline that we will not consider in detail; the reader should refer to specialized texts

360 Fundamentals of Fluid Mechanics and Transport Phenomena

([BAH 01], [CAS 06], [JAC 91], [MEA 91], [PRI 91]). We will here only give certain

general indications, which should allow the reader to appreciate the information

processing problems that arise in the treatment of physical phenomena encountered in

acoustics, fluid mechanics and thermodynamics.

7.3.2. Analytical representation

A signal s(t) can be represented by a simple “analytical” function, in other words

a compact expression which defines a process at each instant of an interval of study,

either by means of predefined functions such as circular functions, polynomials,

Bessel functions, etc. or by means of formulae which imply one or many known

methods (integration, differentiation, convolution, etc.). The “analytical” term is not

here to be taken in the strict mathematical sense, despite the fact that the function

used can satisfy the mathematical definition of analyticity.

This analytical representation, exact or approximate, can be obtained in different

ways:

– an exact explicit solution of a system of equations that constitute a model,

although in practice this is rarely possible for continuous media in flow;

– an approximate global solution of the same system of equations by a procedure

which consists of satisfying the averaged equations (weak solution). Different ways

of proceeding exist; for example, we can replace the equations with integral

conditions which constitute a simpler system of equations containing fewer

variables and to which it is possible to find an analytical solution (see elementary

examples discussed in sections 6.2.6, 6.3.1.2 and 6.5.2.2) or a solution of a form

which is given

a priori and for which certain coefficients can be obtained by least

square methods (error minimization, etc.);

– interpolation functions (polynomial or other function) obtained from punctual

measurement data, graphical recordings, etc.

The analytical representation of a signal

s(t) thus consists of defining the class of

functions used and the parameters that characterize this particular function. In

general, predefined elementary or special functions allow a particular synthetic

knowledge, which a numerical representation does not provide. Knowledge of their

properties often allows interpretations of the solution thus obtained and reasoning

regarding the relations of cause and effect by means of known analytical properties.

It is thus possible to derive particular properties or other analytical forms without

any numerical computation in the context of the theories used. These analysis

possibilities only exist if the analytical representation comprises only a handful of

coefficients: the properties of a full series are too general to be useful, except if they

represent known functions or if they are defined by laws of recurrence.

Measurement, Representation and Analysis of Temporal Signals 361

Finally, certain exact solutions of the equations of fluid mechanics, of

thermodynamics and acoustics, can be brought to the solution of linear differential

equations if the partial differential equation is linear, or even non-linear in the most

cases. We have already seen examples (sections 5.4.5.4 and 6.1.1.2.4), which most

of the time correspond to a well-defined physical evolution.

In summary, a curve that is measured or numerically calculated or

a table of n

numerical values gives raw, unstructured information

that is apt to represent many

kinds of signals. On the other hand, an analytical formula, which characterizes the

curve, provides a structured information.

An analytical function with few numerical

coefficients often allows clear physical concepts to be associated with the

information

; obviously this analytical formula can only represent very specific kinds

of phenomena

. The development of computer technology has unfortunately led to

analytical results being neglected, which frequently allow analysis and sometimes

predictions based on physical arguments. Numerical calculations are of course not

to be neglected; on the contrary, it must not be forgotten that they provide

knowledge of the same kind as an experiment.

7.3.3. Signal decomposition on the basis of functions; series and elementary

solutions

7.3.3.1. Representation in the form of a series of functions

Exact mathematical representations can also be obtained in the form of series or

integrals, but in so far as general procedures are concerned, their physical interest is

often limited. Thus, a function of a real variable can be decomposed in terms of a set

of basis functions, of which there are many kinds. For example, a signal can be

represented by a power series development (Taylor) around an instant



)(



This series is often unusable in physics, as the property of infinite

differentiability does not exist; furthermore, the convergence of the series of an

analytical function is often limited to a finite interval. We will nonetheless note the

following particularity of power series developments: all information concerning the

function of time to be represented can be found concentrated at a given instant

This assumes that the future of the function is completely determined from that

instant: the fact of indicating data in the long term creates problems of accuracy

which are manifest in the numerical value of the higher order derivatives. Such a

representation, which is theoretically possible for large values of time (the power

series cos

Zt converges regardless of t), is nonetheless unusable in practice.

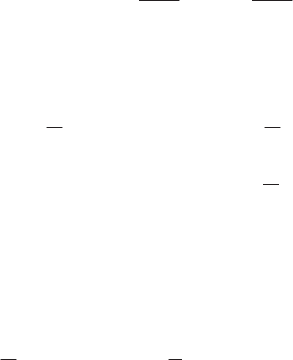
362 Fundamentals of Fluid Mechanics and Transport Phenomena

A function s (t) can also be developed as a Fourier series on a finite interval

[0,

T] of length T:



sin

cos)(

ats

The coefficients

and b

being given by the classical formulae:

   

  

tdTntts

atdts

³³





/2sin.

/2cos.

The Fourier series represents a periodic function of period

T; it is badly adapted

to the representation of very rapid variations and discontinuities.

As the harmonic

functions of period

T/n are orthogonal (where n is an integer), we have:





baadtts

222

This property can be interpreted as a conservation of energy: the energy of the

signal during time

T is equal to the sum of the energies of the harmonics (Parseval’s

theorem).

There exist many other basis functions sets on a finite interval: Bessel functions,

Legendre and Tchehychev polynomials, etc. (see mathematical texts). The interest

in these is often related to the nature of the considered problem. Certain functions

such as real decaying exponentials are particularly useful for the study of damped

systems, but they do not form an orthogonal basis set. Finally, basis functions are

not necessarily continuous, as we will see in a later example (section 8.3.2.3).

7.3.3.2.

Representation by combinations of elementary solutions

The series evoked above are often chosen as a function of simple and universal

mathematical properties (Taylor series, etc.) without any prior consideration of the

physical properties of the system studied. Another manner of constructing solution

representations consists of combining elementary solutions of the equations studied.

For example, for problems associated with Laplace’s equation (electrostatics, steady

conduction of heat or electricity, irrotational fluid flow, etc.), we can seek an

exact

or approximate solution that satisfies the boundary conditions in the form of a

linear combination of monopoles, dipoles and vortices

. In general, such methods are

possible for linear problems in different forms (singularities and multipole