Peube J-L. Fundamentals of fluid mechanics and transport phenomena

Подождите немного. Документ загружается.

Measurement, Representation and Analysis of Temporal Signals 363

distribution methods, Green’s functions, boundary element methods, etc.). These

methods often use a mathematical formalism which can be quite involved and which

we cannot cover in this text.

We will encounter this kind of methodology in the synthesis of musical sounds;

we can however already note that a musical score constitutes a combination of

elementary solutions (the notes of the instruments and indications regarding their

interpretation) which allow the representation of a musical sequence in a manner

equivalent to the numerical values recorded on a CD.

7.3.3.3.

Signal reconstruction

The reconstruction of a signal s(t) represented in the form of a series or as a

combination of functions is an intricate exercise, which can sometimes be quite

difficult. Finding a simple analytical representation of a series is an almost

impossible task, except in very specific cases; only a numerical reconstruction of the

signal is possible.

Let us recall that

a power series is associated with a function independent of the

value of its radius of convergence and it is characterized by the infinite sequence of

coefficients

. Because of this, calculating the value of a function thus represented is a

normal mathematical operation, even if the series diverges. The simplest way to

obtain the values of the developed function

s(t) is to numerically calculate the sum

of the series when possible. In the case of series divergence (or poor convergence),

there exist procedures which allow the divergence problem to be contoured or the

speed of convergence to be improved in order that its sum be efficiently calculated

(analytical prolongation, Euler algorithms, Cesaro or Féjer sums for Fourier series,

etc. The interested reader should refer to mathematical texts ([ABR 65] p. 16, [BRE

91], [PRE 07])).

In summary, a series development of a function

s(t) replaces the function by a

denumerable sequence of numerical values (series coefficients) and knowledge of

the basis functions. However, such developments are only of interest if the function

can be calculated with a small number of terms thus obtained, which is often the

case when the basis functions are solutions of the equations which correspond to the

model of the physical problem (Appendix 4).

7.3.4. Integral transforms

7.3.4.1. Introduction

An integral transform is a generalization of the idea of a series, which amounts

to developing a function on a continuous infinity of basis functions



tg ,

that

depend on the parameter

. Instead of obtaining a denumerable sequence of

364 Fundamentals of Fluid Mechanics and Transport Phenomena

coefficients, the result of the integral transform T of the function s(t) is the function

(

) of the variable

; as the information provided by the function is greater than

that contained in a denumerable sequence of coefficients, we see that the conditions

for applying integral transforms are far broader than those of series developments.

We can often associate an integral transform with a series development. The integral

transforms can comprise complex values.

An integral transform can often be inversed, in other words there exits another

integral transform

–1

whose result T

–1

(T (s(t))) is equal to the original function

s(t). The exact or approximate reconstruction of the initial signal is the obvious

condition for using an integral transform to store a signal. This condition is not

necessary for its analysis.

The

correlation coefficient

of two temporal functions f(t) and g(t) is

defined by the relation:

! 

!!

!

dttgtf

)()(

,:with

In the usual definition, we consider the infinite interval T by taking the limit. In

practice, this coefficient is always calculated on as large a finite interval as possible.

An integral transform is thus a factor excepted no more than the ensemble of

correlations between a function s(t) and the family of basis functions



tg ,

An integral transform only provides interesting information and simplifications

if a large correlation is obtained for a small number of functions



tg ,

. In such

cases significant interpretations may be possible. The use of an integral transform is

only of interest if a reduced set of basis functions represents a notable part of the

properties of the signal studied. There exist many integral transforms. We will give

some examples of commonly used transforms with only some of their basic

properties, chosen on account of their physical interest. The reader will find a more

exhaustive discussion in specialized books ([AND 99], [BEE 03], [DEB 06], [GUP

83], [JER 92], [WOL 79]).

7.3.4.2.

Fourier transforms

7.3.4.2.1.

Definition and properties

We will leave aside the rigorous definition and conditions for existence of the

Fourier transform. Consider a real-valued temporal signal x(t); its Fourier transform

(

) is a complex function of the frequency

defined by the relation:

Measurement, Representation and Analysis of Temporal Signals 365

dtetxF

)()(



f

f

The real and imaginary parts of this transform F

(

) are:

>@ >@

dtttxFdtttxF

QSQQSQ

2sin)()(Im;2cos)()(Re

³³

f

f

f

f



The modulus

)(

F and the phase

)(

F of F

(

), respectively known as

the amplitude spectrum and the phase spectrum, can be written:

>@ >@>@

 

)(Re

)(Im

)()(Im)(Re)(

QMQQQ

xxxx

ArctgFFFF

The temporal signal is reconstructed by the inverse Fourier transform:

deFtx

)()(

f

f

(

) and x(t) are two different and equivalent representations of the same

quantity, respectively in frequency space and in the temporal domain.

The main properties of the Fourier transform are:

1) the property of evenness:

x(t) real  Re[F

(

)] even, Im[F

(

)] uneven

x(t) real even  F

(

) real even

x(t) real odd  F

(

) imaginary odd

x(-t)  F

) = F

(

2) a stretching of the timescale of the function x(t) which leads to a contraction

of the frequency scale for the transform F

(Q) and vice versa (similarity):

)(

)()(

txatx

3) a translation

of the timescale of the function x(t) which leads to a phase

rotation equal to –2S

for the transform F

(Q) and vice versa:

366 Fundamentals of Fluid Mechanics and Transport Phenomena

)()(

)(

QWS

FeF



4) the Dirac distribution

(

) is defined by the relation:

1 ) (

f

dt t

with: 0, ( ) 0

t  tv

It satisfies:



0)()( fdttft

f

f

We can easily show that its Fourier transform is equal to one:

1)()(

)(

f

f



dtetF

The Fourier transform of a Dirac distribution centered at the origin is a constant

function of the variable

, equal to one on the interval [-f, +f];

5) the Dirac distribution

)(

t centered at the instant

verifies:



WWG

fdttft 

f

f

)()(

From the relation of translation of the timescale, we obtain its Fourier transform:

QWSQS

WGQ

jtj

edtetF

)(

)()(



f

f



6) the inverse Fourier transform of the Dirac distribution )( N

in frequency

space is: 

1)((

)()(

)(

221

)(



f

f



f

f



QQG

SQS

deF

edeNtF

tjNtj

7) the Fourier transform of the function

tjN

is then the Dirac distribution

centered on frequency +



)(

)2exp(

tjN



Measurement, Representation and Analysis of Temporal Signals 367

8) the Fourier transforms of the functions

S

2cos

and

S1

2sin

are the half-

sum and the half-difference of two Dirac distributions centered on the frequencies

and -

The function







cos

, continuous in temporal space, is thus

represented by only three numerical values A,

1

and

M

in frequency-space;

9) the Fourier transform of the product of two functions x

(t) and x

(t) is equal

to a convolution product F

(

)*F

(

) of the Fourier transforms F

(

) and F

(

), and vice versa;

10) Parseval’s theorem expresses that the energy of a signal s(t) is conserved by

the Fourier transform:

 

dFdttsE

³³

f

We see completely different distributions of information in temporal and

frequency space: the non-zero temporal signal and the infinite duration of the cosine

function is found concentrated in four non-zero values (frequencies

, amplitude

and phase or complex amplitude), whereas the information of the Dirac

concentrated at the time axis origin is found spread over the entire frequency

domain.

7.3.4.2.2. Interpretation of the Fourier transform

Using the Fourier transform amounts to seeking the correlation between a signal

x(t) and the harmonic signals of frequency

, which can be expressed in the form

S

. This interpretation is valuable because it can be shown that the better this

correlation, the closer the signal is to a harmonic signal. For a signal mainly

comprising harmonic discrete signals, the correlation will be high for corresponding

frequencies (spectrum of lines) and the signal will be characterized by the values of

these lines. We thus obtain a small number of numerical values in the place of the

values obtained by temporal discretization of the signal. The Fourier transform

consists of representing the functions x(t) using a basis-set of harmonic functions.

The application of the Fourier transform on a temporal signal of infinite length

poses two problems that are difficult to reconcile a priori with the idea of

irreversible time associated with the second law of thermodynamics:

– on the one hand, we can only know the transform after a very long period of

time;

– on the other hand, it assumes that the beginning of the signal is situated a long

time ago in the past.

368 Fundamentals of Fluid Mechanics and Transport Phenomena

The first inconvenience makes it difficult to follow the evolution of a

phenomenon without a long enough delay; this can be remedied by means of

observation windows of limited duration. The second difficulty is more serious, as it

implies that the signals obtained by inverse Fourier transform are not possible to

realize if they occupy the time interval [-

, +

]. Only a non-zero temporal signal

which starts from a given instant is realizable: we refer to this as a causal signal,

which defines a possible action in time.

7.3.4.3.

Laplace transform

The Laplace transform possesses properties similar to those of the Fourier

transform, and is defined by the relation:



)()( dttfepL

Laplace transformation is not fundamentally different from Fourier

transformation, as it consists of taking in this Fourier transform imaginary values for

the variable in complex plane; it has the same properties, except for inverse

transformation.

This transform is of considerable interest, notably for the study of damped

systems in automatic control, the family of functions for comparison with the signal

s(t) being precisely the ensemble of aperiodic damped modes of linear invariant

systems of first order. The reader can refer to texts on the dynamics and control of

systems ([BEE 03], [DEB 06], [GUP 83], [WOL 79]). We will see in Chapter 8 the

application of the Laplace transform for the solution of linear systems with constant

coefficients (Appendix 1).

7.3.4.4.

The Hilbert transform

The objective of the Hilbert transform is to define the amplitude and the

instantaneous frequency of a movement which is close to a harmonic movement, by

with variable characteristics. We here have a generalization of the definition of the

complex exponential

ntj

(Appendix 2). We define the Hilbert transform



of the signal



tH by the relation

  

f



uxVPtx

tH .

[7.5]

The notation VP means that the integral has to be understood in terms of Cauchy principal

value; notation

indicates the convolution product of two functions.

Measurement, Representation and Analysis of Temporal Signals 369

The Hilbert transform of

Q

S

cos

is equal to

Q

S

sin

; in general, the effect

of the Hilbert transform is to introduce a phase lag of

2/S

in the initial harmonic

function. For any real signal



tx , we can associate the complex analytical signal







) ( ) ( t



[7.6]

The modulus



ta and the argument



of the analytical signal



can be

defined as the amplitude and the instantaneous phase of the signal x (t):

 



etattx

)(ReRe

The instantaneous frequency

is defined as the derivative of the instantaneous

phase

. The idea of instantaneous frequency is only meaningful for

functions that are close to harmonic functions, in other words for relatively

narrowband signals. We will note that these signals possess two very different

timescales, one rapid timescale corresponding to a “carrier” and another much

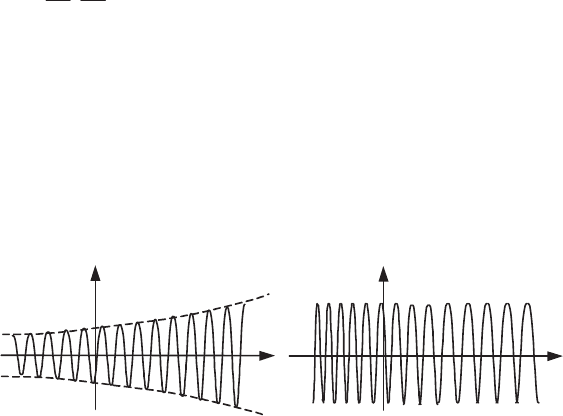
slower scale that characterizes a modulation. Figure 7.8 shows an example of a

signal modulated in amplitude (a) or in frequency (b).

Most musical signals are characterized by a fixed frequency, which is modulated

in amplitude, and in phase. They constitute the basis for the synthesis of sounds in

musical synthesizers. We will come back to this point a little later in section 7.4.3.4.

(t)

x (t)

(a)

(b)

Figure 7.8. Signal modulated in amplitude (a) or in phase (b)

7.3.4.5.

Cepstrum

The principle of cepstrum consists of taking the logarithm of a spectral density,

and then performing an inverse transform. Ordinary products and convolution

products are respectively transformed into sums and products; a harmonic

370 Fundamentals of Fluid Mechanics and Transport Phenomena

modulation of the spectrum is transformed into a Dirac in the inverse transform.

These properties are often used for signal processing applications such as:

– the suppression of echoes in acoustic signals;

– the characterization of vibrations in rotating machinery and more particularly

in obscuring the operation of machines (for example, in looking for defects in

rotating parts which result from the wear of bearings and which leads to the

appearance of lines in the spectrum or by modulation frequencies which are difficult

to see in a simple spectrum).

We will see examples of applications of the cepstrum in Appendix 3. Depending

on the problem, different definitions of the cepstrum are used ([DES 00], [JUR 08],

[NOR 03], [WAI 90]).

7.3.4.6.

Short time Fourier transforms

The Fourier transform is defined on an infinite interval. For diverse reasons, we

can only record a signal over a limited duration, and this modifies the Fourier

transform. It is thus necessary to find a compromise between the volume of

information required and the accuracy of the results obtained. Recording a signal for

a finite duration

, consists of multiplying it by a non-zero function over this

interval and by zero outside of this interval. Following the usual terminology, we

will say that this function, called a gate function

(t), is a particular case

(rectangular function) of a window function. The gate function

(t) centered at the

origin can be written:













tTTt

TtT

220

22 1

) (

The signal transform thus truncated is written:

)(*)()()( ) (

dtet



f



3

The Fourier transform of the truncated signal

(

3

(

) is equal to the

convolution product of the Fourier transforms of the signal

(

) on the infinite

interval and the gate



(t). The Fourier transform

)(

of this one is a cardinal

sine function:

sin

)(

Now consider the effect of recording the signal

2cos using a gate of

duration

. The Fourier transform of a cosine of infinite duration is composed of

Measurement, Representation and Analysis of Temporal Signals 371

two Diracs (Figure 7.9a): the spectrum of the cosine convolved with the transform

of the gate of duration T is comprised of two cardinal

sinusoids centered on the

frequencies

of the two preceding Dirac distributions (Figure 7.9b). Considering

that the width of the central peak of the cardinal sinusoid is characterized by its first

zero, the widening of the Dirac function peak is equal to 2/

, which is, for a

window

which records 10 periods

, a widening in frequency of 0.1

on either side of the

frequency

+ n - n

(a)

+ n- n

2 /T

(b)

(c)

+ n- n

T

Figure 7.9. Fourier transform of: (a)

cos 2 ; nt

(b)

ntt

2cos ).(

3

with

1/T << 2n; (c)

ntt

2cos ).(

3

with 1/T = 2n



We see that the shorter the window, the wider the frequency band obtained: an

insufficient observation will reduce the accuracy of the Fourier transform by

“clouding” the signal.

We note that as a recording which does not disturb the

spectrum should be applied with a window which is the inverse transform of the

Dirac distribution, in other words the unrealizable infinite width time window,

which we wanted to avoid.

According to the usual Rayleigh criterion, we consider that the frequency peaks

become unidentifiable if the first zero of the cardinal sinusoid centered at the

frequency +

n is found at the frequency –n (Figure 7.9c), i.e.:

nT 2/1

The perception of a frequency

n requires thus an observation horizon of duration

T greater than 1/2n: the recording duration T should include at least a half period of

the lowest visible frequency of the short-time Fourier transform. Another result of

these considerations is that we can only distinguish two frequencies

Q

and

Q

they are separated by at least the value 1/2

T. From a physical point of view, an

insufficient recording of information can only give bad results (see formula [7.8]

and Shannon’s sampling theorem (section 7.3.6.4)). We will note that the spectrum

obtained by such a transform has not only lost the details concerning the peak; but it

also contains low frequencies that do not exist physically.

We obtain:

  

tfdtf



f

WWGW

372 Fundamentals of Fluid Mechanics and Transport Phenomena

The Fourier transform is thus only a correlation performed between a signal and

a family of harmonic reference signals. This observation allows a simple physical

interpretation of the widening of peaks, which results from the use of a finite

window. In effect, the correlation between two harmonic functions is zero over an

infinite time, unless their frequencies are equal. However, the same correlation will

be increased, as the window size become progressively smaller and as the

frequencies are nearer. We will leave it to the reader to verify these observations.

In reality, the widening of the Dirac spectrum by the cardinal sinusoid function

is not limited to the central peak of this function and the smaller but non-negligible

amplitudes of the lateral lobes can also lead to a net increase in the width of the

spectrum obtained. This last inconvenience is a problem, in particular for analyses

of acoustic signals on account of the sensitivity of the ear (the logarithmic decibel

scale clearly leads to a smaller scale of the amplitude variations). As the energy of

the secondary lobes is quite weak, we try to re-center it on the main lobe, even if

this means widening it slightly. This can be achieved by replacing the gate function

(t) by a window function )(t

)

, which leads to much smaller amplitudes of the

lateral spectrum peaks than those obtained with a rectangular window:

)(*)()()()(

QQQ

FFdtetxtF

)



f

f

)

[7.7]

The recording of a raw signal over a limited duration therefore leads to

deformations of the Fourier transform consisting of two kinds of distributive

modification of spectral energy: the widening of the central peak and the appearance

of secondary lobes. This widening of the signal spectrum can be studied and

characterized for each window by taking the “moment of the signal energy”

dttxt

)(

and of its transform

QQQ

)(

. General considerations ([BLA

98], [FLA 98], [HIG 93], [STR 96]) allow the demonstration of the Heisenberg-

Gabor inequality:

tQ''

[7.8]

In this inequality 't and '

are respectively the duration of the energy content of

the temporal signal and the width of the frequency band in which the energy is

contained; 't is of the order of T/2 and '

is analogous to the quantity 2/T defined

above for the rectangular gate. The equality is obtained for a Gauss window, which

corresponds thus to an optimum of the preceding minimization criterion. The

limitation of the preceding principle is related to the basic uncertainty of quantum

mechanics, but the physical analogy is far from complete, the interpretation of

quantities being very different in the two domains.