Peube J-L. Fundamentals of fluid mechanics and transport phenomena

Подождите немного. Документ загружается.

Transport and Propagation 223

which can be easily interpreted by taking a reference frame for which velocity (u, v)

of a point M is zero at time t (this reference frame has the speed of the matter of

point M at the considered instant). In this last frame the previous substantial

derivative

[

is equal to

[

, so that the previous equation relation

between derivatives of function

[

is written:



),(



tMtM

yxt

tMc

[[[

showing that the vector

tMtM

yxt

[[[

is located on the revolving

cone of summit M, of axis Ot and whose equation is:

  

),(

222



MMM

yyxxtt

tMc

The tangent planes at point M to the characteristic surfaces are normal to the

vector

tMtM

yxt

[[[

, which makes an angle ]),(1tan[ tMcArc

with the axis Ot. They envelope the complementary cone of revolution whose angle

with axis Ot is equal to tan[ ( , )]

Arc c M t and whose equation is:

  

0),(

222



MMM

yyxxtttMc

The characteristic curves comprised by the cone satisfy the relations

222

 dtcdr

which describe radial propagation at the speed of sound c with

respect to the matter.

5.3.6. Physical interpretation of propagation

The partial differential equations of fluid dynamics and transfer are balance

equations; we have now outlined the essential ideas which govern the manner in

which material quantities are displaced on the characteristic curves either by

convection (transport of material quantities by fluid particles) or by propagation.

224 Fundamentals of Fluid Mechanics and Transport Phenomena

The latter mode results from the exchange of extensive quantities between fluid

particles, from one to the next and so on. It can be simply interpreted.

Consider a string of coupled oscillators comprising the masses m and springs of

stiffness k and length

'x. Let x

be the coordinate where the n

mass is at rest, and

let

[

be its displacement with respect to this rest position (Figure 5.3).

n-1

n+1

[

n-1

[

n+1

Figure 5.3. Propagation on a line of mass-spring oscillators

The equation of motion for the n

mass can be written:





 nnnn

[[[[



[5.40]

Consider this string to be a model for a continuous medium with spatial

discretization

xxxxx

nnnn

'  



...

The second spatial derivative can be approximated by:

nnn





[[[

[

such that by letting

mkxc '

, equation [5.40] becomes a wave equation:



xtc

[[

The

propagation of waves results from interactions between the mass of the

medium and its compressibility

(or what is equivalent, its elasticity). In the

continuous compressible medium, the mass and the elasticity are uniformly

distributed.

The reader can verify that stiffness per unit length is

k'x

and mass per unit length is m/

so that by identifying the mass and the stiffness with corresponding properties of gas pressure

and specific mass), we obtain the value of the sound velocity





Transport and Propagation 225

5.4. Second order partial differential equations

5.4.1. Introduction

We have just shown that a system which flows generally presents at least one

family of characteristic curves (its trajectories) which correspond to the transport of

matter and on which there exists a balance relation for the extensive quantities

(entropy, mechanical energy, etc.). In many practical cases, the flowing fluid may

possess properties of homogenity, either dynamic (absence of vorticity) or physical

(constant entropy). If we have strict conservation of this quantity everywhere in the

flow, then the corresponding partial differential equation can be immediately

integrated. For example the steady 1D flow studied in section 5.3.2.1 is

homoentropic, which leads to the existence of the relation



We can thus often obtain a quasi-linear second order partial differential equation

(i.e. linear with respect to the second derivatives) for one of the quantities of the

problem by using a system of first order partial differential equations.

For example, let us assume for the sake of simplicity that the density and

velocity variations are small enough for the linearization of equations [5.13] to be

possible in a constant entropy medium:

0;0



Using the definition of the speed of sound



, here assumed to be

constant on account of the linearization, we obtain the wave equation:



We will now reconsider quasi-linear second order partial differential equations

with two variables, in a form largely used in practice when a velocity potential exists

(the homentropic flow of a compressible fluid, waves on the surface of liquids, etc.;

see Chapter 6). Furthermore, as their characteristic equation is of second degree, it is

locally of a well-defined type, elliptic or hyperbolic depending on whether the roots

are imaginary or real. This facilitates a discussion of a problem’s boundary

conditions.

Consider the quasi-linear second order partial differential equation with two

variables:

DtCsBrA  2

[5.41]

226 Fundamentals of Fluid Mechanics and Transport Phenomena

with the usual notation:

tfsfrfqfpf

yyxyxxyx

The coefficients

A, B, C

and

are functions of the unknown function

and of its

first derivatives

and



.,,,,;,,,,

;,,,,;,,,,

yxqpfDDyxqpfCC

yxqpfBByxqpfAA

5.4.2. Characteristic curves of hyperbolic equations

Because of the practical applications of this formulation, we will reconsider the

Cauchy problem, which consists here of determining the solution using data for

and its derivatives (

p,q

) on a curve

in the plane (

x,y

). In order to know the

function

at all points in the neighborhood of the point (

x,y

) in

, it suffices to

know the second derivatives (

) at that point (we can then calculate the higher

order derivatives in a similar fashion by successive differentiations of equation

[5.41]). The functions (

) satisfy the relations:

qytxspysxrDCtBsAr

   ;;2

[5.42]

or, in matrix form:

CBA

[5.43]

As a function of the known variations



, of



, on the curve

between the points



yyxx



and

(x, y) on this one

, we can generally

calculate the quantities



tsr

,, at (

), except if the characteristic determinant of

system [5.43] is zero:

00or: 2 0

ABC

 x  yC xB x yA y

 x  y



[5.44]

4 In order to simplify the writing in section 4.6 and in any other case when it will be useful,

partial derivatives

will be written

, a notation that does not allow any mistake

in mathematical calculations.

Transport and Propagation 227

The directions

ACBB

r

, solutions of the preceding equation, are

the

characteristic directions

tangent at each point to the characteristic curves:

– if 0

! ACB

the roots of the characteristic equation are real and the

equation is of a

hyperbolic

kind;

– if

 ACB

the roots of the characteristic equation are imaginary and the

equation is of an

elliptic

kind; the Cauchy problem always possesses a unique

solution in the neighborhood of any curve on which the values of the functions (

) are given;

– if 0

 ACB

the characteristic equation possesses a double root, and the

equation is of a

parabolic

kind.

In the hyperbolic case, the determination of (

), which is non-unique on the

characteristic curves, is only possible if the system of equations [5.42] is of rank 2.

There then exists a relation between

G

and

G

which can be obtained, as

outlined in the preceding sections, by searching for a vector

which is a left

solution of the system 0

, where

is the system matrix [5.43] without the

right-hand side. We find:



xCyAyxL



By multiplying the left-hand side of system [5.43] by

we obtain the following

relation for each of the solutions



of characteristic equation [5.44]:

.2,10



iiii

[5.45]

Relations [5.45] allow the function

and its derivatives (

) to be calculated

from place to place in the following manner. Consider the subdivision ABDEF of an

arc of the curve

and trace at each of the points the two families of characteristics

and

of slope



, (

=1, 2). The different families of characteristics

obtained from A and B intersect at G (Figure 5.4). We obtain relation [5.45] on each

of the arcs AG and BG, which allows the values of

and

to be calculated as a

function of their values on the curve

at A and B. Assuming the arcs to be

sufficiently small, these relationships can be written:

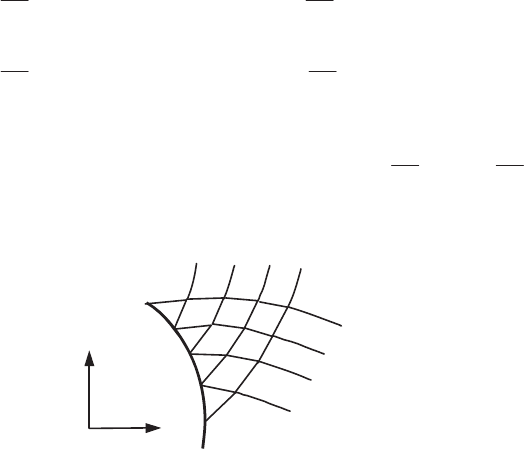
228 Fundamentals of Fluid Mechanics and Transport Phenomena

 









BGBGBG

AGAGAG

AqqCxx

the elementary arcs AG and BG having respective slopes

and

Characteristics *

(a)

Figure 5.4.

Domain of influence of the arc AF of the initial curve C

The preceding relations uniquely determine p

and q

as a function of the values

of f, p and q at A and B. We thus see that the initial values on the curve C

propagate partially on each of the characteristics by virtue of relation [5.45]. The

value of f at G is determined by the mean of the finite variations formula between

the points A (or B) and G:



AGAAGAAG

yyqxxpfff  

The values f, p and q of the solution of the partial differential equation can thus

be determined from place to place by the preceding procedure at any point within

the curvilinear triangle AFM, which is delimited by the arc AF and the arcs AM and

FM of the characteristic curves: in effect, it suffices for this point to be attained by

progressing along the two families of characteristic curves starting from the initial

arc AF. The inner domain of the curvilinear triangle AFM is called the influence

domain of the arc AF of the initial curve C

This method is not applicable to parabolic equations: by considering the case B

= C = 0 in equation [5.41], relation [5.44] gives

y= 0, and system [5.45] gives no

Transport and Propagation 229

new relation on the characteristic curves comprising the axis Ox. We will return to

discuss the parabolic equation in section 5.4.5.4.

In summary, the solution of the Cauchy problem is always possible for an elliptic

equation regardless of the choice of initial data. On the other hand, the existence of

real characteristic curves or surfaces implies a propagation of function values along

these curves.

5.4.3. Reduced form of the second order quasi-linear partial differential equation

We will demonstrate that a second order quasi-linear partial differential equation

can be locally changed, at all points, to a standard reduced form.

Recall firstly that a quadratic form

2 CnBmnAm 

can be written in a

reduced form by means of an appropriate change of basis. In effect, by considering

the new variables (

fendcm  

the preceding quadratic form can be written as a function of these:

2222

JQEPQDP

  CnBmnAm [5.46]

By appropriately choosing the coefficients (c, d, e, f) of basis change, we can

eliminate

and make equal the absolute values of

and

. Let us apply this

procedure to equation [5.41], which can be associated with the quadratic form

2 CnBmnAm  whose coefficients are functions of the quantities (f, p, q, x,

y).

The change of coordinates

 

yxfFyxyx ,,),(),(

[

transforms equation [5.41] into another equation of the same kind. Showing

explicitly only those terms containing second order partial derivatives, we have:



.....2

.....

...2

;







 

yyyyyy

yxxyyxyxxy

xxxxxx

yxyxxx

FFFf

FFfFFf

\\MM

\\\M\MMM

\\MM

KK[K[[

K[K[

230 Fundamentals of Fluid Mechanics and Transport Phenomena

The left-hand side of equation [5.41] can be written:



2 2 ....

with:

xx xy yy   

xx y yx y

xxyy

Af Bf Cf  F  F  F

!A# B#!B# C#

 A! B!! C!

 A# B## C#





 

[5.47]

We can immediately verify the relation:







xyyx

BAC

\M\MEDJ

 

which shows that the discriminant of the quadratic form retains the same sign after

the coordinates change.

The reduction to the normal form can be obtained by letting

D

J

and

= 0.

This last condition is satisfied by letting:









yxyyxx

BAMCBM

\\M\\M

  ..

[5.48]

By replacing in [5.47] the derivatives of

with the preceding expressions, we

can show that the coefficient

can be written:













J\\\\D

222222

2 BACMCBABACM

yyxx

  [5.49]

Depending on the value of

BAC  , we can distinguish the following cases:

– Elliptic case:

! BAC

Letting





 BACM , we have

. The characteristic equation

[5.44] does not have a real solution and equation [5.41] is elliptic; as the coefficient

is non-zero, the second derivatives can be regrouped in the form of a Laplacian:





DFFCfBfAftCsBrA

yyxyxx

   ....22

KK[[

– Hyperbolic case:



BAC

Letting





  BACM , we have

 . The reduced form of the

equation [5.41] can be written in the form of a wave equation:





DFFCfBfAftCsBrA

yyxyxx

   ....22

KK[[

Transport and Propagation 231

Another reduced form of the hyperbolic equation can be obtained by

alternatively choosing the functions

M

and

to represent the two families of

characteristic curves ( , ) constxy

[

and ( , ) const; xy

in the place of

relations [5.48], we let the tangent slopes of these curves equal the roots of

characteristic equation [5.44] (the characteristic curves are taken as local coordinate

curves):



;

It now follows from equation [5.44]:

022

2222

 

yyxxxyxy

CBAABC

\\\\MMMMJD

By substituting the product and the sum of the ratios

and

their expressions obtained from the characteristic equation [5.44], we obtain the

non-zero coefficient

defined by [5.47]:



 

CCBA

yyyyxyyxxx

\M\M\M\M\ME

Equation [5.41], now considering the characteristic curves, can be written:

'DF

where D' is a function of coordinates, and of the values of F, and of its first

derivatives.

–Parabolic case:



BAC

We take

such that



to obtain D = 0; it follows that

= 0; and

the normal form of the parabolic equation is then:

...



FD

We will return to the properties of the parabolic equation when we consider it in

terms of constant coefficients (section 5.4.5.4).

NOTE – As pointed out (section 5.4.1), we have verified that second order partial

differential equations no longer have characteristic curves which represent

trajectories, even though they do represent flows.

232 Fundamentals of Fluid Mechanics and Transport Phenomena

5.4.4. Second order partial differential equations in a finite domain

5.4.4.1. The significance of the Cauchy problem

In systems of quasi-linear partial differential equations, we can have mixed

situations: for example, the flow of the incompressible fluid discussed in section

5.3.2.2 only represents a single family of characteristic curves, on which only

mechanical energy is transported, but no other quantity propagates. On the other

hand, the quasi-linear second order partial differential equations lead to two

principal kinds of local situation:

– second order elliptic equations always possess a solution to the Cauchy

problem, which implies that the initial data have a significant influence on the

solution in their neighborhood;

– hyperbolic equations lead to a double structure associated with two families of

characteristic curves on which the initial information is transmitted.

While elliptic equations distribute information in all directions, hyperbolic

equations transmit it along the “fibers” of two bundles of curves. However, as the

elliptic or hyperbolic character is a local property, an equation can be hyperbolic in

one region of space and elliptic in another.

Our discussion of the Cauchy problem shows us that the simultaneous presence

in a flow of subsonic and supersonic zones leads to very different modes of

transmitting information and to certain contradictions; this results in important

difficulties regarding the boundary conditions which must be imposed, which are

different in the two cases (section 5.4.5). This situation often leads to the presence of

shock waves. We will consider a simple example by studying the flow of a

compressible fluid in a nozzle (section 5.5.4).

The understanding of these situations and of these properties is particularly

important, not only for the discussion of physical phenomena, but also for numerical

calculations whose algorithms must be chosen such that numerical information is

transmitted in a manner which is compatible with the general properties which we

have just outlined.

5.4.4.2.

Constant coefficient second order partial differential equations

When the coefficients A, B and C are constants, the nature of the partial

differential equation is identical in all parts of the domain studied.

Constant coefficients elliptic equations with no right-hand side can be expressed

as a Laplace equation: