Peube J-L. Fundamentals of fluid mechanics and transport phenomena

Подождите немного. Документ загружается.

Transport and Propagation 203

5.2. First order quasi-linear partial differential equations

5.2.1. Introduction

In expressing the laws of physics in a local form, we obtain partial differential

equations, the functions representing the physical quantities depending on space and

time variables. These equations have properties which are quite different from

differential equations, because their general solution no longer comprises a family of

functions with a finite number of parameters, but a family of functions which we can

choose arbitrarily. Let us take the simple example of the equation:

whose solution depends on the two arbitrary functions

and

\

)()(),( yxyxf



This solution is only a general form of the function dependence with respect to

the variables. The choice of these functions will depend on the boundary conditions

which are specified.

As with the differential equation, we can define a Cauchy problem: for example,

for a partial differential equation with two variables



yx, , the unknown function f

is given on the curve C

of the plane (x,y) and we seek to evaluate this function in

the vicinity of C

In what follows, we will limit ourselves to a relatively elementary approach

which only consists in verifying the existence of a series expansion in the place of a

solution. We thus identify the essential properties of the solutions and the basic

concepts which govern the general physics of the phenomena studied.

We will not demonstrate the uniqueness of the solution, as this requires advanced

mathematical knowledge and precise assumptions which do not necessarily have

physical reality, for example:

– do analytical functions (indefinitely differentiable) exist?;

– what is the nature of the “relation” between distributions and physical

problems?;

– how can we verify the physical reality of a Lipschitz application (section

1.1.1.4)?

204 Fundamentals of Fluid Mechanics and Transport Phenomena

DEFINITION – A quasi-linear partial differential equation is an equation which is

linear with respect to the partial derivatives of highest order, whose coefficients are

functions of variables and derivatives of lower order.

The equations which we will encounter in mechanics and energy of continuous

media will be quasi-linear.

5.2.2. Geometric interpretation of the solutions

We have previously seen that the substantial derivative in the equations of fluid

mechanics describes transport of a quantity associated with matter. We will recover

this interpretation of the substantial derivative by purely mathematical

considerations.

Consider the partial differential equation which represents transport of the

quantity F, in which the right-hand side is equal to g(f,x,y,t):

),,,( tyxfg



[5.3]

The coefficients u and v are given functions of (f, x, y, t). Equation [5.3]

describes the balance of the scalar quantity F (mass, entropy, number of moles of a

chemical species, etc.) associated with the corresponding specific quantity f (section

4.2.1.2.1). The function g can be considered a source of quantity F, as it only

depends on the coordinates of the material particle and the associated value of the

function f. There is however no interaction with the neighboring particles, and

equation [5.3] does not contain any diffusive flux term for the quantity F. Balance

equation [4.3] of the volume quantity

f can thus be expressed in the form [5.3].

Let us ignore for the moment the physical interpretation of equation [5.3], of

which we will here give a geometric interpretation. In the 4D space (

t, x, y, z),

consider the surface

S described by the equation:



0,,),,,(  ) tyxfzzyxt

We know that the vector

)grad of components





1,,,

yxt

fff 

is normal to

S. The equation of the plane tangent to the surface S at the point (t, x, y, z) can be

written (designating the usual coordinates (T, X, Y, Z)):

Transport and Propagation 205

 

0 



 zZyY

[5.4]

Comparing equations [5.3] and [5.4] shows that the vector (1, u, v, g) is located

in the plane tangent to the surface S. The solutions to the partial differential

equation are thus represented by surfaces tangential to the vector field



gvu ,,,1 in

the said 4D space. Now the curves tangent to the vector field (1, u, v, g) can be

obtained by integration of the system of three differential equations:

[5.5]

The curves defined by system [5.5] are called characteristic curves. We note

immediately that the first two differential equations define the trajectories of fluid

particles (section 3.3.2). The third differential equation allows the unknown function

f to be calculated on these curves. We thus obtain a Lagrangian (substantial)

representation of the balance of the quantity f associated with the fluid particles.

(a) (b)

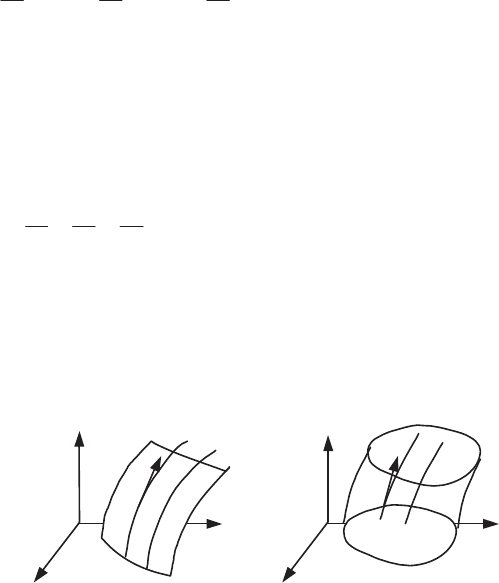
Figure 5.1. C: characteristic curve; S: solution surface;

: surface with initial conditions (Cauchy problem)

Note that the solution of equation [5.3] amounted to the solution of a system of

differential equations with initial conditions. In the preceding 4D space, any surface

S constituted of characteristic curves (characteristic surface) is tangent to the vector

field V

(1, u, v, g); it is thus a solution of the partial differential equation (Figure

5.1a). If a trajectory point C belongs to a surface S, then the curve C lies entirely on

In summary, any quasi-linear first order partial differential equation can be

interpreted as a transport equation for a quantity on the trajectories associated with

that equation.

206 Fundamentals of Fluid Mechanics and Transport Phenomena

This property allows the definition of the ideas of input (the surface S

on which

the initial conditions are given) and output (any surface derived from S

“translation” following the characteristic curves). This introduces a dissymmetry

between the input and output. Depending on the physical context of a problem, the

ideas of input and output may correspond to upstream and downstream, or to initial

and final conditions.

5.2.3. Comments

1) The preceding reasoning can be applied to any number of variables.

2) The preceding mathematical interpretation actually amounts to writing the

balance of the quantity F in Lagrangian variables. For any material particle M

which is displaced on this solution surface S of the 4D space, the associated volume

quantity satisfies:

., :w0 vdtdyudtdxithdfdy





[5.6]

The balance equation

for each fluid particle describes the compatibility

between relation [5.6] and partial differential equation [5.3]. The preceding

considerations show the

equivalence between the Lagrangian balance formulation

in the form of differential equations

[5.5], and

the balance equation in Eulerian

variables, expressed in the form of partial differential equation

[5.3].

3) In the

presence of diffusion of the quantity

, the right-hand side of the

balance equations is not of the form



tyxfg

,,, , rather it contains the second order

transverse derivatives with respect to the characteristic curves: these derivatives

express an interaction between neighboring characteristic curves due to diffusion of

the quantity

. The introduction of higher order partial derivatives modifies the

properties found earlier. However, these partial derivatives are associated with a

coefficient which is often very small, and which leads to a reduction in the order of

the equation, except in singular zones (sections 6.4.3 and 6.5.3): nearly everywhere,

F is transported on the trajectories, with the source

taken into account.

5.2.4. The Cauchy problem for partial differential equations

We will reconsider the preceding problem in the mathematical form, which

consists of solving the Cauchy problem where the value of the unknown function is

given on the surface

, and where we seek to calculate its value in the

neighborhood of

by means of the partial differential equation. This problem can

Transport and Propagation 207

be solved by means of geometric interpretation (Figure 5.1b), provided that the

surface

does not comprise characteristic curves (characteristic surface).

In effect, we have seen that the calculation of the function

can be performed by

integration over the characteristic curves (trajectories): in order for this calculation

to be possible, these characteristic curves must obviously cross the surface

which the initial values of the function

are given.

Note that the solution of equation [5.3] is only defined in the domain

of the

space containing the characteristic curves which cross the surface

is the

influence domain of the initial conditions given

. It is rigorously delimited.

This property is specific to all quasi-linear first order partial differential equations.

In summary, the Cauchy problem for a first order partial differential equation

was reduced to an ensemble of independent Cauchy problems for a system of

ordinary differential equations on each of the characteristic curves (trajectories). In a

transverse direction with respect to these curves, the partial differential equation

gives no information regarding the function

the solution on characteristic curve C

has no influence on its neighboring points

, except on

. The properties of the

solution in the neighborhood of a characteristic curve are uniquely fixed by the

initial conditions corresponding to this neighborhood. The solution space is thus

found to be as a bundle of fibers.

We will later return to the Cauchy problem (section 5.3.5.1) in a more local

manner, and one which is closer to the practical methods used for numerical

calculations.

5.3. Systems of first order partial differential equations

5.3.1. The Cauchy problem for n unknowns and two variables

Consider now a quasi-linear system of first order partial differential equations

with

unknown functions and which we will here limit to two independent variables

(

x,t

). The simplest equations of fluid mechanics involve at least three

thermodynamic quantities (for example, the density

, a velocity component

and

the pressure

) which we will represent by the vector

with three components



321

fff

. Consider the system of three equations described in vector form (the

case of

unknown functions can be treated in an identical manner):

208 Fundamentals of Fluid Mechanics and Transport Phenomena

[5.7]

We will adopt the position of the Cauchy problem: we assume that the value of

is known on a curve

of equation



in the plane (

x,t

), and that from a

point (

) of this curve, we seek to calculate the value of the function

in its

neighborhood: this is possible if we know the value of the partial derivatives

and

at the point (

). The calculation of these is possible using data on the

curve

and equation [5.7]. Designating the elemental arc



, of the curve

and the growth

on this arc, we have:

GGG



[5.8]

Eliminating

between [5.7] and [5.8] we have the system:



[5.9]

If the determinant

 of the system [5.9] is non-zero, the unknown

has a unique value. We can therefore obtain the value of F in the neighborhood

of the considered point and the Cauchy problem has a unique solution. The

preceding determinant is called the

characteristic determinant of system [5.7]. Its

value depends on the ratio

tx , in other words on the choice of the curve

Suppose now that the determinant

Q of the system [5.9] is zero, tx

is a

root of characteristic equation [5.10]:

0  A

[5.10]

Transport and Propagation 209

The corresponding curve C

is the characteristic curve associated with the root

. When all the roots of the equation 0 Q are real, system [5.7] is called

hyperbolic (or totally hyperbolic).

When the characteristic determinant is zero, the system rank [5.9] has diminished

by one unit and a non-zero solution exists for system [5.9], if we have a

compatibility relation between the components of the vector

 of the

right-hand side.

This relationship can be obtained, for example, from the non-zero left solutions L

(eigenfunctions) of the characteristic equation:



0  ABL

[5.11]

Multiplying on the left side [5.9] by L and taking account of [5.11], we then

obtain the relationship sought between the components of

G

F on the characteristic

curve concerned:



AGL

[5.12]

In summary, characteristic curves of the plane (x,t), on which the characteristic

determinant cancels out, are such that:

– the given values of F do not allow the Cauchy problem to be solved

(calculation of F in their neighborhood);

– the unknown vector function F satisfies particular differential relations.

As in the case of solutions to quasi-linear partial differential equations, the last

property can be used to study the solutions. We will come back to this point a little

later.

NOTE – The relationship between the components of

G

F is of “Lagrangian” type in

the sense that the value of this variation is calculated for corresponding values of

G

and of tdx

: the evaluation point of

F is displaced at “velocity”

We will examine two particular cases which show the physical interest of these

results.

210 Fundamentals of Fluid Mechanics and Transport Phenomena

5.3.2. Applications in fluid mechanics

5.3.2.1. Unsteady 1D flow of a compressible inviscid fluid

The equations of a compressible perfect fluid in unsteady inviscid flow can be

written ([4.6], [4.22] and [4.55]):



[5.13]

Letting:

;

;;

BIA

, they can be written

in vector form [5.7]:



Equation [5.9] can thus be written:



 )( [5.14]

We can thus derive characteristic equation [5.10]:

  





cucuu

OOO

[5.15]

The three roots



ucu r, of equation [5.15] correspond, respectively, to a

displacement of the fluid matter on the trajectory



tux

, and to propagation

at the speed of sound c with respect to the matter which moves with velocity u



tucx

r .

Transport and Propagation 211

The system for the left eigenfunctions



321

LLLL of [5.11] can here be

written:







321







uLL

cLuLL

IBL

UOU

[5.16]

The vector L corresponding to each of the eigenvalues can be easily calculated.

Relation [5.12], which provides the relation between the variations

G

F of the

components of the vector F, can thus be written:

0. FL

[5.17]

1) For the root

= u, we obtain:





cL  and:



010



UGG

ucFL [5.18]

Here we recover the relationship which characterizes isentropic transformations

(formula [1.27]): the entropy remains constant during matter displacement. The

reader should note that the identification of this simple property required some

mathematical developments.

2) For the eigenfunctions uc r

solution of system [5.16] gives:



12 3

0i.e. 0 1

LB  IL Lc L cL c

L  Lc

¬















   o















®

We thus obtain:



010

ucp

GUG

[5.19]

These relationships correspond to acoustic waves which propagate in two

directions at the speed of sound

with respect to the fluid matter which moves with

velocity

212 Fundamentals of Fluid Mechanics and Transport Phenomena

NOTES –

1) Relation [5.16] for each of the roots

O

can be written

in Lagrangian variables

By means of linear combinations using initial system [5.13] of the equations of

motion describing the flow of a compressible perfect fluid, we can easily obtain the

system of equations:



ttD

tDt

tdt















:with0

[5.20]

This system is the expression in Eulerian variables of relations [5.18] and [5.19].

We furthermore obtain the directions of characteristic curves from the preceding

expression of derivatives in relations [5.20] [YIH 77, p.211].

2) The case of an incompressible fluid

ww xu

can be obtained by letting the

speed of sound tend to infinity. The eigenvalues of the acoustic propagation

disappear, and only the eigenvalue

utx

exists with the characteristic variable

. The reader can verify that this result can be obtained from [5.13].

5.3.2.2.

Steady 2D flow of an incompressible perfect fluid

The equations for this kind of flow can be written ([4.6] and [4.22]):

0;0;0



UUUU

[5.21]

and can be put in the form [5.7] (



) with:

;

010

;;

001

[5.22]

Following the steps outlined in section 5.3.1 leads to the vector equation: