Peube J-L. Fundamentals of fluid mechanics and transport phenomena
Подождите немного. Документ загружается.


Fluid Dynamics Equations 163
This gives:
W
U
divUgradsgradThgradVVrot
V
grad
t
V
1
2
2
w
w
G
G
[4.18]
or:
W
U
divsgradTVVrothU
V
grad
t
V 1
2
2
¸
¸
¹
·
¨
¨
©
§
w
w
G
G
[4.19]
We note that despite the presence of enthalpy and entropy in equation [4.19], the
origin of this equation is purely mechanical (we have so far not considered any
energy balance).
4.3.1.3.
The case of a Newtonian fluid
The term
W
div , which represents the viscous stresses, can be expressed using
one of the forms discussed in section 3.4.3.3:
»
»
¼
º
«
«
¬
ª
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
»
»
¼
º
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
k
k
ii
j
j
i
jj
ij
x
u
xx
u
x
u
xx
PKP
W
3
2
In the case where the viscosity coefficients are constant, we have expression
[3.58] and the Navier-Stokes equation is written as:
VdivgradVrotrotUgradpgrad
dt
Vd
G
G
¸
¸
¹
·
¨
¨
©
§
3
2
P
KPUU
[4.20]
The expansion velocity is usually small and we have, from [3.60]:
jj
i
ii
i
xx
u
x
U
x
p
dt
du
ww
w
w
w
w
w
2
PUU
[4.21]
4.3.1.4.
Inviscid fluids – the Euler equations
When viscous terms are negligible in [4.21], we obtain Euler equations:
¸
¸
¹
·
¨
¨
©
§
w
w
fpgrad
dt
Vd
f
x
p
dt
du
i
i
i
G
G
UUUU
;
[4.22]
164 Fundamentals of Fluid Mechanics and Transport Phenomena
For a compressible fluid, we can express the pressure as a function of enthalpy
and entropy ([4.17]):
2
(gravity: )
2
VV
grad U h rotV V T grad s U g z
t
¬
s
s
®
G
JJJJJG JJJGJJG JJJJJG
G
[4.23]
Assuming a compressible inviscid fluid we have a situation where the fluid
particles undergo isentropic transformations.
If the flow is homoentropic (s is constant in all the fluid), we have:
2
(gravity: )
2
VV
grad U h rotV V U gz
t
¬
s
s
®
G
JJJJJG JJJGJJG
G
[4.24]
Note the presence of the rotation vector
Z
G
(or vorticity
Z
G
G
2
Vrot
) on the
right-hand side of the preceding equations; we will consider the consequences later.
If the fluid flow has constant and uniform density, the Euler equations can be
written with the driving pressure
gzpp
g
U
:
¸
¸
¹
·
¨
¨
©
§
w
w
g
i
g
i
pgrad
dt
Vd
x
p
dt
du
G
UU
[4.25]
This form of dynamic equation shows that the cause of movement (local result of
external forces) is indeed the driving pressure gradient.
4.3.2. Kinetic energy theorem
4.3.2.1. Local equation
The kinetic energy theorem is a consequence of the Navier-Stokes equations; the
local form of the kinetic energy equation is obtained as before (section 3.2.2.1) by
taking the scalar product of dynamic equations [4.13] and the velocity vector:
j
ij
iii
i
i
x
uuf
V
dt
d
dt
du
u
w
w
¸
¸
¹
·
¨
¨
©
§
V
UUU
2
2
[4.26]
Kinetic energy is not an extensive quantity for which a conservation principle
applies; we can nevertheless consider [4.26] as a balance equation (section 3.2.4.3).
Fluid Dynamics Equations 165
Replacing the stress tensor with expression [3.39] and assuming that the external
force f
i
derives from a potential U, we obtain, after grouping similar terms:
j
ij
i
i
i
i
i
x
u
x
U
u
x
p
u
V
dt
d
w
w
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
W
UU
2
2
or:
j
ij
i
i
i
i
i
x
u
x
p
uU
V
x
u
V
t w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
W
UU
22
22
[4.27]
4.3.2.2.
Enthalpic form of the kinetic energy equation
For a divariant fluid we have the thermodynamic relation:
1
or:
ii i
dp p h s
dh Tds T
xx x
¬
ss s
ss s
®
Substituting the preceding expressions into equation [4.27], we obtain:
j
ij
i
i
i
i
i
x
u
x
s
TuhU
V
x
u
V
t w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
W
UUU
22
22
[4.28]
The reader will note that equation [4.28] is an equation of essentially mechanical
origin, even if it involves thermodynamic functions.
4.3.2.3.
Applications
4.3.2.3.1.
The constant density fluid
When the density of a fluid is uniform, we can introduce the driving pressure p
g
previously defined in equation [4.27]. We then derive the kinetic energy equation:
)3,2,1,(
22
22
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
ji
x
up
V
x
u
V
t
j
ij
ig
i
i
W
UU
[4.29]
Note the absence of any coupling between the mechanical and the
thermodynamic phenomena for a constant density fluid.
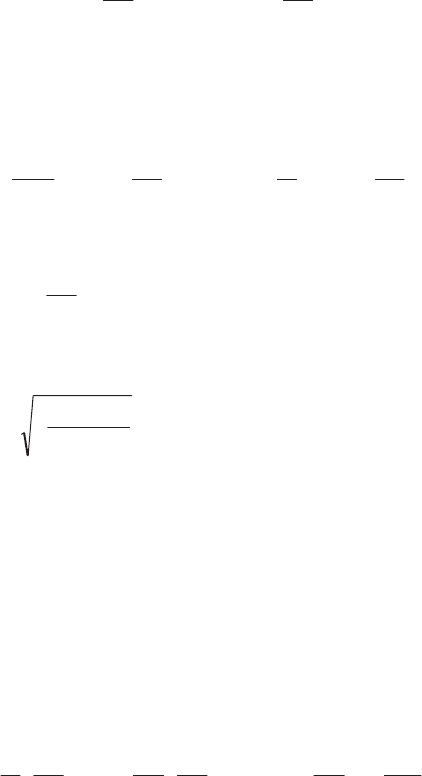
166 Fundamentals of Fluid Mechanics and Transport Phenomena
Equation [4.29] leads to the definition of total pressure p
t
and total driving
pressure p
gt
:
22
22
V
pp
V
pp
tggt
UU
If we assume that the flow is steady and the viscous stresses are zero, the first
term on the left-hand side and the right-hand side of equation [4.29] can be removed,
giving:
0
2
or0
2
22
¹
·
¨
¨
©
§
¹
·
¨
¨
©
§
w
w
V
p
dt
dV
p
x
u
g
g
j
j
U
U
[4.30]
Bernoulli’s first theorem: in steady inviscid flow, the total driving pressure
2
2
V
pp
ggt
U
is constant on a trajectory or here on a streamline.
Bernoulli’s first theorem can also be written:
U
ggt
pp
V
2
[4.31]
We thus have, in differential (Lagrangian) form:
0 VdVdp
g
U
.
This expression shows that the driving pressure is a decaying function of the
velocity modulus.
4.3.2.3.2.
The flow of compressible fluids
With the exception of flows generated by natural convection, which are due to a
density gradient, the
effects of gravity are negligible in gas flows. Kinetic energy can
be written:
j
ij
i
i
i
i
i
x
u
x
s
Tuh
V
x
u
V
t w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
W
UUU
22
22
[4.32]

Fluid Dynamics Equations 167
For steady flows of inviscid fluid undergoing isentropic transformations, this
relation can be written as:
0
2dt
d
:or0
2
¸
¸
¹
·
¨
¨
©
§
w
w
V
h
x
h
u
j
t
j
This is Bernoulli’s first theorem:
total enthalpy 2
2
Vhh
t
is constant on
streamlines in steady inviscid flow
. It is equal to the enthalpy generation h
0
which
corresponds to zero velocity. We have:
hhVor
V
hhh
tt
2:
2
2
0
[4.33]
In differential form, following a streamline, we obtain:
0 VdV
dp
dh
t
U
[4.34]
Here again, pressure is a decaying function of the velocity modulus along a
streamline.
4.3.2.3.3.
Case of a perfect gas: the Saint-Venant relation
Consider a divariant fluid evolving according to an
isentropic transformation
along its trajectory; the quantities
U
and c (sound velocity) are then functions of one
variable,
p for example. Relation [4.34] is a differential equation whose integration
gives the pressure-velocity relationship. Consider the case of a perfect gas for which
we have:
JJ
U
U
0
0
p
p
Substituting this expression into [4.34] gives:
0
1
0
1
0
VdV
p
dp
p
VdV
dp
J
J
UU

168 Fundamentals of Fluid Mechanics and Transport Phenomena
Integrating and taking as reference (
p
0
,
U
0
, T
0
) the initial or generation
conditions,
where the velocity is zero, we obtain the Saint-Venant relation:
»
»
»
»
¼
º
«
«
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
J
J
UJ
J
1
00
0
1
1
2
p
p
p
V [4.35]
As the pressure and thermodynamic temperature cannot be negative, the Saint-
Venant relation implies the existence of a maximum velocity V
max
:
1
2
1
2
0
0
0
max
JUJ
J
c
p
V .
The local sound speed c is given by relation [1.25]
S
pc
U
ww
2
. We obtain:
rT
p
c
J
U
J
[4.36]
Let us denote by c
*
the velocity V in conditions (called critical conditions) where
the fluid velocity is equal to the local sound speed:
*
ccV . Considering a
perfect gas of specific enthalpy
TCh
p
, and substituting the preceding definitions
into [4.33] expressing the conservation of total enthalpy, we obtain:
2
*
2
max
222
0
12
1
2212
c
V
VcV
TCTC
pp
J
J
J
The velocities c
*
and V
max
are defined by generation conditions.
V
p
p
0
p
*
c
*
O
*max
1
1
cV
J
J
Figure 4.2.
Saint-Venant relation
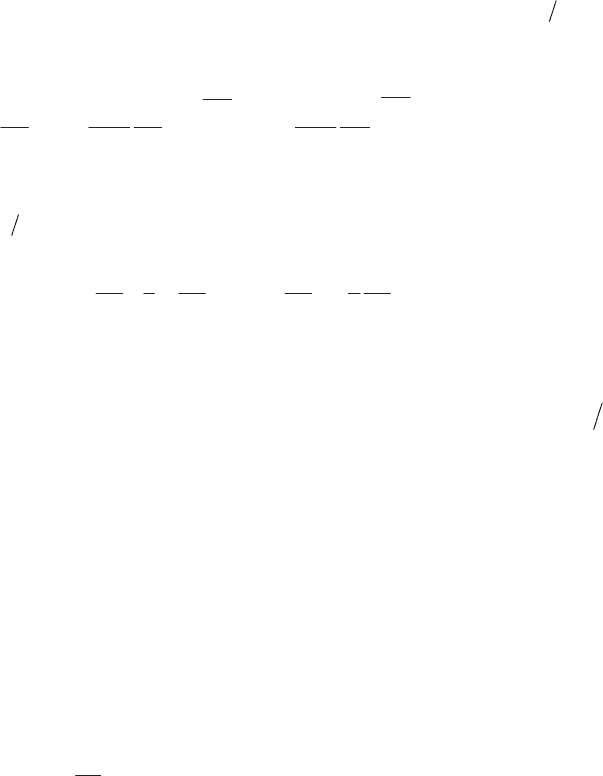
Fluid Dynamics Equations 169
Solving the Saint-Venant relation with respect to pressure,
2/1
00
)(
UJ
pc
c
being sound velocity in generation conditions, we obtain:
1
2
0
2
1
2
0
0
0
2
1
1
2
1
1
»
»
¼
º
«
«
¬
ª
»
»
¼
º
«
«
¬
ª
J
J
J
J
J
J
U
J
J
c
V
V
pp
p
The development of pressure to fourth order with respect to Mach number
00
M cV is:
24 22
00 0 0
22
00
11
... (1 ...)
28 2 4
VV VV
pp
cc
For values of p close to p
0
, i.e. for small enough Mach numbers, the Saint-
Venant relation reduces to formula [4.31] for an incompressible fluid, whose
application to compressible fluid induces a relative error amounting only to
4M
2
0
.
Then by using Bernoulli’s theorem to air flowing at 70 m.s
-1
(2.0#M
0
), error is
only 1%. For pressure calculations, Bernoulli’s incompressible relation can be used
for many industrial or domestic problems of gas flowing such as ventilation, wind
effects, etc.
We will look at some other consequences of the Saint-Venant relation in section
5.5.
4.3.2.3.4.
Variation of the mass flux density and the Hugoniot relation
The mass flux density (mass flow per unit section of a stream tube) is equal to
U
V. Replacing dp in equation [4.34] by its expression
U
dcdp
2
, we obtain:
dV
c
V
d
2
UU
[4.37]
or, introducing the Mach number M = V / c:
dVMVd
2
1
UU
[4.38]
We see that the mass flux density
U
V increases with the Mach number in
subsonic flows while it decreases in supersonic flows; it is at maximum for
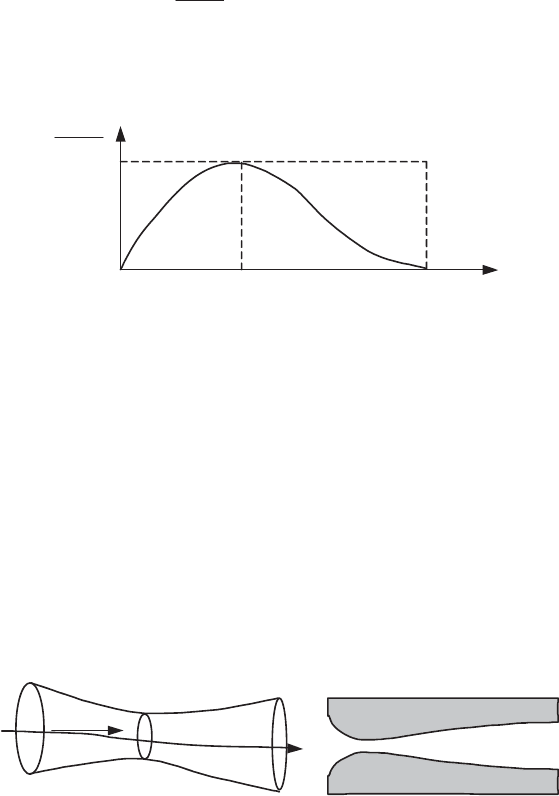
170 Fundamentals of Fluid Mechanics and Transport Phenomena
*
ccV . Variations of
**
c
V
U
U
as a function of the velocity V are shown in
Figure 4.3 (
U
*
is the critical density). Note that two velocity values correspond to the
preceding ratio, one subsonic, the other supersonic.
V c
*
O V
max
**
c
V
U
U
1
Figure 4.3.
Variation of the mass flux density (with reference
to critical conditions) as a function of the flow velocity
Consider a stream tube of variable cross-section
S
, small enough for the
properties
Vp
,,
U
of the fluid to be uniform in any cross-section (this is the
approximation of the flow by slices).
For an
incompressible fluid
(
d
U
the mass conservation
SV =
const
is
manifest in the fact that the cross-section and the velocity are inversely proportional.
In the stream tube shown in Figure 4.4a, the velocity increases to a maximum which
occurs at the throat of the minimal section S
c
, then decays. According to [4.34], the
driving pressure is minimal at the throat.
V
G
S
S
c
x
(b)(a)
Figure 4.4.
(a) Flow in a stream tube; (b) nozzle
Consider now the case of a
divariant
compressible fluid
which undergoes
isentropic transformations along a stream tube. The thermodynamic and mechanical
quantities of the fluid now only depend on one variable (pressure, velocity, cross-

Fluid Dynamics Equations 171
section, etc.). We can write the conservation of mass flow
SV
U
in differential form
in this stream tube (
0
VSd
U
); taking account of [4.38], we obtain Hugoniot’s
differential relation:
01
2
2
¸
¸
¹
·
¨
¨
©
§
S
dS
V
dV
c
V
VS
VSd
U
U
[4.39]
Equation [4.39] cannot be solved with respect to the derivative
dV/dS
in a
velocity interval in which we have the velocity
V = c
(critical conditions), this value
corresponding to a singular point of this differential equation.
On the other hand, we can always solve equation [4.39] with respect to
dS/dV
,
showing that the cross-section S of the tube is a decreasing function of the velocity
in subsonic flow (V<c), but increasing for supersonic flows (V>c).
The minimum cross-section corresponds to:
– either a velocity
maximum in a subsonic flow
, as in the incompressible case;
– or a
velocity equal to the local sound speed
.
As the mass flow rate
SV
U
is constant, the area
S
of the cross-section varies
inversely with the product
V
U
studied earlier (Figure 4.3). The maximum mass
flux density
V
U
occurs in the throat of the nozzle, where the cross-section is
smallest. However, this quantity
V
U
can only take values smaller than the critical
value
U
*
c
*
. So, the mass flow rate cannot exceed the critical value
U
*
S
c
c
*
calculated
in the throat cross-section. The mass flow rate may be obviously less than this
maximum value, the velocity in cross-section
S
c
then being smaller than the sound
velocity.
This configuration is characteristic of nozzles (Figure 4.4b). Note that for a given
value of the cross-section S or the quantity
ȡ
SV,
there are two corresponding
velocities, which explains the difficulty encountered when we try to solve equation
[4.39] for the velocity
V
. We will return to look at the consequences of this situation
in section 5.5.4.
4.3.3. The vorticity equation
We have seen that for a mechanical system, we can consider a dynamic moment
(section 3.2.1) taken about the inertia center of the system in a reference frame
which is parallel to a Galilean reference frame. The instantaneous rotational

172 Fundamentals of Fluid Mechanics and Transport Phenomena
movements in a fluid are characterized by the vorticity vector
Vrot
G
G
Z
2 ([3.38]).
The vorticity equation can be obtained by taking the curl of the Navier-Stokes
equations [4.14]. Assuming body forces to derive from a potential, and using the
identity:
AagradArotaAarot
G
G
G
.. [4.40]
we obtain, for any fluid:
¸
¸
¹
·
¨
¨
©
§
w
w
W
U
U
U
divrotpgradgradVVrotrot
t
Vrot 11
2
G
G
[4.41]
For a divariant fluid, we have, applying formulae [4.19] and [4.40]:
¸
¸
¹
·
¨
¨
©
§
w
w
W
U
divrotsgradTgradVVrotrot
t
Vrot 1
G
G
[4.42]
Assuming a Newtonian fluid with constant viscosity and density, the vorticity
equation can be written, with [4.21]:
ZXZ
Z
'
w
w
Vrot
t
G
G
[4.43]
For a 2D velocity field, the vorticity vector
Z
G
has only one component. This fact
leads to very important specific properties, in particular in the study of turbulence
([COU 89], [MAT 00], [TEN 72])
The reader will note that the vorticity equations in inviscid flows are identical for
homoentropic and incompressible fluids.
4.3.4. The energy equation
4.3.4.1. The total energy equation
4.3.4.1.1.
General expression as a function of the stress tensor
We will here apply the same procedure which we applied for an elementary
material system (section 3.2.5.1).
