Peube J-L. Fundamentals of fluid mechanics and transport phenomena

Подождите немного. Документ загружается.

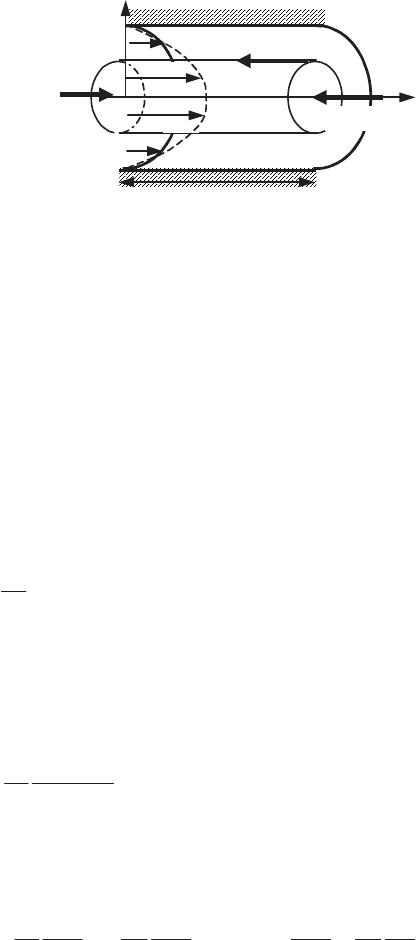
Physics of Energetic Systems in Flow 143

(0)

S

u(r)

SW

(L)Sr

(0)

(L)=p

(0)-'p



Figure 3.13.

Established flow in a circular tube

The velocity distribution can be calculated using equation [3.46], along with the

phenomenological law for the viscous fluid. Using physical law [3.47] in relation

[3.46], we obtain an expression for the derivative

u’(y) as a function of the radius r

and the pressure gradient; integrating and taking the velocity equal to zero at the

wall (

), we obtain a parabolic velocity distribution. The mass flow q

can be

obtained as a function of the pressure gradient by integrating the velocity over a

cross-section.

We define the mean mass flux velocity

using the mass flux q

This leads to the following results:

 Newtonian fluid with constant viscosity:

=cte. The velocity distribution is

parabolic (Figure 3.14a):







[3.51]

We can deduce the volume flow rate

in the tube and the flow velocity u

as a

function of the pressure gradient (Poiseuille’s law):



888

[3.52]

144 Fundamentals of Fluid Mechanics and Transport Phenomena

– Bingham fluid. Using the relationship between the stresses and the velocity

gradient for the fluid ([3.50]), the velocity profile can be calculated as for Newtonian

fluids. We find a velocity distribution comprising a uniform central section

(corresponding to a bulk displacement) and two half-parabolas (Figure 3.14b).

(a) Newtonian fluid

(b) Bingham fluid

solid core

Figure 3.14.

Velocity profile for (a) a Newtonian fluid and (b) a Bingham fluid

– Ostwald-de Waele model. The physical law is no longer linear for fluids

containing strong concentrations of particles in suspension:

n 1

The velocity distribution thus calculated looks like a parabolic distribution, but

pointier if

n is greater than 1, and flatter if n is less than 1.

3.4.2.5.2.

The Rabinowitsch-Mooney relation

The law for the drop in driving pressure as a function of the mass flow in a

Poiseuille flow depends in a complex way on the law governing the viscous

behavior of the fluid, as this law must be integrated over the radius. The

measurement of pressure-drop in capillary tubes does not directly give the physical

law governing viscous behavior; such measurements must be specially treated in

order to determine the physical laws. We will here outline the principle of the

method (Rabinowitsch-Mooney) for obtaining the relationship between the viscous

stress

and the velocity gradient uƍ(r).

Physics of Energetic Systems in Flow 145

We note first of all that the pressure gradient measured can be expressed using

[3.46] as a function of the wall friction

(which is defined as the stress exerted by

the fluid on the wall,



RW ), from which we obtain:



with:

 rdpR

R

 Rdx

  

[3.53]

The measurement gives a relation between the flow rate

and the pressure

gradient or, according to [3.53], between the viscous wall stress

and the flow rate

 which can be written:





pvv

[3.54]

We obtain a relation between the flow rate and the velocity gradient using

integration by parts on the defining relation for the flow rate:



³³³

S S S

RRR

rrudrudrq

Formula [3.53] allows us to use the viscous stress

W as a variable in place of the

radius r in the expression for the flow rate, which can be written (noting that

W

(R)):

WW

[3.55]

Then, from [3.54], the relation





q W

is known; we thus differentiate the two

sides of [3.55] with respect to







which finally gives:





[3.56]

146 Fundamentals of Fluid Mechanics and Transport Phenomena

Relation [3.56] between the velocity gradient



Ru'

and the stress

W

is the

relation sought between the velocity gradient and the viscous stress.

3.4.2.5.3.

Diverse remarks

The flow between two fixed parallel planes separated by a distance 2e can be

treated in a similar fashion. We find, for a Newtonian fluid of dynamic viscosity

the following velocity distribution

u(y), flow rate q

and mass-flow velocity u



;

2322

Flows of Bingham or Ostwald-de Waele fluids produce results analogous to

those obtained in the case of the circular cylinder.

The preceding results remain valid when the thickness

e varies slowly, in other

words when the planes are weakly non-parallel. These results are the basic laws used

for the theory of dynamic lubrication flows in a thin fluid film (oil or gas) of slightly

variable thickness between a moving wall and a fixed wall; such a flow generates

pressures high enough to support heavy rotating devices without solid contacts in a

bearing ([GUY 01]).

2) It is necessary to note that experimental results agree with the preceding

results provided the mass-flow velocity is not too great. In fact, the condition which

must be satisfied involves the Reynolds number

Re which, for a circular tube of

diameter

D equal to 2R, is written:

The value of the Reynolds number

Re must be less than about 1,850 for the

preceding theoretical results to agree with experiments. Above this value the flow

becomes unstable and turbulent, and this entirely changes the momentum transfers,

as stated earlier in section 3.4.1.3 ([MAT 00], [SCH 99], [TEN 72])

3.4.3. The Newtonian fluid

3.4.3.1. Definition of viscosity

We will place ourselves in the context of linear thermodynamics where the

relationship between the causes (the strain-rate tensor

) and effects (the viscous

stress tensor

) is linear. Furthermore, as the fluid matter considered has isotropic

Physics of Energetic Systems in Flow 147

properties, and as geometric space is homogenous and isotropic, this relationship

cannot involve any preferred direction. As a consequence of this, the two preceding

tensors must have the same principal axes. Hence, they must be proportional,

excluding the addition of an isotropic tensor proportional to the trace

Vdiv

of the

strain tensor. The linear relationship sought between the two preceding tensors

(Newton’s law) can thus be written:

ijij

GPKPGPKPHW







2 [3.57]

Linear relation [3.57] introduces

dynamic viscosity

and bulk viscosity

. The

latter corresponds to the friction introduced by a purely spherical expansion, for

which the diagonal terms of the strain-rate tensor are equal, and the off-diagonal

terms are zero:

Vdiv

Thus:

Vdiv

KWWW

332211

This relation shows that the viscosity

is indeed associated with a expansion

velocity, and that this coefficient must be positive in order to represent friction. In

what follows we will neglect the effects of bulk viscosity, which is only important

for phenomena comprising very strong expansion rates, such as shock waves, very

high frequency ultrasound, etc.

3.4.3.2.

Properties of viscosity

Dynamic viscosity

is associated with friction in the sliding of fluid layers over

one another. It is expressed in Pascal.second (Poiseuille or decapoise).

The values of dynamic viscosity under normal conditions are, for air and water:

 air: P



= 17.08 × 10

-6

Pa.s (same order of magnitude for gases);

water: P



= 1.793 ×10

-3

Pa.s.

The variability in the order of magnitude of the viscosity of liquids compared to

the viscosity of water is a little greater for usual liquids, with the exception of oils

and glycerine, which have very high viscosity (from 10

-2

to 1 Pa.s).

148 Fundamentals of Fluid Mechanics and Transport Phenomena

In section 3.4.1.3 we have given a rough estimation of the viscosity of a gas. As

thermal agitation increases with temperature, changes occur in momentum exchange

at the molecular level. The viscosity increases with increases in the absolute

temperature of gases in accordance with the following (Sutherland) formula, in

which C is a constant which depends on the gas (C=142K for air):

The viscosity decreases quite rapidly with temperature for liquids, because the

intermolecular forces responsible for viscosity in condensed media have a less

vigorous action on account of increased thermal agitation (section 3.4.1.3).

The quantity

, called the kinematic viscosity, is expressed in m

-1

EXERCISE

–

Calculate the components of the viscous stress tensor

at all points of the flow defined by the velocity field u

=kx

=0;

 in the vicinity of a solid boundary.

3.4.3.3.

Expression of viscous volume forces

We have seen (section 3.4.1.2) that the action of viscous stresses in matter is

equivalent to a volume source

div (or

jij

xww

in tensor notation). Assuming a

variable viscosity, we obtain, from [3.57]:





PKP

At constant viscosity this simplifies to:



ijj

xxx

PKP

The first term of

jij

is equal to

u' , where

u' are the components of

the Laplacian vector

Physics of Energetic Systems in Flow 149







VdivgradVrotrotV

 '

Replacing

with the above expression gives, in vector notation:



VdivgradVrotrotVdivgradVdiv



'

KPW

[3.58]

Usually expansion velocities are weak compared with shear velocities and only

the first term





Vrotrot

div remains:





Vrotrotdiv

 [3.59]

With the preceding approximation, formula [3.59] can be written in Cartesian

coordinates:

x ww

[3.60]

This page intentionally left blank

Chapter 4

Fluid Dynamics Equations

This chapter is devoted to general equations describing the dynamics of fluid

flows and of the associated transfers. Writing the balance equations for extensive

quantities leads to the equations of fluid dynamics with heat or mass transfers which

take on either local or global forms, and which allow the separation of input and

output mechanisms and sources of extensive quantities. The energy equation then

allows us to discern the interactions between thermodynamics and the movement of

the fluid matter. The main boundary conditions which must be associated with the

partial differential equations are then discussed. Because of the invariance of

physical laws with respect to unit systems, similarity relations allow us to

characterize dynamic and energy problems by means of non-dimensional

parameters.

4.1. Local balance equations

4.1.1. Balance of an extensive quantity G

4.1.1.1. The global balance equation

In matter, the physical phenomena associated with the scalar quantity G are

governed by the volume sources

and fluxes characterized by the flux density

vector

. We perform a balance for

over the domain D associated with matter in

motion, in other words on a closed system in the thermodynamic sense (no exchange

of matter with the exterior). This balance can be written in the same way as in a

fixed medium, the material derivative (section 3.3.3.3) replacing the temporal

derivative (section 2.1.4.1):

152 Fundamentals of Fluid Mechanics and Transport Phenomena



dsnqdvdsnu

GjG

³³³³³

 

DDD

[4.1]

The first term

of the left-hand side of equation [4.1] represents the

variation rate in the amount of the quantity

contained in D, expressing an

accumulation

in D.

The second term

dsnug

is the flux (convective flux) of the quantity G

leaving the surface 6.

The first term of the right-hand side

is a

volume source

, in other words

a creation of the quantity

, most often by means of the transformation of another

extensive quantity.

The second term

dsnq

jGj

is a

convective flux of the quantity G leaving the

surface

6 characterized by physical quantities localized on the surface 6.

4.1.1.2.

Local balance equation

We can now transform the surface integrals of equation [4.1] into volume

integrals:



³³





[4.2]

As balance integral [4.2] is true in any domain D, we can derive a local relation

under the usual regularity conditions of the functions considered:









[4.3]

When the volume quantity is a vector,

(or 1,2,3)

i  , we have a balance

equation for each of its components, which can be written in the vector form:



Gij

Gi G G

div g V div q

tx x t

   

ww w w

JJJG JJJG