Peube J-L. Fundamentals of fluid mechanics and transport phenomena
Подождите немного. Документ загружается.


Fluid Dynamics Equations 153
4.1.2. Interpretation of an equation in terms of the balance equation
The terms in equation [4.3] each have a specific form corresponding to physical
mechanisms which we have discussed earlier (section 2.1.3.3). Consider a partial
differential equation which can be written in the form [4.3]:
j
j
x
q
t
f
w
w
w
w
V
[4.4]
We can integrate equation [4.3] over a
geometric domain
D
to give:
dsnqdvdv
t
f
j
j
³³³
6
w
w
DD
V
[4.5]
We will interpret
f
as the volume density of a quantity
F,
the amount of which
present in
D
is equal to
.
¨
fdv
D
The first term
dv
t
f
³
w
w
D
of equation [4.4] represents
the variation rate in the amount of the quantity
F
contained in
D
.
On the right-hand side of equation [4.4], we have separated the terms which can
be written in the form of a divergent vector
q
i
expressed using data or functions of
the problem, and those which cannot be written in this form. In integrating over the
domain
D
, the terms written in the form of a divergence have been transformed into
flux integrals of the vector q
i
on the external surface 6 of the domain
D
: they can
thus be interpreted as transfers of the quantity
F
by the vector
q
i
. These transport
terms are thus the input-output of the quantity
F
in
D
, in other words quantities
gained by
D
from (or lost to) the exterior through the surface
6
.
On the other hand, if the vector
q
i
can be written in the form
ii
vfq
, we
interpret the term
j
j
x
q
w
w
as representing the convective transport of the quantity
F
by
the velocity field
v
i
, whose physical interpretation is not important here. In fact, the
vector
q
i
will most often be the sum of a variety of terms with different physical
interpretations. In general, a flux term will only transport a quantity without creating
any; in balance equations which are integrated over a large domain bounded by a
surface
6, fluxes which only have local effects will not appear
.
Terms which cannot be written in the form of the divergence of a vector having a
physical meaning consistent with the problem considered cannot be interpreted as
flux terms. Furthermore, take in this case a balance equation by integration on a

154 Fundamentals of Fluid Mechanics and Transport Phenomena
domain
D
which encloses a zone containing the phenomena to be studied. As the
volume integral of non-divergent terms cannot be written as a surface integral, it is
not possible to characterize as an input or an output the detailed repartition of
quantity of
F
injected in this domain by the source
ǻ
. This distinction between
these two kinds of terms is very often used in turbulence theory ([COU 89], [MAT
00], [TEN 72]).
We will have occasion to use this interpretation.
4.2. Mass balance
4.2.1. Conservation of mass and its consequences
4.2.1.1.
The equation of mass conservation
Mass is strictly conserved (no sources or fluxes of mass in a barycentric
reference frame); we let
U
g
. We obtain from [4.3] the equation (known as the
continuity equation):
0
w
w
w
w
i
i
x
u
t
UU
[4.6]
or alternatively:
0
w
w
i
i
x
u
dt
d
U
U
[4.7]
which shows that the variation rate of the density
dt
d
U
U
1
of a fluid particle is
compensated by the volume expansion rate
i
i
x
u
w
w
.
The flow of an incompressible fluid (liquid or gas moving at low velocity) of
variable density satisfies
0 dtd
U
: matter is displaced with its specific mass on a
trajectory (obvious a priori).
4.2.1.2.
Consequences of the mass conservation equation
4.2.1.2.1.
Writing the balance of a mass quantity
Let g be a mass quantity (
gg
U
); by means of a simple calculation the
following two useful relations can be immediately verified:

Fluid Dynamics Equations 155
dv
d
t
dg
dvg
d
t
d
UU
³³
DD
[4.8]
dt
dg
x
gu
t
g
x
ug
t
g
i
i
i
i
U
UU
w
w
w
w
w
w
w
w
[4.9]
The balance equation of the quantity G can be written using the mass quantity g:
j
Gj
G
i
i
i
i
x
q
x
gu
t
g
x
g
u
t
g
dt
dg
w
w
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
V
U
U
UU
[4.10]
4.2.1.2.2.
Stream functions
In the particular case of problems with two variables, the solution of equation
[4.6] or [4.7] can immediately be written by means of a stream function
\
:
a) For a 1D compressible flow:
t
u
xx
u
t w
w
w
w
w
w
w
w
\
U
\
U
UU
0 [4.11]
b) For a steady plane 2D flow:
x
v
y
u
y
v
x
u
w
w
w
w
w
w
w
w
\
UU
\
UU
UU
00
0 [4.12]
It is easy to verify that, in this case, the lines
\
=
const
are
streamlines
of the
flow
(we have
0grad.V
\U
G
).
The mass flow between two streamlines passing through the points A and B is
equal to the difference
AB
\
\
U
0
. The arc element
dydxd ,A
G
of the curve
joining A and B allows the elementary vector
dxdydn
,
A
G
of the normal of this
curve to be expressed, from which we can derive the mass flow:
ABddy
y
dx
x
dnVq
ABABAB
m
\\U\U
\\
UU
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
³³³
000
. A
G
G
c) For a
steady axisymmetric flow (where Oz is the axis of symmetry), the mass
conservation equation in a steady regime is equivalent to the following definition for
the stream function
\
:

156 Fundamentals of Fluid Mechanics and Transport Phenomena
rr
w
zr
u
z
rw
r
ru
w
w
w
w
w
w
w
w
\
U
U
\
U
U
UU
00
,0
d) For flows with constant density
U
, the densities disappear from the definition
of the stream function; in a 2D plane flow, we have:
1
2
2
1
x
u
x
u
w
w
w
w
\\
4.2.1.2.3.
Velocity fields of a viscous fluid near a solid boundary
The property which we will discuss here only depends on the mass balance and
is of course independent of the reference frame which is chosen (Galilean or
otherwise). We will consider a solid boundary P and study the velocity field in the
vicinity of some point O on this boundary. Taking rectangular axes such that the
plane O
xz is tangential to the surface (whose normal is Oy) at the point O. Assuming
the fluid to be viscous, the velocity
V
G
with components (u, v, w) is zero at the
surface (y = 0). The
u and w components of the velocity
,V
G
parallel to the wall, can
be expanded about
y in the vicinity of this point:
!
!
),,(),,(),,,(
;),,(),,(),,,(
2
2
1
2
2
1
tzxwytzxwytzyxw
tzxuytzxuytzyxu
y
z
C
x
O
Figure 4.1. Flow near a rigid wall
Substituting into the mass conservation equation [4.7] we obtain:
)(
1
2
11
yO
z
w
x
u
y
dt
d
y
v
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
U
U

Fluid Dynamics Equations 157
or, by integrating: )(
2
1
3
11
2
0
yO
z
w
x
uy
dy
dt
d
v
y
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
³
U
U
When the expansion rate is negligible or equal to zero (incompressible fluid
(section 4.2.2)), the first non-zero term of the expansion of the v component is O(y
2
).
The normal component v tends to zero more rapidly in y than the components
tangent to the wall: the velocity in the vicinity of the wall is parallel to the wall. The
wall streamline C is the streamline limit when y tends to zero (Figure 4.1).
4.2.1.2.4.
The strain-rate tensor near a solid boundary
Replacing the preceding expressions for the velocity components into the
expression for strain rate tensor [3.37], we obtain:
)(
020
22
020
1
11
1
yO
w
wdtdu
u
¸
¸
¸
¹
·
¨
¨
¨
©
§
UUH
We note the existence of shear velocities associated with a velocity field which is
quasi-parallel to the wall, and a expansion velocity which is essentially normal to
the wall.
4.2.1.2.5.
Acceleration near a solid boundary
From the preceding expressions for the velocity we can derive the expressions of
the fluid acceleration components (in the wall reference frame). Let us first consider
the component
z
u
w
y
u
v
x
u
u
t
u
dt
du
x
w
w
w
w
w
w
w
w
J
. In the general case where
dtd
U
is not equal to zero, by substituting the velocity components with their
preceding expressions, we obtain:
)(
1
)(
2
0
1
1
3
1
1
1
1
2
yOdy
dt
d
u
t
u
y
y
u
v
t
u
yO
z
u
w
x
u
uy
z
u
w
x
u
u
y
w
w
w
w
w
w
»
¼
º
«
¬
ª
w
w
w
w
w
w
w
w
³
U
U
Fluid expansion and unsteady flow variations involve the existence of terms of
order y near the wall.
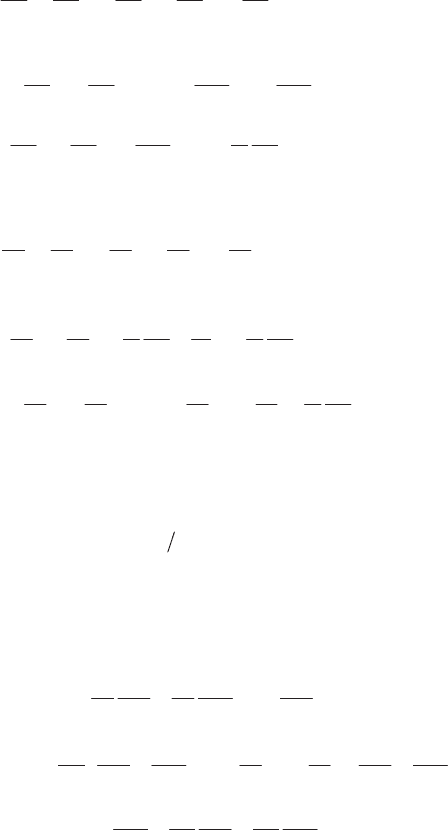
158 Fundamentals of Fluid Mechanics and Transport Phenomena
In the same way, for the second tangential component
z
w
w
y
w
v
x
w
u
t
w
dt
dw
z
w
w
w
w
w
w
w
w
J
we obtain:
)(
1
)(
2
0
1
1
3
1
1
1
1
2
yOdy
dt
d
w
t
w
y
y
w
v
t
w
yO
z
w
w
x
w
uy
z
w
w
x
w
u
y
w
w
w
w
w
w
»
¼
º
«
¬
ª
w
w
w
w
w
w
w
w
³
U
U
We finally derive the following expressions for the acceleration component
z
v
w
y
v
v
x
v
u
t
v
dt
dv
y
w
w
w
w
w
w
w
w
J
normal to the wall:
)(
1
)(
11
3
0
11
2
0
yOdy
dt
d
z
w
x
uy
z
v
w
x
v
u
yOdy
dt
d
tdt
d
y
v
v
t
v
y
y
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
»
¼
º
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
³
³
U
U
U
U
U
U
The acceleration is a linear function of the distance from the wall.
For an unsteady flow of an incompressible fluid, the expansion rate is equal to
zero so that we have
0 dtd
U
(section 4.2.2). The preceding expressions for
acceleration component
J
y
normal to the wall is O(y
2
), the tangential components
remaining O(y).
For a steady flow of an incompressible fluid, we have:
3
11111
1
2
4
11
11
11
3
3
1
1
1111
2
22
)(
2
22
yO
z
ww
x
uw
x
w
uy
yO
z
w
x
u
z
w
x
u
z
w
x
uy
yO
z
u
w
z
wu
x
uu
y
z
y
x
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
»
¼
º
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
J
J
J
In the absence of a expansion rate (incompressible fluid), the acceleration
normal to the wall is of higher order than the tangential acceleration components.

Fluid Dynamics Equations 159
4.2.1.2.6. Velocity and acceleration near a fixed surface of path lines
Consider a fixed surface which is the locus of trajectories which may be variable.
As we will later see, the practical realization of such surfaces frequently involves
walls or flow separation surfaces on which the flow of a non-viscous fluid slides.
We proceed as above, performing an expansion following the surface normal, for an
incompressible fluid:
)(
)(),,,(),,,(),,,(
)....(),,,(),,,(),,,(
00
2
10
2
10
yO
z
w
x
u
y
v
yOtzyxwytzyxwtzyxw
yOtzyxuytzyxutzyxu
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
The normal velocity component and the acceleration components can be directly
calculated:
)(
)(
)(
)(
0
0
0
0
0
2
00
00
00
2
0
0
0
0
0
2
00
yO
z
w
w
x
w
u
t
w
dt
dw
yO
z
w
x
u
z
w
x
u
tz
w
x
u
y
dt
dv
yO
z
u
w
x
u
u
t
u
dt
du
yO
z
w
x
u
yv
z
y
x
w
w
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
»
¼
º
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
w
w
w
w
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
J
J
J
The expansion is accounted for as before.
4.2.1.2.7.
Application to the study of quasi-1D flows
We often encounter flows with one or more preferred directions because these
are guided by walls presenting small angles of divergence or convergence (pipes) or
by a wall with a weak curvature (boundary layer). The same can be true in certain
zones of flows generated from almost parallel flows (jets, mixing-layers, etc.).
The preceding developments show that the velocity components and
accelerations normal to these privileged directions are small compared with the
other components. It is thus possible to neglect these components under certain
conditions: for example, the momentum or acceleration is essentially longitudinal in
a 1D flow and there can obviously be no transverse component except in the
presence of an external action. Thus, a fluid with a trajectory associated with a
160 Fundamentals of Fluid Mechanics and Transport Phenomena
curved wall will have a centripetal acceleration which is compensated by a pressure
gradient.
On the other hand, in a steady flow, the transverse component v ensures the
conservation of mass in any evolution which is not strictly parallel. Examination of
mass conservation equation [4.6] shows that the term
yv ww is necessary for the
existence of a longitudinal variation
xu ww of the u component.
The existence of a weak transverse velocity component leads to a transverse
displacement of the longitudinal momentum associated with and transported by the
fluid matter (sections 4.5.4 and 6.5).
4.2.2. Volume conservation
Volume conservation is not a physical law of matter; it results from particular
physical conditions. The flow of a liquid in ordinary conditions is a transformation
which occurs at practically constant volume, except in the case of natural
convection. We will see that the same goes for gas flows at a small Mach number.
The conservation of volume is expressed by a zero expansion velocity:
)0or(0
w
w
Vdiv
x
u
k
k
G
Taking the previous relation into account, mass balance equation [4.7] may be
written for an incompressible fluid:
0
d
t
d
U
4.3. Balance of mechanical and thermodynamic quantities
4.3.1. Momentum balance
4.3.1.1.
Dynamic equations
The quantity considered ( Vmp
G
G
) is a vector quantity: (
ii
ug
U
or
ii
ug ).
Hence we obtain the dynamic equations (
i, j = 1, 2, 3):
³³³³
6
dsndvfdv
dt
du
dvu
dt
d
jiji
i
i
VUUU
DDD
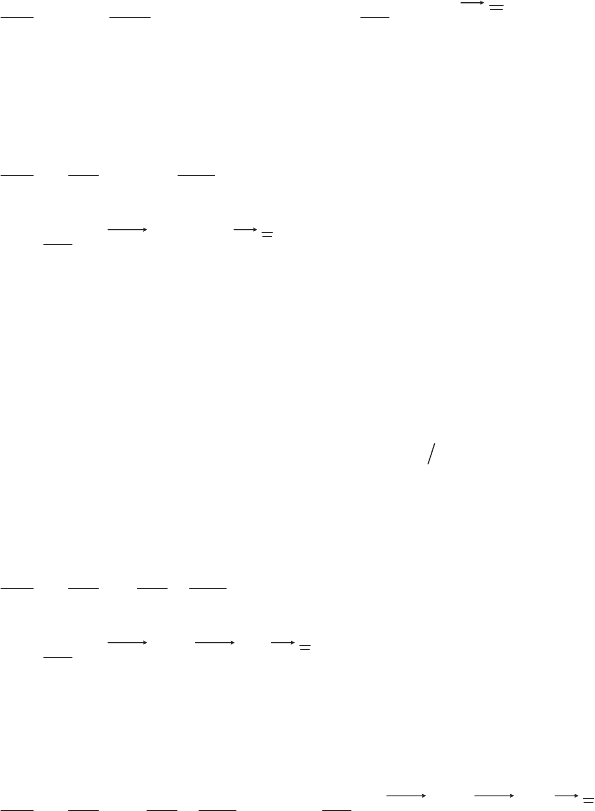
Fluid Dynamics Equations 161
with: f
i
the force mass density (for example gravity g
i
) and
V
ij
the stress tensor
(section 2.1.3.2)
Transforming the surface integral of the stress tensor using
Ostrogradsky’s theorem (section 2.1.3.3), and assuming continuous and differentiable
properties, we obtain the local dynamic equations:
VUU
V
UU
divf
dt
Vd
orji
x
f
dt
du
j
ij
i
i
w
w
G
G
)3,2,1,(
[4.13]
Replacing the stress tensor with expression [3.39], we obtain the
Navier-Stokes
equations:
WUU
W
UU
divfpgrad
dt
Vd
ji
x
f
x
p
dt
du
j
ij
i
i
i
w
w
w
w
G
G
or
)3,2,1,(
[4.14]
In a gas flow of
sufficient velocity (at least a few meters per second), the effects
of gravity are negligible and the corresponding term can be ignored. On the
contrary, pressure gradient is negligible for natural convection ([LAN 89], [SCH
99], [YIH 77]).
Case of an external force deriving from a potential U
The force f
i
may derive from a potential U (
iii
xUf ww ), essentially for
gravitation, electrostatic forces and a few simple cases of inertial entrainment forces
(when the equations are written in a non-Galilean reference frame). Navier-Stokes
equations [4.14] can then be written:
WUU
W
UU
divUgradpgrad
dt
Vd
xx
U
x
p
dt
du
j
ij
ii
i
w
w
w
w
w
w
G
or
[4.15]
In many cases of practical interest, the external force field is gravity which
derives from the potential gz, where z is a vertically ascending direction; we have:
WUU
W
UU
divgzgradpgrad
dt
Vd
xx
z
g
x
p
dt
du
j
ij
ii
i
w
w
w
w
w
w
G
or

162 Fundamentals of Fluid Mechanics and Transport Phenomena
When the fluid has constant density
U
(often incorrectly referred to as an
“incompressible fluid”), the dynamic equations can be written with the driving
pressure
z
g
p
p
g
U
, as previously defined (section 2.2.1.4.1):
)3,2,1,(
w
w
w
w
ji
xx
p
dt
du
j
ij
i
g
i
W
U
The form of the equations shows that the
cause of movement
(the local resultant
of external forces) is the
gradient of the driving pressure
. This elimination of gravity
from the dynamic equations is only of interest if the boundary conditions can also be
expressed as a function of the driving pressure alone (section 4.4.2.4).
NOTE
–
The force
f
i
does not derive from a potential in many very important
configurations, such that:
– the electromagnetic Laplace force which results from the interaction of an
electric current of density
j
G
with a magnetic field
B
G
: this produces the
volume
force
Bj
G
G
;
– the Coriolis force in a reference frame moving with an angular velocity
:
G
,
which leads to a
mass force
V
G
G
:
2.
We note that these two forces have a similar structure; thus, this produces some
analogous properties between flows in a rotating frame and flows of a fluid
conducting electricity in a magnetic fluid..
4.3.1.2.
Other expressions of the Navier-Stokes equations
Using vector expression [3.28] for acceleration, we have:
W
UU
divUgrad
pgrad
VVrot
V
grad
t
V
dt
Vd
1
2
2
w
w
G
G
G
[4.16]
For a divariant fluid, we can express the pressure as a function of the specific
enthalpy
h
and the specific entropy
s
:
¸
¸
¹
·
¨
¨
©
§
sgradT
pgrad
hgradTds
dp
dh
UU
:or [4.17]
