Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials

Подождите немного. Документ загружается.

642 Chapter

Both damping techniques stabilize Rietveld refinement but obviously

require more least squares cycles for its completion.

is worth noting, that

according to the GSAS default (which can be changed), the refinement

process is considered converged to a global minimum when the maximum

shift

(Axi) observed among all free variables is less than 11100~~ of the

corresponding standard deviation (oxi), i.e. when IAxilloxi

0.01, i

1, 2,

. .

andp is the number of free variables.'

Structure and properties of both the metal oxides and their intercalates,

which are used as examples in sections 7.7 to 7.1 1, result in high anisotropy

of crystal shapes. Distinct, plate-like or needle-like shapes of particles

(Figure 6.23, Figure 6.26, and Figure 6.31) cause a highly non-random

distribution of particle orientations even after thorough grinding and

screening. The state of the specimen often cannot be adequately described

using a simple single-parameter preferred orientation

model(s) and two

preferred orientation axes or a spherical harmonics expansion should be

employed.

parallel, the anisotropy of the particle shapes almost

necessarily causes the anisotropy in the broadening of the diffraction peaks,

which, in order to obtain a good fit, has to be accounted for as well.

Unless noted to the contrary, the initial values of peak shape parameters

used in the following five examples, were obtained from a refinement using

the experimental powder diffraction pattern of LaB6 measured on a Scintag

XDS2000 diffractometer employing Cu

radiation and a liquid nitrogen-

cooled Ge(Li) solid-state detector at typical experimental settings. These are

found on the

in the file

Scintag.prm.

We note that all profile parameters

employed in GSAS are in centidegrees (i.e. the corresponding values in

degrees have been multiplied by 100). Thus, the following settings and

initial parameters were used:

The peak shape function was a Thompson modified pseudo-Voigt.' It is

referred as No. 2 in GSAS (also see section 2.9.1 and relevant equations).

Bragg peaks were extended in the range where their calculated intensity

was greater or equal to 0.5% of the intensity at the peak maximum.

The instrumental component of

FWHM

was given by

0.7104,

-0.9565,

1.7318;

Isotropic peak broadening due to grain size and strain with

2.2952,

3.955 1, and

0 and

Peak asymmetry

2.5471.

Porosity and absorption effects were initially accounted for by using the

Suortti approach (see Eq. 2.76) with parameters a,

0.4 and a:!

0.4.

IUCr imposes the requirement

Ihxilloxi

0.05

to ensure completeness of refinements

based on single crystal data. In Rietveld

fits,

(Axi(loxi

0.1

are quite satisfactory.

Thompson,

D.E.

Cox, and

J.B.

Hastings. Rietveld refinement of Debye-Scherrer

synchrotron x-ray data from A1203,

Appl. Cryst.

20,79

(1987).

Crystal structure rejnement

643

These two parameters have a tendency to strong correlation, and they

were refined only when the quality of the pattern was sufficiently high.

The sample displacement parameter S, calculated for each particular case

from the displacement (s, in mm) obtained during unit cell refinement as:

-36000s/(nR) or S,

-144sln for the goniometer radius

250

mrn.

Cu Ka radiation wavelengths used were 1 S40562 and 1 S4439O

for

Kal

and Ka2 components, respectively.

The initial value of the phase scale factor was always 1

The initial background was set to

constant value of 100 counts or, in

some difficult cases, fitted manually and kept fixed during initial

refinement steps.

Unless noted to the contrary, a 6-parameter shifted-Chebyshev function

was employed to fit the background at later refinement stages.

The initial atomic displacement parameters were always set to

U,,,

0.015 A2, which is equivalent to Biso

8n2Uiso) of -1.2

A2.

Fractional population factors in GSAS are treated as g's (see Eq. 7.8),

while site multiplicities are automatically accounted for and cannot be

changed. Site populations, however, can be refined when needed. For

example, a population factor

0.75 for an A atom in a site with

multiplicity 4 means that 75% of the site is occupied and that there are 3

A atoms in the unit cell. Obviously, the fractional population factor

cannot be greater than unity or less than zero. When the refined value is

out of the range

this usually points to the incorrect

assignments of atom types or incorrectly located atom(s).

The majority of experimental powder diffraction patterns in the following

five examples were collected using a step scan data collection method on a

Scintag XDS2000 system equipped with a Ge(Li) solid-state detector cooled

with liquid nitrogen.

7.7

Completion of the model and Rietveld refinement of

NiMn02(OH)'

This example shows how to deal with complex preferred orientation, and

how to distinguish chemical elements with similar scattering factors (Ni, 28

Phase scales are treated differently in different realizations of the Rietveld algorithm, e.g.

in GSAS and in LHPM-Rietica. In the latter, the calculated absolute intensity is scaled

(normalized) to match the observed relative intensity, i.e. the scale factor is applied exactly

as shown in Eqs. 7.3 and 7.4. In the former, the observed relative intensity is scaled to

match the calculated absolute scattered intensity. In other words, the scale factors in GSAS

and LHPM-Rietica are related to one another as

KGSAS

lIKRietica.

R. Chen, P.Y. Zavalij, M.S. Whittingham,

J.E.

Greedan, N.P. Raju and M. Bieringer, The

hydrothermal synthesis of the new manganese and vanadium oxides, NiMn03H, MAV307

and MA0,75V4010.0.67H20 (MA

CH3NH3),

Mater. Chem.

(1999).

644 Chapter

electrons and Mn,

electrons) using x-ray powder data. Furthermore, in

this section we will also see how easy the latter can be done when neutron

diffraction data are available. The availability of the latter also illustrates

how to locate the hydrogen atom(s) in the unit cell. Finally, some important

geometrical aspects of the interpretation of the structural data will also be

considered.

The experimental x-ray pattern was collected in the range from

100'

with a

0.02O

step and a counting time of

seclstep. The initial model of

the crystal structure is listed in

Table

6.37.

Both independent metal atoms

are treated as manganese (Mnl and Mn2) and the hydrogen atom is missing

in this model. Thus, our goal is to distinguish between Mn and Ni atoms,

locate the H atom from the Fourier

map(s), and obtain accurate positional,

atomic displacement, and profile parameters.

Often, the initial stages of Rietveld refinement are both important and

difficult because the initial values of both the structural and profile

parameters may be far from the correct values. Hence, non-linear least

squares may be less stable when compared to the same at the end of the

refinement,

i.e. when nearly all parameters are close to their accurate values.

As mentioned above, variables should be refined in a proper order, usually

starting from only a few most critical parameters and then adding other

relevant variables, while continuously monitoring how previously refined

parameters continue to change. Those that correlate or begin to diverge

should be excluded from the refinement and, perhaps, constrained.

The following initial parameters were employed to begin this refinement:

Default profile parameters from the instrumental parameter file

Scintagprm

as described above in section

7.6.

Sample shift, S,

5.64

to represent sample displacements

-0.123

mm,

which was obtained together with the unit cell dimensions during the

lattice parameter refinement.

Space group

Cmc2,

and unit cell dimensions

2.8609

14.6482

5.2703

A, as determined earlier.

Structure model from

Table

6.37

with overall isotropic displacement

parameter

&,=

0.015

A2.

The starting model of the crystal structure with all of the necessary

parameters is found on the

in files

Ch7ExOSa.exp1

and

Ch7E~OSa.cif;~

the experimental pattern is located in the file

Ch7ExOS-C~Ka.raw.~

This is the main GSAS data file, which contains all structural, instrumental and other

parameters needed for refinement.

This is a Crystallographic Information File, which records all information in a standard

format acceptable by the majority of crystallographic programs, and which is required by

the majority of technical journals for publication of the structure determination results.

This is the profile (histogram) file, which contains experimental powder pattern in a

standard GSAS format. Note that this format is also suitable for LHPM-Rietica.

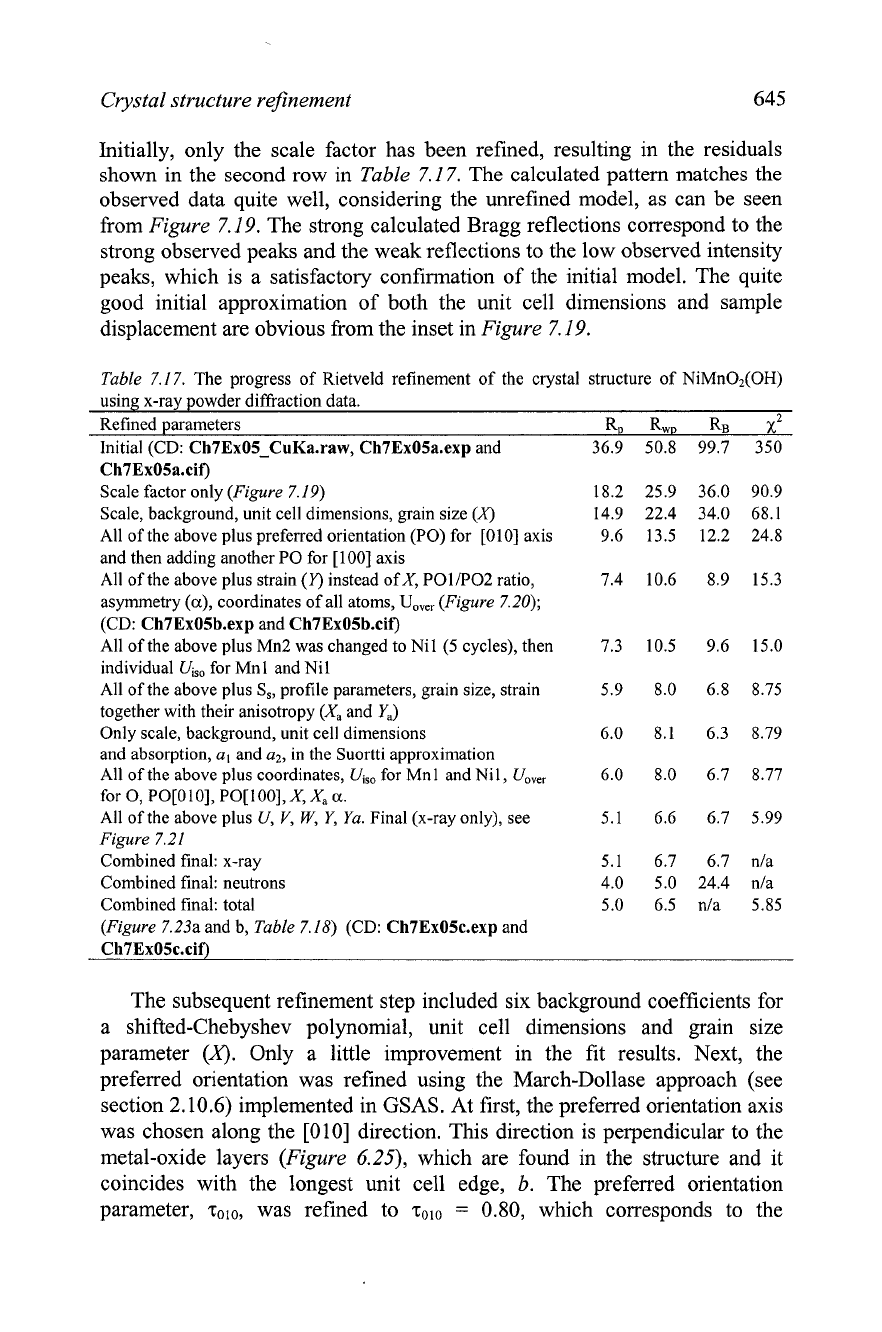
Crystal structure refinement

645

Initially, only the scale factor has been refined, resulting in the residuals

shown in the second row in

Table

7.1

The calculated pattern matches the

observed data quite well, considering the unrefined model, as can be seen

from

Figure

7.19.

The strong calculated Bragg reflections correspond to the

strong observed peaks and the weak reflections to the low observed intensity

peaks, which is a satisfactory confirmation of the initial model. The quite

good initial approximation of both the unit cell dimensions and sample

displacement are obvious from the inset in

Figure

7.19.

Table 7.17. The progress of Rietveld refinement of the crystal structure of NiMnO,(OH)

using x-ray powder diffraction data.

Refined parameters

RwD RB

Initial (CD:

Ch7ExOS-CuKa.raw, Ch7ExOSa.exp

and

Ch7ExOSa.cif)

Scale factor only (Figure 7.19)

Scale, background, unit cell dimensions, grain size

(X)

All of the above plus preferred orientation (PO) for [010] axis

and then adding another PO for [loo] axis

All of the above plus strain

(Y)

instead ofX, P01lP02 ratio,

asymmetry (a), coordinates of all atoms,

U,,,,.

(Figure 7.20);

(CD:

Ch7ExOSb.exp

and

Ch7ExOSb.cif)

All of the above plus Mn2 was changed to Nil (5 cycles), then

individual

Ui,,

for Mnl and Nil

All of the above plus S,, profile parameters, grain size, strain

together with their anisotropy

(X,

and

Ya)

Only scale, background, unit cell dimensions

and absorption, a, and

a2,

in the Suortti approximation

All of the above plus coordinates,

Ui,,

for Mnl and Nil,

U,,,

for 0, PO[O lo], P0[100],

All of the above plus

Ya. Final (x-ray only), see

Figure 7.21

Combined final: x-ray

Combined final: neutrons

Combined final: total

(Figure

7.23a and b, Table 7.18) (CD:

Ch7ExOSc.exp

and

Ch7Ex05c.cif)

The subsequent refinement step included six background coefficients for

a shifted-Chebyshev polynomial, unit cell dimensions and grain size

parameter

(3.

Only a little improvement in the fit results. Next, the

preferred orientation was refined using the March-Dollase approach (see

section 2.10.6) implemented in GSAS. At first, the preferred orientation axis

was chosen along the

[010] direction. This direction is perpendicular to the

metal-oxide layers

(Figure

6.25),

which are found in the structure and it

coincides with the longest unit cell edge,

The preferred orientation

parameter, ZO~O, was refined to

z~~~

0.80, which corresponds to the

646

Chapter

preferred orientation magnitude of

2.73.'

second preferred orientation

axis, [loo], was added after the first, and this choice was based on the

presence of metal oxide chains along the shortest unit cell edge, a. Both

preferred orientation parameters were refined together with other variables

previously included in the least squares, resulting in a substantial lowering of

all residuals (row

in Table

7.1

7).

The preferred orientation axes could be

easily predicted in this structure by comparing the unit cell dimensions and

simple geometrical analysis of the model.

many instances, the longest unit

cell dimension (in this material the b-axis), which is perpendicular to the

layers formed in the crystal structure, is also parallel to the shortest

dimension of the plate-like crystallites.

18.16%

NiMnO,(OH),

R,,

25.91

10 20 30 40 50 60 70 80 90 100 110

Bragg angle,

(deg.)

Figure

7.19.

The observed and calculated powder diffraction patterns of NiMn02(OH) after

the initial Rietveld refinement with only the scale factor determined. The inset clarifies the

range between

and

90"

28.

The difference

(KObs

KCalc)

is shown using the same scale as

both the observed and calculated data but the plot is truncated to fit within the range

[-1500,

15001

for clarity.

The magnitude of the preferred orientation is the ratio between the maximum and the

minimum correction factors, which in this case, is the ratio between the correction factors

for reflections whose reciprocal lattice vectors are parallel to

d*olo

and those, which are

perpendicular to

d"olo,

i.e.

TII/Tl.

Crystal structure refinement

647

Similarly, the shortest unit cell dimension is usually parallel to the chain-

like formations in the structure (if any) and, simultaneously, to the longest

dimension of the needle-like crystallites.

NiMn02(OH), the a-axis is much

shorter than the two others: the needle-like crystallites are elongated along

the

[

1001

direction, with the additional preferred orientation axis

[O 101

perpendicular to the flat sides of the needles (see the inset in

Figure

6.23).

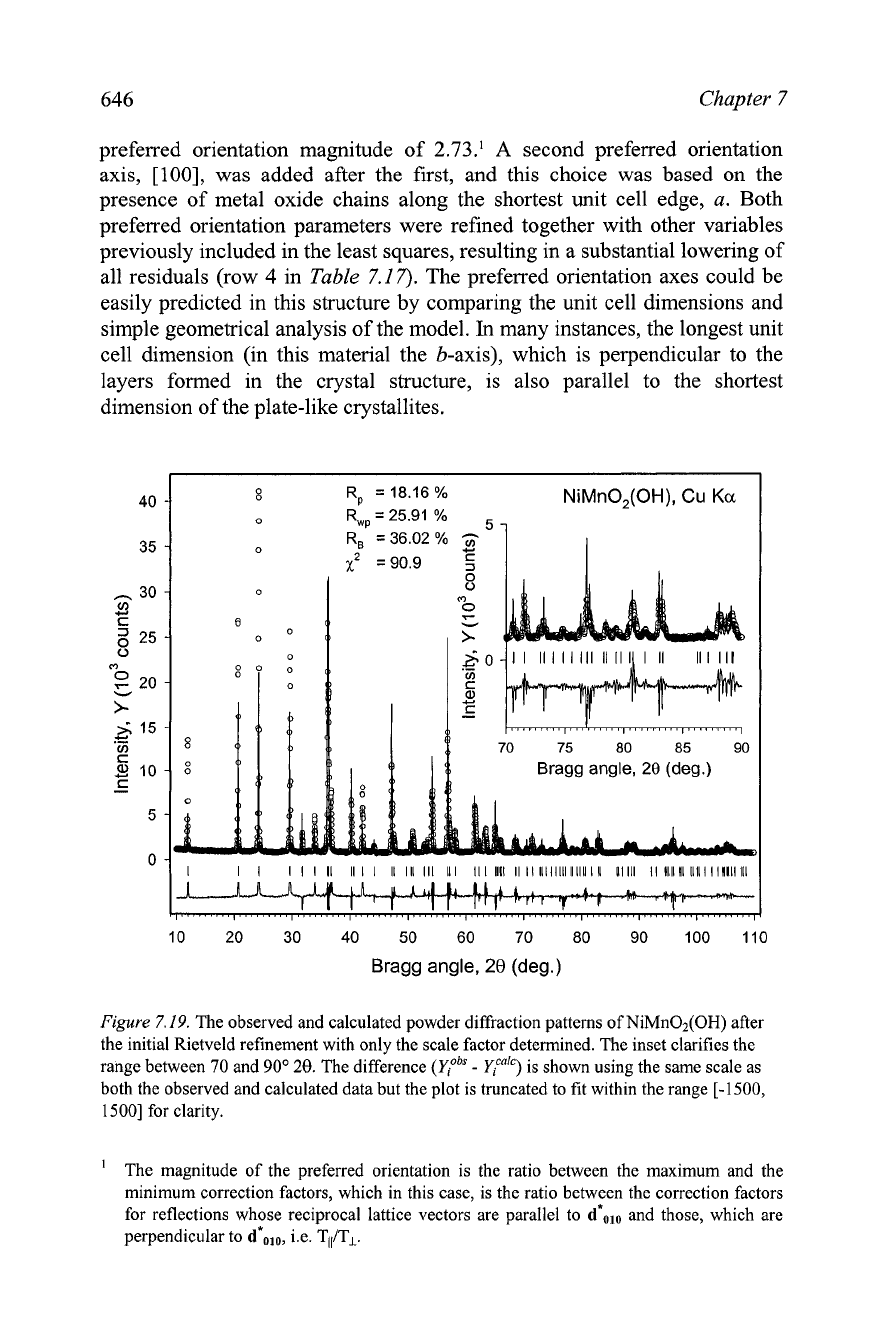
When the two preferred orientation axes are assumed, the ratio between

them should be refined as well. This was done subsequently, together with

the refinement of the coordinates of individual atoms, overall isotropic

displacement parameter,

U,,,,,

and peak asymmetry,

The resulting fit is

substantially improved, as shown in

Figure

7.20. It is clear, however, that

there are still some differences between the observed and calculated

intensities, as well as in the peak shapes

(e.g. see the inset in

Figure

7.20,

where some calculated peaks appear too narrow when compared with the

observed peak shapes).

NiMnO,(OH),

KCL

Bragg

angle,

20 (deg.)

10 20 30 40

60 70 80 90 100 110

Bragg angle,

(deg.)

Figure

7.20.

The observed and calculated powder diffraction patterns of NiMn02(OH) after

preferred orientation, coordinates of all atoms and the overall displacement parameter were

refined in addition to the scale factor, unit cell dimensions, background, grain size and strain

effects, and peak asymmetry. The insert clarifies the range between

and

90'

20.

648

Chapter

The next structure determination step is to distinguish the Mn and Ni

atoms in two positions, presently treated as manganese. There are several

possible ways of accomplishing this task:

Refining individual isotropic atomic displacement parameters with a

larger value pointing to the lighter atom and a smaller or even negative

displacement parameter indicating the heavier atom. This method works

well in refinements using single crystal diffraction data or very precise

powder data, and usually for chemical elements with substantial

differences in the scattering ability (number of electrons),

e.g. see section

7.3.3.

Refining site population factors: this is similar to the previous approach

but is a more appropriate way of testing for the scattering power of an

atom because the multiplication of the atomic number of the element,

currently present on a certain site, by its fractional occupation factor

results in the approximate number of electrons in the element that should

occupy the given site.

Conducting the refinement using all possible combinations of the

elements and then selecting the best model based on the resultant figures

of merit. This approach may be time consuming if a large number of

permutations are possible. However, in the case of NiMn02(OH), only

two possibilities exist: Mnl is Mn and Mn2 is Ni, or Mnl is Ni and Mn2

is Mn.

Analyzing the geometry of the model. This approach is nearly always

used in molecular compounds, even when single crystal data are

available. The analysis involves prior knowledge of possible bond

distances, angles, coordination polyhedra, etc.

Employing information other than Cu

x-ray diffraction data, e.g.

anomalous scattering near the K-absorption edge of one of the metals,

neutron diffraction data (see below), andlor spectroscopic results.

Despite a variety of available methods, some of them may not always

work well.

this case, the first three approaches based on x-ray diffraction

data did not allow clear differentiation between Mn and Ni atoms because

the differences between atomic displacement parameters, site populations

and standard figures of merit were not statistically significant. However,

quite different environments of the two independent metal atoms suggest

that a geometrical analysis may be helpful.

Thus, the bond valence sum method,' which is used mainly to

differentiate between the oxidation states of chemical elements rather than

Bond valence sum is calculated using interatomic distances and empirical bond valence

parameters tabulated for each type of the bond. The analysis was conducted using VaList

software

[A.S.

Wills and

I.D.

Brown, VaList,

CEA,

France

(1999)],

available from

ftp:Nftp.ill.frlpubldif/valist/.

Crystal structure reJinement 649

the elements themselves, was employed. The calculated bond valence sum

should be as close as possible to the oxidation state for which it was

calculated.

our model, the bond valence sum technique resulted in 2.93 for

the first atom, treated as ~n~', and 1.96 for the second atom, assumed to be

~i~'. The next closest possibility was 2.78 for ~i~' in the first position and

2.61 for

~n~' in the second metal site (see Table

6.37).

Therefore, bond

valence sum clearly reveals that the first metal (Mnl) is actually Mn, while

the second atom (Mn2) is Ni. Furthermore, their oxidation states are 3+ and

2+ for Mn and Ni, respectively. The final chemical composition is, therefore,

N~~+M~~+o*(oH), thus confirming the presence of a hydroxyl group in the

compound.

NiMn03, both Mn and Ni atoms should have oxidation states

3+ to maintain charge balance. Hence, all subsequent refinement steps

included Mn and Ni in proper sites and their atomic displacement parameters

were refined independently.

Including both grain size and strain contributions to the full width at half

maximum (X and

together with their anisotropic parts (X, and Y,)

noticeably improves the fit (Table

7.1

7).

Setting the porosity and absorption

effects using the Suortti approach as free variables (the majority of other

parameters were fixed to avoid correlations) changed the corresponding

parameters from 0.40 and 0.40 to 0.32 and

0.5 1, respectively, without

improvement of the figures of merit. Finally

V, and

parameters, which

represent the instrumental part of the FWHM, were refined until the full

convergence was achieved. The visible improvement of the profile figures of

merit points, perhaps, to the improper preset values of

V, and

We note

also that X and Xa were kept fixed during the last few least squares cycles

because of their strong correlation with

and Ya, and it was nonessential

which pair was refined since we had no intent to analyze grain size

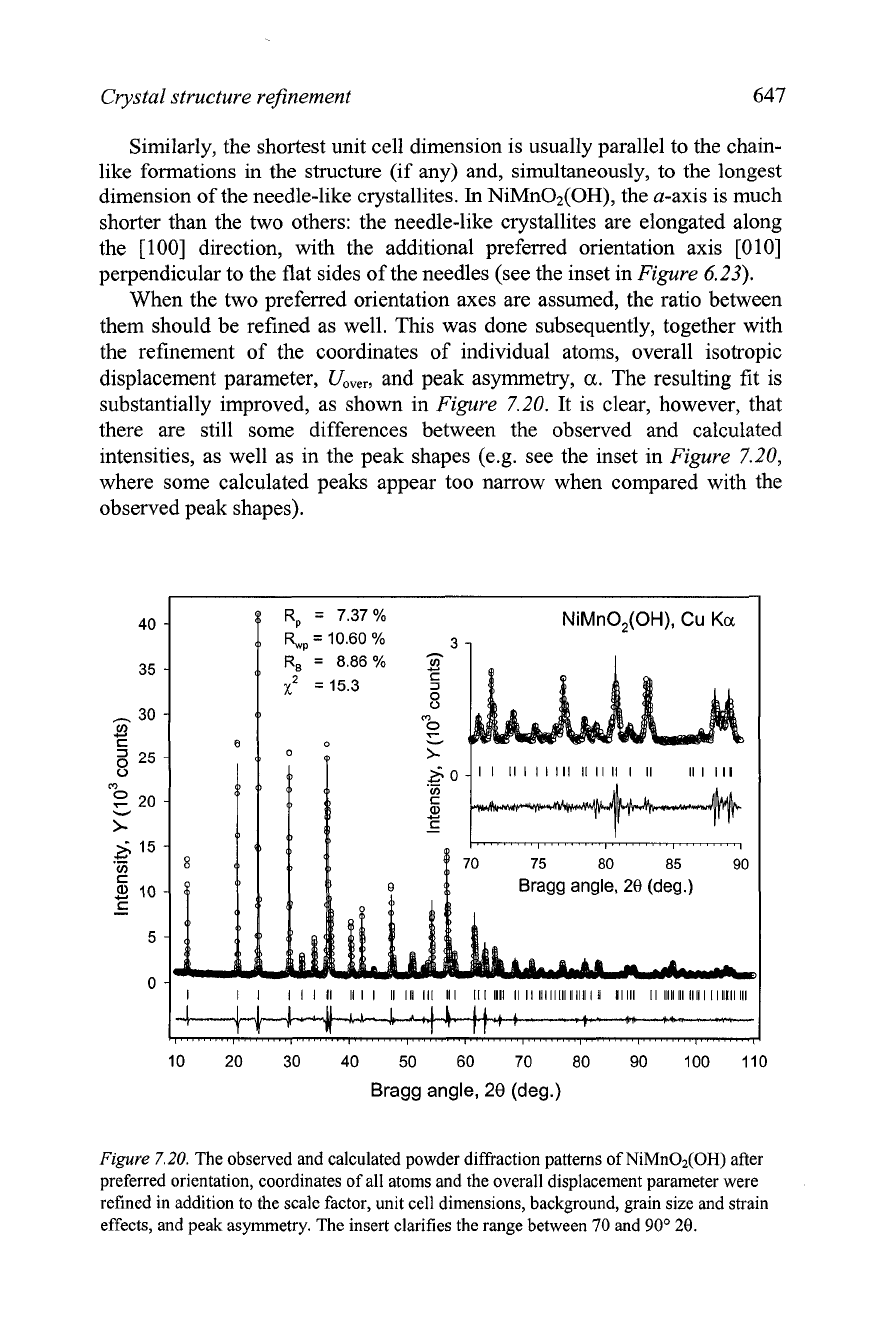
distribution and micro strain effects. The resultant observed and calculated

diffraction patterns are shown in Figure

7.21.

The results of the last refinement can be considered final if the location

of a single independent hydrogen atom in the unit is not of concern.' Not

surprisingly, it was impossible to locate hydrogen from the x-ray data

unambiguously. Therefore, we will also employ neutron powder diffraction

data collected on a powder diffractometer at the McMaster University

nuclear reactor using thermal neutrons with

1.3920

Due to the low x-ray scattering ability of hydrogen atoms, their effect on the intensity of

powder diffraction patterns measured using conventional x-ray sources is usually

negligible, especially in the presence of relatively strongly scattering atoms, such as Mn

and Ni. Therefore, the localization of hydrogen atoms from x-ray powder diffraction data

usually presents a serious and often inexplicable problem. Hydrogen atoms positions are,

however, important in crystallography because they reveal the nature of hydrogen bonds,

which are often critical for understanding the stability of both inorganic and organic

crystals.

650

Chapter

5.08

NiMnO,(OH),

R,,

6.63

0-1

I I1 I I1 Ill I1 llll I I1 Ill Ill

Bragg

angle,

(deg.)

10 20 30 40 50

80 90

100 110

Bragg angle, 28

(deg.)

Figure

7.21.

The observed and calculated powder diffraction patterns of NiMn02(OH) after

the completion of Rietveld refinement using only x-ray powder diffraction data (the hydrogen

atom is still missing from the model). The inset clarifies the range between

and

90"

20.

It is worth noting that a normal sample containing hydrogen, and not its

deuterium-substituted analogue, was employed in this experiment. The

presence of

instead of 2~, causes a substantial diffuse scattering and

significantly increases the background, but on the other hand, it assures that

both the neutron and x-ray diffraction data were collected using exactly the

same compound.

The availability of neutron diffraction data enables the combined x-ray

and neutron Rietveld refinement.' The following neutron scattering lengths

(b) were employed: bM,

-3.73, bNi

10.3, bo

5.803 and bH

-3.739 (all

are in fm).2 The negative values of the scattering lengths of Mn and H can be

used to distinguish them from other elements easily. After several cycles of

the refinement, a good agreement between the observed and calculated

In order to carry out the combined refinement in GSAS, the neutron powder diffraction

pattern

(CD

file Ch7ExOS-Neut.raw) should be added as the second histogram using the

neutron instrumental parameter file (data file Neutron.prm is also located on the

CD).

GSAS employs neutron scattering lengths divided by

10,

i.e. the units are

10-12

cm. Also

note that the incoherent scattering length of

fm, which is quite large.

Crystal structure refinement

patterns was achieved. This result decisively proves that the Mn and Ni

positions were recognized accurately: their scattering factors have opposite

signs and, when switched, the computed intensities will be quite different.

The difference Fourier map was calculated using the neutron data and it

is shown in

Figure

7.22a. The position of an

atom can be found as the

deepest minimum on the map. Yet this minimum is only slightly deeper than

other extremes, all of which could be considered as noise, which appears due

to the relatively low accuracy of the experimental data. The confirmation of

the

position was made by using chemical intuition considering the crystal

structure model, especially because the geometry of the hydrogen bond

01-

H.e.03

is nearly ideal. Positions of all atoms in the model have been

confirmed on the conventional Fourier map, which is shown in

Figure

7.22b.

Figure

7.22.

Distributions of the nuclear density in the unit cell of NiMn02(OH) at

a) the difference Fourier map calculated using IAFI

IFobs-Fcalcl and phase angles calculated

without

atom (pmi,

-2.4

fm/A3, pmax

2.4

fm/A3, Ap

0.4

fm/A3, p(H)

-2.4

fm/A3);

the conventional Fourier map computed using IFob,/ and phase angles calculated including the

atom (pmi,

-12

fm/A3, pmax

fm/A3 (high p on Ni atoms is not shown), Ap

fm/A3,

p(H)

-10

fm/A3, p(Mn)

-12

fm/A3). Solid lines show positive values, thin dotted lines

negative, and thick dotted lines indicate zero level.