Parinov I.A. Microstructure and Properties of High-Temperature Superconductors

Подождите немного. Документ загружается.

28 1 Superconductors and Superconductivity

is the phase transition of II type. Abrikosov found theoretically vortex struc-

tures in superconductors, and thus explained experiments of Shubnikov, who

together with co-authors discovered them as long ago as 1937 by observing

the unusual behavior of some superconductors in external magnetic ﬁeld [948].

Abrikosov assumed that mixed state of superconductor (or Shubnikov phase)

is the vortex state, in which superconducting vortices form periodic lattice [3].

Neither the London nor the Ginzburg–Landau theory could answer the

question: “What are those ‘superconducting electrons,’ whose behavior they

were intended to describe?” It was 46 years since the discovery of supercon-

ductivity, but at the microscopic level a superconductor remained a mystery.

This issue was ﬁnally resolved in 1957 by the work of Bardeen, Cooper and

Schrieﬀer [50], in which the so-called BCS theory was presented. In 1958, an

important contribution was also made by Bogolyubov [73], who developed

mathematical methods which were widely used in studies of superconductiv-

ity. The BCS theory described the process of coupling of the conductivity

electrons with formation of pairs and regrouping into one quantum state. In

contrast to ideal electrons, all pairs could be in the same quantum state, form-

ing macroscopic quantum wave. In these conditions, electric current exists for

account of a motion the all aggregate of paired electrons without scatter-

ing of energy of the single electrons, that is, electric resistance. In the BCS

theory, the formation of pairs is explained by the existence of a certain type

of indirect interactions between electrons. This interaction has a character of

attraction and, therefore, is a contrast to Coulomb force that pushes away

one electron on other. Displacing the conductivity electron in metal during its

motion causes a local deformation of crystalline lattice on account of attraction

forces, with which it acts on positive ions (cations of crystal). This deformation

(one from the types of the lattice excitations) can interact with the second

electron. Due to this process, there is an attraction of two electrons that ren-

der to be “coupled” for account of crystalline lattice. This interaction exists

on account of link of the electrons with quantums of excitations, that is, with

lattice phonons. The formed pairs of electrons are called Cooper pairs.An

existence of interaction “electron–lattice–electron” leads to change of ener-

getic spectrum of electrons. It is known that in the solid the energetic levels

accessible for electrons form consequent zones. Conductor is characterized by

the conductivity zone occupied partially up to the energy of E

, called the

Fermi level. In superconductor the BCS theory predicts at this energy E

the beginning of a restricted zone (energy gap) that separates base state of

system of the coupled electrons from excited states occupied by usual (un-

coupled) electrons. Width, Δ, of this zone is equal to an energy that it is

necessary to apply in order to break the pair and consequently for the failure

of superconductivity. One depends on a temperature, namely has maximum

value at the zero temperature and is equal to zero at the T = T

. In several

cases, superconductivity can exist even in the absence of a restricted zone.

The BCS theory explained directly the isotope eﬀect, discovered in 1950,

and, it was very important to ﬁnd the critical temperature, T

, through phonon

1.5 Theories of Superconductivity 29

and electron characteristics. This opened a possibility to search sensibly new

superconductors with higher T

from materials with great values of Debye

temperature and constant electron–phonon coupling.

In 1959, the microscopic theory of superconductivity was elaborated

further by Gor’kov, who developed a method to solve the BCS problem,

using Green’s functions [327–329]. He applied this method, in particular, to

ﬁnd microscopic interpretations for all phenomenological parameters of the

Ginzburg–Landau theory, as well as to deﬁne the theory’s range of validity.

The works of Gor’kov completed the development of the Ginzburg–Landau–

Abrikosov–Gor’kov theory.

In 1964, Little and Ginzburg expressed independently an idea about proba-

ble non-phonon mechanism of superconductivity in low-dimensional (quasi-1D

or quasi-2D) systems. It was shown that substitution of phonons by excitons

(excitations of sub-system of the coupled electrons) should permit, in princi-

ple, to increase T

up to 50–500K. However, search of these superconductors

was unsuccessful.

The soliton (or bisoliton) model of superconductivity was considered for

the ﬁrst time by Brizhik and Davydov in 1984 [92] in order to explain the

superconductivity in organic quasi-1D conductors discovered by J´erome and

co-authors in 1979 [484].

In 1986, trying to explain the superconductivity in heavy fermions dis-

covered in 1979, Miyake and co-authors considered the mechanism of super-

conductivity based on the exchange of antiferromagnetic spin ﬂuctuations

[708]. The calculations showed that the anisotropic even-parity couplings are

assisted, and the odd-parity as well as the isotropic even-parity are impeded

by antiferromagnetic spin ﬂuctuations.

Interest in the research of superconductivity obtained powerful impulse in

1986 due to the discovery of oxide high-temperature superconductors,

made

by Bednorz and M¨uller. The classical BCS theory was unable to explain many

of their properties. The electron–phonon mechanism became questionable.

By analyzing the layered structure of cuprates, Krezin and Wolf proposed,

in 1987, a model of high-temperature superconductivity based on the existence

In fact, in the early 1970s, a compound of lanthanum and copper oxides was

synthesized in Moscow (USSR). This research was not connected with super-

conductivity, but the researchers were looking for good and cheap conductors.

At low temperatures, the conductivity of this new material showed an abnormal

behavior. The scientists understood the signiﬁcance of this abnormality, but, nev-

ertheless, they could not continue the next experiments because in these years

there were great diﬃculties with liquid helium. Moreover, they did not reveal per-

sistence in defense their questionable results. The mysterious compound was put

away in a cupboard and forgotten. Thus, in 1986, Bednorz and M¨uller discovered

high-temperature superconductivity practically in the same compound that had

been synthesized before in the USSR [846]. So, the possibility of the supercon-

ductivity discovery in cuprates a few years earlier, than in heavy fermions and

organic superconductors, was missed.

30 1 Superconductors and Superconductivity

of two energy gaps, namely superconducting and induced [579, 580]. Indeed,

diﬀerent experiments performed after 1987 have demonstrated the existence

of two gaps; however, they both have the same superconducting origin.

In 1987, Gor’kov and Sokol proposed existence of a new type of microscopic

and dynamical phase separation [330] that was later discovered in other the-

oretical models

In this year, Anderson proposed a model of superconductivity in cuprates,

separating the coupling mechanism and the mechanism for the establishment

of phase coherence [23].

In 1988, Davydov suggested that high-temperature superconductivity

occurs due to the formation of bisolitons, as it takes place in organic supercon-

ductors [178]. In 1990, he presented a HTSC theory based on the concept of

a moderately strong electron–phonon coupling [179, 180]. The theory utilizes

the concept of bisolitons or electron (hole) pairs coupled in a single state due

to local deformation of the –O–Cu–O–Cu– chain in CuO

planes.

In the early 1990s, based on the Anderson’s assumption, namely, that in

cuprates the coupling mechanism and the mechanism for the establishment

of phase coherence are diﬀerent, some theorists autonomously proposed that

independently of the origin of coupling mechanism, spin ﬂuctuations cause

the long-range phase coherence in cuprates.

In 1994, Alexandrov and Mott showed that, in cuprates, it was neces-

sary to distinguish the “internal” wave function of a Cooper pair and the

order parameter of the Bose-Einstein condensate, which may have various

symmetries [13].

In 1995, Emery and Kivelson emphasized that superconductivity requires

coupling and long-range phase coherence [249]. They demonstrated that in

cuprates, the coupling can occur above T

without the phase coherence.

In the same year, Tranquada et al. found the presence of coupled, dynam-

ical modulations of charges (holes) and spins in Nd-doped La

2−x

CuO

(LSCO) by using neutron diﬀraction [1076].

In 1997, Emery, Kivelson and Zachar presented a theoretical model of

HTSC based on the presence of charge stripes in CuO

planes [250].

In 1998, Chakraverty et al. attempted to prove that the theory of bi-polaron

superconductivity of HTSC contradicted with experiments and was theoreti-

cally discrepant [134]. In answer of Alexandrov [11], was been stated contrary

opinion, namely: the negation of the bi-polaron superconductivity of HTSC is

the result erroneous approximation for energetic spectrum of bi-polarons and

erroneous application of the bi-polaron theory carried out by Chakraverty

et al. Based on two-zone model, he obtained a formula for T

,whichwasfree

from adjusted parameters and included besides basic constants the concentra-

tion of carriers, n, and penetration depths of magnetic ﬂux λ

and λ

along

two mutually perpendicular crystallographic directions. The substitution of

test values of n, λ

and λ

(for Y-123) estimated T

∼ 100 K. It proves self-

consistency of the bi-polaron approach and testiﬁes HTSC to be in the regime

of Bose–Einstein condensation.

1.5 Theories of Superconductivity 31

In 1999, analysis of tunneling and neutron scattering measurements, car-

ried out by Mourachkine, showed that in Bi

CaCu

8+x

(Bi-2212) and

YBa

6+x

(YBCO), the phase coherence is established due to spin

excitations [732, 733], which cause the appearance of the so-called magnetic

resonance peak in inelastic neutron scattering spectra [899].

In this year, Cronstrom and Noga determined a new solution of BCS equa-

tions in approximation of mean ﬁeld, which pointed to the existence in thin

superconducting ﬁlms (or in superconducting bulks with layered structure)

of type-III phase transitions [167]. The critical temperature of this transition

increases at decreasing of the layer thickness and is independent of isotope

mass. The electronic heat capacity is a continuous function of temperature,

but has discontinuity of derivative.

In 1999, Leggett deﬁned a very simple dependence, T

(n) for “calcium”

HTSC (where n is the number of CuO

layers per elementary cell): T

(n)=

(1)+T

(1−1/n), where T

is the own constant for each Bi, Hg and Tl family,

in which the CuO

layers are separated by calcium layers [615]. In particular,

it is followed from this formula that [T

(3) − T

(2)]/[T

(2) − T

(1)] = 1/3,

which agrees with test data 0.25–0.28 and 0.25–0.34 for HTSC on the basis

of Hg and Tl, respectively.

In 2000, Tang measured the critical temperature, T

,ofultra-thinHTSC

ﬁlms YBa

depending on their thickness d. It has been observed

approximately linearly on d a diminishing of T

with decreasing of the ﬁlm

thickness at d<10 nm [1046]. The dependence T

(d) is well described by the

empirical formula: T

= T

(1 − d

/d), where T

=90Kandd

=1.56 nm.

The critical thickness, d

, is near to the thickness of one elementary cell along

c-axis that supports quasi-2D nature of HTSC superconductivity.

In 2001, Kivelson proposed the following way for increasing of T

: it is nec-

essary to create multi-layer systems with diﬀerent concentrations of carriers

in various layers, so the layers with low concentration of carriers provide their

coupling, but the layers with high concentration of carriers guarantee phase

rigidity [553]. Maximal critical temperature of HTSC is found by competition

of two eﬀects: (i) the coupling interaction weakens at increasing of the charge

carrier concentration, x, that is connected with properties of doped Mott’s

dielectric, but (ii) the density of super-ﬂuid component, which controls the

system rigidity in relation to phase ﬂuctuations, increases with growth of x.

Thus, optimal T

is reached at the boundary of the region with prevalence of

the phase alignment and region with prevalence of the coupling interaction.

In the same year, based on tunneling measurements, Mourachkine provided

evidence that the quasiparticle peaks in tunneling spectra of Bi-2212 crystals

are caused by condensed soliton-like excitations, which form the Cooper pairs

[734–736].

In 2002, Cui proposed a possible responsibility for superconductivity of

relativistic attraction of electrons. At least, there are two types of collective

movement in superconductors, which can suppress usual Coulomb repulsion of

electrons as the attraction component becomes predominant. This movement

32 1 Superconductors and Superconductivity

is caused by combination of electron gas and phonons in conventional super-

conductors and by itself electron gas (or electron liquid) – in HTSC. The re-

pulsion and attraction between electrons balance approximately each other in

majority of matters; therefore, the theory of electron gas (i.e., non-interacting

particles) works well. However, the repulsion predominates over attraction in

some matters, and then electron sub-system demonstrates properties directly

contrary to superconductivity [168].

In this year, Laughlin showed that cuprate HTSC in undoped state should

be considered as no dielectrics, but superconductors with very great gap and

extremely small super-ﬂuid density [605]. Laughlin named these superconduc-

tors “gossamer superconductors.” In practice, a brittleness of coupled state

of this superconductor creates obstacles for stating superconductivity in all

volumes. However, he assumed that the wave function of this coupled state

can serve as a good starting point for understanding of correlations between

Mott’s dielectric and HTSC.

In 2003, Hussey et al. proved an existence of 3D Fermi surface, based on

investigations of angle oscillations of magnetic resistance in HTSC Tl

CuO

6+δ

[459]. Thus, almost a 20-year-old argument about coherency or inco-

herency of electronic states along the c-axis was solved in favor of coherency.

In 2004, Homes et al. obtained the next universal scaling relationship

between physical values, characterizing normal and superconducting states

of HTSC [435]: ρ

= As

(where ρ

is the density of super-ﬂuid compo-

nent, s

is the static speciﬁc conductivity and T

is the critical temperature),

which should be carried out for all HTSC, without dependence on the value of

, type of carriers (holes or electrons), doping level, crystalline structure and

current direction (parallel or perpendicular to CuO

planes). In this case, the

proportionality factor, A = 120 ±25, if ρ

is measured in s

−2

in (Ω cm)

−1

and T

in K. The straight dependence, ρ

), includes even the points

for low-temperature superconductors Pb and Nb. It covers diapason above

of ﬁve degree of magnitude on each of the coordinate axes. This empirical

dependence is surprising, if taking into account the principally diﬀerent char-

acter of current transfer in various crystallographic directions (i.e., coherent

in ab-plane and incoherent along c-axis).

In this year, Alexandrov again explained HTSC physics on the basis

of bi-polarons mechanism. HTSC properties weakly diﬀer from usual met-

als, namely: there is standard BCS phenomenon, only Bogolyubov’s quasi-

particles (Cooper’s pairs with d-symmetry) transfer current. The magnetic

mechanism of superconductivity exists, but as subsequent of electron–phonon

coupling. Because constants of electron–phonon coupling are greater than 1,

polarons and super-light bi-polarons must arise. In this case, the critical tem-

perature is found as [12]

=1.64[eR

/(λ

)

(λ

)

]

1/3

, (1.14)

where e is electron charge, R

is Hall constant, λ

and λ

are the penetration

depth of magnetic ﬁeld in ab-plane and along c-axis, respectively.

1.6 High-Temperature Superconductors 33

In 2006, Honma and Hor proposed to distinguish 2D and 3D hole con-

centration [436]. It is well known that the critical temperature of HTSC is a

universal function of this parameter (the hole concentration is usually found

by number of holes per Cu atom in CuO

layer). Their analysis shows that T

is deﬁned by 3D concentration, n

, and universal bell-like dependence takes

place just for T

In this year, Terashima et al. demonstrated experimentally in HTSC a

change of character of the anomaly for the law of electron dispersion (so-called

“kink”) in the vicinity of Fermi level at partial substitution of Cu atoms by

Zn and Ni atoms, not much diﬀering in mass, but in other spin states (that

may be considered as “magnetic isotope-eﬀect”) [1052].

Obviously, the above list of mechanisms and superconductivity theories

is not complete. Finally note that beginning from 1987, theorists proposed

more than 100 models of high-temperature superconductivity, in particu-

lar, based on the representations about polarons, plasmons, excitons, soli-

tons, super-exchange and direct interaction between electrons. Today, the

intensive discussion of HTSC mechanisms and high critical temperatures,

, to being proper for these materials is continued. Some review results

of diﬀerent HTSC theories can be found in the overviews and monographs

[99,172,299,452,666,737,986].

1.6 High-Temperature Superconductors

1.6.1 General Remarks on Type-II Superconductors

High-temperature superconductors placed in the center of our research are the

type-II superconductors. Therefore, their properties and superconductivity

mechanisms are considered in more detail. The term type-II superconductors

was ﬁrst introduced by Abrikosov in his classical paper [3], where he assumed

a detailed phenomenological theory of these materials’ behavior, based on

the Ginzburg–Landau theory, and explained their magnetic properties. Ini-

tially, Abrikosov’s theory was greeted with certain skepticism: so much out

of the ordinary was in its predictions. However, at the next development of

physics of superconductors this theory obtained numerous experimental sup-

ports. Finally, several years later it was accepted in total, when it consequently

explained the complex behavior of superconducting alloys and compounds, in

particular the very high critical ﬁelds of some materials. As has been noted

for type-II superconductors, the energy of an interface between a normal and

a superconducting region σ

< 0. Total displacement of external ﬁeld from

superconductor does not lead to a state with the least energy, if the con-

tribution of surface energy of the interface between two phases is signiﬁcant.

Therefore, in this case, the energetically favorable state is that at which super-

conductor of corresponding shape (any one, besides an inﬁnitely long cylinder

34 1 Superconductors and Superconductivity

placed in a parallel magnetic ﬁeld) is divided into great number of alternating

superconducting and normal regions.

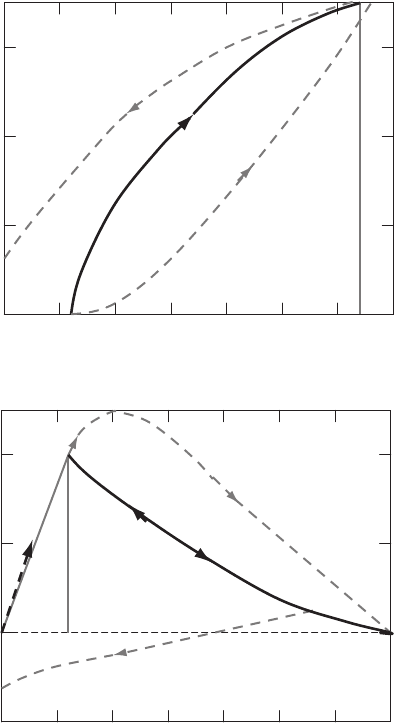
The magnetization curve of a type-II superconductor in the form of a long

cylinder, placed in a parallel magnetic ﬁeld, is shown schematically in Fig. 1.9.

As long as the external ﬁeld is H<H

, the ﬁeld in the interior of the sample

is absent (B =0).However,atH

<H<H

, a steadily increasing ﬁeld

penetrates the superconductor in the form of ﬂux lines (vortices). It remains

below the external ﬁeld H, and superconductivity of the sample is not de-

stroyed. At a certain ﬁeld H = H

, the ﬁeld in the interior becomes equal

to external ﬁeld H, and the bulk superconductivity disappears. In contrast

to the type-I superconductors, the superconductivity may easily originate in

a heterogeneous way in these materials. In this case, the ﬁeld of the super-

conductivity initiation H

maybewellabovethecriticalthermodynamic

ﬁeld H

. Between H

and H

, the material has no electric resistance and

contains a lattice of ﬂux lines, which can be simplistically treated as normal

regions. This is the mixed state, also known as the Shubnikov phase [987].

In dirty materials (with defects) vortices remain anchored onto impurities,

leading to signiﬁcant hysteresis and even paramagnetization curves, as shown

in Fig. 1.9.

Thus, the above H

type-II superconductors do not show the Meissner

eﬀect. Magnetic ﬁeld penetrates into these materials in the form of quantized

ﬂux lines (vortices), each of which has a normal core, which can be approxi-

mated by a long thin cylinder with its axis parallel to the external magnetic

ﬁeld. Inside the cylinder, the order parameter, Ψ = 0. The radius of the cylin-

der is of the order ξ, the coherence length. The direction of the super-current,

circulating around the normal core, is such that the direction of the magnetic

ﬁeld, generated by it, coincides with that of the external ﬁeld and is parallel

to the normal core. By this, the vortex current circulates into region with

radius of the order λ. The size of this region is by far above a value ξ, because

λ>>ξfor type-II superconductors [935].

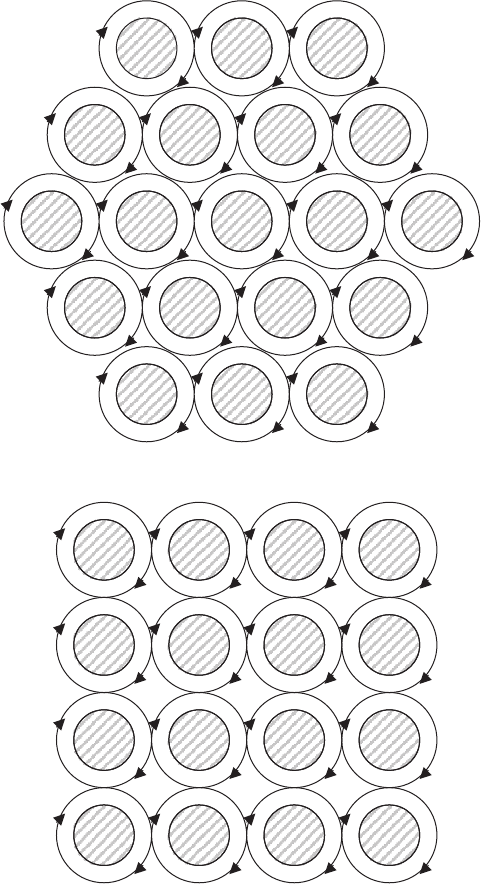
Each vortex carries one magnetic ﬂux quantum. Penetration of vortices in

the interior of a superconductor becomes thermodynamically favorable at H>

. Inside the superconductor, the vortices arrange themselves at distances

∼λ, from each other, so that in the cross-section, they form a regular triangular

or square lattice (see Fig. 1.10). This state of superconductor (at H

<H<

) is the mixed state, because it is characterized by a partial penetration

of the magnetic ﬁeld in the interior of the sample. Once formed at H

,the

vortex lattice persists at much higher ﬁelds. As the external ﬁeld increases, the

lattice period steadily decreases and the density of the vortices rises. Finally,

at a ﬁeld H = H

, the vortex lattice becomes so dense that the distance

between the neighboring vortices, that is, the lattice period attains the order

ξ. This means that the normal cores of the vortices come into contact with

each other and the order parameter Ψ becomes zero over the total volume of

the superconductor, that is, a second-order phase transition occurs.

1.6 High-Temperature Superconductors 35

1.5

1.0

0.5

0.0

0.5 1.0 1.5

1.0

0.5

0.0

–

0.5

0.0 0.5

1.0 1.5

H / H

–M / H

B / H

(a)

(b)

Fig. 1.9. Magnetic induction (a) and magnetization (b) as a function of applied

ﬁeld in type-II superconductors. Dotted lines correspond to impure samples [617]

1.6.2 Doping of Cuprates

The simplest copper oxide perovskites are insulators. In order to become

superconducting, they should be doped by charge carriers. There are two

ways to increase the number of charge carriers in cuprates chemically: (i) to

substitute metallic atoms in the intermediate planes by higher-valence atoms

and/or (ii) to change the number of oxygen atoms. Doping increases the num-

ber electrons or holes at the Fermi level. The concentration of charge carriers

36 1 Superconductors and Superconductivity

(a)

(b)

Fig. 1.10. Mixed state of a type-II superconductor. Superconducting vortices form

a regular triangular (hexagonal) (a)orsquare(b) lattice. Vortex cores (dashed

regions) are normal

in HTSC is low (∼5×10

), in comparison with conventional superconductors

(∼5×10

−10

). However, due to the large coherence length in conventional

superconductors, only a 10

−4

part of the electrons, located near the Fermi

1.6 High-Temperature Superconductors 37

surface, participate in coupling. At the same time, in cuprates, ∼ 10% of all

conduction electrons (holes) form the Cooper pairs.

In conventional superconductors, the critical temperature increases mono-

tonically with growth of charge carriers: T

(p) ∝ p. In cuprates, this depen-

dence is non-monotonic. In most of hole-doped cuprates, (but not in all) the

(p) dependence has the bell-like shape and can be approximated as [866]

(p)

∼

c,max

[1 − 82.6(p − 0.16)

] , (1.15)

where T

c,max

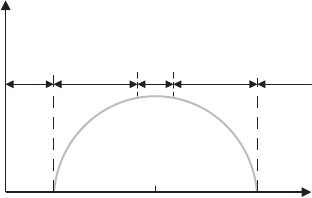
is the maximum critical temperature for a given compound.

Superconductivity occurs within the limits, 0.05 ≤ p ≤ 0.27, which vary

slightly in various cuprates. Thus, the diﬀerent doping regions of the super-

conducting phase may be chosen such as the underdoped, optimally doped and

overdoped regions (Fig. 1.11). The insulating phase at p<0.05 is called the

undoped region, but above 0.27, cuprates become metallic.

The ratio between the maximum critical temperatures in hole-doped and

electron-doped cuprates is 135 K/24K=5.6. Obviously, it may be assumed

that the electron–hole asymmetry has fundamental character: superconduct-

ing hole-doped compounds will always have the critical temperature a few

times higher than the same electron-doped superconductor.

In cuprates and in many other compounds with low dimensionality, the

distribution of charge carriers is inhomogeneous. Moreover, in cuprates, this

distribution is inhomogeneous in a micro-, as in a macroscopic scale (Fig. 1.12).

In the undoped region (p<0.05), doping holes are preferably distributed

inhomogeneously into CuO

planes, and they form dynamical 1D charge

strips (so-called charge-strip phase). In the undoped region, these strips have

diagonal shapes and locate not along–O–Cu–O–Cu–bonds, but along the

diagonal–Cu–Cu–Cu–direction, as shown in Fig. 1.12. In undoped cuprates,

the concentration of holes is low, but the distance between charge strips, sep-

arated by 2D insulating antiferromagnetic domains, is large. The charge-strip

0 0.05 0.16 0.27

12 4 5

Fig. 1.11. Critical temperature as a function of doping [737]. Numbers mark the

next regions: 1, undoped (p<0.05); 2, underdoped (0.05 ≤ p ≤ 0.14); 3, optimally

doped (0.14 <p<0.18); 4, overdoped (0.18 ≤ p ≤ 0.27); and 5, metallic phase

(p>0.27)