Parinov I.A. Microstructure and Properties of High-Temperature Superconductors

Подождите немного. Документ загружается.

18 1 Superconductors and Superconductivity

dc-component V , the voltage will also have an ac-component of angular

frequency ω,sothat

ω =2eV , (1.2)

where  is Planck’s constant and e is the electron charge.

1.3.3 The Meissner Eﬀect

Not only is the superconductivity phenomenon a state of zero resistance, but

a superconductor is not simply an ideal conductor to being a piece of metal

with zero resistance. Consider the behavior of an ideal conductor in an external

magnetic ﬁeld that is weak enough so as not to destroy the specimen’s ideal

conductivity. Suppose that initially the ideal conductor is cooled down below

the critical temperature in zero external magnetic ﬁeld. After that an external

ﬁeld is applied. From general considerations, it is easy to show that the ﬁeld

does not penetrate the interior of the sample (Fig. 1.6). Let us prove this with

the help of Maxwell’s equations. As the induction B changes, an electric ﬁeld

E must be induced in the specimen due to the equation

curlE = −c

−1

∂B/∂t , (1.3)

where c is the speed of light in vacuum.

In the ideal conductor E =0,since

E = jρ, (1.4)

where ρ is the resistivity (which in our case is zero) and j is the density of the

induced current.

It follows that B = const and taking into account that B =0before

applying the external ﬁeld, we arrive at B = 0 in any point of the ideal

(a) (b)

Fig. 1.6. Dependence of magnetic state of an ideal conductor on its history at

T<T

and H>0: (a) magnetic ﬁeld applied to an ideal conductor at T<T

;

(b) ﬁeld applied at T>T

1.3 Superconductivity Phenomena 19

conductor also after the ﬁeld is applied. However, the same situation (an

ideal conductor at T<T

in an external magnetic ﬁeld) can be reached

through another sequence of events, that is, by ﬁrst applying the external

ﬁeld to a “warm” sample and then cooling it down to T<T

.Inthatcase,

electrodynamics predicts an entirely diﬀerent result. At T>T

, the resistivity

of the sample is ﬁnite and, therefore, the magnetic ﬁeld penetrates into it.

After cooling the specimen down through the superconducting transition, the

ﬁeld remains in it (see Fig. 1.6b).

The experiment by Meissner and Ochsenfeld [693] showed that the su-

perconductor is not only an ideal conductor. They revealed that at T<T

the ﬁeld inside a superconducting specimen was always zero (B =0)inthe

presence of an external ﬁeld, independent of which a procedure has been cho-

sen to cool the superconductor below T

. Therefore, the superconductor is

the perfect diamagnetic having negative magnetic susceptibility (i.e., ratio of

magnetization to magnetic ﬁeld) and stating zero ﬁeld inside itself.

So, if condition B = 0 is independent of the specimen’s history, the zero

induction can be treated as an intrinsic property of the superconducting state

at H<H

. Furthermore, it implies that we can treat a transition to the

superconducting state as a phase transition, but the superconducting state

obeys the equations

ρ =0, (1.5)

B =0. (1.6)

1.3.4 The Isotope Eﬀect

The isotope eﬀect provided a crucial key to the development of the supercon-

ductivity theory of Bardeen–Cooper–Schrieﬀer (BCS) discussed in Sect. 1.5.

It was found that for a given element, T

was proportional to M

−1/2

,where

M is the isotope mass. The vibration frequency of a mass M on a spring

is proportional to M

−1/2

. The same relation holds for the characteristic vi-

bration frequencies of the atoms in a crystal lattice. So, the existence of the

isotope eﬀect indicated that although superconductivity is an electronic phe-

nomenon, it is nevertheless connected with the vibrations of the crystal lattice

in which the electrons move. However, after the development of the BCS the-

ory, for some conventional (i.e., obeying the BCS theory) superconductors,

the exponent of M is not − 1/2, but near zero (see Table 1.4).

Table 1.4. Isotope eﬀect (T

∝ M

−α

) [581]

Element Mg Sn Re Mo Os Ru Zr

α 0.5 0.46 0.4 0.33 0.21 0 (±0.05) 0 (±0.05)

20 1 Superconductors and Superconductivity

In high-temperature superconductors, the exponent is also near zero. This

fact caused research of HTSC mechanisms that are distinct on the electron–

phonon interactions.

1.3.5 Penetration Depth and Coherence Length

Detailed studies have shown that provided the magnetic ﬁeld remains weak

enough, it gradually diminishes at the superconductor surface over a depth

λ of some hundreds of angstroms order. This is called the penetration depth.

When an external magnetic ﬁeld is applied, a direct thermodynamic current

appears at the superconductor surface in such a way as to screen the bulk

from the applied ﬁeld. The phenomenological theory of superconductivity,

proposed by Gorter and Casimir and based on the assumption that there

are two components of conducting electronic “ﬂuid” in superconducting state,

namely “normal” and “superconducting,” gave the name two-ﬂuid model [326].

The properties of the “normal” component are identical to system of electrons

in the normal metal, but the “superconducting” component is responsible

for the anomalous properties. In the framework of the two-ﬂuid model of

superconductor, the temperature dependence of the penetration depth λ is

approximated well by [325]

λ(T )=

λ(0)

[1 − (T/T

)

]

1/2

. (1.7)

The divergence of λ at transition (T → T

) shows that we pass continu-

ously from the normal metal, in which λ = ∞, to the superconducting state

(see Fig. 1.5b). In non-zero ﬁeld, λ varies discontinuously from λ = ∞ to a

ﬁnite value, and the transition is then ﬁrst order.

Taking into account sharpness of the superconducting transition at the

absence of magnetic ﬁeld and also signiﬁcant dependence of the observed

depth λ on the admixture concentration, Pippard concluded that supercon-

ducting state should be characterized by a ﬁnite coherency length of electron

impulse (Δp) [847], but no inﬁnite one as in the theory of the brothers F.

and H. London [644]. Therefore, the order parameter changes smoothly at

the distance ξ, called the coherence length. Based on the estimation made by

Pippard for dependence λ on the ﬁeld, the length of ξ ∼ 1 μm. The coherence

length is the distance between two electrons of Cooper pair, to be in essence

space characteristic of superconducting electrons, on which value it could be

judged by using the relation of uncertainties

ξ ≈



Δp

≈

ν

, (1.8)

where ν

is Fermi velocity and k is Kelvin constant.

To explain the dependence of depth λ on the length of the free run of elec-

trons l, Pippard proposed that an eﬀective coherence length ξ(l) is connected

1.4 Magnetic Properties of Superconductors 21

with corresponding value of ξ

for pure metal by the equation

ξ(l)

, (1.9)

where A is the constant near unit.

In the two limit cases, the evident equations for λ may be obtained in the

form:

λ = λ



ξ(l)



1/2

at ξ<<λ(London limit) , (1.10)

where



4πn



1/2

is the London penetration depth; m and e are the mass and charge of electron,

respectively; n

is the quantitative density of superconducting electrons.

The condition ξ<<λis carried out for pure metals near T

(where λ →∞)

and also for alloys and thin admixture ﬁlms, where l and ξ are decreased or

limited by the electronic scattering at defects, admixtures or at ﬁlm bound-

aries, so that ξ → l at l → 0. The contrast limit case (ξ>>l), corresponding

to most part of bulk superconductors (l →∞), at the temperatures leads to

far from T

l→∞



√

2π



1/2

at ξ>>λ(Pippard limit) . (1.11)

1.4 Magnetic Properties of Superconductors

According to their magnetic properties, superconductors are divided into

type-I superconductors and type-II superconductors. Type-I superconductors

include all superconducting elements except niobium. Niobium, superconduct-

ing alloys and chemical compounds are type-II superconductors. The high-

temperature superconductors also belong to this group. The main diﬀerence

between the superconductors of both types lies in their diﬀerent response to

an external magnetic ﬁeld. The Meissner eﬀect is observed in type-I super-

conductors, only.

1.4.1 Magnetic Properties of Type-I Superconductors

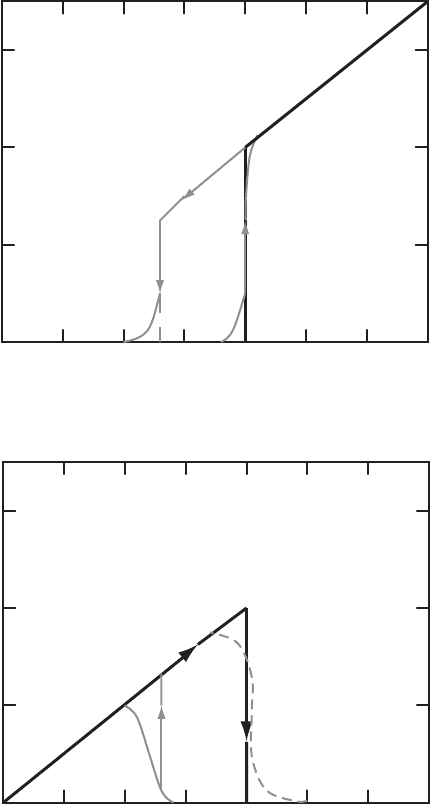
Let us consider the magnetization curve of a superconductor representing a

long cylinder in a longitudinal external magnetic ﬁeld H. When the ﬁeld H

increases, the induction inside the sample does not change at ﬁrst; it remains

at B =0.AssoonasH reaches the value of H

, the superconductivity is

destroyed, the ﬁeld penetrates into the superconductor and B = H. Therefore,

22 1 Superconductors and Superconductivity

the magnetization curve B = B(H) has the form shown in Fig. 1.7a. The

magnetic induction B and magnetic ﬁeld H are related to each other by the

expression:

B = H +4πM , (1.12)

where M is the magnetic moment per unit volume (Fig. 1.7b).

In type-I superconductors, the diamagnetism (i.e., negative value of mag-

netic moment and its contrast direction to magnetic induction vector) remains

up to the value of ﬁeld H

. This supercooling of normal phase is caused by

the diﬃculty of local nucleating a superconducting region within a normal re-

gion in type-I superconductors. If there are defects (e.g., dislocations) in the

crystal lattice, these can modify such theoretical behavior by smoothing out

transitions. Main magnetic properties of type-I superconductors are led from

the (1.5) and (1.6) [594]:

(1) Magnetic ﬁeld lines outside a superconductor are always tangential to its

surface. Indeed, it is known from electrodynamics that magnetic ﬁeld lines

(i.e., lines of the magnetic induction) are continuous and closed. This can

be written as the equation div B = 0. Then, the components of B that

are normal to the surface must be equal on both sides of the surface, that

is, inside and outside of the sample. However, the ﬁeld in the interior of a

superconductor is absent and, consequently, B

(i)

= 0. It follows that the

normal component B

(e)

at the outside of the superconductor’s surface is

zero, too: B

(e)

= 0, that is, the magnetic ﬁeld lines are tangential to the

surface of the superconductor.

(2) A superconductor in an external magnetic ﬁeld always carries an elec-

tric current near its surface. This is one of the consequences of the ﬁrst

property, because from Maxwell’s equation curl B =(4π/c)j and the

requirement B = 0, it follows that the volume current in the interior of

the superconductor is zero (j = 0) and only a surface current is possible.

Then, from relation between the surface current j

and the magnetic ﬁeld

at the surface of the superconductor H

=(c/4π)(n × H) , (1.13)

where n is the unit vector along the normal to the surface, it is obvious

that the surface current is completely deﬁned by the magnetic ﬁeld at the

surface of a superconductor. In other words, the surface current assumes a

value such that the magnetic ﬁeld generated by it inside a superconductor

is exactly equal in value and opposite in direction to the external ﬁeld.

This assures zero total ﬁeld in the interior: B =0.

(3) In a simply connected superconductor (i.e., body inside of which an arbi-

trary closed path can be reduced to a point without crossing the boundaries

of the body), surface currents can exist only when the superconductor is

placed in an external magnetic ﬁeld. Indeed, if the surface current remains

after switching oﬀ the external ﬁeld, it would create its own ﬁeld in the

superconductor, which is impossible.

1.4 Magnetic Properties of Superconductors 23

1.5

1.0

0.5

0.0

0.0 0.5 1.0 1.5

H / H

B / H

1.5

1.0

0.5

0.0

0.0 0.5 1.0 1.5

–M / H

(a)

(b)

Fig. 1.7. Magnetic induction (a) and magnetization (b), as a function of applied

ﬁeld in type-I superconductors. When the magnetic ﬁeld is reduced, superconductiv-

ity reappears at a ﬁeld H

. Dotted lines correspond to impure samples [617]

24 1 Superconductors and Superconductivity

1.4.2 The Intermediate State

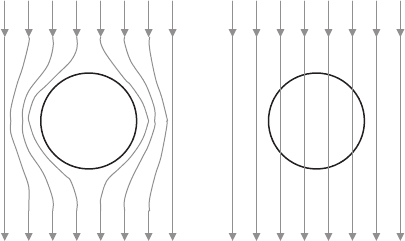
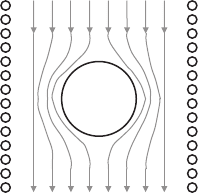
Consider the behavior of a superconducting sphere, placed in an external

magnetic ﬁeld (Fig. 1.8). Since the magnetic ﬁeld lines are always tangential

to the surface of a superconductor, then in this case, it is obvious that the

ﬁeld lines have a higher density at the equator thereby producing a local

increase of the magnetic ﬁeld. At the same time, the ﬁeld at the poles is

absent. Far away from the sphere, where any perturbations are averaged,

the uniform external ﬁeld H is lower than that at the equator. Therefore,

an attainment of the ﬁeld at the equator of the critical value of H

the

magnitude of H<H

and it is not permitted for the whole sphere to revert

to the normal state. On the other hand, it is not permitted for the whole

sphere to be superconducting either, because the ﬁeld at the equator has

already reached the critical value. This contradiction involves a co-existence

of alternating superconducting and normal regions within the sphere, which is

called the intermediate state. The interfaces between these regions are always

parallel to the external ﬁeld, while in the cross-section perpendicular to the

ﬁeld they may assume various intricate conﬁgurations.

Assume that before a superconducting body goes into the intermediate

state, the maximum ﬁeld at its surface (in the case of a sphere, at the equator)

is H

, and the external ﬁeld far away from the body is H. Then, it is obvious

that, on the one hand, H

>Hand, on the other hand, H

is proportional to

H with the proportionality factor dependent on the exact shape of the body. It

canbewrittenintheformH

= H/(1 −n). The values of the demagnetizing

factor n for diﬀerent forms are present in Table 1.5.

With the help of Table 1.5, it is possible to calculate the ﬁeld H correspond-

ing to the transition into the intermediate state for a body of a certain shape.

The transition takes place when the ﬁeld H

reaches the value of H

.Inpar-

ticular, for a sphere it occurs at the external ﬁeld H = H

(1−1/3) = 2/3H

Let us now consider the conditions for thermodynamic equilibrium in the

intermediate state. Assume that the ﬁeld in one of the normal regions exceeds

. Then it must destroy the superconductivity of the adjacent supercon-

ducting regions. Conversely, if the ﬁeld in a normal region is less than H

Fig. 1.8. Superconducting sphere in the homogeneous ﬁeld of a solenoid. Numbers

denote winding of the solenoid (1) and superconducting sphere (2)

1.4 Magnetic Properties of Superconductors 25

Table 1.5. The demagnetizing factor for diﬀerent forms of superconductor

Sample

geometry

Cylinder in

parallel ﬁeld

Cylinder in

transverse ﬁeld

Sphere Thin plate in

perpendicular ﬁeld

n 0 1/2 1/3 1

this region must be superconducting. Therefore, a stable co-existence of the

normal and superconducting regions is only possible, if the ﬁeld in the normal

regions equals to H

1.4.3 Magnetic Properties of Type-II Superconductors

In contrast to type-I superconductors, type-II superconductors do not show

Meissner eﬀect and are characterized by the mixed state, but no intermediate

state. In this case, electric resistance is absent, but a magnetic ﬁeld pene-

trates into superconductor in a quite extraordinary way. Let us consider a

type-II superconductor in the form of a long cylinder placed in a longitudi-

nal magnetic ﬁeld, which is increased from zero. First, the cylinder pushes

out all ﬁeld, causing the zero magnetic induction in the interior of the cylin-

der. This means that the Meissner eﬀect is observed at this stage. However,

beginning from a certain value of the ﬁeld, there is a non-zero (i.e., ﬁnite) in-

duction in the cylinder. This ﬁeld is called the lower critical ﬁeld and denoted

by H

. With next increase of the external ﬁeld H, the induction will build

up until the average ﬁeld in the cylinder becomes equal to the external ﬁeld

H, but the cylinder itself goes to the normal state. This will happen at the

so-called upper critical ﬁeld H

. In 1963, Saint-James and de Gennes have

shown that the superconductivity will remain even at H>H

in a thin

surface layer, until H ≤ 2.392kH

,wherek is Ginzburg–Landau parameter,

is the thermodynamic critical ﬁeld, that is, H ≤ 1.695H

[907]. This ﬁeld

H =1.695H

, also destroying superconductivity in the surface layer has been

named by the third critical ﬁeld and denoted by H

. However, based on the

measurements of magnetic susceptibility of the Nb cylinders under ﬁelds above

[129, 570], it has been stated that the ratio of H

depends on pro-

cessing method of surface, but was above the theoretical value of 1.695 [907]

in all cases. The near-surface critical current was absent in the ﬁelds above

(T )=0.81H

(T ), where factor 0.81 was independent of the temperature,

surface quality and admixtures. The last two parameters led to alteration of

the ratio H

from 1.86 to 2.57. It could be assumed [129, 570] that below

down to H

there is only local near-surface superconductivity in the form

of separate sites, which contribute to the magnetic susceptibility, but do not

provide surface critical current. They couple together only in the ﬁeld below

and a single coherent superconducting state forms.

26 1 Superconductors and Superconductivity

1.5 Theories of Superconductivity

The ﬁrst theory which had success in describing the electrodynamics of super-

conductors, was the phenomenological theory of brothers F. and H. London

(1935). It had introduced two equations, in addition to Maxwell’s ones, gov-

erning the electromagnetic ﬁeld in a superconductor [644]. These equations

provided a correct description of the two basic properties of superconduc-

tors: absolute diamagnetism and zero resistance to a dc-current. The London

theory did not resolve the microscopic mechanism of superconductivity on

the level of electrons. Therefore, the question: “Why does a superconductor

behave according to the London equations?” remained beyond its scope.

According to the London theory, electrons in a superconductor may be

considered as a mixture of superconducting and normal electrons. The quan-

titative density of the superconducting electrons, n

, decreases with increasing

of temperature and attains zero at T = T

. On other hand, at T =0thevalue

of n

is equal to the total density of conductivity electrons. This postulates

two-ﬂuid model of superconductor proposed by Gorter and Casimir. A ﬂux of

superconducting electrons meets no resistance. Obviously, such a current can-

not generate a constant electric ﬁeld in a superconductor because, if it did, it

would cause the superconducting electrons to accelerate inﬁnitely. Therefore,

under stationary conditions, corresponding to absence of an electric ﬁeld, the

normal electrons are at rest. In contrast, in the presence of an ac-electric ﬁeld,

both the normal and the superconducting components of the current are ﬁnite

and the normal current obeys Ohm’s law.

The London equations provided a description for the behavior of the super-

conducting component of the electronic ﬂuid in both dc- and ac-electromagnetic

ﬁeld. They also helped to understand a number of aspects of the supercon-

ductors’ behavior in total. However, by the end of the 1940, it was clear that

one question at least was not answered in the framework of the London the-

ory. For the interfaces between adjacent normal and superconducting regions,

the theory predicted a negative surface energy: σ

< 0. This implied that a

superconductor in an external magnetic ﬁeld could decrease its total energy

by turning into a mixture of alternating normal and superconducting regions.

In order to make the total area of the interface within the superconductor as

large as possible, the size of the regions must be as small as possible. This

was supposed to be the case even for a long cylinder in a longitudinal mag-

netic ﬁeld, in contradiction to experimental evidence existed at that time.

Experiments showed that such a separation of the normal and superconduct-

ing regions took place only for samples with a non-zero demagnetizing factor

(the intermediate state). Moreover, the layers were rather thick (∼1 mm),

which could only be the case if σ

> 0, which also contradicted the London

theory.

This contradiction was reconciled by a theory proposed by Ginzburg and

Landau, which was also phenomenological but took into account quantum

eﬀects [313]. In that moment, it became clear why it is so important to include

1.5 Theories of Superconductivity 27

quantum eﬀects in considerations. Assume that there is a wave function (or

order parameter) Ψ, describing the electrons quantum-mechanically. Then, the

squared amplitude of this function (which is proportional to n

)mustbezero

in a normal region, increase continuously through the normal-superconducting

interface and ﬁnally reach a certain equilibrium value in a superconducting

region. Therefore, a gradient of Ψ must appear at the interface. At the same

time, as is known from quantum mechanics, |∇Ψ |

is proportional to the

density of the kinetic energy. So, quantum eﬀects taken into account lead

to an additional positive energy stored at the interface, which creates the

opportunity to obtain σ

> 0.

Tremendous importance of the Ginzburg–Landau theory consisted in that

it introduced quantum mechanics into the description of superconductors.

It assumes the description of the total number of superconducting electrons

by a wave function, depending on spatial coordinates (or equivalently, a wave

function of n electrons is a function of n coordinates, Ψ(r

, r

,...,r

)). Based

on this, the theory established the coherent (coupled) behavior of all super-

conducting electrons. Indeed, in quantum mechanics, a single electron in the

superconducting state is described by a function Ψ(r). If we now have n

absolutely identical electrons (where n

, the superconducting electron num-

ber density, is a macroscopically large number), and all these electrons behave

coherently, it is obvious that the same wave function of a single parameter

is suﬃcient to describe each of them. This idea permitted to involve in the

description the superconductivity quantum eﬀects, at the same time, retaining

macroscopic featuresofthematerial.

It is interesting that analysis of experimental data on the basis of the

Ginzburg–Landau theory permitted to estimate eﬀective charge, e

∗

,which

rendered approximately two times greater than electron charge. However, then

nobody had any idea about coupling of electrons, while the Ogg’s paper (1946)

that was published some years ago contained the idea about coupling of the

electrons with their further Bose–Einstein condensation.

The Ginzburg–Landau theory was built on the basis of the theory of

second-order phase transitions (the Landau theory) [595] and, therefore, it

is valid only in the vicinity of the critical temperature. By applying the

Ginzburg–Landau theory to superconducting alloys, Abrikosov in 1957 devel-

oped a theory of the so-called type-II superconductors [3]. It turned out that

superconductors need not necessarily have σ

> 0. Materials that provide

this condition are type-I superconductors and transition in external magnetic

ﬁeld from superconducting state to normal one for them is the phase transi-

tion of I type. However, the majority of superconducting alloys and chemical

compounds demonstrate σ

< 0, and they are type-II superconductors. For

type-II superconductors, there is no Meissner eﬀect; magnetic ﬁeld penetrates

inside the material but in a very unusual way, that is, in the form of quantized

vortex lines (quantum eﬀect on the macroscopic scale!). Superconductivity in

these materials can survive up to very high magnetic ﬁelds, and transition in

external magnetic ﬁeld from superconducting state to normal one for them