Панченков Г.М., Лебедев В.П. Химическая кинетика и катализ

Подождите немного. Документ загружается.

Для определения числа активных молекул необходимо найти ве-

роятность сосредоточения m квантов на одном из s осцилляторов

при

условии, что молекула в целом обладает i квантами энергии.

Иными

словами, необходимо найти вероятность такого рас-

пределения, когда энергией е = е

= mhv обладает один осцил-

лятор,

а энергией е — (/— m)hv все остальные s— 1 осцилля-

торов.

Теория

Касселя, по этой логике,

дает

для константы скорости

мономолекулярной реакции выражение:

(20)

Таким

образом, процесс идет с энергией активации

= Nz

= N

Однако этот

результат

справедлив только в том случае, когда

скорость реакции прямо пропорциональна концентрации в первой

степени,

т. е. если реакция протекает при больших давлениях.

При

малых давлениях теория

дает

иное значение энергии ак-

тивации

^ =

-(s-i)RT

(21)

Уменьшение энергии активации с уменьшением давления по-

зволяет понять, почему опытные данные редко согласуются с

даваемой теорией Гиншельвуда линейной зависимостью k~

—

f(p-'V

Уменьшение энергии активации приводит к увеличению

значения

k при уменьшении давления, что не согласуется с зависи-

мостью, даваемой уравнением (9).

В качественном отношении теория Касселя является значитель-

ным

шагом вперед по сравнению с теорией Гиншельвуда. Однако

ней теоретически не определен множитель А в основном уравне-

нии

(20). Как и в теории Гиншельвуда, совпадение результатов

теории и опыта происходит только при подборе числа колебатель-

ных степеней свободы s, что не может не вызвать определенной

неудовлетворенности при обосновании применимости теоретических

соотношений

к эксперименту.

В теории Слетера молекула рассматривается как механическая

система, состоящая из N атомов, каждый из которых совершает

гармонические колебания. Взаимодействие молекул осуществ-

ляется только при столкновении. В промежутки времени

между

столкновениями

каждый атом сохраняет имеющийся у него запас

колебательной энергии, перераспределение которой возможно

только в момент столкновения. Активной молекулой, по Слетеру,

является только та, у которой на одной или нескольких координа-

тах сосредотачивается энергия, равная или большая некоторого

критического значения е

. При этом в молекуле в целом сосредото-

чивается энергия

где суммирование проведено по всем колебательным координатам

молекулы.

Условие (22) является необходимым, по недостаточным. Кроме

этого условия необходимо, чтобы произошло сосредоточение

энер-

гии,

равной или большей е

на определенной связи.

Исходя из этих предположений, Слетер получил формулу для

константы

скорости при высоких давлениях (точнее, для предель-

ной

константы при бесконечно больших давлениях)

k^ = v exp (—

aKt

/RT)

(23)

где

(24)

(v; — частоты нормальных колебаний молекулы). Сравнивая (23)

с (20), можно увидеть, что теория Слетера

дает

истолкование не-

определенного в теории Касселя множителя А и открывает воз-

можность его расчета по экспериментальным данным (частотам

колебаний

атомов в молекуле).

В предельном

случае

малых давлений теория Слетера также

дает

переход к бимолекулярному закону и, подобно теории Кас-

селя,

объясняет эффект уменьшения энергии активации с умень-

шением

давления. Для некоторых реакций рассматриваемая тео-

рия

приводит к удовлетворительному согласию теории с экспери-

ментом.

6. Мономолекулярные реакции в теории

активированного комплекса

Активированный комплекс при мономолекулярном превращении

по

своим свойствам близок к исходной молекуле, однако его коле-

бательные суммы значительно отличаются от ф

ол исходных моле-

кул. В меньшей мере отличаются Q

Bpam

, так как слегка изменяются

межатомные расстояния. Поступательные же суммы состояний

(поскольку массы основного и активного состояний равны)

будут

равны

и сократятся в уравнении для константы скорости. Без су-

щественной ошибки можно полагать, что факторы симметрии б

будут

одинаковыми в основном и переходном состояниях. Под-

ставляя значение статистических сумм в уравнение, определяющее

константу скорости, и сократив равные множители в числителе и

знаменателе, получим основное уравнение теории активированного

комплекса

для мономолекулярных реакций:

h Q

\ — ~dr ) =

х-г

lyl

1 = 1

ехр -

(25)

158

159

где /

, /„, /, и it, if, it —главные моменты инерции молекулы в основном

переходном состояниях: v

n vf — частоты колебания в основном и пере-

ходном состояниях.

Поскольку в активированном комплексе

отсутствует

одна ко-

лебательная степень свободы, один из множителей в колебатель-

ной

сумме состояний, соответствующий частоте колебания вдоль

разрываемой связи, исчезает.

Упростим уравнение (25), положив

(/«/

/z)

** (/* 1ц I* У .

рассмотрим два предельных случая. Первый случай, когда Av, <C

«С kT и hvf < kT,

тогда,

поскольку [1 — ехр (—hv/kT)] ж

ж hv/kT, получаем

t-зл-и

П v,

А-Х

кТ

-E*!RT

(26)

д i = 3N-7

»?

(-1

Частоты в активной молекуле вряд ли сильно отличаются от

частот в основном состоянии и

могут

быть сокращены. Поэтому

в числителе уравнения (26) останется одна частота колебания раз-

рываемой связи

k^xve-

Eu!RT

(27)

Это уравнение формально аналогично уравнению (23), полу-

чающемуся в теории Слетера, и при предположении, что А=\,

уравнению (20) в теории Касселя. Поскольку v имеет порядок.

—10

с~

это уравнение согласуется с экспериментальными

данными для большого числа реакций.

Второй случай, когда /iv, >A7" и

ftvi*

^$>

kT, Тогда, поскольку

—ехр

(—hv/kT)] » 1, получаем

T ~р

—г- е

(28)

Для температур от 300 до 1000 К, при которых обычно проводят

реакции,

множитель kT/h соответственно равняется

6,6-10

с~

2,1-10

с~

т.е. имеет порядок 10

—10

(Н, что также согла-

суется с опытом.

Таким образом, теория активированного комплекса для боль-

шинства реакций, как это видно из данных табл. 14, удовлетвори-

тельно объясняет опытное значение предэкспоненциального мно-

жителя. Однако наблюдаются и отклонения, не укладывающиеся

в рамки рассуждений, следствием которых являются уравнения

(27) и (28). Например, для распада N

O и

предэкспонен-

циальный множитель имеет порядок I0

, для распада

NCH

равен 2,1

•

, для распада

NC,H

2,8-10

для распада Sn(CH

)4 —

даже

8-Ю

Подобные отклонения не

могут

быть объяснены приближениями, сделанными при выводе

уравнений (27) и (28). Можно предположить, что в данном слу-

чае вероятность образования активированного комплекса значи-

тельно отклоняется от единицы. Это легко учесть, если воспользо-

160

ваться основным уравнением теории активированного комплекса

в термодинамическом виде:

Считая х— 1» из (29) получаем уравнение для расчета значе-

ния

энтропии активации, если известны опытные константа ско-

рости и энергия активации

(30)

Если энтропия активации положительная, т. е. активирован-

ный

комплекс представляет собой менее упорядоченную

структуру

по

сравнению с основным состоянием, предэкспоненциальный мно-

житель

будет

больше kT/h [распад

NCH

=NC

Si(CH

)

Sn(CH

)

Наоборот, в

случаях,

когда об-

разование активированного комплекса связано с упорядочением

структуры, т. е. энтропия активации является отрицательной вели-

чиной,

опытное значение предэкспоненциального множителя

будет

аномально низким (распад N

В табл. 14 приведены

значения

AS, вычисленные по уравнению (30). Как видно, в боль-

шинстве случаев энтропия активации невелика, следовательно,

предположение о подобии активированного комплекса исходной

молекуле часто является допустимым. Однако надо помнить, что

это допущение справедливо лишь для мономолекулярных реакций.

В общем случае, как отмечалось выше, незнание конфигурации

свойств активированного состояния в подавляющем большинстве

случаев не

дает

возможности провести количественное сопоставле-

ние

теории с экспериментом.

Лучше

согласуется с опытом теория Маркуса, в основу которой

положена теория Раиса, Рамспергера, Касселя, получившая назва-

ние

РРКМ

по начальным буквам фамилий авторов. В этой теории

константа скорости активации рассчитывается квантовомеханиче-

ски,

а константа скорости дезактивации — из числа дезактивирую-

щих столкновений. Возникшие активные молекулы вследствие

столкновений с любыми частицами М превращаются в молекулы

активирующего комплекса и только потом в конечные продукты.

Ввиду

громоздкости и сложности вычислений, отсылаем читате-

лей к книге Н. Робинсона и К. Холбрука (см. список литературы).

7. Тримолекулярные реакции в газовой фазе

Известны четыре реакции в газовой фазе с участием моноксида

азота, кинетически являющиеся процессами третьего порядка!

2NO

+ Oj —*

2NO

2NO+CU

—• 2NOC1

—»- 2NOBr

—*

O+N

(или

2NO + 2Hj —*• N

+ 2H

6 S.K. W0 16!

Кроме

этих процессов, тримолекулярными являются реакций ре-

комбинации

валентно-ненасыщенных частиц:

M +

R'+R*

—> R'R*+M

где М —

любая

частица;

R —

атом

со

свободной

валентностью

или

радикал.

Для тримолекулярной рекомбинации характерно, что третья

частица не принимает непосредственно участия в химическом про-

цессе, стехиометрически являющемся бимолекулярным:

R' + R" —• R'R*

а лишь способствует стабилизации, отводя избыточную энергию

от молекулы R'R". Таковы, например, следующие процессы:

+ Н + М —*. Н

+ М

(М-Н

)

Вг

+ М —*•

Вг

+ М (М - Вг

)

ОН

+ ОН + М —•

-f

М (М -

, О

О)

+ ОН + М —• Н

О + М (М -

О)

Как

уже указывалось, эффективность стабилизирующего трой-

ного столкновения тем больше, чем больше атомов в молекуле

третьей частицы М. Дело в том, что увеличение числа колебатель-

ных степеней свободы увеличивает вероятность отвода энергии от

вновь образованной молекулы на межатомные связи молекулы М.

Это подтверждается приведенными ниже опытными данными при

рекомбинации

атомного иода (при

25°С)

I + I-J-M = l2 + M в

присутствии различных стабилизирующих добавок:

М Не Ne Аг Кг Хе Н,

А,

см

/{моль

•

с)

по

данным

Хрнстн,

Норриша

Портера

1,73 1,86 2,42 3,41 3,44 —

Рассела

Саймонса

0,94 1,00 2,00 — — 2,63

М О

СОа СС1

СН

ОН С

С1 СцН

СН

к,

см

/(моль

•

с)

по

данным

Рассела

Саймонса

.... 3,69 7,44 28,0 35,8 46,3 183

Как

видно, для атомных стабилизаторов (инертные газы) эф-

фективность стабилизации растет с увеличением атомной массы,

для молекулярных — с ростом числа атомов в молекуле. Правда,

при

более детальном рассмотрении наблюдается и некоторая спе-

цифичность

действия, например, А

Са

а ™ 46,3, £с

вг=14, 2

£с

=я

38> но общая картина остается типичной.

Наиболее характерным для тримолекулярных реакций яв-

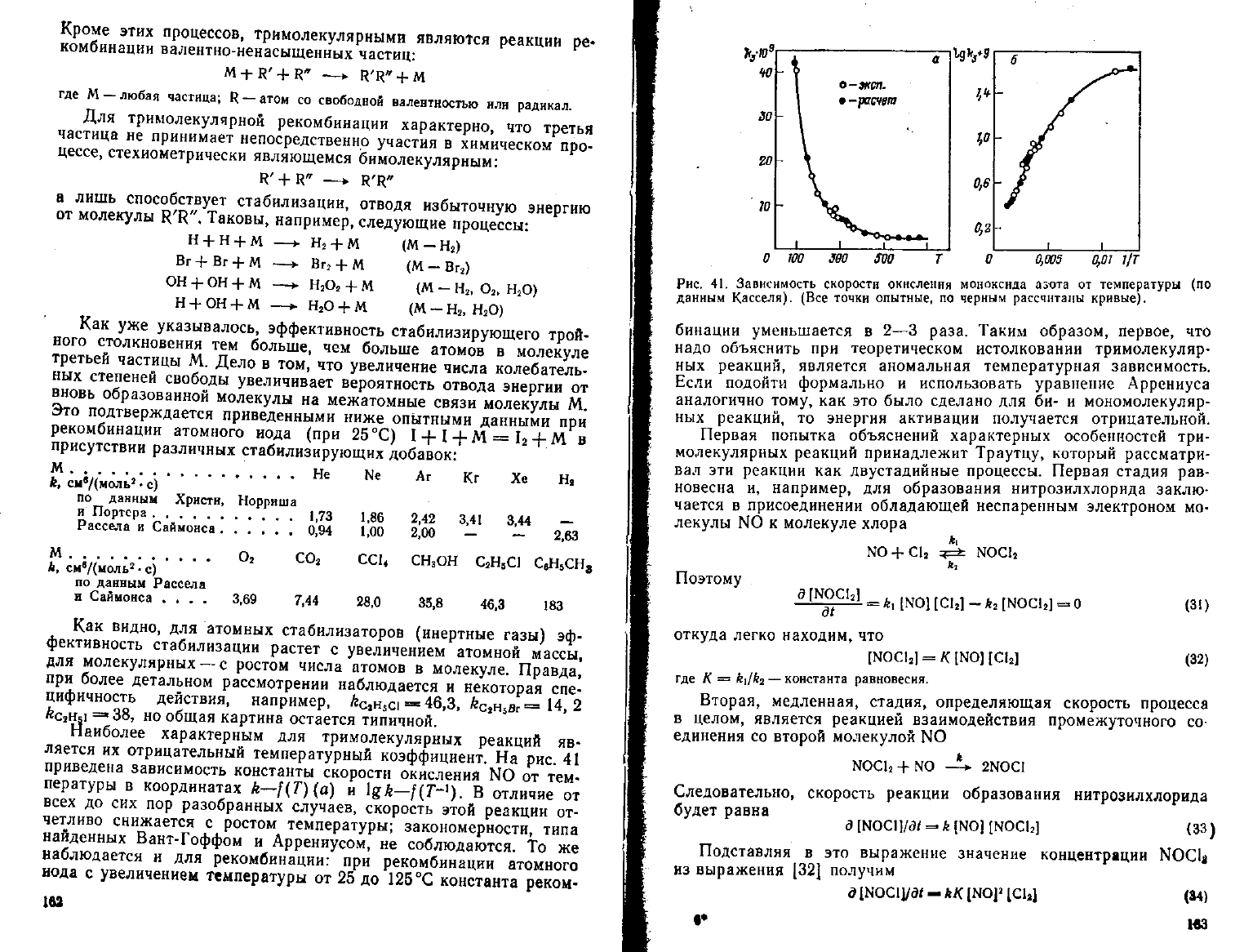
ляется их отрицательный температурный коэффициент. На рис. 41

приведена зависимость константы скорости окисления NO от тем*

пературы в координатах k—f(T)(a) и \gk—f(T-~

). В отличие от

всех

до сих пор разобранных случаев, скорость этой реакции от-

четливо снижается с ростом температуры; закономерности, типа

найденных Вант-Гоффом и Аррениусом, не соблюдаются. То же

наблюдается и для рекомбинации: при рекомбинации атомного

иода с увеличением температуры от 25 до 126 °С константа реком-

163

V»'

0,005

0,01 l/T

Рис. 41.

Зависимость

скорости

окисления

моноксида

аз^та

от

температуры

(по

данным

Касселя). (Все

точки

опытные,

по

черным

рассчитаны

кривые).

бинации

уменьшается в 2—3 раза. Таким образом, первое, что

надо объяснить при теоретическом истолковании тримолекуляр-

ных реакций, является аномальная температурная зависимость.

Если

подойти формально и использовать уравнение Аррениуса

аналогично

тому,

как это было сделано для би- и мономолекуляр-

ных реакций, то энергия активации получается отрицательной.

Первая

попытка объяснений характерных особенностей три-

молекулярных реакций принадлежит

Траутцу,

который рассматри-

вал эти реакции как двустадийные процессы. Первая стадия рав-

новесна

и, например, для образования нитрозилхлорида заклю-

чается в присоединении обладающей неспаренным электроном мо-

лекулы NO к молекуле хлора

Поэтому

NOCl

ft, [NO] [Cl

] - *

[NOC1

]

=> 0

(31)

откуда легко находим, что

[NOC1

]

= /С [NO] IC1

] (32)

где К =

k]fk

—

константа

равновесия.

Вторая, медленная, стадия, определяющая скорость процесса

целом, является реакцией взаимодействия промежуточного со-

единения

со второй молекулой N0

NOCb + NO

2N0CI

Следовательно, скорость реакции образования нитрозилхлорида

будет

равна

[NOCll/df

=•

* (NOJ [NOCh] (33)

Подставляя в это выражение значение концентрации NOCla

из

выражения [32] получим

[HOCiydt

- кК [NOP

[Clal

(U)

•• 163

т. е. процесс является реакцией третьего порядка. По Траутцу,

ростом температуры равновесие сдвигается в сторону диссоциа-

ции

промежуточного соединения типа

NOC1

Таким образом, со-

гласно уравнению (33), скорость снижается с повышением темпе-

ратуры за счет уменьшения концентрации

NOC1

Наблюдаемая

на

опыте константа скорости есть произведение истинной бимоле-

кулярной

константы скорости на константу равновесия, уменьше-

ние

которой с ростом температуры и приводит, согласно уравне-

нию

(34), к наблюдаемой аномальной температурной зависимости

АотТи

IgAoT

T-K

Рассмотрим,

как

могут

быть объяснены тримолекулярные реак-

ции

по теории столкновений.

Число

тройных соударений может быть найдено при условии,

что известна длительность двойного соударения. Если считать мо-

лекулы идеально упругими шарами, то двойное столкновение мгно-

венно

и участие в нем третьей частицы невозможно. Задача рас-

чета числа тройных столкновений решается, если отказаться от

представления о тройном столкновении как о моменте нахожде-

ния

центра третьей молекулы на поверхности сферы, радиус кото-

рой

равен сумме радиусов

двух

столкнувшихся молекул. Необхо-

димо рассматривать конечную длительность пребывания центра

малой молекулы в шаровом слое с радиусом, равным СТАВ и СТАВ +

б (СТАВ = ГА -f- гв — сумма радиусов сталкивающихся молекул А

В). При этом б — величина неопределенная, что ограничивает

возможность количественных расчетов.

Число

тройных столкновений

между

молекулами

трех

различ-

ных видов в одном кубическом сантиметре в секунду равно

(35)

где

ЦАВ

ЦВС

— приведенные массы молекул АВ и ВС.

Сравнивая

выражение для тройных соударений (35) с выраже-

нием

для числа двойных соударений:

(36)

нетрудно

увидеть,

что г\ц отличается от z\

Если принять, что

тп\

= гпъ = тс и

СТАВ

= о

ас

— стде, то, сопо-

ставляя выражение (35) с (36), найдем при условии л

=«

Так

как <т да 10~

см и б, по-видимому, того же порядка,

г\тз/г%

Для идеального газа число молекул в одном кубическом сан-

тиметре равно п =zp/kT. Следовательно, число тройных столкнове-

ний

пропорционально

кубу,

а двойных — квадрату давления.

При

малых и средних давлениях число двойных столкновений зна-

• Выполнение этого условия фиксируется верхним индексом

снуль»

у ве-

личины г.

164

льно превышает число тройных, однако с повышением давле-

это

соотношение изменяется в пользу тройных столкновений.

т относительного роста числа тройных столкновений важен

.истолкования

многих химических процессов, идущих с по-

№ю

тройных столкновений, в том числе для объяснения пре-

сных явлений при взрывах (см. гл. VII, § 6).

Константа

скорости тримолекулярной реакции может быть лег-

' найдена умножением величины

г°|

на

аррениусовский

экспо-

щиальный

множитель:

(38)

(нако

результаты расчета по этому уравнению не согласуются

ЙШТНЫМИ.

Из

выражения (38) вытекает, что если величина zJ

постоянна,

, константа скорости должна увеличиваться с ростом темпера-

№Ы.

Но выше было сказано, что константа скорости тримолеку-

1рных реакций уменьшается с ростом температуры. Кроме того,

величину г}

входит неопределенный множитель б, что сильно

крудняет расчеты.

Множитель б для неидеальных систем должен зависеть от тем-

вратуры, так как с изменением температуры меняется кинетиче-

сая

энергия сталкивающихся частиц, а следовательно, и энергия

взаимодействия. Изменение энергии взаимодействия может

гь учтено поправкой Сезерленда, т. е. можно положить, что

- 1 + (Фо/ЯГ) (39)

Фо

— постоянная, связанная с энергией взаимодействия.

Тогда

Поэтому

для неидеальных систем

(41)

Из

выражения (41) после логарифмирования и дифференциро-

вания

по Г получаем

d In k Фо , Е

TiRT

/г

(42)

. го уравнение

дает

кривую зависимости k от Т-\ качественно сов-

падающую с кривой рис. 41,6. Однако неопределенность величины

•<ро

делает количественные выводы весьма ненадежными. В связи

_ этим многие исследователи ограничиваются эмпирическими за-

Пвисимостями

константы скорости от температуры. Например, для

"реакции

2NO -f СЬ эмпирическая зависимость константы скорости

;от температуры имеет вид

!g ft =

490/Г

+ 10,5 lg 7* —

20.697

а для реакции 2NO -f H

lg к — 38 682

•

2/Г -

66,37

lg T +

245,410

165

8. Тримолекулярные реакции в теории

активированного комплекса

Основной трудностью применения теории активированного ком-

плекса к тримолекулярным реакциям является отсутствие сведе-

ний

о составе и

структура

переходного состояния. Обычно прини-

мают, что активированный комплекс состоит из

трех

молекул, при-

нимающих участие в реакции согласно стехиометрическому

уравнению. Структура активированного комплекса значительно

более упорядочена по сравнению с исходным состоянием, и энтро-

пия

активации должна быть существенно более отрицательной

(AS^-'CO). Качественно это обстоятельство согласуется с малым

значением стерического множителя, полученным при истолковании

тримолекулярных реакций по теории столкновений. Для реакции

с участием N0 активированный комплекс, согласно сделанному

предположению, имеет состав (N0)2X2, где Хг — О

, С1г, Вг

, Нг.

Его

структура

остается неопределённой. Для конкретного расчета

константы скорости в

случае

взаимодействия N0 с 0

и СЬ Эйринг

Гершинович выбрали прямоугольную

структуру

активирован-

ного комплекса:

-О О" О--О

*N—N*

N N

II II У

0 0 0 0

Молекула

Активированный

комплекс

Основанием для такого выбора является направление валентностей

в молекулах кислорода и моноксида азота.

Таким образом, шестиатомный активированный комплекс обла-

дает

четырьмя поступательными степенями свободы, одна из кото-

рых уже учтена в основном уравнении теории активированного

комплекса, тремя вращательными и 3-6 — 7=11 колебатель-

ными.

Отсюда для реакции

2N0

+ Xj *=*

ONXXNO

—•

2N0X

Поступательная

составляющая

статистическая сумма состояния активированного комплекса равна

(43)

а*А

Вращательная

составляющая

-1

Колебательная

составляющая

Общее выражение для константы скорости в предположении,

что трансмиссионный коэффициент %= 1 в все исходные молекулы

двухатомны,

будет

иметь вид

-E/RT,

a**'

-1

-EtfRT

(44)

где о+ и oi — факторы симметрии; g+ и £* —электронная мультнплетность

активированного комплекса и исходного состояния соответственно.

Разделим все члены выражения [44] на зависящие и не зави-

сящие от температуры: последние обозначим через G. Тогда

3 \2nkJ

V'-,.*•'•

(/+/•/•)*

(4S)

«к

1-1

(46)

i-l

Прологарифмировав [46] получим

k — In

- у In Г -f In Д [1 - exp (- Avj/АГ)] -

i-i

Гп

Д [l - exp (- hvf/kT)] -

E/RT

(47)

i-1

160

Остановимся прежде всего

на

некоторых соображениях каче-

ственного характера, возникающих

связи

приведенными

вы-

кладками. Уравнения

[44] и [46]

показывают,

что

скорость

три-

молекулярной реакции действительно должна весьма заметно

уменьшаться

ростом температуры (константа скорости обратно

пропорциональна

Г'

) при

условии,

что

энергия активации имеет

конечную величину

и в

соответствии

с ее

физическим смыслом

положительна. Таким образом, теория активированного комплекса

дает

качественное объяснение экспериментальной температурной

зависимости тримолекулярной реакции.

оказывается

воз-

ножным

по

опытным данным провести расчет истинной энергии

167

активации

три молекулярного процесса. Для этого достаточно по-

строить график зависимости

in k + - In T + in

i-l

•'(+)

(48)

по тангенсу

угла

наклона получающейся прямой определить

энергию активации. Возможность количественной проверки теории

серьезно осложняется отсутствием данных о частотах колебания

активированного комплекса. Приближенные пути проверки рас-

смотрим на примере реакции окисления N0. Гипотетическая струк-

тура

активированного комплекса такая, как было показано выше.

В связи с принятой геометрической моделью одна колебательная

степень свободы заменяется на вращательную по связи О—О, по-

этому остается 10 колебательных степеней свободы, и в [49] по-

является множитель

(8л

1ооЬТ/Н

)Ч*

(где /оо — момент инерции

вокруг оси связи О—О). Исходя из этого, получаем для константы

скорости следующее выражение:

k =

кТ

а*Л

(2nm

kTf

.-E.IRT.

п["--(-#)]

-1

—(-»]•[—

-2

-B/JW

где

учитывая,

что

оо

2 и а«о •• 1

О-х

Ч2яА/

(М)

>>"*NO'Oj'

1ва

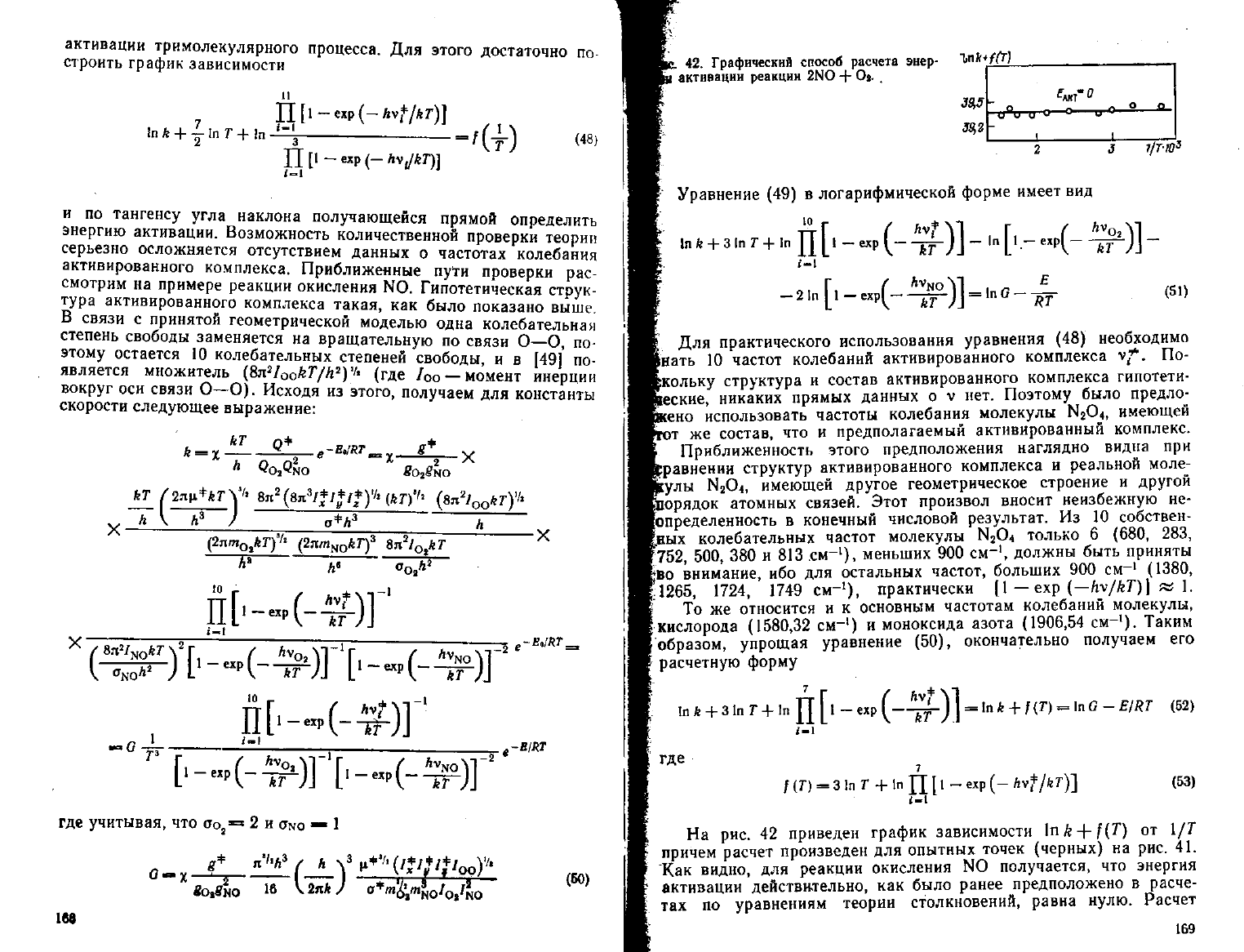
. 42.

Графический

способ

расчета

энер-

актнвацнн реакции 2NO -f- Oj.

39,5

39,2

7/Т-Ю

Уравнение (49) в логарифмической форме имеет вид

+ 3

1п

Д [t -

ехр

(

~^J

J -

[l -

ехр(-

i-l

(5,)

Для практического использования уравнения (48) необходимо

^ 10 частот колебаний активированного комплекса vf. По-

скольку

структура

и состав активированного комплекса гипотети-

ческие,

никаких прямых данных о v нет. Поэтому было предло-

жено использовать частоты колебания молекулы

имеющей

эт же состав, что и предполагаемый активированный комплекс.

Приближенность

этого предположения наглядно видна при

Сравнении

структур

активированного комплекса и реальной моле-

£улы

имеющей

другое

геометрическое строение и

другой

порядок

атомных связей. Этот произвол вносит неизбежную не-

определенность в конечный числовой

результат.

Из 10 собствен-

ных колебательных частот молекулы

только 6 (680, 283,

Г752,

500, 380 и 813 см-

), меньших 900 см-

, должны быть приняты

•JBO внимание, ибо для остальных частот, больших 900 см

-1

(1380,

1265, 1724, 1749 см-

), практически (1

—ехр

(—hv/kT)) « 1.

То же относится и к основным частотам колебаний молекулы,

;кислорода

(1580,32

см~

) и моноксида азота

(1906,54

см-

). Таким

образом, упрощая уравнение (50), окончательно получаем его

расчетную форму

lnfe

T + In

exp

In ft + / (T) = In G - EIRT (52)

где

/ (Г) = 3 In Г + In П [

- ехр (-

Avf/ftГ)]

(53)

(-1

На

рис. 42 приведен график зависимости \nk-\-f{T) от 1/7"

причем расчет произведен для опытных точек (черных) на рис. 41.

Как

видно, для реакции окисления NO получается, что энергия

активации

действил-ельно, как было ранее предположено в расче-

тах по уравнениям теории столкновений, равна нулю. Расчет

169

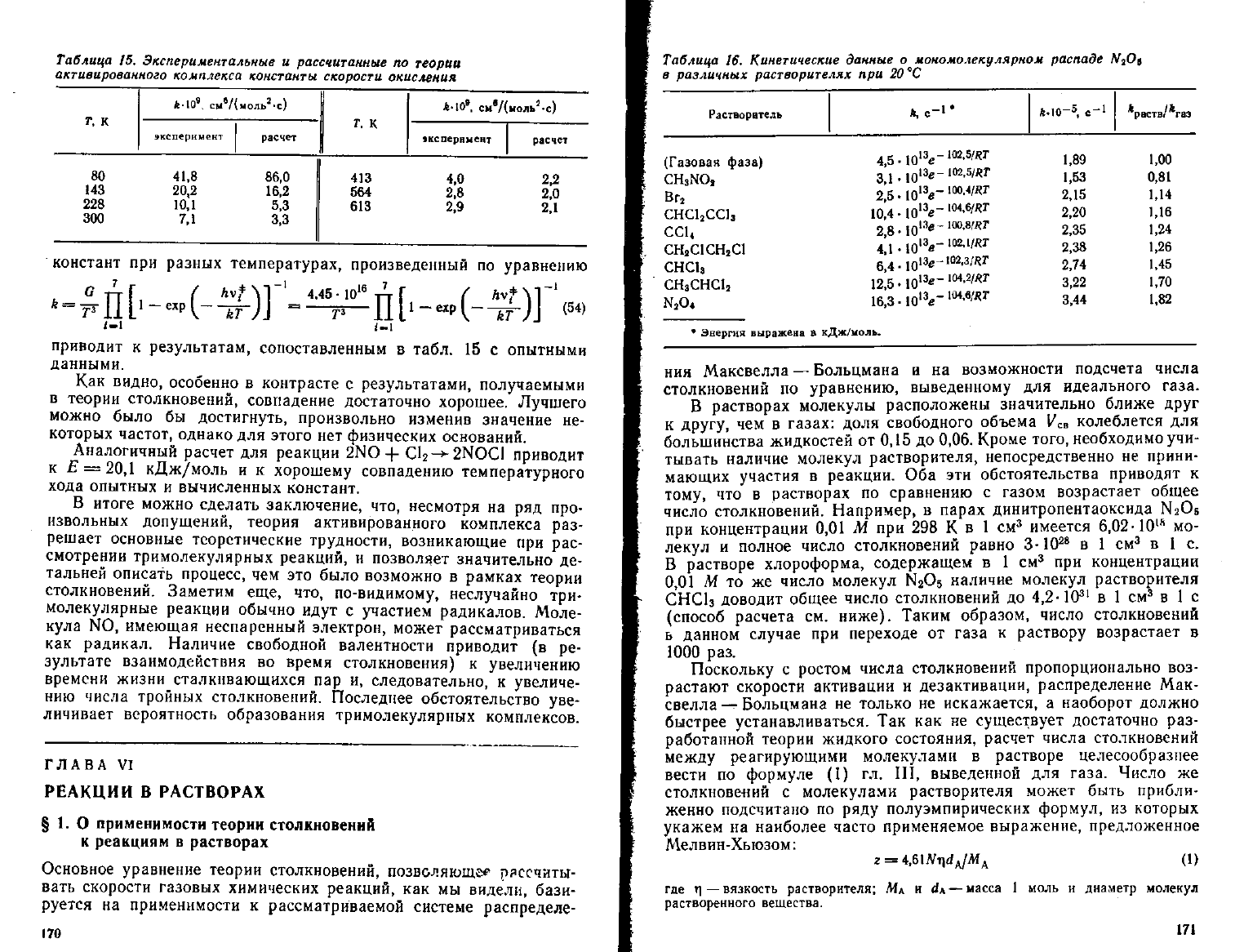
Таблица 15.

Экспериментальные

рассчитанные

по

теории

активированного

комплекса

константы

скорости

окисления

Т. К

МО

си

/{моль

-с)

эксперимент

расчет

80 41,8 86,0

143 20,2 16,2

228 10,1 5,3

300 7,1 3.3

Г.

МО» cn

/UoJib

.c)

жспериыент расчет

413 4,0 2,2

564 2,8 2,0

613 2,9 2,1

констант

при разных температурах, произведенный по уравнению

RV{)\

(54)

4.45 - 10

приводит к результатам, сопоставленным в табл. 15 с опытными

данными.

Как

видно, особенно в контрасте с результатами, получаемыми

теории столкновений, совпадение достаточно хорошее.

Лучшего

можно было бы достигнуть, произвольно изменив значение не-

которых частот, однако для этого нет физических оснований.

Аналогичный расчет для реакции 2NO+ С1г-*-2ЫОС1 приводит

£ = 20,1 кДж/моль и к хорошему совпадению температурного

хода

опытных и вычисленных констант.

В итоге можно сделать заключение, что, несмотря на ряд про-

извольных допущений, теория активированного комплекса раз-

решает основные теоретические трудности, возникающие при рас-

смотрении тримолекулярных реакций, и позволяет значительно де-

тальней описать процесс, чем это было возможно в рамках теории

столкновений.

Заметим еще, что, по-видимому, неслучайно три-

молекулярные реакции обычно

идут

с участием радикалов. Моле-

кула NO, имеющая неспаренный электрон, может рассматриваться

как

радикал. Наличие свободной валентности приводит (в ре-

зультате

взаимодействия во время столкновения) к увеличению

времени жизни сталкивающихся пар и, следовательно, к увеличе-

нию

числа тройных столкновений. Последнее обстоятельство уве-

личивает вероятность образования тримолекулярных комплексов.

ГЛАВА

РЕАКЦИИ

В РАСТВОРАХ

§1.0 применимости теории столкновений

реакциям в растворах

Основное уравнение теории столкновений, позволяющее ряссчиты-

вать скорости газовых химических реакций, как мы видели, бази-

руется на применимости к рассматриваемой системе распределе-

но

Таблица 16.

Кинетические

данные

мономолекулярном

распаде

различных

растворителях

при 20"С

Растворитель

ft.10

с"

в/

*раств/

газ

(Газовая фаза) 4,

NO»

Вг

CHCl

CCh

10,

СС1

СН

С1СН

С1

СНСЬ

СНзСНСЬ

12,

NjO

16,

Энергия выражена

кДж/моль.

1,89

1,53

2,15

2,20

2,35

2,38

2,74

3,22

3,44

1,00

0,81

1,14

1,16

1,24

1,26

1,45

1,70

1,82

ния

Максвелла — Больцмана и на возможности подсчета числа

столкновений

по уравнению, выведенному для идеального газа.

В растворах молекулы расположены значительно ближе

друг

другу,

чем в

газах:

доля свободного объема V

колеблется для

большинства жидкостей от 0,15 до 0,06. Кроме того, необходимо учи-

тывать наличие молекул растворителя, непосредственно не прини-

мающих участия в реакции. Оба эти обстоятельства приводят к

тому,

что в растворах по сравнению с газом возрастает общее

число столкновений. Например, в парах динитропентаоксида

при

концентрации 0,01 М при 298 К в 1 см

имеется 6,02- Ю

1Й

мо-

лекул и полное число столкновений равно

3-Ю

в 1 см

в I с.

В растворе хлороформа, содержащем в 1 см

при концентрации

0,01 М то же число молекул N2O5 наличие молекул растворителя

СНСЬ

доводит общее число столкновений до

4,2-10

в 1 см

в 1 с

(способ расчета см. ниже). Таким образом, число столкновений

данном

случае

при переходе от газа к раствору возрастает в

1000 раз.

Поскольку

с ростом числа столкновений пропорционально воз-

растают скорости активации и дезактивации, распределение Мак-

свелла—Больцмана не только не искажается, а наоборот должно

быстрее устанавливаться. Так как не

существует

достаточно раз-

работанной теории жидкого состояния, расчет числа столкновений

между

реагирующими молекулами в растворе целесообразнее

вести по формуле (1) гл. III, выведенной для газа. Число же

столкновений

с молекулами растворителя может быть прибли-

женно

подсчитано по ряду полуэмпирических формул, из которых

укажем на наиболее часто применяемое выражение, предложенное

Мелвин-Хыозом:

(1)

где л — вязкость растворителя; Мк и </д — масса 1 моль и диаметр молекул

растворенного вещества.

171

Рис.

43. Зависимость

Igft

от 1/7" для ре-

акции разложения C2H4F2 (по данным Мел-

внн-Хьюза).

Для формального описания ско-

ростей протекания химических ре-

акций

в растворах можно приме-

нять

основной постулат химической

кинетики.

Сравнение'

скоростей протекания химических реакций в рас-

творе и в газовой фазе показывает, что в ряде случаев они мало

различаются. В табл. 16 приведены данные о скорости разложения

пентаоксида азота (V) в газовой фазе и различных растворителях.

Как

видно из табл. 16, изменения энергии активации практи-

чески целиком лежат в рамках допустимых опытных ошибок и

можно констатировать постоянство

кт

при переходе от раство-

рителя к растворителю. Предэкспоненциальный множитель изме-

няется

не более чем в 2 раза. Таким образом, в данном примере

влияние

растворителя крайне незначительно.

Не

только для мономолекулярных, но и для некоторых бимоле-

кулярных реакций в растворах значения констант скоростей и

энергий

активации близки к найденным для реакций в газовой

фазе.

На рис. 43 приведены в координатах \gk— 1/Г данные для

реакции

C2H4I2 —> CjHj + la

газовой фазе и в растворе тетрахлорида

углерода.

Как видно,

обе группы точек практически лежат на одной прямой.

Однако,

как ниже

будет

показано, есть процессы, влияние рас-

творителей на которые весьма существенно.

Скорости

химических

реакций

растворах

По скоростям протекания химические реакции в растворах можно

разделить на определенные группы.

1. Очень быстрые реакции, в которых

отсутствуют

из-

менения

ковалентных связей. В этих реакциях определяющим

является электростатическое взаимодействие ионов. Скорость про-

текания

такого типа реакций зависит главным образом от под-

вода реагирующих веществ

друг

другу

— перемешивания, кон-

векции,

диффузии. Примером

могут

служить реакции:

Ag*

+ cr —> AgCl

Н*

+ ОН~ —* HjO

Н3О4-ОН" —• 2Н

+SOj~ —• BaSO,

очень быстрым реакциям можно отнести также реакции пе-

редачи протона аниону или нейтральной молекуле. Константы ско-

ростей таких реакций, определенные релаксационным методом,

приведены в табл. 17.

'Таблица

17.

Константы

скоростей

реакции

передачи

протона

1с

участием

НаО* при 25 "С

Реакцая

•

2Н

. H

O + H

0 + HF

О* + HOCOO"

+ СН.СОСГ

НзО

+ имидазол

O +

COg

• Н

О + СН

СООН

O+(CH

)

О + катион нмидазолиния

лЛыоль-с

1.4-

7,5-

4,7-

4,5-

2,5-

10"

10'

•

10'°

10'

•

Таблица

18.

Константы

скоростей

реакции

передачи

протона

участием

ОН' при 25 "С

реакция

к, л/(ноль-с|

ОНЧ-NH;

—• H

O + NH

OH4-CH3NHJ —»- H

O +

ОН"

+ HOOCCH

* —> Н

О + HOOCCH

OH~

-f катион имидаэолшшя —*• Н

О + имидазол

OH'

+ HOCOO" •

СО?'

3,3

•

1(Г

3,7 -10

1,1 • 10

2,1-Ю

7-10

Константы

скоростей реакций передачи протона с участием

гидроксила приведены в табл. 18.

2. Быстрые реакции, характеризующиеся высоким зна-

чением стерического множителя (см. гл. III, § 4). Они протекают

между

сложными ионами, в которых происходят изменения кова-

лентных связей, а также

между

некоторыми молекулами.

В табл. 19 приведены значения стерических множителей для реак-

ций

такого типа.

3. «Нормальные> реакции со стерическим множителем,

превосходящим единицу, не более чем в 10

раз.

Таблица

19.

Значения

стерических

множителей

для

некоторых

быстрых

реакций

Реакция

СтернческнЙ

ИИОЖИТ*ЛЬ

[Сг(Н

О)

]

+ CNS

[Co(NH

)

Br]

+ O

1,09-Ю"

1,39-10

38,3

172

173

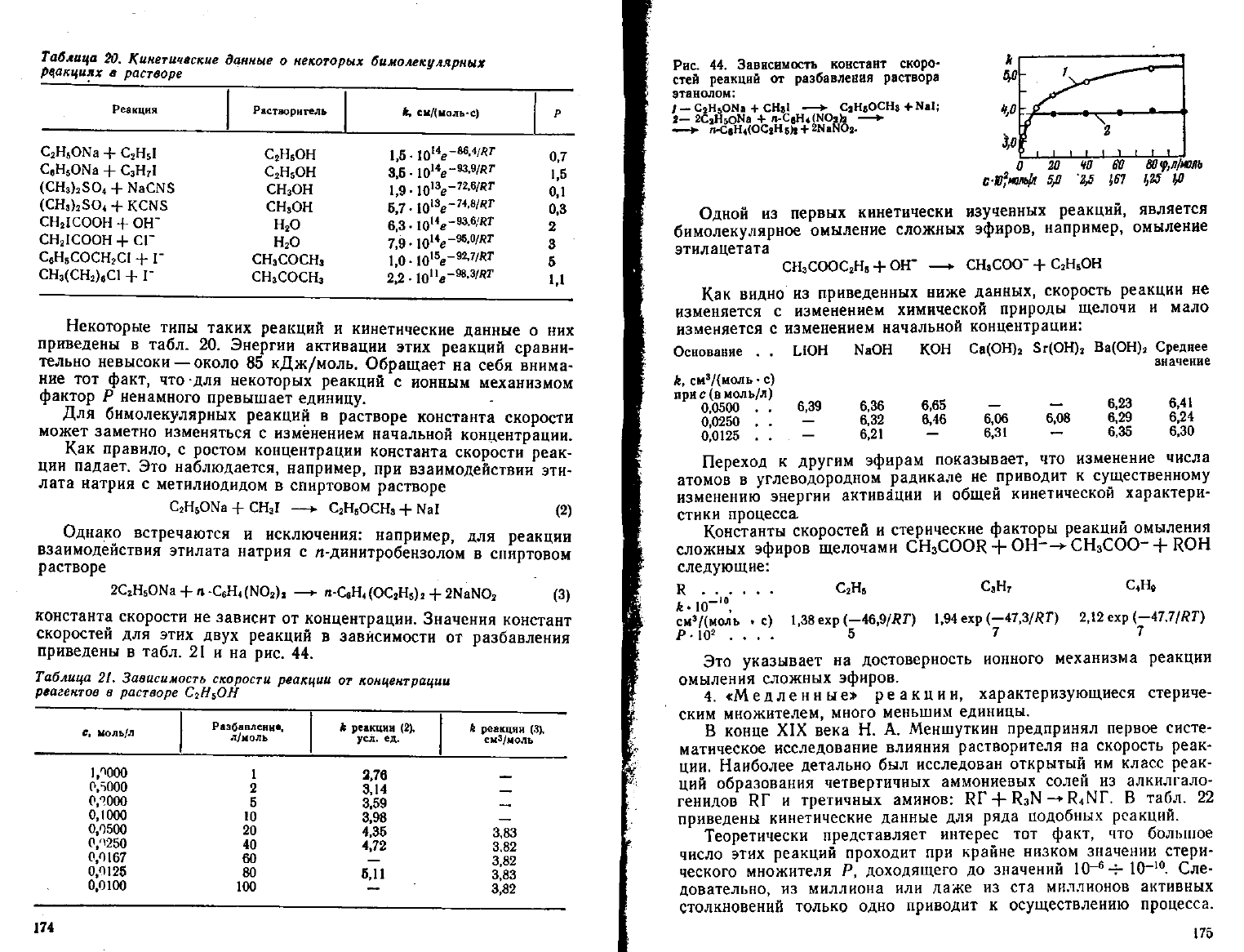
Таблица

20.

Кинетические

данные

некоторых бимолекулярных

реакциях

растворе

Реакция

ONa

Нт1

(CH

)

NaCNS

(CHsbSO^

KCNS

ICOOH-f

0H~

СН

1С00Н

+ СГ

COCH

+ Г

(CH

)

+ Г

Растворитель

ОН

СНзОН

СНаСОСНз

СНзСОСНз

к,

сы/(моль-с)

1,5-Ю

з,б-

IO'V

1,9.10

Б,7-Ю

е-

6,3.10

<Г

7,9-ю

1,0-ю

2,2-Ю

0,7

П,1

1,1

Некоторые типы таких реакций и кинетические данные о них

приведены в табл. 20. Энергии активации этих реакций сравни-

тельно невысоки — около 85 кДж/моль. Обращает на себя внима-

ние

тот факт, что для некоторых реакций с ионным механизмом

фактор Р ненамного превышает единицу.

Для бимолекулярных реакций в растворе константа скорости

может заметно изменяться с изменением начальной концентрации.

Как

правило, с ростом концентрации константа скорости реак-

ции

падает. Это наблюдается, например, при взаимодействии эти-

лата

натрия с метилиодидом в спиртовом растворе

ONa+CH

—*

OCH

+NaI

(2)

Однако встречаются и исключения: например, для реакции

взаимодействия этилата натрия с я-динитробензолом в спиртовом

растворе

2QH

ONa

n-C

(NO

—*•

n-CeH

(OC

)

2NaNO

(3)

константа скорости не зависит от концентрации. Значения констант

скоростей для этих

двух

реакций в зависимости от разбавления

приведены в табл. 21 и на рис. 44.

Таблица

21.

Зависимость скорости реакции от концентрации

реагентов

растворе

ОН

е.

моль/л

Раэбавленн».

л/моль

k реакции

(2),

усл.

ед.

k реакции

(3),

смЗ/моль

1/Ю00

O.iOOO

Р/Ю00

0,1000

0,0500

0/1250

0,0167

0,0125

0,0100

100

2,76

3,14

3,59

3,98

4,35

4,72

—

5,11

—

—.

3,83

3,82

3,83

3,82

174

Рис.

44.

Зависимость констант скоро-

стей реакций

от

разбавления раствора

этанолом:

—CjH

ONa

СН

»-

CjH

OCHs+NaI;

2— 2C

ONa

п-С

Нч(Ж>

)а

H(OCH

2NNO

С-Ю?>юф

Одной из первых кинетически изученных реакций, является

бимолекулярное омыление сложных эфиров, например, омыление

этилацетата

COOC

ОН"

—*-

СНзСОО"

ОН

Как

видно из приведенных ниже данных, скорость реакции не

изменяется с изменением химической природы щелочи и мало

изменяется с изменением начальной концентрации:

Основание

. .

k, см'Дмоль

•

с)

при

(в моль/л)

0,0500

. .

0,0250

. .

0,0125

. .

LiOH

NaOH

КОН Са(ОН)

Sr(OH)

Ba(OH)

Среднее

значение

6,39

6,36

6,32

6,21

6,65

6,46

6,06

6,31

6,08

6,23

6,41

6,29

6,24

6,35

6,30

Переход к

другим

эфирам показывает, что изменение числа

атомов в углеводородном радикале не приводит к существенному

изменению энергии активации и общей кинетической характери-

стики процесса.

Константы скоростей и стерические факторы реакций омыления

сложных эфиров щелочами СН

СОО^ + ОН--»-СНзСОО- + ROH

следующие:

CH СД^

ью-

см

/(моль

.с)

1,38е

р(-46,9/Д7-)

1,94ехр

(-47,3/#Г)

Р.1О

. . . . 5 7

2,12ехр(-47,7//?Г)

Это указывает

на

достоверность ионного механизма реакции

омыления

сложных эфиров.

4. «Медленные» реакции, характеризующиеся стериче-

ским

множителем, много меньшим единицы.

В конце

XIX

века

Н. А.

Меншуткин предпринял первое систе-

матическое исследование влияния растворителя

на

скорость реак-

ции.

Наиболее детально

был

исследован открытый

им

класс реак-

ций

образования четвертичных аммониевых солей

из

алкилгало-

генидов

RF и

третичных аминов:

N—^R^NF.

табл.

приведены кинетические данные

для

ряда подобных реакций.

Теоретически представляет интерес

тот

факт,

что

большое

число этих реакций проходит

при

крайне низком значении стери-

ческого множителя

Р,

доходящего

до

значений

КН ~-

10-

Сле-

довательно,

из

миллиона

или

лаже

из ста

миллионов активных

столкновений

только одно приводит

осуществлению процесса.

175

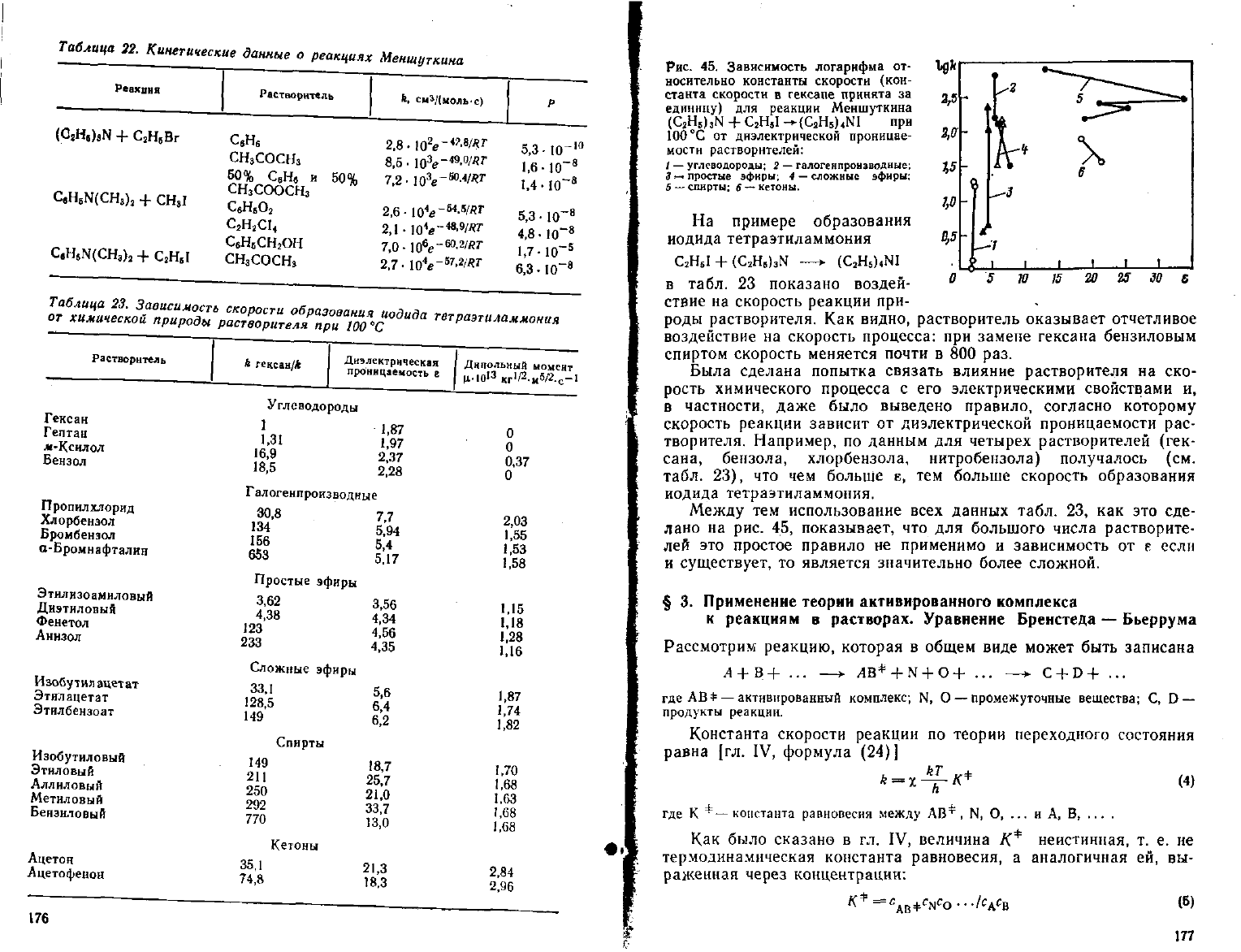
Таблица

22. Кинетические данные о реакциях Меншуткина

Реакция

N(CH

)

N(CH

)

СНзСОСНз

50%

Н«

СНзСООСНз

5,3 - 10~

4,8-10"

1,7-ИГ

6,3

•

I0~

Диэлектрическая

проницаемость

Гекеан

Гептан

.«-Ксилол

Бензол

Пропил

хлорид

Хлорбензол

Бромбензол

а-Бромнафталнп

Этнлизоамиловый

Днэтилопый

Фенетол

Анизол

Изобутилацетат

Этилацетат

Этилбензоат

Изобутиловый

Этиловый

Аллиловый

Метиловый

Бенэиловый

Ацетон

Ацетофенон

Галогенпроизводные

30,8 7 7

1£

5,4

653

Простые

эфиры

3,62

4,38

123

233

Сложные

эфиры

33,1

128,5

149

Спирты

149

211

250

292

770

Кетоны

35,1

74,8

3,56

4,34

4,56

4,35

5,6

6,4

6,2

18,7

25,7

21,0

33,7

13,0

21,3

18,3

2,03

1,55

1,53

1,58

1,15

1,18

1,28

1,16

1,87

1,74

1,82

1,70

1,68

1.63

1,68

2,84

2,96

2,5

2,0

1,0

0,5

15 20 25 30 &

Рис.

45.

Зависимость

логарифма

от-

носительно

константы

скорости

(кон-

станта

скорости

гексапе

принята

за

единицу)

для

реакции

Меншуткнна

(С

)

-*-{C

)*NI

при

100 °С от

диэлектрической

проницае-

мости

растворителей:

—

углеводороды;

2 —

галогенпроизводные;

3^ простые эфиры;

— сложные эфиры;

—

спирты;

6 —

кетоны.

На

примере образования

иодида тетраэтиламмония

),N

—>

)

в табл. 23 показано воздей-

ствие на скорость реакции при-

роды растворителя. Как видно, растворитель оказывает отчетливое

воздействие на скорость процесса: при замене гексана бензиловым

спиртом скорость меняется почти в 800 раз.

Была сделана попытка связать влияние растворителя на ско-

рость химического процесса с его электрическими свойствами и,

в частности,

даже

было выведено правило, согласно которому

скорость реакции зависит от диэлектрической проницаемости рас-

творителя. Например, по данным для

четырех

растворителей (гек-

сана, бензола, хлорбензола, нитробензола) получалось (см.

табл. 23), что чем больше е, тем больше скорость образования

иодида тетраэтиламмония.

Между

тем использование

всех

данных табл. 23, как это сде-

лано на рис. 45, показывает, что для большого числа растворите-

лей это простое правило не применимо и зависимость от е если

существует,

то является значительно более сложной.

Применение

теории

активированного

комплекса

реакциям

растворах.

Уравнение

Бренстеда

—

Бьеррума

Рассмотрим реакцию, которая в общем виде может быть записана

+ В+ ... —> .4B+ +

+ O+ ... —> C + D+ ...

гдеАВФ

—

активированный

комплекс;

N, О —

промежуточные

вещества;

С, D —

продукты

реакции.

Константа скорости реакции по теории переходного состояния

равна [гл. IV, формула (24)]

k = x-^K* (4)

где

*—константа равновесия между

АВ*

, N, О, ... и А, В, ....

Как

было сказано в гл. IV, величина /С

неистинная, т. е. не

термодинамическая константа равновесия, а аналогичная ей, вы-

раженная через концентрации:

K*=£

AB+

.../c

(б)

177