Панченков Г.М., Лебедев В.П. Химическая кинетика и катализ

Подождите немного. Документ загружается.

жают

двигаться по инерции в направлении образования конечных

продуктов. В

случае

обратимых реакций активированный комплекс

для обратной реакции имеет ту же конфигурацию, что и активиро-

ванный

комплекс исходной реакции, но противоположное направ-

ление движения вдоль координаты реакции, поэтому нельзя счи-

тать, что активированный комплекс находится в равновесии с ис-

ходными продуктами реакции. Прямой и обратный процессы с

образованием активированного комплекса протекают независимо

друг

от

друга.

Детализация теории столкновений введением состояния, про-

межуточного

между

исходным и конечным состоянием, позволила

применить к

расчету

скоростей реакций аппарат статистической ме-

ханики. Этот метод, получивший название

метода

переходного со-

стояния,

или активированного комплекса, был разработан в 1935 г.

Эйрингом и одновременно с ним Эвапсом и

Поляни.

§ 2.

Вывод

основного

уравнения

теории

активированного

комплекса

В основе теории переходного состояния

лежат

три положения:

1. Протекание реакции существенно не нарушает распределе-

ния

молекул по состояниям, так что оно

отвечает

статистически

равновесному распределению Максвелла — Больцмана. Расчеты,

на

которых мы останавливаться не

будем,

показывают, что это

справедливо для многих

случаев.

Кроме того, скорости химических

реакций,

рассчитанные по теории активированного комплекса,

согласуются

с данными опыта.

2. Элементарный акт реакции протекает адиабатически. Этот

термин в данном

случае

не имеет ничего общего с понятием ади-

абатичности в термодинамике. Он означает, что движение ядер

атомов происходит гораздо медленнее, чем движение электронов,

поэтому при каждой конфигурации ядер электроны

успевают

пере-

строиться, а их движение

успевает

принять такой характер, как

если бы ядра пребывали бесконечно

долго

в своих положениях.

Таким образом, адиабатический характер движения ядер приводит

тому,

что ядра

движутся

независимо от движения электронов,

потенциальная энергия при движении ядер изменяется непре-

рывно,

так как это движение не сопровождается электронными

переходами.

3. Движение ядер в адиабатических условиях можно рассмат-

ривать при помощи классической механики. Квантовомеханические

расчеты показывают, что это положение строго выполняется на

вершине потенциального барьера при конечной скорости движения

частицы и вблизи вершины потенциального барьера при условии

достаточно большой скорости движения частиц. Оно сильно упро-

щает решение задачи нахождения средней скорости элементарной

реакции,

так как позволяет пользоваться классической статистикой.

Как

мы увидим ниже, предположение об адиабатическом тече-

нии

элементарного химического процесса может и не выполняться,

но

как показывает опыт, такие процессы сравнительно редки

13В

Очевидно, что скорость химической реакции равна скорости

перехода

активированного комплекса через потенциальный барьер.

Выберем вдоль координаты реакции некоторый интервал конеч-

ной

протяженности длиной б, чтобы он включал вершину потен-

циального барьера. Существующая в этом интервале конфигура-

ция

атомов, изменяющаяся в сторону конечных продуктов, и яв-

ляется активированным комплексом. Среднее время жизни активи-

рованного комплекса равно:

6/с*

(4)

где

~£

— средняя скорость прохождения активированным комплексом вершины

потенциального

барьера, или, другими слопамн, среднее изменение

реакционной

координаты

со временем на вершине потенциального барьера.

Эта величина

соответствует

средней скорости движения атом-

ной

конфигурации вдоль координаты реакции и равна

сумме

ско-

ростей комплексов, переходящих через барьер, деленной на число

переходящих комплексов

<"<

c_dn

(5)

Согласно статистике Максвелла — Больцмана, число молекул,

скорость которых лежит в

пределах

и с

+ dc

, равно

dn—n

Подставляя

(6) в (5),

находим

V 2^г

ехр

(6)

(7)

Пределы интегрирования в числителе даны с

учетом,

что дви-

жение активированного комплекса осуществляется только в одном

направлении. В знаменателе же учитываются все возможные на-

правления движения.

Интеграл, стоящий в числителе, можно взять, если обозначить

J2kT = z,

тогда

dz =

2\ic

/2kT,

откуда

= kTdz/\i и,

следовательно,

кГ

—

(8)

139

Интеграл, стоящий

знаменателе, можно свести

интегралу

Пуассона. Примем \i/2kT

= h

тогда

)

ехр

dCx

+00

Обозначим

= х,

тогда

=dxjh

и \

ехр(—h

)

+00

—» -00

Но

интеграл Пуассона

поэтому

+°

Подставляя

(8) и (9) в (7),

находим

(9)

(10)

Подставляя

(10) в (4),

находим,

что

среднее время жизни

активированного комплекса равно

Обозначим концентрацию активированных комплексов,

при-

ходящуюся

на

интервал

реакционной координаты, через

Эта величина

будет

соответствовать числу возникших активиро-

ванных комплексов

или

числу актов реакций

за

время

т.

Поэтому

число актов реакции

единице объема

на

единицу времени

или,

другими словами, скорость реакции равна

w = с

/т =

б"'

(12)

Это выражение справедливо только

в том

случае, когда дости-

жение конфигурации активированного комплекса гарантирует

про-

текание реакции,

т. е., как уже

было сказано, только

для ади-

абатических процессов.

общем

случае

выражение

(12) не-

обходимо ввести

еще

добавочный множитель

—

коэффициент

про-

хождения (трансмиссионный коэффициент)

х-

который может

быть равен

или

меньше

Поэтому выражение

(12)

запишем

сле-

1ующим образом:

2зф

(13)

140

Вывод выражения

для

константы скорости

химической реакции

рассмотрим

на

примере бимолекулярной реакции

+ В —• Z —*• C + D+ ...

где

А и В —

молекулы исходных, веществ;

Z —

активированный комплекс;

С, D

т. д. —

молекулы конечных веществ.

Тогда, согласно основному

постулату

химической кинетики,

ско-

рость реакции

w=*kc

(14)

Сравнивая выражения

(13) и (14),

получим

для

константы

ско-

рости выражение

Согласно первому положению

—

применимости статистики

Максвелла

—

Больцмана

реагирующей системе

—

константа

ско-

рости элементарной реакции

A-j-B-»-C-j-D-|-...,

протекающей

при

отсутствии химического равновесия, мало отличается

от кон-

станты скорости того

же

процесса, вычисляемой

при

предположе-

нии

наличия химического равновесия

как с

конечными продукта-

ми,

так и с

промежуточными, представляющими собой активиро-

ванный

комплекс. Поэтому выражение

(15)

можно записать

в виде

А, равн

**,

равн

(16)

где индекс

«равн»

означает,

что

кониеетрацни

соответствуют

состоянию хими-

ческого равновесия.

Множитель, содержащий равров«сные концентрации, можно

за-

менить

на

константу химического равновесия исходных веществ

с конфигурацией атомов, соответстьующей активированному

ком-

плексу:

равн/

А,

равняв, равн

% С

)

Как

известно

из

статистической термодинамики, константу

рав-

новесия можно выразить через статистические суммы

соответ-

ствующих веществ

) (

при

этом энергия отсчитывается

от

нулевого.уровня соответствую-

щей молекулы

или

активированного комплекса, поэтому

соот-

ветствует

энергии активации

при

абсолютном нуле температуры.

Статистическая сумма активированного комплекса

от-

личие

от

статистической суммы стабильной молекулы содержит

виде множителя дополнительную степень свободы поступатель-

ного движения вдоль пути реакции (?

ост<1>.

Для

статистической

сум-

мы поступательного движения статистическая механика

дает

(19

141

Чтобы найти Qnocr

для

одной степени свободы, надо извлечь

из

этого выражения кубический корень, причем

для

рассмат-

риваемого случая

соответствует

интервалу пути раакции

fi. По-

этому учитывая,

что в

выражение

(18)

входят

статистические

сум-

мы,

можно написать

(20)

б/А

= Q*

(2n)LkT)

bfk

Подставляя

(21) в (18),

получим

/С*

где

(21)

(22)

(23)

можно назвать константой равновесия

между

переходным

и ис-

ходным состоянием.

действительности,

как

было сказано, такого

равновесия

нет.

Несмотря

на это, /С*

может быть рассчитана

как

обычная константа равновесия, только

из

статистической суммы

для конфигурации атомов, отвечающей активированному состоянию

(формально

при

расчете

такую

конфигурацию атомов можно

рас-

сматривать

как

молекулу), нужно исключить множитель, соот-

ветствующий движению вдоль реакционной координаты.

Подставляя выражение

(22) в (15) и

учитывая выражения

(17)

и (16),

получим

_Q*

(24)

3. Свободная энергия (энергия Гельмгольца) активации

Как

известно

из

термодинамики, константа равновесия связана

со свободной энергией процесса.

Эту

связь можно использовать

для величины

/С

вводя понятие свободной энергии активации,

характеризующей изменение свободной энергии

при

переходе

сис-

темы

из

исходного состояния

активное

учитывающей

все сте-

пени

свободы, кроме координаты реакции. Если вещества нахо-

дятся

стандартном состоянии,

то для

процесса, протекающего

при

постоянном объеме

ЯГ1пДГ*

(25)

так как

выражение (25)

можно записать

К*

= схр

(AS*//?)

exp (-

AU/RT)

Подставляя

это

выражение

в (24),

получим

{26)

(27)

Соответственно, если процесс протекает

при

постоянном давле-

1ии, надо пользоваться изобарным потенциалом (свободной

энер-

гией

при

постоянном давлении, энергией Гиббса). Аналогичные

тссуждения приводят

выражению

для

константы скорости.

(29)

В этих выражениях

Д£/* и ДЯ*

имеют физический смысл

теп-

[лот активации,

a AS*

—энтропии активации.

Выражения

(27) и (28)

формально похожи

на

выражение,

по-

рученное нами полуэмпирически

в гл. III, но

теперь стерический

[множитель приобретает вполне определенный смысл.

Как

будет

!показано

ниже,

Д£/+ и ДЯ*

связаны

энергией активации, опре-

деляемой опытным путем,

и,

следовательно, множитель, содержа-

щий

энтропию активации

AS+,

соответствует

стерическому

мно-

жителю теории столкновений.

Из

уравнений (27) —(29) вытекает,

что скорость реакции определяется

не

теплотой активации,

а из-

менением свободной энергии

при

переходе

системы

активное

состояние. Если

переход

соответствующее состояние сопровож-

дается большим увеличением энтропии,

то,

несмотря

на

высокое

значение энергии, реакция

будет

протекать

большой скоростью.

Наоборот, процессы, сопровождающиеся уменьшением энтропии,

несмотря

на

малую

теплоту активации

Д//*,

будут

протекать

мед-

ленно.

Любой внешний фактор, уменьшающий свободную энергию

активации,

будет

способствовать увеличению скорости химиче-

ского процесса. Таким образом, название «стерический множи-

тель»,

как

видно,

не

соответствует

физическому смыслу этой

ве-

личины,

поэтому

ее

лучше

называть «энтропийный множитель».

Иногда

ее

называют «вероятностным фактором».

Экспериментальная энергия активации

В выражения

(28) и (29)

входят

не

экспериментально определяе-

мые энергии активации,

изменения внутренней энергии или тепло-

содержания

при

переходе

исходных молекул

состояние активи-

рованного комплекса.

Для практических расчетов было

бы

более интересным ввести

эти

выражения экспериментально определяемую энергию

ак-

тивации.

Если

качестве независимых переменных выбрать давле-

ние

температуру,

то

удобным выражением

для

расчета

ско-

рости реакции

будет

выражение

(24).

Прологарифмировав

вы-

ражение

(24),

находим:

х +

(k/h)

Г +

Л'* (30)

Дифференцируя

это

выражение

по

температуре

принимая

во

внимание

уравнение Аррениуса, получим:

dlnK

_ _L _i_ _!!£_

ЦТ* dT T '

где

—

экспериментальная

энергия

активации.

143

(31)

143

Принимая

во внимание, что согласно уравнению изобары хими-

ческой реакции

(32)

(33)

выражение (31) можно записать

откуда

=RT+bH*

(34)

Так

как для идеальных газов ДЯ* не зависит от давления, эта

величина в рассмотренных уравнениях не отнесена к стандарт-

ному состоянию. Для выбранного стандартного состояния выраже-

ние

(29) приобретает вид

кТ

(35)

Подставляя значение АН* из выражения (34) в (35), получим

кТ

(36)

Если

удельная скорость выражена в единицах концентрации,

то,

принимая во внимание, что

*(У

(37)

{х — число молекул, входящих в активированный комплекс) по-

лучаем

k =

(RT)*-

(38)

Для процесса, протекающего при постоянном объеме, анало-

гично выражению (31), получим

экси

^dlnk

I din К*

2 e

dT T •* dT ^

откуда

ЭКСп

«= RT + AU* = RT + ДЯ* —

pAV*

(40)

где AV'f — изменение объема при переходе в активное состояние.

Для реакции, протекающей в газовой фазе, при условии, что

газы идеальны

Подставляя это выражение в (40), получим

(x-\)RT

(42)

(43)

Подставляя (38) и (42) в (36),

будем

иметь

к-

144

случае

растворов стандартное состояние соответствует кон-

центрации

(или активности), равной единице, поэтому уравнение

(29) надо записать в виде

кТ

дя+Л

)

(44)

где указание на стандартное состояние ДЯ* опущено, так как при-

нимается,

что система идеальна. Поскольку в

случае

растворов

AV практически равно нулю, легко видеть, что выражение (43)

запишется в виде:

expi

(45)

5. Взаимодействие

двух

атомов.

Сравнение

теории столкновений

с теорией активированного комплекса

Рассмотрим расчет скорости реакции взаимодействия

двух

атомов

по

теории переходного состояния. Пусть массы атомов

будут

пгк и

, а их эффективные радиусы — г

и гв. Активированный ком-

плекс

в этом

случае

будет

аналогичен двухатомной молекуле АВ.

Суммы состояний для атомов, обладающих только тремя поступа-

тельными степенями свободы, равны

(46)

Активированный комплекс обладает тремя поступательными

(учет

одной из которых, соответствующей перемещению ком-

плекса по координате реакции, привел к появлению множителя

kT/h)

и двумя вращательными степенями свободы. Его сумма

состояний

равна

+ =

АП

Момент инерции активированного комплекса

ГП \ГП

(47)

(48)

где ГА +гв — диаметр активированного комплекса.

Подставляя (48) в (47), находим

Г2я (mi + т,Л кГ\

8л'т

кТ

145

Зная

статистические суммы, можно рассчитать константу ско-

рости реакции. Подставляя выражение (23) в (24), найдем

Для простоты положим, что

= 1 и В

= 0,

тогда,

подставляя

выражение (50) значения статистических сумм (46) и (49), по-

лучим, что число сталкивающихся (реагирующих) молекул в еди-

ницу

времени в единице объема равно

(51)

Согласно теории столкновений число сталкивающихся молекул

единицу времени в единице объема при условии пл=^пв = 1

равно

АВ

(52)

Принимая

во внимание, что

получаем выражение

(53)

которое совпадает с выражением, полученным по теории активи-

рованного комплекса (51). Таким образом, для взаимодействия

двух

атомов теория столкновений приводит к одинаковому резуль-

тату

с теорией активированного комплекса.

Рассмотрим, совпадут ли результаты расчетов скоростей реак-

ции

методом теории столкновений с результатами теории пере-

ходного состояния в случае, если реагируют не атомы, а молекулы.

Для решения этого вопроса упростим

задачу,

приняв, что для

каждого вида энергии сложной молекулы сумма состояний скла-

дывается из одинаковых множителей, по одному на каждую сте-

пень

свободы. Обозначив через q

^, </вр

щ и <у

ил соответственно

поступательную, вращательную и колебательную суммы состоя-

ний

на одну степень свободы, для полной суммы состояний по-

лучим

?пост

;

?вращ'?кол

'54)

где t, r и v — соответствующие числа степеней свободы.

Для только что разобранного случая реакци,

^томами

суммы состояний находящихся в равновесии частиц равны

(

140

предэкспоненциальный член в уравнении (50) для константы

скорости реакции выразится соотношением

кТ

ОЛ*Ф

q'i

nam

(56)

вращ

ЧЦОСГ

QAQB

Но,

как было показано, это выражение

дает

число столкнове-

ний

атомов А с В в единицу времени в единице объема при усло-

вии,

что ПА = /1в = !, т. е.

^=(^/А)<7

вря

„>

ОС

(

Для нелинейных многоатомных молекул А и В, состоящих из

ПА

И п

атомов, суммы состояний имеют вид

Яп~

Зп"

О.=/7

.._о

alA и С =

^„„^„„„«/.гЛ

(58)

а для активированного комплекса, имеющего на одну колеба-

тельную степень свободы меньше по сравнению с молекулой, со-

стоящей из такого же количества атомов

- -L .3 _3

„3(ш

ПВ

)-7

(5д

(60)

(61)

Тогда предэкспоненциальный член

(50)

равен

kT д

АВ

^ kT gl^

h qi

0CT

pailK

или,

принимая во внимание выражение (57) имееу

Таким

образом, для взаимодействия

двух

нелинейных много-

атомных молекул (для

других

типов превращений получаются

несколько

отличные выражения) теория активированного ком-

плекса

дает

значение константы скорости, отличающейся на мно-

житель (<7кол/<7вращ)

, от значения константы скорости, даваемого

теорией столкновений — уравнение (53). Поэтому ранее введен-

ный

стерический множитель, согласно рассматриваемой теории,

оказывается равным

«*

(</кол/<7пр

а1

ц)

(62)

Поскольку

сумма состояний для колебательной энергии близка

единице, а порядок вращательной суммы состоянии лежит в пре-

делах

от 10 до 10

, крайние значения стерического фактора, со-

гласно этому приближенному соотношению, образуют интервал

Ю~

—10~

Этот множитель, поскольку он связан с энтропией,

иногда называют «вероятностным фактором».

6. Неадиабатические процессы.

Трансмиссионный

коэффициент

Как

было показано, в

случае

адиабатических процессов

коэффи-

циент

прохождения (трансмиссионный коэффициент) %=\. Элемен-

тарные процессы, сопровождающиеся электронными переходами,

147

Рис.

38. Адиабатический (а) и

пеадиабатиче-

скин

(б) ход процесса в области наибольшего

сближения

двух

потенциальных кривых.

являются неадиабатическими. Элек-

тронный переход

соответствует

перехо-

ду системы при достижении вершины

барьера с одной потенциальной по-

верхности на

другую

(рис. 38; г —

межатомное расстояние).

При

неадиабатическнх процессах

достижение вершины потенциального

барьера еще не означает безусловного

перехода к конечным продуктам и

существует

конечная вероятность

перехода системы с нижней потенциальной поверхности на верхнюю.

Таким образом, для неадиабатических процессов трансмиссионный

коэффициент

х заведомо меньше единицы. Как правило, неадиаба-

тическое течение процесса имеет место, если реакция приводит к

изменению суммарного электронного спина или к какому-нибудь

другому

запрещенному

переходу.

Трансмиссионный коэффициент

для неадиабатических процессов чаще всего оказывается порядка

10~

. Приближенные расчеты показывают, что неадиабатические

реакции

встречаются довольно редко.

Таким образом, теория активированного комплекса в том слу-

чае, когда известна конфигурация реагирующих молекул в пере-

ходном состоянии, позволяет рассчитать предэкспоненциальный

множитель. Но в большинстве случаев, к сожалению, строение

активированного комплекса и его свойства бывают неизвестными.

Структура соединения, представляющего переходное состоя-

ние,

согласно

постулату

Хеммонда для сильно экзотермических

реакций

близка к строению исходных молекул, а для сильно эндо-

термических реакций близка к

структуре

конечных продуктов.

Этот постулат

лучше

выполняется для мономолекулярных реак-

ций.

Для бимолекулярных реакций он выполняется плохо, так как

изменение энергии Гиббса в этом

случае

обусловлено в основном

уменьшением энтропии, а не энтальпии реакции перехода системы

в конечное состояние.

Иногда теорию активированного комплекса называют

теорией

абсолютных

скоростей

реакций.

Но такое название неправильно,

так как для расчета абсолютных скоростей химических реакций

надо иметь возможность рассчитать не только предэкспоненциаль-

ные множители, но и энергии активации. Теоретический расчет

энергий активации можно осуществить лишь методами квантовой

механики. Однако последние пока малопригодны для получения

количественных результатов.

Несмотря на указанные недостатки, теория переходного со-

стояния

позволяет получать качественные результаты, интересные

для понимания протекания химических процессов. Применение

этой теории для выяснения характера протекания некоторых хи-

мических процессов

будет

рассмотрено в последующих

главах.

148

ГЛАВА

МОНОМОЛЕКУЛЯРНЫЕ

И ТРИМОЛЕКУЛЯРНЫЕ

РЕАКЦИИ

Мономолекулярные

реакции

газовой

фазе

В настоящее время известно большое число гомогенных газовых

реакций,

удовлетворяющих кинетическим уравнениям первого по-

рядка.

Кроме указанных в гл. I реакций разложения азометана, пента-

оксида азота, диметилового эфира к ним относится разложение

тетраалкилов элементов IV группы Периодической системы, на-

пример,

тетраметилолова

Sn(CH

—> Sn + 4.CH

разложение некоторых алифатических галогенпроизводных, на-

пример,

2-хлорпропана

—-*•

СН

СН=СН

цис-транс-превращения производных этилена, например, малеино-

вой кислоты

НС—СООН

НООС—СН

ис—соон

НС—СООН

термическое превращение различных органических молекул, на-

пример,

этилбензола

2С

СН

—•

+ С,Н„

термический распад диазосоединений, например, диазопропана

распад альдегидов, например, пропилового

—*

некоторые

другие

реакции. Мономолекулярный распад претерпе-

вают, как правило, сложные молекулы, состоящие из большого

числа атомов; энергии активации большинства реакций относи-

тельно высоки (табл. 14).

При

низких давлениях для большинства мономолекулярных

реакций

наблюдается интересное явление перехода реакции в ре-

акцию второго порядка. Так, для термического разложения изо-

пропилхлорида при давлениях выше 0,53 кПа константа скорости

первого порядка не зависит от начального давления и сохраняет

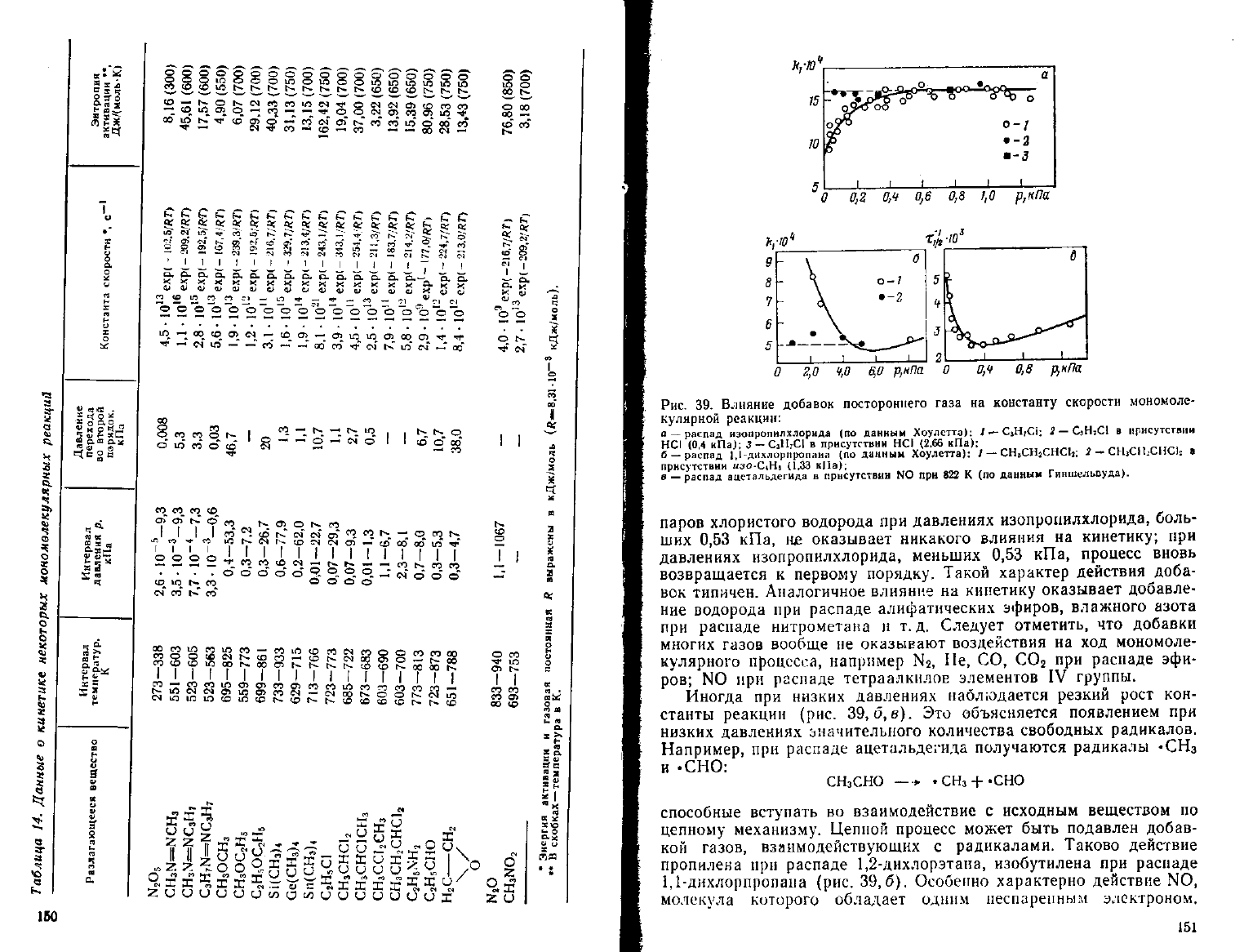
постоянное значение. Однако, как видно из рис. 39, а, при давле-

ниях ниже 0,53 кПа значение константы скорости систематически

уменьшается и процесс явно перестает удовлетворять кинетиче-

скому уравнению первого порядка. Интересно, что добавление

149

а-

ISO

5 si

fSfI.3

О!

а!

OOOOOOOO

оюрооюою

NWrtrtin

^ л - —

о о о

о ю m ю

N Й (D (О

о о

о;

а: ос сц а? а;

еч m

С - С С

to * rt

—

ч р; ?!

U-)

_ оз —

•«• п

о. а а о. S 5, а

****»-:«ХК

(С Ю П

____•

— U1 Ч-

О О О О О О "о

о.

о.—• о. а.

х Й- к х

—. — _ _ ^

ОООООООО

—

»(£>о>с<

—

tool

— е?>

— СЧ Ю* —" — СО* —" — ОО" СО*

О1_

•* Т

ьГ 1Л*

сч"

—

оо"

Ю СО О

(О

S О

ГО — f. —•

О - - о -

t--_

h-, О

о" со

—

:о

в!

О N П

I I I

О О

сч

со г-*

со*

*Г

СО СО СО CN

о о о о о

I I I I I I I

— — со

Я °. Я —

<N"

О О О

со

о о о

«OlDiftgO

I I I I

—

CO CO Ю

hlOCNCNCJ

CJi

сосоиЬсоэтсососо

—

X •*

2: ?:

4x x tix

•z.

и •• •

и и

«о

аи"

О д

•*

!N*

]

со

во

СО

СП

•

»ur

к,-ю

2,0 4,0 6,0

р,чПа

0 0,4 0,8

р,кПп

Рис.

39.

Влияние добавок постороннего

газа

на

константу скорости мономоле-

кулярной реакции:

—

распад изопропилхлорида

(по

данным

Хоулетта):

—

CsH,Ci;

—

CjHjCl

присутствии

HCI

(0.4

кПа);

3 -

СМ,С\

присутствии

НС1 (2.66

кПа);

—

распад

1,1-дихлирпропана

(поданным

Хоулетта):

—

CHJCHJCHCIJ:

—

CHJCUJCHCIS

присутствии ujo-C.Hs

(1.33

к11а);

—

распад

ацстальдегида

присутствии

при

822 К

(по

данный Гиншельоуда).

паров

хлористого водорода

при

давлениях изопропилхлорида, боль-

ших

0,53

кПа,

не

оказывает никакого влияния

на

кинетику;

при

давлениях изопропилхлорида, меньших

0,53

кПа,

процесс вновь

возвращается

первому порядку. Такой характер действия доба-

вок

типичен. Аналогичное влияние

на

кинетику оказывает добавле-

ние

водорода

при

распаде алифатических эфнров, влажного азота

при

распаде нитрометана

и т.д.

Следует отметить,

что

добавки

многих газов вообще

не

оказывают воздействия

на ход

мономоле-

кулярного процесса, например

N2, Не, СО, СОг

при

распаде

эфи-

ров;

N0 при

распаде тетраалкилов элементов

группы.

Иногда

при

низких давлениях наблюдается резкий рост

кон-

станты реакции

(рис. 39,

(5,в).

Это

объясняется появлением

при

низких

давлениях значительного количества свободных радикалов.

Например,

при

распаде

цет

льде гида получаются радикалы «СН

.СНО:

СНзСНО

—*

.СНз-f-'CHO

способные

вступать

во

взаимодействие

исходным веществом

по

цепному

механизму. Цепной процесс может быть подавлен добав-

кой

газов, взаимодействующих

радикалами. Таково действие

пропилена

при

распаде 1,2-дихлорэтана, изобутилена

при

распаде

1,1-дихлорпропана (рис. 39,6). Особенно характерно действие

NO,

молекула которого обладает одним иеспарепным электроном.

151

При

столкновении со свободным радикалом N0 легко к нему при-

соединяется, обрывая цепь, и значение константы скорости стано-

вится соответствующим истинному мономолекулярному распаду

(рис.

39,е). На оси ординат ту, —время полураспада).

Ранние

теории

мономолекулярных

реакций

Скорость

реакции первого порядка прямо пропорциональна давлению (или

концентрации)

в первой степени. Между тем, согласно ранее рассмотренным

механизмам,

активация молекул достигается путем столкновения, число же

столкновений

прямо пропорционально квадрату давления (илн концентрации).

Таким

образом, на первый взгляд кажется, что столкновения не являются при-

чиной

мономолекулярного процесса. Отсюда

понятно,

что первые попытки дать

теоретическое

истолкование мономолекулярных реакций основывались на по-

исках

причин активации молекул, не зависящих от столкновений.

Первой

такой попыткой была гипотеза Перрена (1918 г.), согласно которой

активация

при мономолекулярных реакциях происходит за счет поглощения ин-

фракрасной

радиации. Эта гипотеза не выдержала опытной проверки, так как

оказалось,

что облучение реагирующей системы потоком квантов с частотой,

соответствующей

энергии активации (v =

E/hN),

не изменяет скорости процесса.

1924 г. Христиансен и Крамере пытались объяснить активацию в

моно-

иолекулярном

процессе столкновением исходных молекул с богатыми энергией

продуктами

реакции. Однако и это объяснение противоречило опыту, поскольку,

во-первых,

существуют эндотермические мономолекулярные реакции (например,

распад

N2O5) н, во-вторых, как выше было показано, мнорие посторонние газы

не

оказывают воздействия на ход процесса, между тем, дезактивируя продукты

реакции,

они должны были бы систематически снижать скорость реакции.

Истолкование

мономолекулярных

реакций

на

основании

теории

столкновений

В 1922 г. Линдеман дал

схему,

позволяющую понять механизм

мономолекулярных реакций, исходя из представлений о столкнове-

нии

молекул. Для того чтобы произошел мономолекулярный про-

цесс распада молекулы А, ей необходимо обладать достаточной

колебательной энергией для разрыва связей. Эту энергию моле-

кула может накопить путем соударений, т. е. процесс активации

молекулы можно записать в виде

А + А -X А* + А

где А* — возбужденная молекула.

Наряду с процессом активации в

результате

столкновений про-

исходит и дезактивация

А'

А+А

Оба эти процесса поддерживают равновесную концентрацию

активных молекул [Л*], соответствующую распределению Макс-

велла — Больцмана. В отсутствие химической реакции доля актив-

ных молекул не зависит от давления (концентрации), а число их

прямо пропорционально давлению (концентрации), поскольку с

изменением давления пропорционально изменяются и скорости ак-

тивации, и скорость дезактивации. При наличии химической реак-

152

ции

убыль концентрации активных частиц происходит и в резуль-

тате

процесса их распада

А*

Продукты

реакции

При

установившемся процессе постоянство концентрации активных

молекул определяется условием:

скорость активации = скорость дезактивации + скорость реак-

ции,

т. е.

МА]

ЫА][А']

+ ЫА'] U)

откуда

IA1»

а скорость реакции

[А']

д\А]

[A]

(2)

(3)

Активные молекулы А* имеют определенное время жизни тд«,

связанное с вероятностью превращения А* в конечные продукты.

В зависимости от соотношения т

*, и времени

между

столкнове-

ниями

тст уравнение (3) может быть представлено в

двух

предель-

ных формах.

При

высоких давлениях столкновения настолько часты (т

ст

«с

«С т

-), что почти все молекулы А* дезактивируются, не успевая

прореагировать, т.е. k

[A] *С &з, и

а [А] Ыз

»_,

А1 т

таким образом, реакция является процессом первого порядка.

понижением давления время

между

столкновениями воз-

растает и может превысить время жизни активной молекулы (т

ст

^> тд«). Тогда большая часть молекул, не успевая дезактивиро-

ваться, претерпевает превращение, т. е. k$ > &г[А] и

*,[А]

(5)

что

соответствует

процессу второго порядка.

Таким образом, схема Линдемана позволяет объяснить как

механизм активации, так и причины перехода мономолекулярных

реакций

при низких давлениях в реакции второго порядка.

Скорость —

d[A]/dt

мономолекулярной реакции, согласно ос-

новному

постулату

химической кинетики, можно записать в виде:

-к

[А] (6)

где ft —константа скорости, определяемая из опыта.

Сравнивая выражения (6) и (3), находим

ИЛИ

*![А] +

кг

[AJ

(8)

7,5 15,0 22,5

ЩмПг*

Рис.

40. Зависимость константы скорости мономолекулярной реакции от началь-

ного

давления:

а—разложение диннтрокснда

(по

данным Фольмера»,

938 К. *

'=522

8,76-10

оа

—1.92-10

-3

с~';

б—распад диазометана

(по

данным Рамспергера).

603 К. ft"*' =

3,7В-10

р-

№

—в.И-Ю-*^

Заменяя

[А] через р

= [A]RT и

/*i*s

= 1/А», получаем

1 .

const

(9)

где, как легко видеть, const = RT/k\.

Таким

образом, в координатах й-

—рд должна получиться

линейная

зависимость, позволяющая вычислить предельную кон-

станту при больших (формально при

р-*-<х>)

давлениях. Есть

экспериментальные примеры выполнения этой зависимости

(рис.

40, а), но значительно чаще линейная зависимость иска-

жается и точное вычисление £« затруднительно (рис. 40, б) *.

Если

исходить из

схемы

Линдемана, то

между

мономолекуляр-

ными

и бимолекулярными реакциями нет принципиальной разницы.

В зависимости от условий (температуры, давления) и свойств

реагирующей системы (времени жизни активного состояния) лю-

бой процесс, активируемый двойными столкновениями, может

идти как по первому, так и по второму порядку. При этом ско-

рость мономолекулярной реакции не может превышать скорости

активации,

т. е. бимолекулярного процесса. Таким образом, при-

няв

тот или иной вид для функции распределения /(£), например

распределение Максвелла — Больцмана для системы с

двумя

сте-

пенями

свободы, казалось бы можно вычислить предельно воз-

можную скорость мономолекулярной реакции: **

да

пред

,-EtRT

(10)

* Приведенная на рис. 40,6 линейная экстраполяция из области малых дав-

лений,

строго говоря, неверна, хотя и используется нередко в оригинальной ли-

тературе. Дело в том, что нельзя пользоваться значением константы при малых

давлениях, так как в этой области мономолекулярный характер процесса наи-

более искажен. Экстраполяцию можно проводить только в области высоких

давлений,

как это показано на рисунке точками.

•* Уравнение (10)

дает

число активных двойных столкновений, выражен-

ное

в моль/см

(си. гл. III).

154

Рассмотрим для этого разложение этилхлорида при 13 332 Па

(100 мм рт. ст.) и 750 К. В 1 см

при этих условиях содержится

100-0,001

2,14-10

моль С

С1

760-0,821-750

Из

данных табл. 14 получаем:

w = 3,9 -10

2,14 • 10~

ехр (- 254

400/8,314

• 750) =

3,9 • 10

• 2,14 • 10~

• 1,9 • 10~

= 1,59 • 10~

моль/(с • см

)

Между

тем предельная скорость не должна превышать

Х(2,14-

Ю"

)

. 1,9- 10~

= 3,

моль/(с-см

)

Таким

образом, опытная скорость в

1,59-10-

/3,13-10-

5.09Х

X Ю

раз превышает предельную вычисленную. Аналогичные ре-

зультаты

получаются и для

других

мономолекулярных реакций.

4. Энергия активации мономолекулярной реакции

Если

считать, что мономолекулярная реакция протекает настоль-

ко

медленно, что распределение Максвелла — Больцмана не на-

рушается, то число молекул, энергия которых равна е/, опреде-

лится выражением

где Л( — число молекул, энергия которых равна или более е.г, п — общее число

молекул; Q — статистическая сумма; gi — статистический вес данного состояния.

Статистическая

сумма

равна

В рассматриваемом

случае

энергия ti как соответствующая

колебательной энергии молекулы квантована.

Если

бы молекулы в каждом активированном состоянии реаги-

ровали со скоростью А(е,-), то суммарная скорость реакции, обу-

словленная всеми активированными молекулами, была бы равна

Подставляя в выражение (11) значение т, получим ,

(12)

откуда константа скорости мономолекулярной реакции

= —

(13)

Логарифмируя

выражение (13), получаем

к = In £ * ff, exp (- ejkT)

—

откуда

dlnfe

exp

(15)

Легко видеть, что первое слагаемое есть средняя энергия ак-

тивных молекул

акт

деленная на kT

, а второе слагаемое —ана-

логичная величина для

всех

молекул. Поэтому выражение (15)

можно записать в следующем виде:

dink

^зкт

—

kT ~

—

(16)

По

внешнему виду это уравнение похоже на уравнение Аррениуса.

Следовательно, и для квантованных систем справедливо уравне-

ние

Аррениуса. Из выражения (16) видно, что энергия активации

мономолекулярной реакции равна разности средней энергии ак-

тивных молекул и средней энергии

всех

молекул.

б. Теории Гиншельвуда, Касселя, Слетера

Гиншельвуд первым обратил внимание на необходимость

учета

внутренних степеней свободы молекулы, претерпевающей моно-

молекулярный распад. В его теории и еще более отчетливо во

всех

последующих теориях учитываются колебательные составляющие

внутренней энергии молекулы: молекула рассматривается как со-

вокупность s осцилляторов.

Теория

Гиншельвуда основана на

двух

положениях.

1. Молекула становится способной к мономолекулярному рас-

паду только в том случае, если на

всех

колебательных сте-

пенях

свободы молекулы сосредоточится некоторая критиче-

ская

энергия е

. Существенно, что не делается какого-либо

предпочтения для сосредоточения определенной доли

энер-

гии

на некоторой избранной степени свободы.

2. Достижение суммарной энергии е

является необходимым

достаточным условием для активации. Различия в реак-

ционной

способности молекул, обладающих любым избыт-

ком

энергии г.о сравнению с е

вплоть до оо, не рассматри-

ваются.

156

Можно

показать, что число активных молекул, даваемое тео-

рией

Гиншельвуда, равно

1)!

(E/RT)

е~

(17)

где 5 — число колебательных степеней свободы.

Все активированные молекулы (по Гиншельвуду) обезличены,

поэтому константа скорости реакции k

, независимо от значения

е/, равна некоторой постоянной величине Я.

Скорость

реакции при больших давлениях равна

An,

--EIRT

(18)

Уравнение (18) отличается от выражения, даваемого теорией

столкновений,

на множитель (E/RT)

/(s—1)!

Теория

Гиншельвуда

дает

хорошее согласие с опытными значе-

ниями

скоростей реакции для ограниченного набора колебательных

степеней свободы, но полный

учет

колебательных степеней свободы,

например,

в реакции термического распада этилхлорида, рассмот-

ренной

нами ранее, приводит к неправдоподобно большому теорети-

ческому значению скорости. Объясняется это тем, что, вероятно, не

все степени свободы принимают участие в активации молекулы,

ибо разрыв обычно происходит по небольшому числу связей —

чаще всего одной. При этом, если отвлечься от произвола в выборе

числа степеней свободы,

участвующих

в активации, при проверке

соответствия теории и опыта возникает серьезное противоречие.

Если

только немногие степени свободы

участвуют

в активации, то

должна быть учтена вероятность сосредоточения энергии на этих

степенях свободы. Эта вероятность в

случае

разрыва одной связи

имеет значение порядка

10~

—10~

Ее

учет

свел бы на нет согласие

теории Гиншельвуда с опытом.

Дальнейшее развитие теории мономолекулярных реакций шло

по

линии уточнения понятия активированной молекулы. Очевидно,

молекула, обладающая энергией, равной или большей е», не всегда

способна к мономолекулярному превращению. Активны только те

молекулы, у которых избыток энергии концентрируется на опреде-

ленных связях. Этот факт учитывается в теориях Касселя (1932 г.)

Слетера (1939 г.).

В теории Касселя молекула рассматривается как совокупность

s гармонических осцилляторов, обладающих одинаковой постоян-

ной

частотой колебания v и, следовательно воспринимающих и

отдающих энергию, кратную энергии кванта hv. Число гармониче-

ских осцилляторов принимается равным числу колебательных сте-

пеней

свободы. Для нелинейной /^-атомной молекулы

= ЗА —5 (19)

Активной молекулой

будет

такая, у которой на одном опре-

деленном осцилляторе сосредоточено число квантов, равное т.

157