Ответы по физике
Подождите немного. Документ загружается.


Рассмотрим две волны, распространяющиеся от точечных источников О
1
и О
2
,
колеблющихся с постоянной разностью фаз (такие источники называются, как и порождаемые
ими волны, когерентными). Определим результирующее колебание в какой-либо точке среды
при условии, что оба колебания, вызываемые каждой из волн в отдельности, имеют
одинаковое направление.
Пусть фазы колебаний источников О
1
и О
2
равны
соответственно (
t +
1
) и (
t +
2
). Тогда колебание в
данной точке будет равно сумме колебаний:
1 1 1 1
2 2 2 2
cos( )
cos( )
a t kr
a t kr
,
где а
1
и а
2
– амплитуды волн в рассматриваемой точке, k –
волновое число, r
1
и r
2
– расстояния от источников волн до
данной точки.
В точках, определяемых условием
1 2 1 2
( ) ( ) 2 ( 0,1,2,...)k r r n n
(83.1)
колебания волн синфазны, следовательно, усиливают друг друга и результирующее движение
представляет собой гармоническое колебание частоты
с амплитудой |а
1
+ а
2
|.
В точках, для которых
1 2 1 2
1
( ) ( ) 2 ( 0,1,2,...)
2
k r r n n
(83.2)
колебания противофазны, ослабляют друг друга, и результирующее движение является
гармоническим колебанием с амплитудой, равной |а
1
– а
2
|. В частном случае, когда а
1
= а
2
,
колебания в этих точках будут отсутствовать.
Условия (83.1) и (83.2) сводятся к тому, что разность r
1
– r
2
постоянна:
1 2
constr r
(83.3)
Из аналитической геометрии известно, что уравнение (83.3) есть уравнение гиперболы с
фокусами в точках О
1
и О
2
. Таким образом, геометрические места точек, в которых колебания
усиливают или ослабляют друг друга, представляют собой семейство гипербол. На рис.201,
изображены эти гиперболы для случая
1
–
2
= 0. Сплошными линиями указаны места, в
которых колебания усиливают друг друга, пунктирными – места, в которых колебания
ослабляют друг друга.
Волны, встретив на своем пути препятствие, огибают его. Это явление называется
дифракцией. Возникновение дифракции можно объяснить с помощью принципа Гюйгенса,
которым устанавливается способ построения фронта волны в момент времени t + t по
известному положению фронта в момент времени t.
Согласно принципу Гюйгенса каждая точка, до которой доходит волновое движение,
служит центром вторичных волн; огибающая этих волн дает положение фронта волны в
следующий момент.
Пусть на плоскую преграду с отверстием падает параллельный ей фронт волны (рис. 203).
По Гюйгенсу каждая точка участка волнового
фронта, выделяемого отверстием, служит центром
вторичных волн, которые в однородной и
изотропной среде будут сферическими. Построив
огибающую вторичных волн, мы убеждаемся в
том, что за отверстием волна проникает в область
геометрической тени (на рисунке границы этой
области показаны пунктиром), огибая края преграды.
Стоячие волны
Рис. 201.
Рис. 203.
11
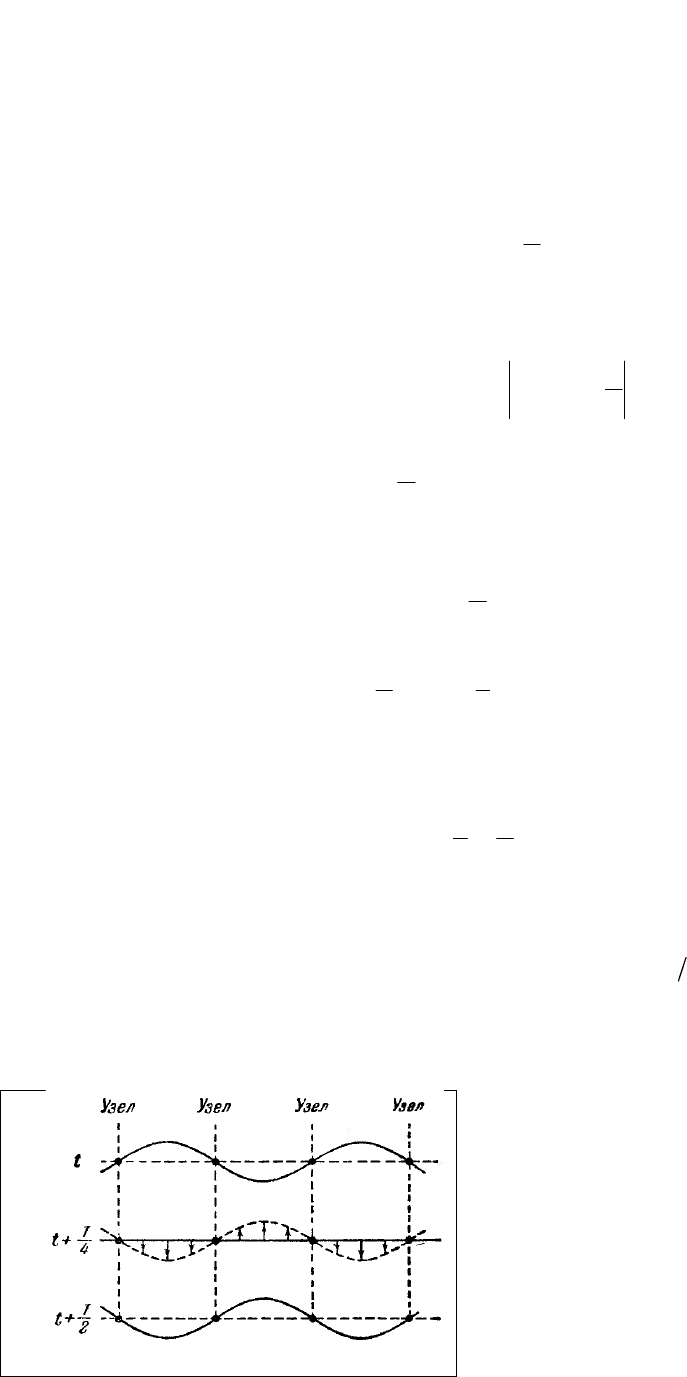
Очень важный случай интерференции наблюдается при наложении двух встречных
плоских волн с одинаковой амплитудой. Возникающий в результате колебательный процесс
называется стоячей волной. Практически стоячие волны возникают при отражении волн от
преград. Падающая на преграду волна и бегущая ей навстречу отраженная, налагаясь друг на
друга, дают стоячую волну.
Напишем уравнения двух плоских волн, распространяющихся в противоположных
направлениях:
1
2
cos( )
cos( )
a t kx
a t kx
Суммировав уравнения и преобразовав результат по формуле для суммы косинусов,
получим:
1 2
2 cos cosa kx t
Заменив волновое число k его значением 2
/
, выражению для
можно придать
следующий вид:
(2 cos2 ) cos
x
a t
(84.1)
Уравнение (84.1) и есть уравнение стоячей волны. Из него видно, что в каждой точке
стоячей волны происходят колебания той же частоты, что и у встречных волн, причем
амплитуда оказывается зависящей от х:
àì ï ëèòóäà 2 cos2
x
a
В точках, где
2 ( 0,1,2,...)
x
n n
(84.2)
амплитуда колебаний достигает максимального значения 2а. Эти точки называются
пучностями стоячей волны. Из условия (84.2) получаются значения координат пучностей:
ï ó÷í
( 0,1,2,...)
2
x n n
(84.3)
В точках, где
1
2 ( 0,1,2,...)
2
x
n n
амплитуда колебаний обращается в нуль. Эти точки называются узлами стоячей волны.
Точки среды, находящиеся в узлах, колебаний не совершают. Координаты узлов имеют
следующие значения:
óçë
1
( 0,1,2,...)
2 2
x n n n
(84.4)
Из формул (84.3) и (84.4) следует, что расстояние между соседними пучностями, как и
расстояние между соседними узлами, равно
/2. Пучности и узлы сдвинуты друг относительно
друга на четверть длины волны.
Обратимся снова к уравнению (84.1). Множитель
2 cos(2 )a x
при переходе через
нулевое значение меняет знак. В соответствии с этим фаза колебаний по разные стороны от
узла отличается на
, т. е. точки, лежащие по разные стороны от узла, колеблются в
противофазе. Все точки, заключенные между двумя соседними узлами, колеблются синфазно
(т. е. в одной и той же фазе). На рис. 204 дан ряд
«моментальных фотографий» отклонений
точек от положения равновесия. Первая
«фотография» соответствует моменту, когда
отклонения достигают наибольшего абсолютного
значения.
Рис. 204.
12

Последующие «фотографии» сделаны с интервалами в четверть периода. Стрелками
показаны скорости частиц.
Продифференцировав уравнение (84.1) по х и t, мы найдем закон, по которому изменяется
деформация среды
и и скорость частиц
:
2
2 sin 2 cos
x
a t
x
(84.5)
2 cos2 sin
x
a t
t
(84.6)
Уравнение (84.5) описывает стоячую волну деформации, а
(84.6) – стоячую волну скорости. Из вида этих уравнений
следует, что узлы и пучности скорости совпадают с узлами и
пучностями смещения; узлы же и пучности деформации
совпадают соответственно с пучностями и узлами скорости и
смещения (рис. 205). В то время как
и
достигают
максимальных значений,
обращается в нуль, и наоборот.
Соответственно дважды за период происходит превращение
энергии стоячей волны то полностью в потенциальную,
сосредоточенную в основном вблизи узлов волны (где находятся
пучности деформации), то полностью в кинетическую,
сосредоточенную в основном вблизи пучностей волны (где
находятся пучности скорости). В результате происходит переход
энергии от каждого узла к соседним с ним пучностям и обратно.
Средний поток энергии в любом сечении волны равен нулю.
Эффект Доплера
Пусть в упругой среде на некотором расстоянии от источника волн располагается
устройство, воспринимающее колебания среды, которое мы будем называть приемником.
Когда источник и приемник волн неподвижны относительно среды, в которой
распространяется волна, то частота колебаний, воспринимаемых приемником, будет равна
частоте v
0
колебаний источника. Если же источник или приемник, либо оба они, движутся
относительно среды, то частота v, воспринимаемая приемником, может оказаться отличной от
v
0
. Это явление называется эффектом Доплера.
Для простоты предположим, что приемник и источник движутся вдоль соединяющей их
прямой. Скорость источника
ист
будем считать положительной, если источник движется по
направлению к приемнику, и отрицательной, если источник удаляется от приемника.
Аналогично скорость приемника
np
будем считать положительной, если приемник
приближается к источнику, и отрицательной, если приемник удаляется от источника.
Если источник неподвижен и колеблется с частотой v
0
, то к моменту, когда источник будет
завершать v
0
-e колебание, порожденный первым колебанием «гребень» волны успеет пройти в
среде путь
(
– скорость распространения волны относительно среды). Следовательно,
порождаемые источником за секунду v
0
«гребней» и «впадин» волны расположатся на длине
.
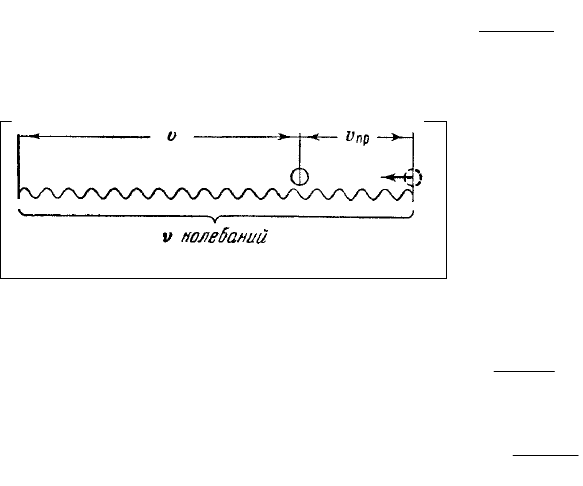
Если же источник движется относительно
среды со скоростью
ист
, то в момент, когда
источник будет завершать v
0
-e колебание,
«гребень», порожденный первым колебанием,
будет находиться от источника на расстоянии
`–
ист
(рис. 207). Следовательно, v
0
«гребней»
и «впадин» волны уложатся на длине
–
ист
,
так что длина волны будет равна
Рис. 205.
Рис 207.
13
èñò
0
(86.1)
Мимо неподвижного приемника пройдут за секунду «гребни» и «впадины»,
укладывающиеся на длине v.
Если приемник движется со скоростью
np
, то в
конце секундного промежутка времени он будет
воспринимать «впадину», которая в начале этого
промежутка отстояла от его теперешнего
положения на v. Таким образом, приемник
воспримет за секунду колебания, отвечающие
«гребням» и «впадинам», укладывающимся на длине
+
np
(рис. 208), и будет колебаться с
частотой
ï ð
(86.2)
Объединив выражения (86.2) и (86.1), получим:
ï ð
0
èñò
(86.3)
Согласно формуле (86.3) при таком движении приемника и источника, что расстояние
между ними сокращается, воспринимаемая приемником частота v оказывается больше частоты
источника v
0
. Если расстояние между источником и приемником растет, v будет меньше, чем
v
0
. Когда направление движения источника и приемника не совпадает с направлением
соединяющей их прямой, в формуле (86.3) под
ист
и
np
следует понимать проекции скоростей
источника и приемника на направление указанной прямой.
ТЕОРИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ.
Согласно идеям Максвелла переменное магнитное поле всегда связано с порождаемым им
электрическим полем, в свою очередь переменное электрическое поле всегда связано с
порождаемым им магнитным. Другими словами, они образуют единое электромагнитное поле.
То же самое можно получить, рассматривая принцип относительности, установленный для
механических явлений. В этом случае следует распространить его на все другие физические
явления. Тогда законы физических явлений, в том числе и электромагнитных, должны иметь
одинаковый вид (т.
`
е. описываться одинаковыми уравнениями) во всех инерциальных системах
отсчета.
Из принципа относительности вытекает, что раздельное рассмотрение электрического и
магнитного полей имеет лишь относительный смысл. Действительно, электростатическое поле
создается системой неподвижных зарядов. Однако, если заряды неподвижны относительно
некоторой инерциальной системы отсчета, то относительно других инерциальных систем эти
заряды движутся и, следовательно, будут порождать не только электрическое, но и магнитное
поле (движущийся заряд эквивалентен току). Неподвижный провод с постоянным током
создает в каждой точке пространства постоянное магнитное поле. Однако относительно
других инерциальных систем этот провод находится в движении. Поэтому создаваемое им
магнитное поле в любой точке с данными координатами х, у, z будет меняться и,
следовательно, порождать вихревое электрическое поле. Таким образом, поле, которое
относительно некоторой системы отсчета оказывается «чисто» электрическим или «чисто»
магнитным, относительно других систем отсчета будет представлять собой совокупность
электрического и магнитного полей.
Прежде, чем начать анализ уравнений Максвелла обратим внимание на серьезные
математические сложности, связанные с интегральным характером соотношений между
магнитным и электрическим полями:
Рис. 208.
14

l
S
n
B
E dl dS
t
,
0
n
S
B dS
( ) ( )
l ï î ëí n ï ð n
S S
H dl j dS j dD dt dS
,
n
S V
D dS dV
С позиций физики недостаток этих соотношений заключается в невозможности
определения силового или энергетического воздействия на соответствующий заряд или ток в
любой заданной точке, то есть невыполнении основного положения определения поля.
Следовательно, необходимо математически преобразовать эти уравнения к виду,
позволяющему подобное определение. Такое преобразование означает приведение уравнений
к виду дифференциальному. При интегрировании дифференциальных уравнений константы
интегрирования могут быть определены с использованием некоторых частных, известных из
условий задачи, значений поля в определенных точках и в заданный момент времени.
Описание свойств векторных полей.
Величина потока вектора через некоторую поверхность и циркуляции вектора по
заданному контуру дают среднюю характеристику поля. При этом поле определяется в
пределах объема, охватываемого поверхностью, через которую определяется поток, или в
окрестности контура, по которому берется циркуляция. Уменьшая размеры поверхности или
контура вплоть до точки, можно прийти к величинам, которые будут характеризовать
векторное поле в данной точке. Чтобы ввести эти величины, следует глубже вникнуть в смысл
понятий потока и циркуляции.
Воспользуемся уже известной аналогией между векторами электрического и магнитного
полей и векторами, характеризующими ламинарное движение жидкости. Жидкость будем
рассматривать как несжимаемую и неразрывную.
Пусть нам дано поле вектора скорости жидкости. Поток вектора скорости через некоторую
поверхность дает объем жидкости, протекающей через эту поверхность в единицу времени.
Рассмотрим в окрестности некоторой точки Р замкнутую поверхность
S (рис. 230). Если в объеме V, ограниченном поверхностью, жидкость не
возникает и не исчезает, то суммарный поток Ф
жидк
, протекающий через
поверхность, будет, очевидно, равен нулю. Отличие потока от нуля
означает, что внутри поверхности имеются точки, в которых жидкость
поступает в объем (источники), либо удаляется из объема (стоки).
Величина потока определяет суммарную алгебраическую мощность
источников и стоков. Под мощностью источника или стока понимается объем жидкости,
выделяемый или, соответственно, поглощаемый в единицу времени. Сток можно
рассматривать как источник с отрицательной мощностью.
При преобладании мощности источников над мощностью стоков величина потока будет
положительной, при преобладании мощности стоков – отрицательной.
Частное от деления потока Ф
жидк
на величину объема, из которого поток вытекает, т. е.
æèäê
/Ô V
(107.1)
назовем средней удельной мощностью источников, заключенных в объеме V. Чем меньше
объем V, включающий в себя точку Р, тем ближе это среднее к истинной удельной мощности в
этой точке. В пределе при стремлении V к нулю, т. е. при стягивании объема V к точке Р,
выражение (107.1) даст истинную удельную мощность источников в точке Р, которую
называют дивергенцией (или расхождением) вектора
(обозначается div
). Таким образом,
по определению
div lim
æ èäê
V P
Ô
V
Аналогично определяется дивергенция любого вектора
A
:
Рис. 230
15
1
div lim lim
A
n
V P V P
S
Ô
A A dS
V V
(107.2)
Интеграл берется по произвольной замкнутой поверхности S, ограничивающей объем V.
Так как
V P
, причем
0S
, выражение (107.2) от формы поверхности зависеть не может.
Понятно, что дивергенция определяется поведением векторной функции А(Р) в
окрестности данной точки, т. е. характером изменения вектора
A
(или его компонент А
х
, A
y
, A
z
)
при переходе от одной точки пространства к другой.
Поскольку интеграл в определении (107.2) берется от
нормальных к поверхности компонент, а направления нормалей
принимают все возможные направления, дивергенция есть
скалярная функция координат, определяющих положения точек
в пространстве или, для краткости, является функцией точки.
Кроме того, определение (107.2) общее, оно не зависит от
выбора координатной системы.
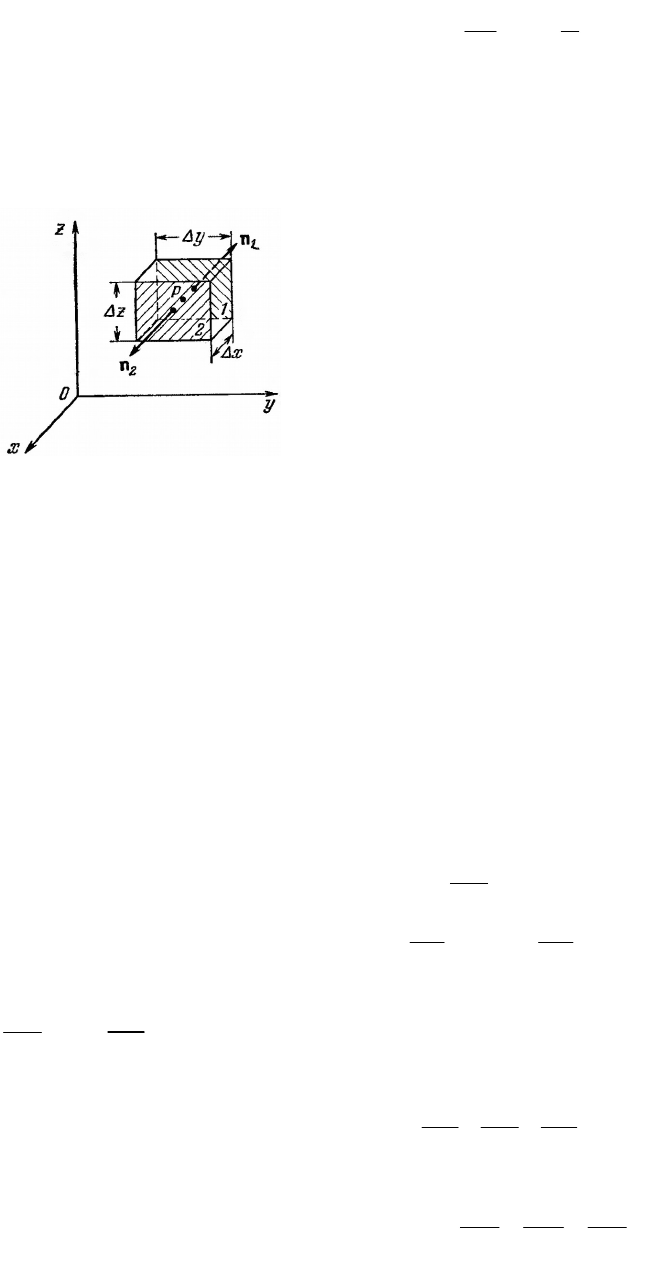
Форма поверхности, по которой берется интеграл в
выражении (107.2), произвольна. Поэтому в декартовой системе
координат в окрестности точки Р(х, у, z) выделим малый объем
в виде параллелепипеда. Ребра направим параллельно координатным осям (рис. 231). Ввиду
малости объема [согласно (107.2) мы будем его стремить к нулю] значения А
х
, А
у
, А
z
на каждой
из граней параллелепипеда можно считать постоянными. Поток через всю замкнутую
поверхность образуется из потоков, текущих через каждую из шести граней в отдельности.
Найдем поток через пару граней, перпендикулярных к оси х (на рис. 231 эти грани
заштрихованы косой штриховкой и помечены цифрами 1 и 2). Внешняя нормаль n
2
к грани 2
совпадает с направлением оси х. Следовательно, A
n2
= А
х2
и поток через грань 2 равен A
x2
yz
(индекс 2 указывает на то, что значение А
х
берется в том месте, где расположена грань 2).
Нормаль n
1
к грани 1 имеет направление, противоположное оси х. Поэтому проекции вектора
на ось х и на n
1
имеют противоположные знаки.
Суммарный поток через грани 1 и 2 равен
2 1x x
A A y z
(107.3)
Разность A
x2
– А
х1
есть приращение А при смещении вдоль оси х на х. Ввиду малости х
это приращение можно представить в виде
x
A
x
x
. Тогда (107.3) переходит в
x x
A A
x y z V
x x
Аналогично получаем потоки через другие пары граней, перпендикулярные к осям у и z:
y
A
V
y
и
z
A
V
z
. Тогда полный поток через всю замкнутую поверхность определяется
выражением
y
x
z
A
A
A A
Ô V
x y z
Разделив это выражение на V, найдем дивергенцию вектора А в точке Р(х, у, z):
div
y
x
z
A
A A
A
x y z
(107.4)
(предельный переход VP мы предвосхитили, полагая А
х
, А
у
и А
z
в пределах каждой из
граней постоянными величинами).
Зная дивергенцию вектора А в каждой точке пространства, можно вычислить поток этого
вектора через любую поверхность конечных размеров. Для этого (рис. 232) разобьем объем,
ограниченный поверхностью S, на большое число(в пределе бесконечное) малых объемчиков
Рис. 231.
16
(в пределе бесконечно малых). Согласно (107.2) поток вектора А,
вытекающий из любого из них, может быть записан в виде
ï î òî ê divA V
.
Если просуммировать это выражение по всем объемчикам, справа
получится
div
V
AdV
, взятый по всему объему, ограниченному поверхностью
S, а слева – поток вектора А через поверхность S. Дело в том, что каждый из потоков, текущих
через разделяющие грани, войдет в сумму дважды с противоположными знаками (значения А
n
для соседних объемчиков одинаковы по абсолютной величине, но отличаются знаком).
Поэтому потоки через внутренние перегородки взаимно уничтожатся. Не компенсированы
только потоки через внешние грани, которые в сумме дадут поток через поверхность S.
Таким образом:
div
n
S V
A dS AdV
(107.5)
Это соотношение носит название теоремы Остроградского-Гаусса. Она позволяет связать
поток вектора (например, вектора
E
) с его дивергенцией.
Если теперь удобным образом ввести представление о циркуляции, то переход к
дифференциальной форме уравнений Максвелла значительно облегчится.
Выделим в течении идеальной несжимаемой жидкости замкнутую линию – контур Г.
Предположим, что каким-то способом мы заморозим мгновенно жидкость во всем объеме, за
исключением очень тонкого замкнутого канала постоянного сечения, включающего в себя
контур Г (рис. 233).
В зависимости от характера течения (от характера поля вектора
скорости) жидкость в образовавшемся канале окажется либо
неподвижной, либо будет двигаться вдоль контура (циркулировать) в
одном из двух возможных направлений.
В качестве меры этого движения возьмем величину, равную
произведению скорости жидкости в канале, умноженной на длину
контура l. Эту величину назовем циркуляцией вектора
по контуру Г
(ср. с определением циркуляции векторов
E
или
H
).
Тогда,
öèðêóëÿöèÿ ï î Ã l
(поскольку канал по предположению имеет постоянное сечение, модуль скорости
есть
постоянная величина).
В момент затвердевания стенок у каждой из частиц жидкости в канале будет погашена
составляющая скорости, перпендикулярная к стенке, и останется лишь составляющая скорости
l
, касательная к контуру. С этой составляющей связан импульс dp
l
, модуль которого для
частицы жидкости, заключенной в отрезке канала длины dl, имеет величину
v
l
dl (
–
плотность жидкости,
– площадь поперечного сечения канала). Поскольку жидкость
идеальна, действие стенок может изменить лишь направление dp
l
, но не его величину.
Взаимодействие между частицами жидкости вызовет такое перераспределение импульса
между ними, которое выровняет скорости всех частиц. При этом алгебраическая сумма
импульсов не может измениться: импульс, приобретаемый одной из взаимодействующих
частиц, равен импульсу, теряемому второй частицей. Это означает, что
l
l dl
где
– скорость циркуляции,
l
– касательная составляющая скорости жидкости в объеме
dl в момент времени, предшествовавший затвердеванию стенок канала.
Сократив на
, получим, что
Рис. 232.
Рис. 233.
17

öèðêóëÿöèÿ ï î Ã
l
l dl
Аналогично определяется циркуляция любого вектора А по произвольному контуру Г:
öèðêóëÿöèÿ À ï î Ã
l l
Al A dl
(107.6)
где
l
A
– среднее по контуру значение касательной составляющей вектора А.
Можно подумать, что для отличия циркуляции от нуля векторные линии должны быть
замкнутыми или хотя бы как-то изогнутыми в направлении обхода по контуру. Легко
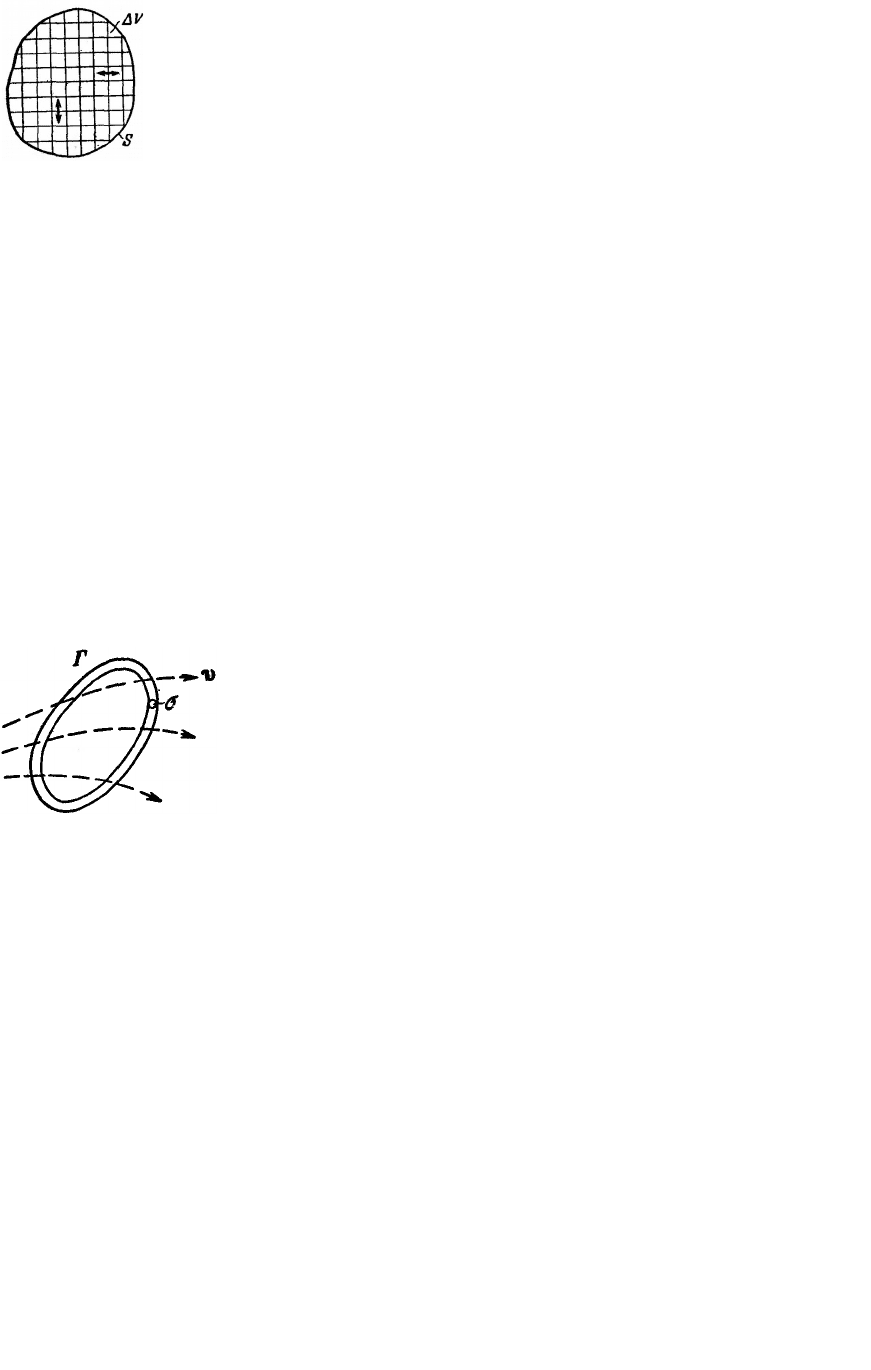
убедиться в ошибочности такого предположения. Рассмотрим ламинарное течение жидкости в
реке. Скорость жидкости непосредственно у дна равна нулю
и возрастает при приближении к поверхности воды (рис. 234).
Линии тока (линии вектора
) прямолинейны. Несмотря на
это, циркуляция вектора
по изображенному пунктиром
контуру, очевидно, отлична от нуля.
Циркуляция характеризует свойства поля, усредненные по
области с размерами порядка поперечника контура Г. Чтобы
получить характеристику свойств поля в точке Р, нужно
уменьшать размеры контура Г, стягивая его в точку Р. Однако сама циркуляция при этом
обратится в нуль. Действительно, среднее значение A
l
конечная величина, а длина контура l в
пределе равна нулю. Следовательно, и произведение
l
Al
, обращается в нуль. Поэтому
целесообразно в качестве характеристики поля вектора А в точке Р взять предел отношения
циркуляции вектора А по плоскому контуру Г, стягивающемуся к точке Р, к величине площади
контура S:
öèðêóëÿöèÿ À ï î Ã
lim
S P
S
(107.7)
Однако при нахождении предела (107.7) обнаруживается следующее осложнение: величина
этого предела зависит не только от свойств поля в точке Р, но также и от ориентации контура в
пространстве, которая может быть задана направлением положительной нормали n к
плоскости контура (положительной считается нормаль, связанная с направлением обхода
контура при интегрировании правилом правого винта). Определяя предел (107.7) в одной и той
же точке Р для разных направлений n, мы будем получать различные значения, причем для
противоположных направлений эти значения отличаются только знаком (изменение
направления n на противоположное эквивалентно изменению направления обхода по контуру
во время интегрирования, что вызовет лишь изменение знака у циркуляции).
Таким образом, величина (107.7) ведет себя как проекция некоторого вектора на
направление нормали к плоскости контура, по которому берется циркуляция. Для какого-то
направления нормали величина (107.7) в данной точке окажется максимальной.
Максимальное значение величины (107.7) определяет модуль этого вектора, а направление
положительной нормали n, при котором достигается максимум, дает направление вектора.
Этот вектор называется ротором (или вихрем) вектора А. Обозначается он символом
rot A
.
Используя это обозначение, можно записать выражение (107.7) в виде
öèðêóëÿöèÿ À ï î Ã
lim (rot )
n
S P
A
S
(107.8)
Под
(rot )
n
A
подразумевается проекция вектора
rot A
на положительную нормаль к
площадке S, охватываемой контуром Г.
Выражение (107.8) может служить определением вектора
rot A
. Из него следует, что ротор есть векторная функция точки
Р. Определение (107.8) является самым общим, не зависящим от
Рис. 234.
Рис. 235.
18

выбора системы координат. Для того чтобы найти выражения для проекций вектора
rot A
на
оси декартовой системы координат, нужно определить значения величины (107.8) для таких
ориентаций площадки S, при которых нормаль n к площадке совпадает с одной из осей х, у, z.
Если, например, направить n по оси х, то (107.8) превратится в (rotA)
x
. Контур Г
расположен в этом случае в плоскости, параллельной координатной плоскости yz. Возьмем
этот контур в виде прямоугольника со сторонами А
у
и А
z
(рис. 235; ось х имеет на этом рисунке
направление на нас; указанное на рисунке направление обхода связано с направлением оси х
правилом правого винта). Имея в виду предельный переход SP, можно считать значения А
у
и
А
z
на каждой из четырех сторон контура постоянными. Участок 1 контура противоположен по
направлению оси z. Поэтому A
l
на этом участке совпадает с–A
z1
(индекс 1 указывает на то, что
А
z
берется в том месте, где расположен участок 1). Рассуждая аналогично, найдем, что A
l
на
участках 2, 3 и 4 равна соответственно А
у2
, A
z3
и – A
y4
. В итоге получим для циркуляции
значение
(A
z3
– А
z1
) z – (A
y4
– A
y2
) у (107.9)
Разность A
z3
– А
z1
представляет собой приращение Аz при смещении вдоль оси у на у.
Ввиду малости у это приращение можно представить в виде
z
A
y
y
. Аналогично разность A
y4
– A
y2
можно представить в виде
y
A
z
z
. Подставив эти выражения в (107.9) и вынося общий
множитель за скобки, получим
öèðêóëÿöèÿ
y y
z z
A A
A A
A y z S
y z y z
где S – площадь контура. Разделив циркуляцию на S, найдем выражение для проекции
rotА на ось х:
(rot )
y
z
x
A
A
A
y z
(107.10)
(предельный переход SP мы уже учли, предположив, что на каждом из участков контура
А
у
и А
z
неизменны). Путем аналогичных рассуждений можно найти, что
(rot )
x z
y
A
A
A
z x
(107.11)
(rot )
y
x
z
A
A
A
x y
(107.12)
Легко убедиться в том, что любое из выражений (107.10) – (107.12) может быть получено
из предыдущего [для (107.10) предыдущим следует считать (107.12)] путем так называемой
циклической перестановки координат, т. е. замены координат, осуществляемой по схеме:
Итак, ротор вектора А определяется в декартовой системе координат следующим
выражением:
rot
y y
x x
z z
A A
A A
A A
A i j k
y z z x x y
(107.13)
Ниже будет приведен более изящный способ записи этого выражения.
Зная ротор вектора А в каждой точке некоторой поверхности S, можно вычислить
циркуляцию этого вектора по контуру, ограничивающему S. Для этого разобьем поверхность
19

на очень малые элементы S. Согласно (107.8) циркуляция вектора А по
контуру, ограничивающему S, может быть представлена в виде
öèðêóëÿöèÿ À ï î Ã=( )
n
rotA S
,
где n – положительная нормаль к элементу поверхности S.
Просуммировав эти выражения по всей поверхности S, справа получим
(rot )
n
S
A dS
, слева – циркуляцию А по контуру Г. Действительно, при
суммировании слагаемые A
l
l, отвечающие отрезкам, разделяющим смежные элементы
поверхности, взаимно уничтожатся.
Например, для A
S
, лежащей слева от MN (рис. 236), этот участок при определении
циркуляции проходится в направлении NM, а для A
S
, лежащей справа от MN, тот же участок
проходится в направлении MN. Следовательно, отвечающие MN слагаемые A
l
l отличаются
для смежных площадок лишь знаком и при сложении дают нуль. Некомпенсированными
останутся только слагаемые A
l
l для внешних (по отношению ко всей поверхности S) участков
отдельных контуров, которые в сумме дадут
l
A dl
. Таким образом, мы пришли к
соотношению
( )
l n
S
A dl rotA dS
(107.14)
которое носит название теоремы Стокса.
Написание формул векторного анализа значительно упрощается и облегчается, если ввести
в рассмотрение векторный дифференциальный оператор, обозначаемый символом (набла) и
носящий название оператора набла или оператора Гамильтона. Под этим оператором
подразумевается вектор с составляющими /x, /y, и /z:
( ) ( ) ( )i x j y k z
(107.15)
Сам по себе этот вектор смысла не имеет. Он приобретает смысл в сочетании со скалярной
или векторной функцией, на которую он символически умножается. Так, если умножить
вектор на скаляр
, то получится вектор градиента функции
i j k grad
x y z
(107.16)
Если вектор умножить скалярно на вектор А, получится скаляр – дивергенция вектора А
[см. (107.4)].
y
x
z
x x y y z z
A
A
A
A A A A A divA
x y z
(107.17)
Наконец, если умножить на А векторно, получится вектор с составляющими:
( )
x y z z y z y
A A A A y A z
и т. д., которые совпадают с составляющими rotА [см. (107.10) – (107.12)].
Воспользовавшись записью векторного произведения с помощью определителя, можно
написать:
x y z
i j k
rotA A
x y z
A A A
(107.18)
Пользуясь вектором , нужно помнить, что он является дифференциальным оператором,
действующим на все функции, стоящие справа от него. Поэтому при преобразовании
выражений, в которые входит , нужно учитывать как правила векторной алгебры, так и
правила дифференциального исчисления. Так, например, производная произведения функций
и
равна
Рис. 236.
20
