Островський А.Л., Мороз О.І., Тарнавський В.Л. Геодезія, частина II

Подождите немного. Документ загружается.

новлюватись в будь-якій з цих точок. Нам потрібно вивести формули для

двох випадків (пряма та обернена засічка), а також загальну формулу. Ско-

ристаємося відомою формулою, аналогічною формулі (II.5.13):

Продиферснціюємо цю формулу, вважаючи, що змінними є коор-

динати тільки точки В (випадок І):

1 сіа° _(Х.-Х

)-<ІУ

~{у

-у

)-ах

соз

а р" (Х

-У

Оскільки: Х

-Х

=8са&а; У

-У

=8з,та, то враховуючи це,

формулу (ІІ.5.21) запишемо так:

1 сіа" 8соза<1¥

-85тасіХ

со з

а р" 8

ьо%

Помноживши рівняння (ІІ.5.22) на сов

а, матимемо для сіа":

(II.5.22)

, . „ С080Г „8іпа , ,„„..

сіа" = р"——Мв ~Р —^Г^в

•

(ІІ.5.23)

о і

Введемо позначення:

(д) = -/?*8Іпа1

(Ь)

= р соза ]

З врахуванням цих позначень формула (ІІ.5.23) набере кінцевого

вигляду:

<іа =

^-сІХ

+^сіУ

. (II.5.25)

8 8

Для другого випадку, коли змінюються координати точки А, то якщо

розглядати формулу (ІІ.5.20), не важко зауважити, що координати точки А в

цій формулі відрізняються від координат точки В знаками. Тому для другого

випадку кінцеву формулу можна записати за аналогією з формулою (II.5.25):

= (ІІ.5.26)

Відповідно, для загального випадку, матимемо формулу:

йа=М

Лл

Мах

М<ІУ

. (И.5.27)

8 8 8 8

Як бачимо з цих формул, щоб знайти малі зміни дирекційних кутів

сіа, необхідно крім зміни координат точок, ще знати довжини ліній 8

та

коефіцієнти (а),, і (Ь\.

11.5.6. Обернена багаторазова кутова засічка

Суть оберненої багаторазової кутової засічки пояснена в підрозділі

ІІ.5.4. Для складання рівнянь, на основі яких можна буде знайти поправки

та 5

в наближені координати точки, скористаємось рисунком II.5.6, на

якому зображені дві вихідні ("тверді") точки Т

та Т

; точка Р

, наближені

координати якої X

та У

, та точка Р, найімовірніші координати якої X та У

поки що невідомі.

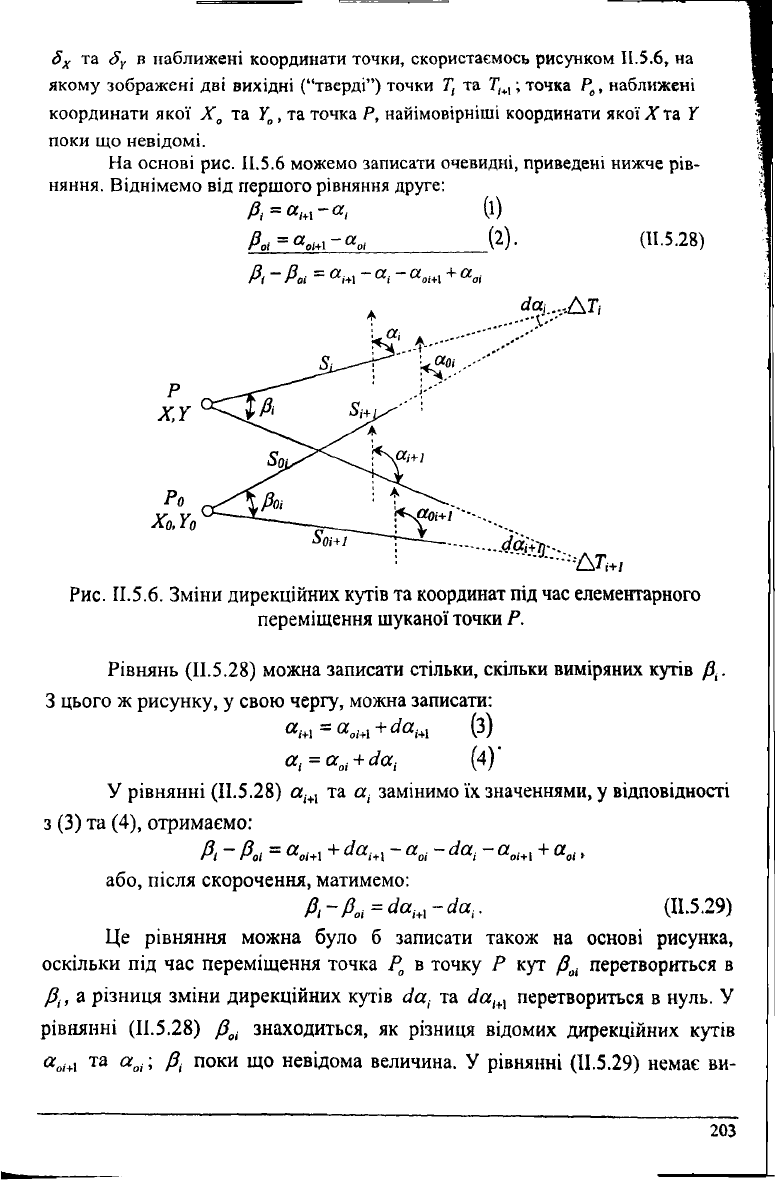
На основі рис. II.5.6 можемо записати очевидні, приведені нижче рів-

няння. Віднімемо від першого рівняння друге:

)

Роі=<*О

-<*« (2)- (11.5.28)

Рис. ІІ.5.6. Зміни дирекційних кутів та координат під час елементарного

переміщення шуканої точки Р.

Рівнянь (II.5.28) можна записати стільки, скільки виміряних кутів Д.

З цього ж рисунку, у свою чергу, можна записати:

м=

ом

+<іа

м (з)

= а

+ сіа

(4)'

У рівнянні (ІІ.5.28) а

та а

замінимо їх значеннями, у відповідності

з (3) та (4), отримаємо:

Д ~

Рої

ом + ~ - ~

ом + «о, .

або, після скорочення, матимемо:

= (ІІ.5.29)

Це рівняння можна було б записати також на основі рисунка,

оскільки під час переміщення точка Р

в точку Р кут /3

0і

перетвориться в

Д, а різниця зміни дирекційних кутів с!а

;

та <іа

перетвориться в нуль. У

рівнянні (ІІ.5.28) Д

знаходиться, як різниця відомих дирекційних кутів

ом

та а

оі; Д

поки

невідома величина. У рівнянні (11.5.29) немає ви-

203

міряного кута. Позначимо виміряний кут Д' і введемо його в рівняння

(II.5.29), віднявши і додавши його. Отримаємо:

д -Д'+Д'-Д,

аа

-а

,. (іі.5.зо)

Позначимо відому різницю

Д„,

Д'

= . а невідому різницю

Д - Д' = V,., тоді (ІІ.5.30) набуде вигляду рівняння похибок:

у, =Л*,

-</«,+/,. (ІІ.5.31)

Замінимо в формулі (ГІ.5.31) зміни дирекційних кутів сІа

та сіа.

змінами координат у відповідності з отриманою диференційною формулою

(II.5.26), (обернена засічка): під час зміни координат точки Р

, змінюються

дирекційні кути а

вМ

та а

оі

у<=

сі

№СІУ-^СІХ-&Асі¥ + І

, (ІІ.5.32)

ОУ+1

або

V,- = •

еі+І

ОІ+1

СІУ +

І.

Позначимо

4 =

(II.5.33)

(II.5.34)

і ОІ °о/+1)

і.

°в/ °оі+і ^

Тоді отримаємо скорочений, кінцевий вигляд рівнянь похибок:

= + + (II.5.35)

Таких рівнянь можна записати стільки, скільки виміряних кутів:

V, =

сіх+В

сіу+1

= А

сІх+В

сіу+І

у^Ауск+В^у +

І!

(ІІ.5.36)

Нормальних рівнянь буде стільки, скільки невідомих. У нас невідомі

сіх та ф/. Тому буде два рівняння:

\АА\ІХ

[АВ\ІУ + [АЇ\ = 01

{АВ\іх+[ВВ\іу+[Ві}=о)'

Знайдемо невідомі сіх та сіу.

(ІІ.5.37)

[АВ)[ВІ

~[вв

\ЛІ]

[АА\ВВ

[АВ][АІ

-[АВ

-\АА

АВ]

[ВІ]

[АА][ВВІ

-[АВ

АВ)

(ІІ.5.38)

204

Оскільки 5, в км, а р" приймемо рівним 20,6265, тоді аЬс та сіу буде

виражено в десятих долях метра (в дециметрах). Тому:

Х = Х

+ 0,1

У = Г

+0,\ф

(11.5.39)

11.5.7. Точність прямої та оберненої багаторазових кутових засічок

Для оцінки точності таких засічок необхідно визначити середні

квадратичні похибки вимірювання кутів т

та середні квадратичні похибки

та т

визначення координат точки Р. Як відомо, з теорії похибок, т^

визначається за формулою:

(ІІ.5.40)

л-2

Похибки V, = Д - Д' (Д - виправлені, Д' - виміряні кути) знайдуть-

ся за системою рівнянь похибок (ІІ.5.36). У знаменнику формули (ІІ.5.40),

(п-2) - кількість надлишкових виміряних кутів (два необхідних). Квадра-

тичні похибки т

та т

визначаться за формулами:

т. - —-

ГПр

(И.5.41)

де Р

та Р - ваги вимірів.

Як відомо, Р = [вві]=[вв}-1ф^.

[АА\

У =

(II.5.42)

або

[АА][ВВ)-[АВ\АВ]

[лл]

Як бачимо, чисельник формули (II.5.42) дорівнює знаменникам

системи рівнянь (II.5.38). Позначимо:

О = [АА\ВВ]-[ав][АВ\. (Н.5.43)

Тоді формула ваги Р

скорочено запишеться так:

(4.5.44)

й - вже відома величина і її не потрібно вираховувати, як і суму [лл]. У

свою чергу, вага Р

знаходиться за формулою:

„ ІАА

ВВ

(11.5.45)

З врахуванням (II.5.44) для Р

маємо:

205

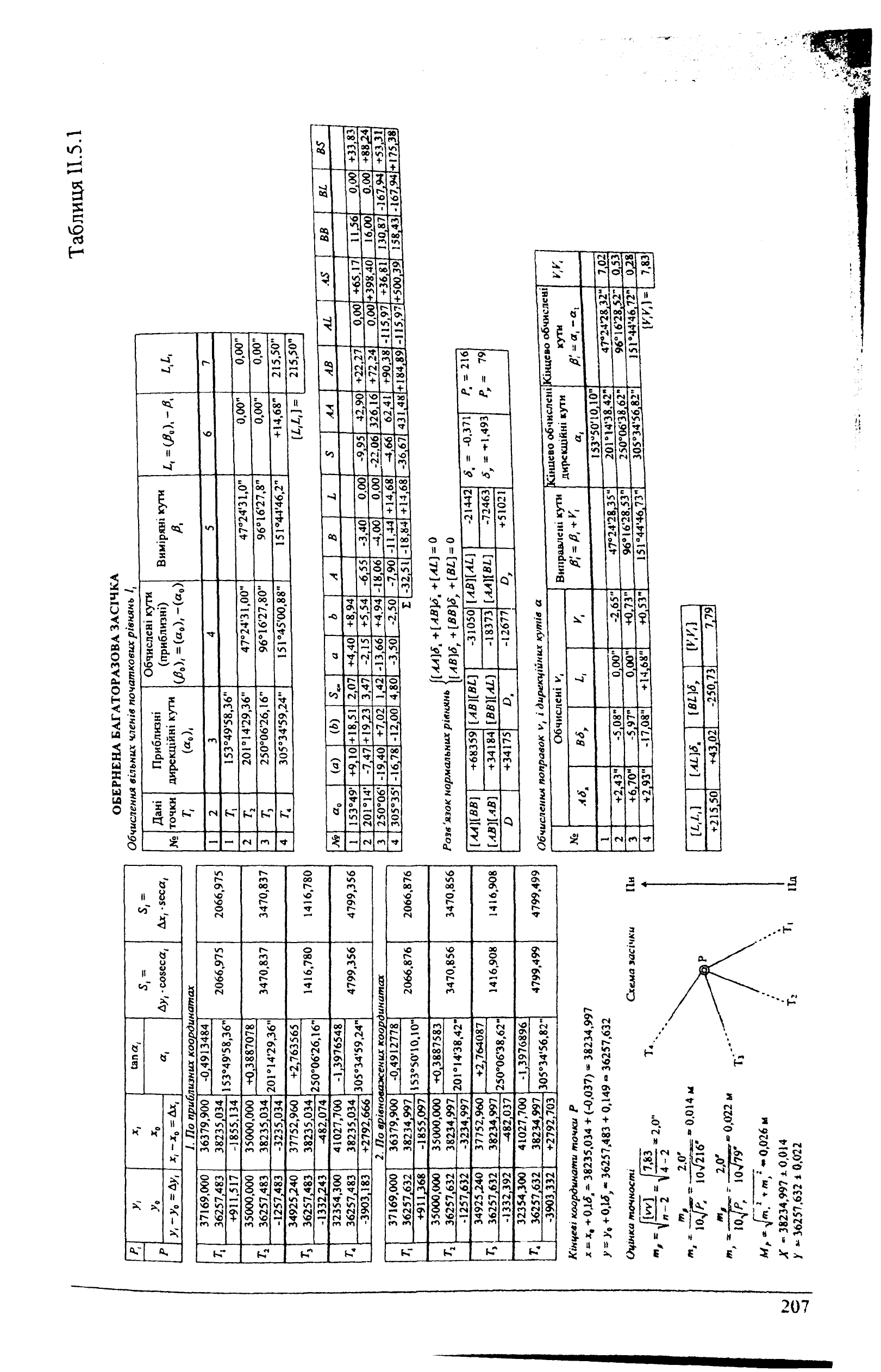
У таблиці 11.5.1 подано приклад розв'язку оберненої багаторазової

засічки з оцінкою

точності

обчислення найімовірніших координат.

11.5.8. Точність прямої та оберненої одноразових кутових засічок

Для кожної з таких засічок вимірюється два кути: для прямої -

одному куту на двох точках, а для оберненої - два кути на одній точці (див.

рис. 11.5.1).

Рис. ІІ.5.7. Визначення точності одноразових засічок: 1) прямої, 2)

оберненої.

Для таких засічок можна скласти тільки по два рівняння похибок

виду (ІІ.5.35).

У відповідності з формулами (ІІ.5.41) можемо записати формулу

похибки в визначенні координат точки Р:

= т

+ т

або

Підставляючи в (ІІ.5.47) значення обернених ваг будемо мати після

деяких перетворень:

(11.5.48)

Р 8ІП у

Якщо 5, = 5

= 5, а у = 90°, тоді формула (И.5.48) прийме вигляд:

(11.5.49)

іП

\о

н К

__ (Л

II Й

«О 3

«Г

ЇЇ

Ц-

* £

О.

207

Як бачимо, похибка координат точки Р прямо пропорційна довжині

ліній та похибці вимірювання кутів. Якщо т"

= 5", = 3000 м, тоді

=0,10 м. Для оберненої одноразової засічки оцінити точність визна-

чення координат значно складніше. Професором Чеботарьовим О.С. запро-

понований наступний метод [28]. Будується так званий "зворотний"

трикутник (рис. ІІ.5.7). Для цього обчислюється величина

(II.5.50)

Значення г

(

відкладають по напрямках від точки Р. Отримують на

лініях 5,, точки 1, 2, 3, що є вершинами "зворотного" трикутника.

Довжини сторін цього трикутника сг,, а

, сг

вимірюються графічно.

Вираховують площу трикутника Р також графічно, або за формулою Герона.

Похибка М

в положенні точки Р визначається за формулою:

+СГ

+С7

). т

напр

де:

Кап

- —

•Я'

(ІІ.5.51)

(ІІ.5.52)

- похибка вимірювання кутів, т - похибка вимірювання напрямків.

11.5.9. Лінійна геодезична засічка

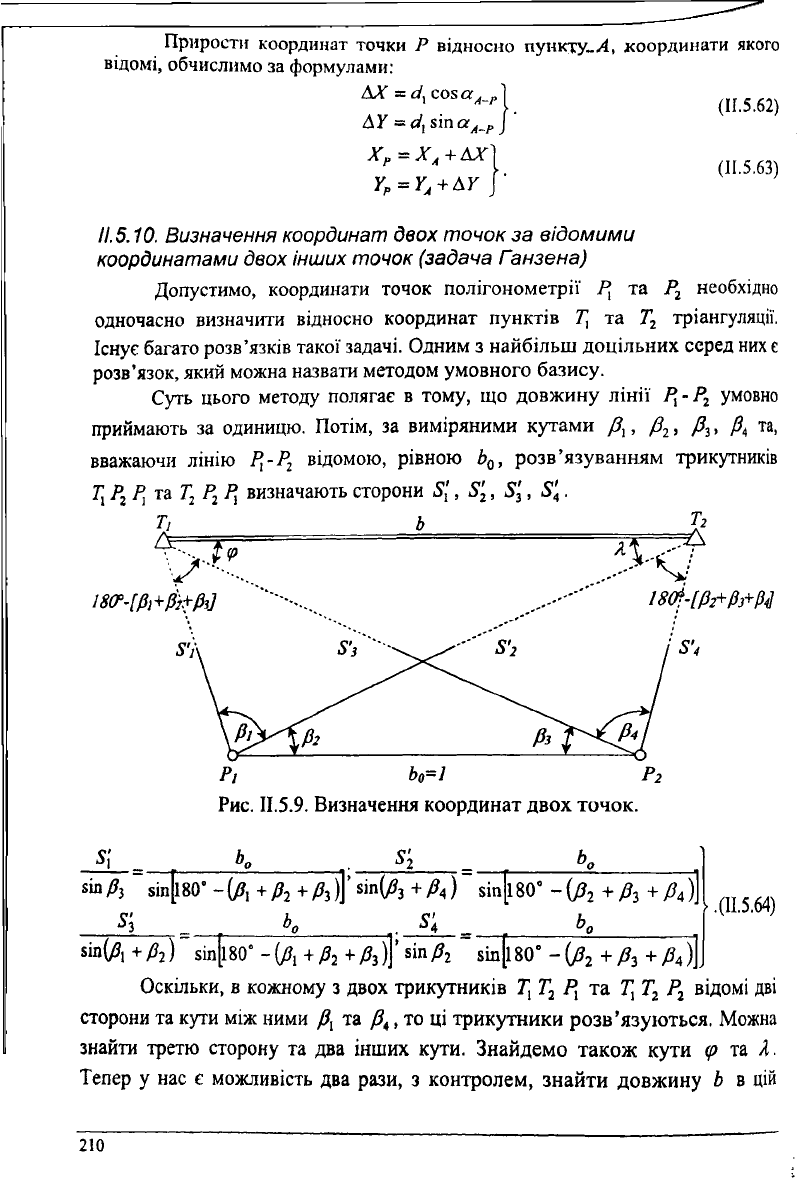
Визначення координат точки Р

за координатами двох вихідних (відо-

мих) пунктів А і В та двома виміряними

віддалями <і

та <1

від шуканої точки

до вихідних пунктів називають ліній-

ною геодезичною засічкою.

Розв'язавши обернену геодезич-

ну задачу, за координатами точок

А(Х

,¥

) та В(Х

,У

), визначимо

довжину сторони АВ=сІ, та її дирек-

ційний кут а

. Тоді в трикутнику

АВР будуть відомі усі три сторони.

Трикутник розв'язується.

За формулами тригонометричних функцій косинусів (або тангенсів)

половинних кутів обчислимо кути трикутника:

Рис. ІІ.5.8. Лінійна геодезична

засічка.

С08

£= \«Р-*г).

2 \ «Ц

(II.5.53)

208

С08—=

2 \

С08—=

2 ^

^=^ • (II.5.54)

<*А

^^ • (II.5.55)

де р

—

+ +

~ півпериметр трикутника АВР.

Знаючи всі шість елементів трикутника АВР, за формулами прямої та

оберененої засічок можна обчислити координати точки Р два рази: за

координатами точки А та координатами точки В. Контролюють обчислення

за співпадінням координат. Проте, якщо зроблено похибку підчас польового

вимірювання лінії сі

або Л

, то ця похибка не виявиться. Тому, для кон-

тролю польових вимірювань, потрібно мати не дві, а три вихідних точки та

виміряти ще одну, третю лінію.

Розв'язок може бути виконаний і без обчислення кутів трикутника

АВР [8]. Покажемо це. Знайдемо основу перпендикуляра точки Р на лінії АВ.

Залежно від того, тупий чи гострий кут /?, отримаємо основу перпенди-

куляра (точку О) на продовженні лінії ВА, або на лінії АВ.

Відрізок ^ - проекція сІ

на сІ\ ц -

сІ

со8 р. Кут р поки-що неві-

домий.

Якщо кут Р гострий, матимемо:

(і

= сі

+ с/,

-2сІц. (11.5.56)

Якщо кут Р тупий, то:

сі? =с!

+ <ії-гсІ

. (ІІ.5.57)

В нашому випадку Р гострий кут. Тому маємо:

ЛЧС/,

2 А

З прямокутного трикутника АРИ можемо записати:

к = =«/,

іп/?. (ІІ.5.59)

Оскільки Н -

СІ

8ІП Р , то

Р = агсзіп—. (Н.5.60)

Дирекційний кут а

буде дорівнювати:

= а

±р. (И.5.61)

Знак кута /? вибирається залежно від того, ліворуч чи праворуч роз-

ташована точка Р відносно лінії АВ. Праворуч "+ Р ", ліворуч "- /?". В на-

шому випадку - ліворуч.

209

Прирости координат точки Р відносно пункту»Я, координати якого

відомі, обчислимо за формулами:

АХ =

сі

соз а

ДУ =

с!

5Іп

=Х

+АХ

У^У.+АУ

(П.5.62)

(11.5.63)

11.5.10. Визначення координат двох точок за відомими

координатами двох інших точок (задача Ганзена)

Допустимо, координати точок полігонометрії Р

та Р

необхідно

одночасно визначити відносно координат пунктів Т

та Т

тріангуляції.

Існує багато розв'язків такої задачі. Одним з найбільш доцільних серед них є

розв'язок, який можна назвати методом умовного базису.

Суть цього методу полягає в тому, іцо довжину лінії Р

-Р

умовно

приймають за одиницю. Потім, за виміряними кутами Д, Д

, Д, Д та,

вважаючи лінію Р

-Р

відомою, рівною Ь

, розв'язуванням трикутників

та Т

визначають сторони 5,', 5'

, 5

', .

Т, Ь Ь

у*

Р, Ь

=1 Р

Рис. ІІ.5.9. Визначення координат двох точок.

о _

«Мз зіп[І80°-(Д +Р

+ Д)]' 8ІП(Дз + Д

) 8ІП[і80° -(Д

+ Д

)]

.(Ц.5.64)

5ІП(Д, + Д

) $іп[І80° - (Ді +

А)]'

5ІП

А 5ш[і80° -<ф

+Д

)[

Оскільки, в кожному з двох трикутників 7] Т

та Т

відомі дві

сторони та кути між ними Д та Д

, то ці трикутники розв'язуються, Можна

знайти третю сторону та два інших кути. Знайдемо також кути ер та Я.

Тепер у нас є можливість два рази, з контролем, знайти довжину Ь в цій

210

умовній одиниці довжин. Позначимо цю умовну довжину Ь'. З трикутників

{

Р[ та Г, 7*

, відповідно маємо:

Ь' _ 5[

Ь'

.-А

ЗІпД 8ІпЯ зіп зіп

(р

(II.5.65)

Отже, дійсно Ь' визначено з контролем (два рази). Два результати Ь'

повинні сходитися в межах точності обчислень. Але фактичну довжину цієї

лінії Ь та її дирекційний кут ми можемо визначити за координатами пунктів

{

та Т

З відношення Ь до Ь' ми знайдемо дійсну довжину лінії Р,-Р

Позначимо цю довжину 5 :

5 =

Ь'

(ІІ.5.66)

Тепер у нас є всі необхідні дані, щоб знайти дирекційні кути і фак-

тичну довжину всіх чотирьох ліній:

її; ~ 82' 8 \

•

5 \ 5^

5 .

Залишається за довжинами ліній та дирекційними кутами визначити

прирости координат, а потім і координати точок Р

{

та Р

. Координати кож-

ної з цих точок будуть обчислені два рази, що і буде їх кінцевим контролем.

Розглянутий спосіб є дуже простим та природнім. Найвигіднішим

випадком визначення координат двох точок буде той, коли форма, створена

двома даними та двома шуканими точками, близька до квадрату. Потрібно

уникати дуже гострих кутів у чотирикутнику.

11.5.11. Прив'язування пунктів полігонометрії до постійних об'єктів

місцевості. Відшукування полігонометричних пунктів

Від прокладення полігоно-

метричної мережі до її викорис-

тання для топознімання може

пройти декілька років, і, якби фун-

даментально не закріплювались

пункти, все ж знайти їх на міс-

цевості буває дуже важко. Головна

мета прив'язування пунктів до р р.

+і

р^

постійних предметів, як вже від-

значалося, забезпечити їх знаход-

Рис

5Л0

- Прив'язування до фасаду

ження. Способи такого прив'я- оудинку.

зування різноманітні. Суть їх стане зрозуміла після ознайомлення з типо-

вими прикладами прив'язування.

Прив'язування до фасадів будинків

Якщо полігонометричний хід проходить біля постійних предметів,

тоді прив'язування виконують переважно лінійними вимірюваннями - ру-

летками. Наприклад, якщо маємо ІМИ5- цегляну або кам'яну споруду (бу-

211