Орлова И.В. Экономико-математические методы и модели. Выполнение расчетов в среде EXCEL. Практикум
Подождите немного. Документ загружается.


Решение.
Представим данную систему в виде матричного уравнения:
'3 -1 0
УхЛ Г И
2 1
U 2
*2
-5
Е2
я {=МОБР(А2С4)}
2
1
1
2
-019231 0115385
0.346154
0115385 -0.26923
0192308
Рис. 1.2.3. Шаг
1
Вычислим матрицу, обратную для матрицы А
I {=МУМНОЖ(Е2 G4.I214)}
D
G
К
0.269
0.038
0.115
-0.19 0.115
0.346
0.115 -0.27 0.192
1
-5
8
•
Рис.
1.2.4.
Шаг 2 Найдем
неизвестн>ю
матрицу X -
Л '-В
Откуда получаем решение
системы:Х\
= \,Хг =
2,Хг
=
Ъ.
1.3. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
МЕТОДОМ ЖОРДАНА-ГА УССА
Рассмотрим систему т линейных уравнений с п неизвестными:
й\\Х\
+ai2*2
+ ...
+а\
п
х
п
~Ь\,
а
п*\
+ацХ2
+
•••
+a
ln
x
n
=b
2
,
(1.3.1)
а
т
\х
х
+а,„2Х
2
+ ...
+a
nw
x
n
=b
m
.
20

Решением системы линейных уравнений называется совокупность п
чисел
а
ь
а
2
,
...,
а„,
таких, что при подстановке их вместо неизвестных
каждое уравнение обращается в тождество.
Система линейных уравнений называется совместной, если сущест-
вует хотя бы одно ее решение. Система, не имеющая ни одного решения,
называется несовместной.
Совместные системы подразделяются на определенные, имеющие
единственное решение, и неопределенные, имеющие бесконечное мно-
жество решений.
Каждой системе линейных уравнений поставим в соответствие мат-
рицу А из коэффициентов и расширенную матрицу
А,
полученную при-
соединением к
матрицей
столбца свободных членов:
А
=
а
2\
\
а
пА
а
\2
a-ii
а
пй
а
\п
а
1п
А
=
а
\\
а
г\
а
\2
а
п
а
пА
а
пй
..
а
[п
..
а
1п
"
пт
м
ь
Ь„и
Вопрос о совместности системы линейных уравнений решается
теоремой Кронекера-Капелли: система линейных уравнений совместна
тогда и только тогда, когда ранг расширенной матрицы
А
равен рангу
матрицы А, т.е. когда
г(А) = г
(А).
На основании теоремы Кронекера-Капелли имеем:
1.
Если
г(
А)
Ф г
(А),
то система несовместна.
2.
Если
г(
А)
=
г
(А),
то система совместна.
В этом случае
г
уравнений системы линейно независимы, осталь-
ные т -
г
уравнений являются их линейной комбинацией. Поэтому в
системе оставляем лишь
г
уравнений, коэффициенты при неизвестных
которых составляют базисный минор.
В результате получим
г
линейных уравнений с
г
неизвестными.
Если
г
= п, то система имеет единственное решение.
Если
г
< и, то система имеет бесконечное множество решений, т.е.
является неопределенной. Число свободных переменных равно
п-г.
Метод
ЖорданаТаусса
применяется для решения системы т ли-
нейных уравнений с п неизвестными вида:
Х
а
у*у
=Ь
Г
т.
21

Над строками расширенной матрицы
А
осуществляем следующие
преобразования:
• перестановка любых двух уравнений;
• умножение обеих частей одного из уравнений на любое отлич-
ное от нуля число;
• прибавление к обеим частям одного уравнения соответствую-
щих частей другого, умноженных на любое число, отличное от нуля;
• вычеркивание нулевой строки (уравнения с нулевыми коэффи-
циентами и свободным членом, равным 0).
Можно показать, что элементарные преобразования переводят дан-
ную систему уравнений в эквивалентную систему. Две системы линей-
ных уравнений называются эквивалентными, или равносильными, если
каждое решение первой системы (если они существуют) является реше-
нием второй, и наоборот. Соответствующие расширенные матрицы так-
же называются эквивалентными.
При практическом решении системы линейных уравнений методом
Жордана-Гаусса последовательно над строками матрицы А выполняют
элементарные преобразования, так что некоторое неизвестное исключа-
ется из всех уравнений, кроме одного, т.е. в составе расширенной мат-
рицы формируется единичная матрица.
В процессе решения могут встретиться следующие случаи.
1.
Будет получена матрица
А,
эквивалентная матрице А, в левой
части некоторой строки ее стоят нули, а в правой — число, отличное от
нуля, что соответствует уравнению:
О •
Х
х
+ 0
•
Х
г
+
... + 0
•
Х
п
=
Ь,
ф,*0).
Это признак несовместности системы (1.3.1), т.е. система не имеет
решений.
2.
В результате преобразований получилась матрица вида:
А
=
<\ 0 ... 0
0 1 ... 0
0 0 ... 1
22

В этом случае система (1.3.1)
-
совместная, определенная
и
имеет
единственное решение:
Х\
=
Ь\,
Х
2
=
Ь
2
,
...,
Х„
=
b
h
.
3.
На
некотором этапе получилась расширенная матрица вида
О
а,'
;+1
...
а[„ Ц >
0
a^+i
...
a'
ln
bi
1
а'
п+
\
...
а'
1П
о,
t
Система совместна
и
имеет бесчисленное множество решений.
Общее решение системы можно записать
в
виде:
х\
=
Ъ{
-a[
r+
\
x
r+
\
- ...
-а[„х„,
х
2
=b{ -a2
r+
ix
r+
i
- ...
-а'
2п
х
п
,
x
r
—
b
r
a
rr
+\
х
1+
\
...
а
гп
х
п
.
Придавая каждой
из
стоящих
в
правых частях равенств переменных
Xr+i,
Х
г+
2,
...,
Х„
произвольные значения, будем получать частные реше-
ния системы.
Неизвестные
Х\, Х
2
,
...,
X,
называются базисными,
или
основными,
они соответствуют линейно-независимым
векторам^,
...,А
Г
.
Таким образом, любые
г
переменных называются базисными
(ос-
новными), если определитель матрицы коэффициентов
при них
отличен
от нуля,
а
остальные
(и -
г)
переменных называются свободными,
или
неосновными. Базисным решением системы уравнений называется част-
ное решение,
в
котором неосновные переменные имеют нулевые значе-
ния. Каждому разбиению
на
основные
и
неосновные переменные соот-
ветствует одно базисное решение,
а
количество способов разбиения
не
превышает величины
/и!
(и
—
/и)!
Если
все
компоненты базисного решения неотрицательны,
то
такое
решение называется опорным.
23
А =
f
\
О
О
1
[О
О

Пример 1.3.1. Решить методом Жордана-Гаусса систему линейных
уравнений:
Xi+X
2
+
2X
3
=
-l,
2Х\-Х
2
+
2Хт,
=
-4,
АХ
х
+Х
2
+
АХ
ъ
=
-2.
Решение.
Составим расширенную матрицу
л
(0)
=
(1
1
2 -1
И
1
2
2
4
-О
-4
-2
/
Итерация.
В качестве направляющего элемента выбираем элемент
а\^
-
1.
Пре-
образуем первый столбец в единичный. Для этого ко второй и третьей стро-
кам прибавляем первую строку, соответственно умноженную на -
2
и - 4.
Получим матрицу:
«0>
1
(
1
О -3 -2
v
0 -3-4
-О
•2
2
Итерация.
Выбираем направляющий элемент
а^
=
-3.
Так как
а\{
* 1
, то де-
лим вторую строку на
-3.
Затем умножаем вторую строку на
1
и 3 и скла-
дываем соответственно с первой
и
третьей строками. Получим матрицу:
7(2) _
1
0
0
0
1
0
4/3
2/3
-2
-5/3
N
2/3
4 ,
2.
Так как
a\J
*
1,
то
3
Итерация
Выбираем направляющий элемент
а^
делим третью строку на -2. Преобразуем третий столбец в единичный
Для этого умножаем третью строку на - 4/3 и -2/3 и складываем соот-
ветственно с первой и второй строками. Получим матрицу:
24

Г l
7(3) _
1
0
0
0
1
0
0
0
1
откуда
Xi
=
\,X
2
=
2,X^--2.
Пример 1.3.2. Решить методом Жордана-Гаусса систему линейных
уравнений:
Х
Х
-Х
2
+
Х
Ъ
-Х
А
=
А,
Jti +
A"
2
+
2ДГз
+
3Ar
4
= 8,
2ЛГ,
+
АХ
2
+
5Х
г
+
1QA4
= 20,
2ЛГ,
-4А'
2
+
Х
3
-6Х,
= 4.
Решение.
Расширенная матрица имеет вид:
л<°> =
1 -1
1 1
2 4
2 -4
-1
3
10
-6
4^
8
20
4
Применяя элементарные преобразования, получим:
f(D-
1 -1
0 2
0 6
0 -2
-1
4
12
-4
4
1
4
12
-4,
7(2)
-3
2
О
О
о
о
4
0
О
0^
4
О
О
Исходная система эквивалентна следующей системе уравнений:
Хх-ЪХг
-
Х
А
=
0,
2^
+ ^ +
4^4
=
4.
Общее решение
имеет вид:
Л
|
= Зл?
+
5А4 ,
Х
ъ
=
А-2Х
г
-
4Х
4
.
25

Найдем базисные решения. Для этого полагаем
Хг
=
О,
Х
4
- 0, тогда
X]
= 0,
Хт,
=
4.
Базисное решение имеет вид: (0,
0,4,
0).
Получим другое базисное решение. Для этого в качестве свободных
неизвестных примем
Хт,
и
*
4
.
Выразим неизвестные
Х\
и
Х
2
через неиз-
вестные
*
3
и
Х
4
:
Х\ = 6
—
1.5*2
—
-*4>
*
2
=
2-0.5*з-2*
4
.
Тогда базисное решение примет вид: (6, 2, 0, 0).
Пример 1.3.3. Решить методом Жордана-Гаусса систему линейных
уравнений:
*, +
2Х
2
+
2*, +
22*
4
-
4*
5
=
11,
X,
+
2Х
2
+Х
3
+ 16*4-4*5
= 9,
*,+*
2
+*з
+
12Х
4
-2*5
= 6.
Решение.
Составим расширенную матрицу
л
(0)
=
2
2
1
22 -4
lO
16 -4 9
12 -2 6
1 Итерация
В качестве направляющего элемента выбираем элемент
а\\'
=
1.
Пре-
образуем первый столбец в единичный. Для этого ко второй
и
третьей стро-
кам прибавляем первую строку, умноженную на
-1.
Получим матрицу:
ГО).
' 1
0
,
о
2
0
-1
2
-1
-1
22
-6
-10
-4
0
2
11
^
-2
-5 ,
2
Итерация
Выбираем направляющий элемент
aj
2
=-l.
Умножаем третью
строк>
на -1. Преобразуем второй столбец в единичный. Для этого к
26

первой строке прибавляем третью строку, умноженную на -2. Получим
матрицу:
f
\ 0 0 2 О
О
О 0-1-6 0-2
^
0 1 -1 -10 2 -5
2(2)
3
Итерация
Выбираем направляющий элемент
а[
2
--1. Так как
а$Ф\,
то
умножаем вторую строку на
-1.
Преобразуем третий столбец в единич-
ный. Для этого вторую строку складываем с третьей. Получим матрицу:
А^
=
' 1
0
0 0 2 0 1
0
16
0 2
1 0
4-23
Исходная система эквивалентна следующей системе уравнений:
Лл
+2*4=1,
Xi +
6Х
4
= 2,
Х
2
+
4Х
4
-
2Х
5
= 3.
Общее решение
имеет вид:
Xi =
1-2Д4,
Х
г
= 3
-
4Х
4
+
2Х
5
,
Х
3
=
2-
6Х
4
.
Переменные
Х
и
Х
2
,
Хт,
являются основными (или базисными). Лю-
бое
частное
решение получается из общего путем придания конкретных
значений свободным переменным. Если свободные переменные
Х
4
и
А'
5
положить равными нулю, то получим первое
базисное
решение
Х\
= 1,
Л
Г
2
=
3,А
,
1
=
2,Л
4
=
0,Я'
5
= 0.
Первое базисное решение имеет вид: (1, 3, 2, 0, 0).
27

Общее число групп основных переменных, т.е. базисных решений,
и! _ 5!
_1-2
3 4 5
да!(и-/и)!~3!(5-3)!~1-2 3 1 2
к гЧ
и! 5!
1-2
3 4 5
не более чем
Cj
=
—
=
т———
=
.
=10.
Решение примера 1.3.3 в EXCEL
В среде EXCEL общее число групп можно определить с помощью
функции ЧИСЛКОМБ.
ЧИСЛКОМБ
Возвращает количество комбинаций для заданного числа объектов.
Функция ЧИСЛКОМБ используется для определения числа всех воз-
можных сочетаний объектов в группы.
Синтаксис
ЧИСЛКОМБ (число; число_выбранных)
Число - это число объектов.
Число_выбранных
- это число объектов в каждой комбинации.
Замечания
• Числовые аргументы усекаются до целых.
• Если любой из аргументов не число, то ЧИСЛКОМБ возвращает
значение ошибки #ИМЯ?.
• Если число < 0 или число_выбранных < 0, или число < чис-
ло_выбранных, то функция ЧИСЛКОМБ возвращает значение
ошибки #ЧИСЛО!.
• Комбинацией считается любое множество или подмножество
объектов, безотносительно к их порядку. Комбинации отличают-
ся от перестановок, для которых порядок существенен.
• Число комбинаций определяется следующим образом, где число
равно п и число_выбранных равно
к:
^ Рк,п
П\
где
п
[к)
к\
к\{п-к)\'
Рк,п=-
(п-к)\
28
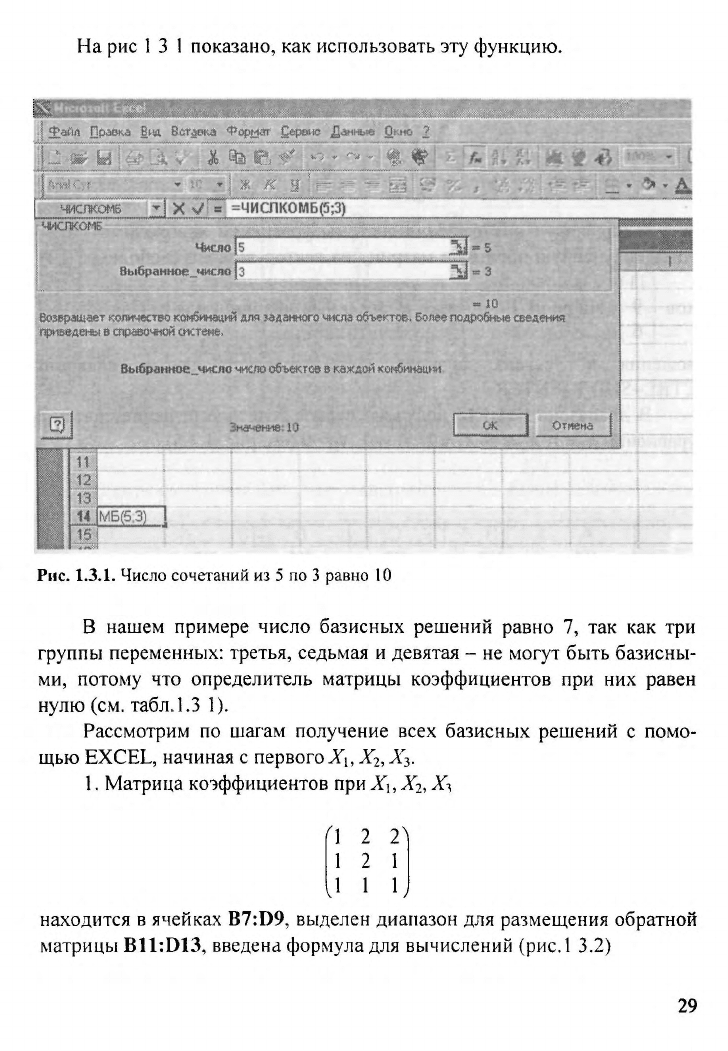
На рис
1
3
1
показано, как использовать эту функцию.
Ч
Mi
.}
£айл
Правка
1.™
Ш»
•
числксмб
ЧИСЖОМЕ
Вид Вставка
Формат Серено
Данные
1 щ
•
-
;
»j X V = =ЧИСЛК0МБ(5;3)
Число Is
Оки
0
—
щ-
ЛЧл
•4J.5
" ^ * А.
шшшшт
Вы6ранное„чисяо
[з
~3-з
=
10
Возвращает количество комбинаций для
«данного
числа
объекте»,
Более
подробные
сведения
приведены
в справочной
системе,
Вы6ранное_число
число объектов в каждой комбинации
Значение 10
Отмена
14'|МБ(5,Э)
|
Рис.
1.3.1.
Число
сочетаний
из 5 по 3
равно 10
В нашем примере число базисных решений равно 7, так как три
группы переменных: третья, седьмая и девятая - не могут быть базисны-
ми,
потому что определитель матрицы коэффициентов при них равен
нулю (см.
табл.
1.3
1).
Рассмотрим по шагам получение всех базисных решений с помо-
щью EXCEL, начиная с
первого
Х
ь
Х
2
, Х
г
.
1.
Матрица коэффициентов при Х\,
Х%,
Хт,
(\ 2 2)
1 2 1
U
1
U
находится в ячейках B7:D9, выделен диапазон для размещения обратной
матрицы B11:D13, введена формула для вычислений (рис.1 3.2)
29
