Ockendon J., Howison S., Lacey A., Movchan A. Applied Partial Differential Equations

Подождите немного. Документ загружается.

418

MISCELLANEOUS TOPICS

Fig. 9.4 Realisation of the Sine-Gordon equation.

any spatial variation but in the presence of gravity, a pendulum of length I would

respond according to the simple pendulum equation

0,0

ate+Istn0=0.

Putting these two mechanisms together, we find the famous Sine-Gordon equa-

tion184

2 !to

ate

C 8X2 - 8t2 =

sine.

(9.70)

Thus far, the only two obvious remarks that this book would have had to

say about the Sine-Gordon equation are that it is hyperbolic (we would not even

have been able to say that much about the Benjamin-Ono equation) and that

there are travelling wave solutions involving hyperbolic secants (and hyperbolic

tangents for (9.61)). The discovery that the Cauchy initial value problem can be

solved almost explicitly for the Sine-Gordon and Benjamin-Ono equations, and for

some other equations to be mentioned later, came about through a coincidence of

several seemingly unrelated trains of thought, involving conservation laws, group

transformations, eigenvalue problems, scattering theory and inverse problems; the

greatest stimulus came from numerical experiments concerning the remarkable

way in which certain travelling wave solutions, called soliton8, can `pass through'

each other and emerge unscathed, much as if they were solutions of the prototype

wave equation (9.69). Even thirty years after the pioneering work, it is still more

difficult to motivate the key ideas of soliton theory than any of the others in the

book, partly because of the absence of any elementary geometrical interpretation.

The closest we have come to soliton theory in the preceding chapters has been

in Chapter 6 when we described the possibility of using groups of transformations

to simplify certain pdes. There, we only sought simple `similarity transformations'

of the dependent and independent variables. Even the generalisation of the ideas

of §6.5 to include derivatives of the dependent variable would soon have led us into

184This equation arises in far less transparent situations than this, such as for the variation of

the order parameter in a small gap (Josephson junction) between two Type-I1 superconductors.

SOLITONS 419

unjustifiably complicated technicalities. However, there is no limit to the imagina-

tion that might be exercised when asking about objects that might be left invariant

when a pde is satisfied. Simple answers to this question that we have seen have

been that the object could be a function (e.g. a Riemann invariant) or a functional

(such as the integrated density in a conservation law). But suppose we were to ask

a question that might be posed by a scientist interested in quantum mechanics:

`could an operator that depends on an unknown function be invariant when that

function evolves according to some pde?' This is a much more recherche question

than its predecessors, as can be seen if we consider the simplest non-trivial linear

operators, namely 2 x 2 matrices. In particular, we ask `are there any odes that

a1 (t) must satisfy so that

A(t) = (a,l(t)) (9.71)

evolves in such a way that its eigenvalues and hence its invariants are constant

in time?' Not only might this be an interesting question in its own right, but it

also leads to the possibility of finding out something about the solution of the

differential equations satisfied by aid by working backwards from the eigenvalues.

Thus, suppose

Ax(t) = Ax(t),

where all the eigenvalues A are independent of t. Then there exists an invertible

matrix C(t) such that

A(t) = C-1(t)A(0)C(t).

Hence

dt, =

dt (C-') A(0)C + C-' A(0)

at-

=BA-AB,

where

B dt (C-') C = -C-'

ddC,

since C-' C = I. Note that

so that

(A - AI) (T -Bx)

(9.72)

- Bx = T(t)x

(9.73)

for some scalar function T(t). Note also that, if C were orthogonal,'85 in which

case BT = -B, then we would find from the identity

(XT X)

= XT (Bx + Tx) + (XTBT + TXT) X

181 If any of the matrices, eigenvalues or eigenvectors is complex, transpose must be replaced by

Tcomplex conjugate transpose, and C would have to be unitary, so that CC = I.

420

MISCELLANEOUS TOPICS

that, as long as Ix12 is independent of time, T(t) = 0 and the evolution of x would

be governed by

= Bx.

(9.74)

The calculation leading to (9.72) is the motivation for the famous Lax formu-

lation of soliton theory,iss which requires the generalisation of (9.72) to general

linear operators. To illustrate the finite-dimensional theory, we can construct a

system of odes for the a,3 in (9.71) by choosing any 2 x 2 matrix B whose en-

tries are functions of a;3. But we must be careful about how many of the a;3 we

allow to vary. If three were constant, from (9.72) we would obtain four odes for

the one variable entry; moreover, since the eigenvalues would only depend on this

one entry, it would have to be constant. The other extreme would be to allow

all four entries to vary and obtain four odes for them, with the constancy of the

eigenvalues ensuring the existence of two conserved quantities. It is easiest to look

at the intermediate case

all x(t) (9.75)

y(t)

a22

where alt and a22 are given constants. Then it is easy to see that, no matter what

choice we make for B, provided only that it is chosen to ensure that A is of the

form (9.75), we end up with dx/dt = F(x, y) and dy/dt = -(y/x)F(x, y), so that

xy, which determines both eigenvalues, is indeed constant.

Now let us extend this argument to the infinite-dimensional case. Suppose A is

a linear differential operator in x with coefficients that involve functions of x and

t, and again, to keep the spectrum of A constant in time, we require that

= BA - AS.

(9.76)

This is to be interpreted as saying that

WO = (BA - AB) 4i

for arbitrary smooth functions O(x, t). Now, however, we demand further that

these functions are such that (BA-AB)0 does not involve any differentiation of 0

but is purely 0 multiplied by functions involving the coefficients in A and B; hence

we will be led to one or more pdes for the coefficient functions in A and B. (This

corresponds to BA - AB being a square matrix in the finite-dimensional case; we

could not have carried through example (9.75) unless B were a 2 x 2 matrix). In

particular, for historical reasons, we could choose

A = -8x2

+ u(x, t),

so that

OAt =

'"Note the analogy between (9.72) and (9.53) and, when C is orthogonal, with the idea of

angular velocity in classical mechanics.

SOLITONS 421

and

B= -4ax3 + 3

8x + OX-U)

We would then find that (9.76) is the famous Korteweg-de Vries (KdV) equationls7

8z3

(9 77)

and equations such as (9.70) can emerge similarly when more complicated choices

are made for A.

The way is now open to construct the following intriguing recipe proposed for

the Cauchy problem for (9.77).

1. Given u(x, 0) = uo(x), find the eigenvalues of the operator A(uo) (in the KdV

case, A(uo) = -82/8x2 + uo) with suitable boundary conditions.

2. Knowing the constancy of these eigenvalues, try to find A at a later time and

from it solve an inverse problem to read off u(x, t).

This plan is much easier to state than it is to implement, because of the diffi-

culty of step 2. Hence we will restrict attention to the simplest case of the Cauchy

problem for the KdV equation with uo prescribed and positive in -oo < x < 00

and decaying sufficiently rapidly as IxI -> oo. Then u(x, t) is such that the eigen-

value problem

_8 +G

At/i =

8x2 + u(x,

t)t =

for -oo < x < oo,

(9.78)

with bounded, has a real spectrum independent of t even though A evolves

in time according to (9.76). Also, because of our assumptions about u, we expect

the spectrum to contain all negative values A = -w2, and possibly some discrete

positive values A = wn with corresponding eigenfunctions t(n) (x, t).

Now comes the key observation that this spectrum describes the modes of oscil-

lation of a one-dimensional elastic continuum modelled by the hyperbolic equation

02 Ip 02 Ip

8x2

872

in fact, setting A = -w2, 0 is related to i by

t'(x,w; t) =

tp(x, r;

dr,

(9.79)

and, by inversion, tG is a suitably weighted sum of terms t e-'"r and

Note that this is the first time in the book that we have taken a Fourier transform

with respect to a time-like variable but, in one space dimension, time and space

'"This spectacular equation can be derived from classical inviscid hydrodynamics by combining

the ideas of shallow water theory and those of modulated travelling waves (see Exercise 9.16).

422

MISCELLANEOUS TOPICS

are mathematically interchangeable. Indeed, in the following discussion we shall

at various points be thinking of both x and r as the 'time-like' variable.

We remember that we can compute the t derivatives of

and t/inl, and hence

of 10, from the generalisation of (9.73) to the infinite-dimensional case. However,

since t only enters (9.79) as a parameter, we will drop the explicit t dependence

of u,

and

' for the time being.

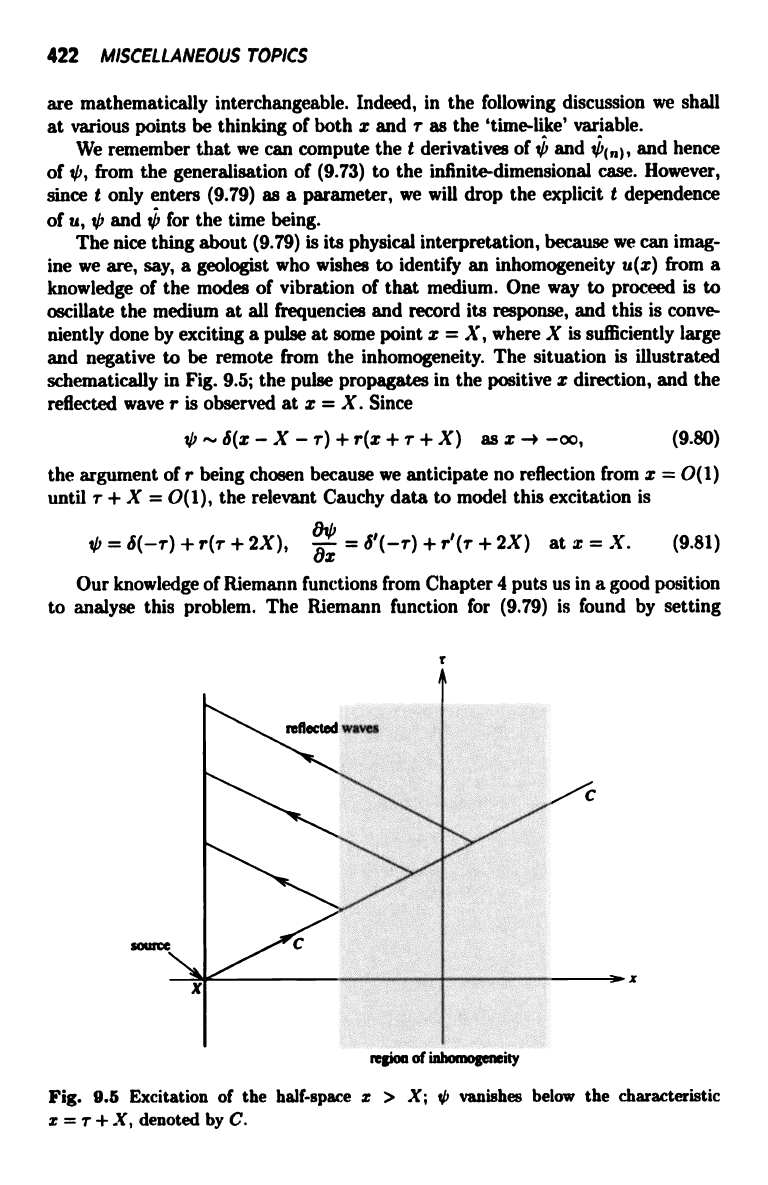
The nice thing about (9.79) is its physical interpretation, because we can imag-

ine we are, say, a geologist who wishes to identify an inhomogeneity u(x) from a

knowledge of the modes of vibration of that medium. One way to proceed is to

oscillate the medium at all frequencies and record its response, and this is conve-

niently done by exciting a pulse at some point x = X, where X is sufficiently large

and negative to be remote from the inhomogeneity. The situation is illustrated

schematically in Fig. 9.5; the pulse propagates in the positive x direction, and the

reflected wave r is observed at x = X. Since

tV-6(x-X -r)+r(x+r+X) asx-> -oo, (9.80)

the argument of r being chosen because we anticipate no reflection from x = 0(1)

until r + X = 0(1), the relevant Cauchy data to model this excitation is

0= b(-r) + r(r + 2X ),

= b'(-r) + r'(r + 2X)

at x = X. (9.81)

Our knowledge of Riemann functions from Chapter 4 puts us in a good position

to analyse this problem. The Riemann function for (9.79) is found by setting

region of inhomogeneity

Fig. 9.5 Excitation of the half-space x > X; 0 vanishes below the characteristic

x = r + X, denoted by C.

SOLITONS 423

the right-hand side equal to a product of delta functions of x and r but, from

Exercise 4.22, we could equally have considered a suitable combination of delta

functions as Cauchy data. For example, if we set vil to be the solution of (9.79)

with

zG1 = 8(-r), 8x1

= b'(-r)

at x = X, (9.82)

we find that 01 - d(x - r - X) is a bounded function of x, r and X which, for

convenience, we write as

01 -6(X-T-X) _T1(x,X,r+X),

(9.83)

where 11'1 is non-zero only in X - x < r < x - X. Now let us write = x - r and

9 = x + r, so that

02Y'1

__ 4u

(S 2 )

01;

since the 'singular support' of ?/i1 is at x = r + X, we integrate from ( = X - 0 to

= X + 0 to see that u can be retrieved from a knowledge of T 1 via the equation

lim

8P1

1 d'1'1(r+X

X,r+X) = 1u(r+X)'

(9.84)

4 I-X+o N

2 dT '

note that 'I' 1 loses its explicit dependence on X as we approach x = r + X.

Let us return to our geologist, who will find it much harder to simulate (9.82)

than (9.81). Let us therefore try to synthesise the solution with data (9.81) from

01 and 02, where

8-!1

= -d'(-r)

at x = X; (9.85)

as in (9.83), 1G2 = d(-x - r + X) + 11'2(x, X, r + X), where again W2 is bounded

and non-zero only in X - x < r < x - X. The data at x = X for the respective

Fourier transforms are

a1wX -

zy = 1 + e- r,

'1 = 1

dip

= iw(1 - e-21wXF),

dtii1

9.86)

2=1

and so = 1 + i i2e-2iwx. Hence, by the convolution theorem,

(x, T) = 01(x, r) + r (r + 2X) * 02(x, 7-)

r(T'+2X)(6(X -x-(r-r'))

+Q'2(x,X,r-r'+X))dr'

=6(x-X - T)+ 91 (x, X, r + X) + r(r + x + X)

rr+x-X

r(r'+2X)1P2(x,X,r-r'+X)dr'.

(9.87)

-Z +X

424

MISCELLANEOUS TOPICS

We need only make two final observations to turn this into an equation for 4'

terms of r.

1. The equations for ' 1 and 'P2 are

82,p1

82*1

- u(x)'Pj = 3(x - r - X)u(x),

8x2 erg

82w2

O'P2

= 5(-x - r + X)u(x) = 6(x + r - X)u(x)

( )'

8x2

u x 2

8T2

with zero Cauchy data on x = X. Hence

*1(x,X,r+X) = 92(X, X, --r + X),

so that the integral in (9.87) is

frr+x-x

( r(r'+2X)WY1(x,X,r'-r+X)dr' =

r(r"+y)'P2(x,X,r")dr",

r z+X

2X-x

say,wherey=r+Xandr"=r'-r+X.

2. By causality, r/i =- 0 in x - X > r, i.e. x > y. Hence,_when we denote the

asymptotic limit as X -* -oo of 'P 1(x, X, r + X) by 'P 1(x, r), we obtain a

linear Fredholm integral equation for W1 in terms of r:

+Y1(x,y)+r(x+y)+J r(r"+y)(x,r")dr" = 0. (9.88)

In principle, we can solve this so-called Marchenko equation for'P1 in x > y

given r, and thus retrieve u from (9.84).

The final piece in the overall jigsaw is a formula for the evolution of r as a

function of t. We remember that

1 °O

''(x,r;t) = 2-J

(x,w;t)e

1(x,t)ew"r,

°0

where, by comparison with (9.80), as x --r -oo,

(x, w; t)

eiw(x-X) +

f (w,

t)e-iw(z+X),

4 (n)(x,t) - f (n) Mew- 2,

with wn > 0, so that

roe

r(x + r, t) = 2r< f r' (w, t)e "'(=i r) dr + T(n)

(t)ew (:+r)

J 00

moreover, B - -483/8x3 as x - -oo. To study the evolution in t of i and

0(n), we must use the infinite-dimensional generalisation of (9.73) or, if we work

SOLITONS 425

with eigenfunctions whose norm is independent of t, we can use the simpler equa-

tion (9.74). Adopting the former strategy, we find that (n) can only evolve as an

acceptable eigenfunction if T (t) = 0, so that

ft(n)

while (x, w; t) must satisfy

i.e.

df(n)

-4wnr(n),

= 80 + T, V),

(9.89)

where

e-iw(x+X)

-4e-iwX (iw3Te-iws - iw3eiws) +e-iwXTw (e1' s

e'ws)

Hence,

Tw = -4iw3

and _ -8iw3f,

(9.90)

and 1'(n) and r can be found in terms of their initial values.

To recapitulate, the procedure is, given uo, to

(i) find r(n)(0), r"(w,0) and w,, as a `direct' problem in spectral theory;

(ii) update r(n) (t) and T(w, t) from (9.89) and (9.90);

(iii) solve (9.88) for 'I;

(iv) find u(x, t) from (9.84).

The terms in the solution u that correspond to the discrete spectrum wn are called

solitons (see Exercise 9.17) and they have many fascinating properties [15]. Indeed,

they are the simplest of the travelling wave solutions that we mentioned at the

beginning of this section and the inverse scattering theory explains beautifully how

they eventually emerge from arbitrary initial data and how they interact with each

other.

Putting inverse scattering theory into practice is often easier said than done,

even in simple cases. The simplest of all is when uo = u(x,0) _- 0. Then f(,,) (0) _

r' (w, 0) = 0, and so r = 0; then (9.88) gives ' 1 = 0 and (9.85) that u(x, t) =-P,

with tli = 6(x - X - r). Less trivially, suppose u(x, 0) is so small that r and W1

are also small, and the integral in (9.88) can be neglected. Also suppose there is

no discrete spectrum. We first need to find f (w, 0) in terms of uo, which we do by

writing i/i(x,w;0) = eiw(x-X) + , where

dX2

+ w2 =

uo(x)eiw(:-X)

to lowest order, with

e-i" (x+x)r"(w, 0) as x -+ -oo and proportional to eiwx

as x -+ +oo. Since, by variation of parameters,

264 = e"('-x)

uo(S) dS - e-iw(x+X) 1

u (

)e2im1 dC,

Joo

426

MISCELLANEOUS TOPICS

we find

T( 0) = uo(2w)

Now, from (9.90),

2iw

r(x + T, t) = 2x f e

siW3teiw(x+r)*(w,

0) dw,

and so

I (T + X, X, T + X) = -r(2(T + X), t) = -

2x f

2iw) dw.

!!J

Finally, reinstating the dependence of u on t,

u(r+X,t) =2d WI(T+X,X,T+X),

and so, setting 2w = k,

u(x, t) = 2a dk,

J o0

which is just the result of taking a Fourier transform in x of BU/at +83u/8x3 = 0.

This interpretation of inverse scattering theory as a generalisation of Fourier

transforms makes such a fitting end piece to our book because it illustrates how a

little basic knowledge about pdes can lead to some of the most ingenious mathe-

matical procedures ever devised for their solution.

Exercises

9.1. Suppose V2u(r, 9) = 0 in 4 < r2 < 9 and we wish to find u(2, 9) from a

knowledge of u and 8u/8r on r = 3. Show that, if

3 cos 9 - 1

6 - 10 cos 9

u(3,9)

10-6cos8' 8x(3,9) (10-6cos8)2'

then u(2,8) = (2cos9 - 1)/(5 - 4cos8).

Explain why we are lucky to have been able to do this and why we would

have been unable to find u(1/2, 9) when V2u = 0 in 1/4 < r2 < 9.

Remark. If u and 8u/8r were constant on r = 3, we could find u(R, 0) for

any R > 0. This suggests we can `regularise' the inverse problem by taking

averages of the data over r = 3, which corresponds to neglecting the high-

frequency Fourier components in u(3, 9) and 8u/8r (3, 9), thereby extending

the applicability of the Cauchy-Kowalevski theorem.

9.2. Consider a Hele-Shaw free boundary problem of the type described in Chap-

ter 7 (in three dimensions, a porous medium flow without gravity), in which,

for t > 0, fluid is injected at the origin x = 0 at a constant rate Q into an

initial domain 1)(0) containing the origin.

EXERCISES 427

(i) Setting the pressure p(x, t) = 0 outside the fluid domain 11(t), define

u(x, t) = J p(x, r) dr,t

and show that, as in §7.4.1,

10,

in fl(0)\{0},

1, in l1(t)\ft(0),

outside f2(t).

Show also that u and Vu are continuous on 8f2(0) and 80(t).

(ii) Now fix t > 0 and set O(x, t) = u(x, t) + (Qt/21r) log jxl in two dimen-

sions (O(x, t) = u(x, t) - Qt/47rlxl in three dimensions) to show that ¢

is a constant multiple of the gravitational potential due to mass of con-

stant density occupying the annular region between 011(t) and 8fl(0).

Noting that u(x, t) = 0 outside 1(t), deduce that knowledge of the

gravitational potential outside a domain, together with the assumption

of constant mass density, are not sufficient to determine the domain

uniquely.

(iii) In two dimensions, use the Green's function representation for O(z, t)

(z = x + iy and ( = f + i71) to show that, outside S2(t),

8x-iay

21r

dtd?

x-(n+t)rf

C°dCdq

8x 8 1Q(0) x - C

2tr

n.o

Jln(t)10(o)

for large IzI. Deduce from part (ii) that knowledge of all the moments

of a domain need not determine the domain uniquely.

9.3. One way to define a three-dimensional vector distribution v is by the formula

(v, t/i) = J v t/i dx,

where t, is a smooth vector test function, all of whose components vanish

rapidly at infinity. Use the formulae

where t,) and a, b are scalar and vector functions, respectively, to motivate

the three definitions

(Vv, ') = -(v, V 0)

(in which v is a scalar distribution and the inner product on the right is the

usual scalar one),

(V v, 0) = -(v, Vtii)

(in which t/i is a scalar test function), and

(V A v, b)= (v,VA0).

Show that V A (Vv) = 0 and V V. (V A v) - 0 for all scalar and vector

distributions v and v, respectively.